数学模型在高中生物复习中的情境应用——以曲线图为例

陕西

高考复习注重知识点的拓展延伸，要使各类知识点更加饱满、情境应用更加灵活多样、知识要能点对点的紧密而流畅的衔接，这就需要一定的核心思想或方法一以贯之，数学模型就是重点方法之一，使各知识点在不同情境中的运用可以达到游刃有余、形散而神聚的程度。

高中生物学作为一门自然学科，知识来源于实验和观察，数学模型自然是分析相关生物学问题的有利工具，其中，曲线图以其直观、明了、简洁的优点，呈现在对各种生命现象的分析当中，为揭示生命现象的本质特性发挥了重要作用。如物质跨膜运输的方式、影响光合与呼吸作用的因素、酶促反应、生物进化、生命活动的调节、种群的数量变化、种间关系等均会以曲线图反映相关知识，这类题型具有情境新、重能力、区分度高的特点。因此，曲线图一直是高考的重点考查方式之一。

笔者从以下三方面对常见的几种曲线类问题进行归纳，以期提高教学和复习效率。

1.速率类曲线

速率类曲线是描述过程变化的简洁数学模型，广泛地应用在与蛋白质活力有关的生命现象的情境分析中，用速率类曲线最能直观地反映相关蛋白质的活力，如以酶活性为基础的光合与呼吸速率、以载体蛋白活力为基础的跨膜运输速率等。

1.1 物质跨膜运输

这类题型借助曲线图考查跨膜运输方式的特点。首先要明确坐标含义，其次厘清曲线变化趋势及区别，最后是找到曲线与各种运输方式特征的匹配点，如此才能快速准确地判断。

【例1】图1 中曲线a、b 表示物质跨（穿）膜运输的两种方式，下列表述正确的是 （ ）

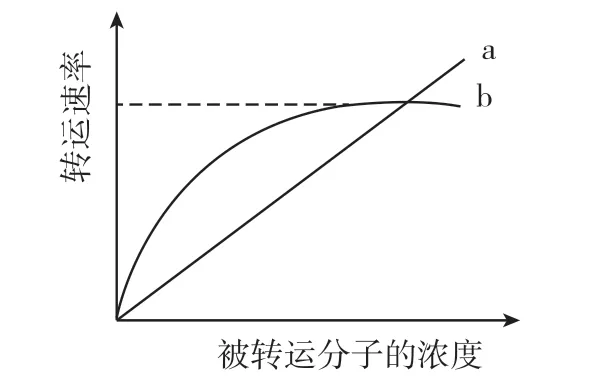
图1

A.维生素D 不能以a 方式进入小肠上皮细胞

B.与方式a 有关的载体蛋白覆盖于细胞膜表面

C.方式b 的最大转运速率与载体蛋白数量有关

D.降低细胞供氧量对a 和b 的转运速率均有影响

【答案】C

【点睛】有饱和现象为需要某种功能蛋白参与的运输方式，无饱和现象的物质跨膜运输方式是自由扩散。另外，胞吞胞吐、囊泡运输及核孔的大分子运输等均需要相关功能蛋白参与，也会出现饱和现象。

1.2 酶

考查“酶”相关考点的试题多以坐标曲线图为背景，主要考查温度等条件对酶活性的影响及学生对图文知识转化的综合能力，常以分析曲线变化原因及对策的题型为主，深度考查时会涉及竞争性抑制和非竞争性抑制曲线及原理，除此之外个别曲线会另辟蹊径考查酶的本质。

【例2】图2 表示酶活性与温度的关系。下列叙述正确的是 （ ）

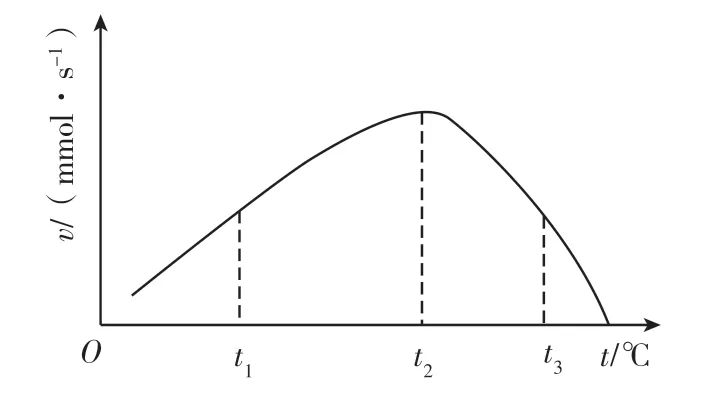
图2

A.当温度为t2时，该反应的活化能最高

B.当反应物浓度提高时，t2对应的数值可能会增加

C.温度在t2时比在t1时更适合酶的保存

D.酶的空间结构在t1时比t3时破坏更严重

【答案】B

【点睛】酶的最适温度绝对不是某一固定值，而是受特定的酶促反应条件影响的，如底物浓度、pH 等。酶具有最适温度是所有酶的固有属性没错，但绝不可把这一数值固定化。

1.3 光合作用和呼吸作用

光合作用和呼吸作用的曲线可以单独考查，也可以综合在一起考查，后者只是情境复杂了些，需要厘清两者的逻辑关系，通过仔细分析，以某种物质的量变表示出来即可。由于不论是呼吸作用还是光合作用，基本上都是以分析细胞及以上生命系统层次的生物材料为对象，所以务必分析清楚不同条件对两种代谢过程的影响大小，这样才能做出正确判断。

【例3】（原创）图3 为某一植物在不同实验条件下测得的净光合速率，下列叙述分析错误的是 （ ）

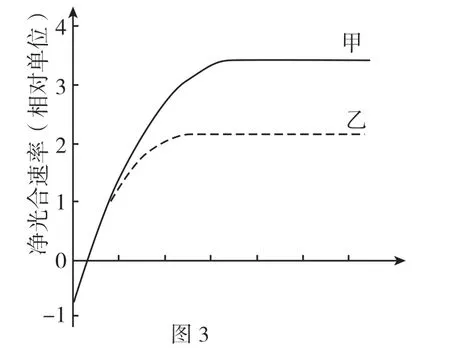
A.曲线起点为负值，表示植物进行呼吸作用不进行光合作用

B.若横坐标是温度，甲、乙曲线早期重合可能是实验的无关变量不适宜导致

C.若横坐标是光照强度，甲表示适宜温度，乙表示较低温度

D.若该植物的净光合速率为零，其叶片和根的净光合速率却不为零

【答案】B

【点睛】光合速率曲线分析时应重点关注起点、交点、饱和点及其之间的数量关系，而这些问题的准确解答又必须建立在曲线形成原因的细胞水平上的分析，因此，光合速率复习时，曲线分析必须结合细胞模型图。另外，多曲线的分析要遵循实验单一变量及无关变量适宜且相同原则。

2.相对数量类曲线

如果研究重点是生命现象的状态量变化，相对数量曲线则更为直观，这类题型主要集中在类似酶促反应类问题（包括酶促反应、光合作用与呼吸作用）、渗透作用（原生质体体积变化或者细胞液浓度变化）、进化的实质（基因频率变化）、生命活动调节（激素变化、电位变化）及种群数量变化问题（增长曲线等）等方面。相对数量曲线要比速率曲线简单一些，抓住始末点、拐点、斜率等信息基本就能对相关生命现象做出科学合理的分析，下面选择上述相对数量曲线中，几种最为常见的曲线图示例进行分析。

2.1 酶促反应类（光合作用与呼吸作用）

酶促反应类的相对数量曲线除可以考查相关物质的量变，也可考查该曲线的导函数曲线——速率问题，分析时须注意两个量的对应关系，进行合理转换，即可正确作答。

【例4】（2018 年，天津卷，第5 题）为探究酵母菌的呼吸方式，在连通CO2和O2传感器的100 mL 锥形瓶中，加入40 mL 活化酵母菌和60 mL 葡萄糖培养液，密封后在最适温度下培养。培养液中O2和CO2相对含量变化如图4。有关分析错误的是 （ ）

图4

A t1→t2，酵母菌的有氧呼吸速率不断下降

B.t3时，培养液中葡萄糖的消耗速率比t1时快

C.若降低10℃培养，O2相对含量达到稳定所需时间会缩短

D.实验后的培养液滤液加入适量酸性重铬酸钾溶液后变成灰绿色

【答案】C

【点睛】酶促反应速率若以相关物质的相对含量表示，需要关注曲线斜率变化。

2.2 生命活动调节

有关调节部分的曲线模型集中在动作电位及协同（拮抗）关系等方面，主要以调控机理、过程变化、曲线斜率、极值比较、实验分析与设计等为主，难度逐渐加深，综合性试题都具有明显的进阶性问题设置，注重科学思维和科学探究等能力的考查。

【例5】（2018 年，江苏卷，第11 题）图5 是某神经纤维动作电位的模式图，下列叙述正确的是 （ ）

图5

A.K+的大量内流是神经纤维形成静息电位的主要原因

B.bc 段Na+大量内流，需要载体蛋白的协助，并消耗能量

C.cd 段Na+通道多处于关闭状态，K+通道多处于开放状态

D.动作电位大小随有效刺激的增强而不断加大

【答案】C

【点睛】动作电位及静息电位主要与细胞内外的K+和Na+有关，也会受其他带电粒子影响，如Cl-等，但不是主要原因，在表述时需要注意。一次动作电位造成的K+和Na+移动量相对整个细胞内外K+和Na+总量来说极其微小，既不会改变K+和Na+的内外分布，也不会改变K+和Na+的跨膜方式。另外，个别题型另辟蹊径，横坐标是距刺激点的距离，此类图形形成的生理过程正好与该图相反，需要注意。总之，复习教学中，教师需要把所学模型讲清、讲透，在具体的情境应用中厘清概念，适当转换思路，做到灵活运用。

图6

2.3 种群数量变化

此类曲线模型是最典型的数学模型的建模与应用范例，模型曲线的产生情境、建模思想、数学表达式及对应曲线、二阶曲线的对应关系等是考查的高频考点，应充分理解模型曲线产生的情境及数学表达式，运用逻辑思维，正反向演绎推理可得正确结果。

【例6】（原创）研究团队对某一自然水域中的鳜鱼种群进行了持续研究，得到了以下数据，相关分析不正确的是 （ ）

A.有害动物及有益动物的种群数量都应控制在K/2为佳

B.出生率和死亡率是影响鱼群种群密度变化的直接原因

C.平均增长量、净补充量及种群增长率出现最大值的时间不同

D.鱼个体平均增长量与鱼群数量呈反比是由于生存压力逐渐增大

【答案】A

【点睛】“S”型曲线形成的最终原因是环境资源有限，可以有多种表示方式，如个体的平均增长量、个体食物或者空间获取量、种群增长率、净补充量等，虽然形式多样，情境却是一样，分析时要抓住本质。

2.4 群落与生态系统

群落与生态系统中的相关曲线基本以反映种间关系为主的逻辑性曲线为主，没有固定模型，曲线形式变化较多，但都具有可依托的明显可辩的逻辑理论，如捕食关系、竞争关系、动植物物种多样性之间的关系、物种丰富度与演替的关系、物种多样性与稳定性的关系、收割理论与物种多样性关系等，理解清楚这些基本的生物学逻辑关系之后此类型曲线分析对学生来说都属于较为简单的问题。

【例7】（2017 年，天津卷，第7 题节选）大兴安岭某林区发生中度火烧后，植被演替过程如图7。

图7

据图回答：

（2）火烧15 年后，草本、灌木丰富度的变化趋势均为________________________________________________________________________。

（4）用样方法调查群落前，需通过逐步扩大面积统计物种数绘制“种 -面积”曲线，作为选取样方面积的依据。如图8 是该林区草本、灌木、乔木的相应曲线。据图分析，调查乔木应选取的最小样方面积是________________________。

图8

【答案】（2）下降后保持相对稳定（4）S3

【点睛】群落演替的动力来自生存斗争，其中优势种是演替的主角，获取资源能量更强的物种依次崛起，优势种不断易主，但后一优势种不是完全替代前一优势种，只是在数量和空间分布上占据绝对优势，这也是随着演替进展物种丰富度不断增大的原因。当然，演替方向也是相对的，如退化的演替——荒漠化等，物种丰富度则不断降低，甚至消亡。在用样方法调查植物丰富度的时候，应考虑不同植物的分布情况，选择能够包含该类植物所有种类的最小样方为佳。

3.曲线模型的构建与应用

3.1 模型曲线的应用

综合模型曲线主要是各种具有相似变化规律曲线的求同思想产物，除了理解相同曲线背后的不同原理之外，更重要的是培养学生归纳概括的高阶理性思维能力，有大道至简这样的理性思维，更应该理解生命现象中的变化与稳态思想。

【例8】（原创）下列四种现象中，可以用图9 表示的是 （ ）

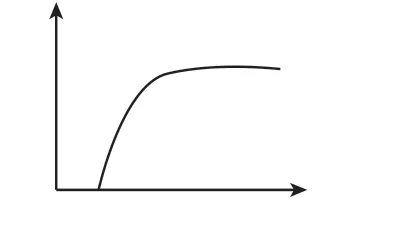
图9

A.在适宜条件下光合作用强度随CO2含量的变化

B.条件适宜、底物充足时反应速率随酶浓度的变化

C.一个细胞周期中一条染色体DNA 含量随时间的变化

D.某种入侵生物在理想条件下种群数量随时间的变化

【答案】A

【点睛】本题主要考查相关生理过程中的数量变化趋势，既有微观的细胞代谢，也有宏观的种群变化，需要较强的获取信息和情境应用能力。学生需要注意曲线的起点、斜率、饱和点等，依据相关变化特征，对应正确的曲线模型。

3.2 新情境下曲线的构建与分析

【例9】某研究团队对新研发成功的转基因玉米光合速率进行了相关检测，获得数据如下，叶片净光合速率（Pn，以CO2吸收速率表示）与胞间CO2浓度（Ci）的日变化曲线如图10，叶面积系数（单位土地面积上的叶面积总和）与植物群体光合速率、呼吸速率及干物质积累速率之间的关系如图11。请分析回答：

图10

（1）据图可知，与11:00 时相比，13:00 时叶绿体中合成C3的速率___________；Ci 的日变化曲线主要受__________影响。

（2）由图11 分析可知，植物群体光合速率、呼吸速率及干物质积累速率之间的关系可表示为____________。

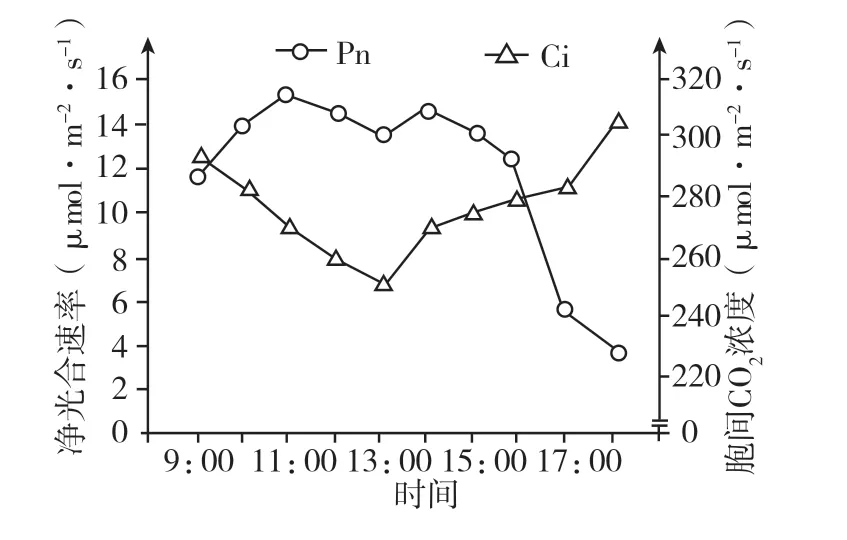
图11

（3）结合图10 和图11，在其他条件适宜且相同情况下，当叶面积系数分别在a、b 两点时，分析叶片相应的Pn 值大小关系。

【答案】（1）更快 光照强度（2）植物群体光合速率=呼吸速率+干物质积累速率（3）叶面积系数为a 时，净光合速率最大，比叶面积系数为b 时的净光合速率更高，而Pn 值可直接反映净光合速率大小，故叶面积系数a 点时的Pn 值大于b 点对应值。

【点睛】新情境下曲线的构建与分析主要从两个方面推陈出新：一是曲线图的形式新，如新概念对应的多曲线共同出现；二是分析对象新，如选用生命系统不同层次的实验材料。这些表面新颖的情境考查的生物学原理及分析方法却都是一样的，找准模型与方法，合理分析即可。

综上，数学模型在生物学乃至其他理科学科的应用，均是一种分析表面现象的工具，通过分析某一生理过程中相关物质的数量变化以反映该过程，归纳为两种方法：过程量分析和状态量分析，常以速率和相对含量表示，表面上来看，两者不同，究其数学本质而言，只是导函数与函数的关系，实际反映的是同一过程的不同方法。师生要做的就是厘清试题所给的新情境，鞭辟入里，理性思考，找准对应的数学模型，即可准确而高效地分析应用。