改进滑模极值搜索控制在阻抗匹配的应用
2021-05-29李颖晖武颂尧邱枭楠
李颖晖, 武颂尧, 林 茂, 邱枭楠, 李 勐
(1.空军工程大学航空工程学院,西安,710038;2. 国防科技大学军事职业教育技术服务中心,长沙,410037)
等离子体隐身技术是一种主动反雷达隐身技术,依靠自身特殊的物理性质以及对电磁波的特殊作用来达到隐身目的[1-4]。等离子体放电一般使用大功率射频电源。目前已有使用13.56 MHz射频电源应用于电磁散射方面的研究[5-7],但存在电源体积较大的缺点且电源效率较低,不适于在飞行器的应用。因此,需要通过合理的小型化等离子体放电电源设计,在提高电源效率不增加飞机总功率负荷的基础上,有效降低其RCS。针对小型化高效率的设计要求,本文通过优化设计射频电源阻抗匹配控制方法提高电源效率。
张春雷首次利用极值寻优控制(extreme seeking control, ESC)对射频等离子体阻抗进行实时匹配,大大加快了等离子体负载的匹配速度提高耦合功率[8]。为提高ESC的控制性能许多人对其展开了研究,殷春等人利用分数阶微积分方法,改进SM-ESC提出了一种分数阶算法FO-SMESC,该方法有效的提高系统的快速性和鲁棒性但控制方法较为复杂[9]。文献[10]采用模糊规则优化分数阶的控制作用,减小了算法的稳态震荡。此外,极值搜索算法可以与其他控制方法进行结合,达到控制参数优化的效果。文献[11]提出一种嵌入粒子群优化算法优化SMESC的控制参数,提高了追踪精度,降低功率损失,但是忽略了随机扰动的影响。文献[12]通过构造SMESC的目标函数,并使用时间加权绝对误差IIWO优化算法对积分增益和增长率进行在线优化,降低稳态振荡和收敛时间,但是该方法在减小系统稳态幅值的同时算法的复杂度较高。
本文使用另一种较为简单的终端滑模的方法对SMESC进行改进。针对传统SM-ESC在快速寻优的同时引入较大的稳态振荡的缺点,结合终端滑模方法提出改进的快速终端滑模极值搜索控制。在保证系统的稳态振荡幅值减小的条件下,同时提高了收敛速度,并且在一定程度上减小了系统计算的复杂度。为等离子体隐身电源小型化提供了一种新的优化设计方法。
1 阻抗匹配
射频等离子源一般由信号源、功率放大器、匹配网络三部分构成。匹配网络的作用为阻抗变换即将给定阻抗变换为需要的阻抗,实现最大功率传输。由传输线理论,源功率减去反射功率即为负载功率Pl=Pf-Pr。负载功率Pl计算公式为:
(1)
式中:Vs和Vl为源电压和负载电压Zs=Rs+jXs;和Zl=Rl+jXl为源阻抗和负载阻抗。阻抗正配原理见图1。
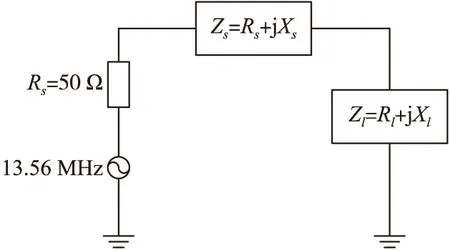
图1 阻抗匹配原理框图
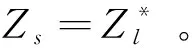
在这种情况下,Pr=0,传输效率最高。匹配电容C与负载功率Pl的关系为:
Pl=h(C)
(2)
式中:h(C)即为ESC的性能指标函数[14]。
由于在实际系统中存在各种外界的未知干扰,同时,在特定放电条件下,Pl为关于匹配电容的单峰极值函数。因此,一种不依赖精确模型描述的无模型控制器ESC非常适合应用于阻抗匹配控制。ESC控制下的阻抗匹配控制原理见图2。
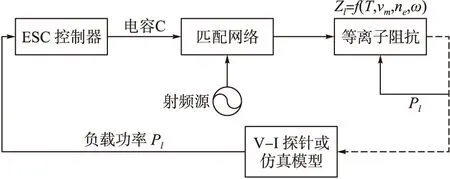
图2 阻抗匹配控制原理
2 快速终端滑模极值搜索
阻抗匹配控制为确定匹配网络可调元件值,将射频功率传输到最大功率点,由第1节分析可知,负载功率Pl为极值函数,以L型匹配网络的并联电容值为控制输入u,负载功率为系统的输出y。滑模极值搜索算法的控制结构如图3所示。
图3中,k、β、ρ为控制参数。系统的滑动变量δ(t)为:

图3 滑模极值搜索控制结构
δ(t)=P(t)-g(t)
(3)
式中:g(t)=ρt。对滑动变量δ(t)进行求导可以得到:
(4)
式中:φ(u)为输出有功功率;H(u)对输入可变电容u的偏导数;sgn()为符号函数。
输入参数u定义为:
(5)
2.1 滑模极值搜索
由SM-ESC的原理可知,极值搜索过程分为3个阶段。
1)收敛阶段,从系统初值收敛到滑模态;
2)滑动阶段,在滑模面上做滑模运动,收敛至极值点;
3)稳态振荡阶段,脱离滑模面在极值点附近稳态震荡;
进入稳态振荡时|φ(u)|<ρ/k,滑模态消失。
(6)

1)ρ/k较小时,当系统进入滑模面δ(t)=(2n-1)β之前,会穿越区域|φ(u)|≤ρ/k,并再次进入|φ(u)|>ρ/k区域,达到收敛条件。在滑模面δ(t)=(2n-1)β上运动并向|φ(u)|≤ρ/k收敛。进入区域|φ(u)|≤ρ/k前同样会得到:
(7)
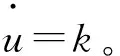
滑模信号δ的变化情况如图4所示。系统首先从初始状态收敛到滑模面,然后在滑模面上做滑模运动,在脱离滑模面后δ逐渐减小,并经过不同的滑模面,形成稳态振荡。

图4 滑模信号δ变化曲线
由SM-ESC原理可知,在收敛阶段,需要较大的k和较小的β使系统尽快达到滑模面。在滑动段需要较快的收敛速度,需要较大的ρ,由式(6)可得滑动段的滑动范围于与ρ/k相关,在稳态振荡阶段,振荡幅值kβ/ρ正相关。
2.2 切换无稳态振荡极值搜索
基于2.1节中分析结果,在收敛的第3个阶段系统存在稳态振荡且与前两个阶段的参数相互影响,提高系统的快速性就会增大稳态振荡,减小稳态振荡就会使系统搜索速度减小。这种特点限制了滑模极值搜索算法的应用。在本节提出了一种基于切换的SM-ESC方法,利用设定的切换函数在稳态阶段加入终端滑模面,在不同搜索阶段自适应改变滑动参数的变化率,在保证快速收敛同时减小稳态振荡幅值,克服基于传统SM-ESC的缺点。
2.2.1 终端滑模控制
线性滑模(LSM)与终端滑模(terminal slid mode,TSM)的关系表达式为:
(8)
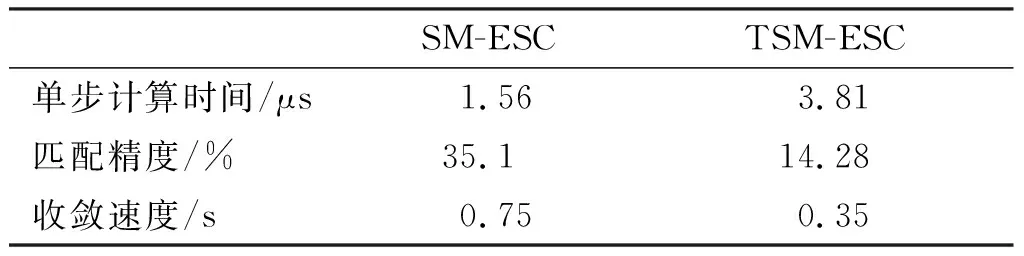
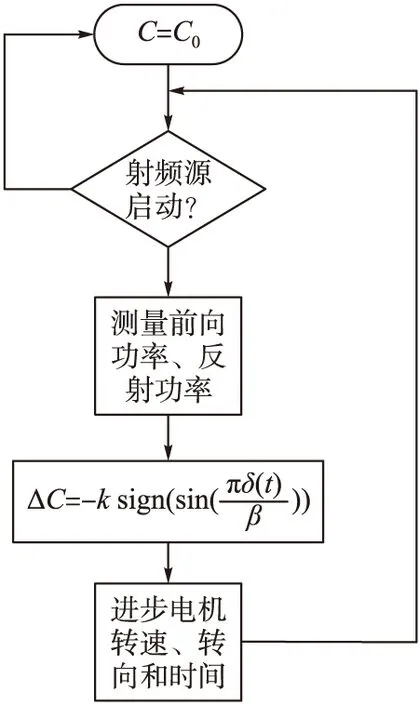
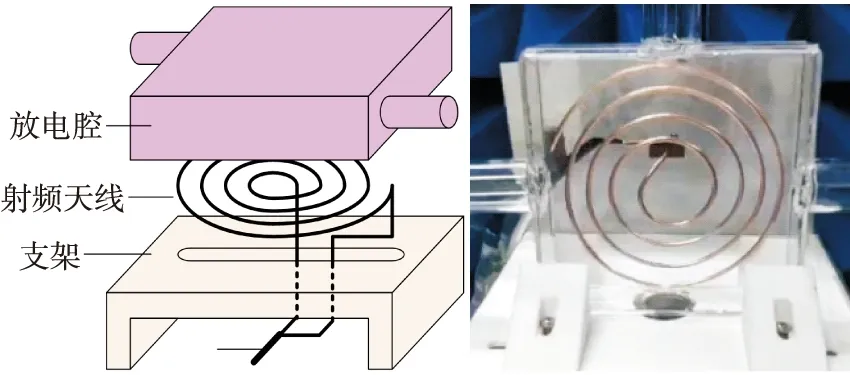
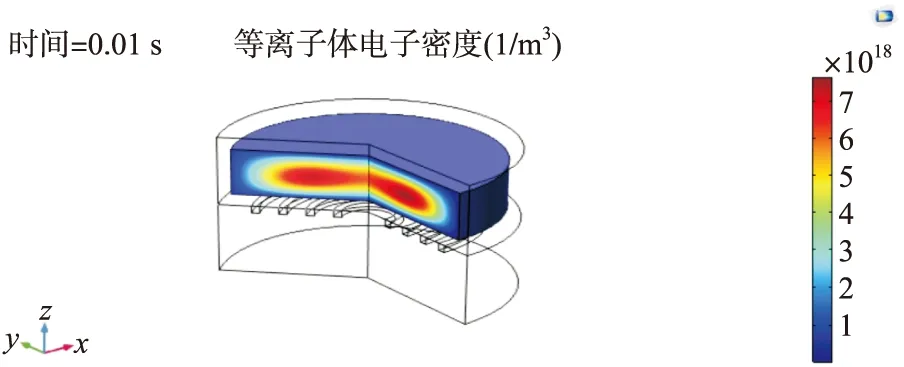
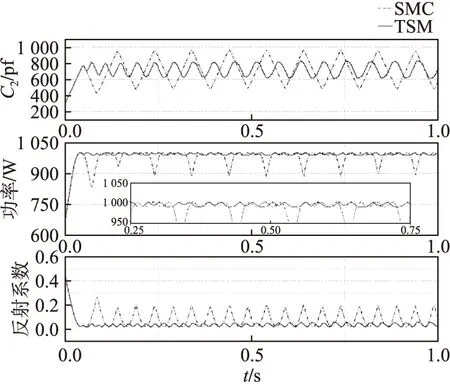
式中:s∈R为系统状态;1/2 终端滑模面的设计解决了系统不能在有限时间内收敛到零的问题。其通过加入非线性部分,提高了向平衡状态靠近时的速度,且由于1/2 图5 不同滑模面系统状态和收敛速度 由图5可得,当s>1时,LSM的收敛速度快;当s<1时,TSM的收敛速度快。 由2.1节可知系统进入稳态阶段后,以极值点左侧为例,(2n-1)β 由滑模收敛过程的分析可以得出对任意初始值P0,都会收敛于滑模面s=[y0/β]和s=[y0/β] ±β,且当滑模状态从二阶段进入三阶段后,s发生了明显变化。因此,可以利用信号s(t)来区分基于滑动模式的ESC的收敛阶段。 选择在滑模过程结束时为切换时刻,[y0/β] ±3β作为切换阈值。系统切换控制律设计为: (9) 式中:[·]表示·的取整函数。 式(9)决定了滑模收敛过程中的切换时刻,在γ为0时,滑模极值搜索工作完成滑模搜索的第1、2阶段,当γ为1时,进入无稳态振荡的终端滑模控制过程。基于切换的终端滑模极值搜索控制结构见图6。 图6 切换滑模极值搜索控制结构 2.2.2 稳定性分析 由2.2.1节,通过对s/β取余数可以将稳态振荡环节的每一阶段转化到(0,1)之间。由图5所示的系统相图可知,在系统变量处于(0,1)之间时终端滑模面的收敛速度最快。 (10) (11) 在Intel(R) Core(TM) i7-4690 CUP、主频3.6 GHz、8 GB内存的台式机上对快速终端滑模极值搜索控制算法和传统SM-ESC算法进行相同工况的阻抗匹配仿真计算,计算效率结果见表1。 表1 不同算法计算效率 通过对比,TSM控制相对于传统SM-ESC算法增加了一定的计算复杂性,但有效提高了对于匹配电容值搜索算法的收敛速度同时降低了系统的稳态振荡提高收敛精度。 阻抗匹配控制系统硬件平台由个人PC、驱动电路、电机控制器,射频电源组成如图7所示。利用个人PC上的MATLAB/Simulink平台搭建整个控制系统模型。计算机通过仿真器与DSP连接,模型执行文件通过JTAG链接下载到DSP中。射频功率由匹配器转移到负载ICP中。由双向耦合器采集到的前向功率与反射功率,经低通滤波器模数变换输入到DSP控制器中,完成系统输入并执行所有的控制,如模拟信号采样,无刷直流电机电子换向,PWM产生和SMC算法等。DSP输出的控制信号经驱动电路与步进电机连接控制匹配电容。 图7 控制系统模型 图8显示了控制器的简要流程图。启动射频源,通过双向耦合器测量负载端与匹配器的前向功率Pr和反射功率Pf。基于前向功率Pr的测量值,根据式(12)改变匹配电容C。进一步根据电机位置与电容的关系改变步进电机的转速和转向。经过反复迭代,匹配电容和前向功率Pr向目标最大功率点位置变化,并在极值点附近做振荡。 图8 控制器流程图 (12) 以L型阻抗匹配网络为例,仿真了电感耦合等离子体的阻抗匹配过程。仿真原型为平面螺旋型的线圈射频天线,如图9所示。 图9 腔体与放电线圈 系统的几何特征如下:放电线圈采用1 mm铜线绕制而成,线圈共绕4圈,每圈间距9 mm。射频电源频率为13.56 MHz,电源内阻50 Ω。RF功率为1 000 W。本文通过COMSOL Multiphysics软件对透波腔的阻抗模型进行计算。仿真模型如图10所示。 图10 等离子体的腔室COMSOL仿真模型 经过仿真与实验验证,在T=300 K,P=30 Pa条件下等离子阻抗为Z=4.829+67.711j,由史密斯圆图可得该条件下的网络匹配电路值为C1=221.7 pf,C2=718 pf。选择控制参数ρ=20,k=10 000,β=1。系统初值为u0=300。对本文所提算法与SM-ESC的仿真结果对比如图11所示。 图11 TSM与SMC仿真对比 为了更好地说明本文所提算法的性能,图中不仅给出了输入匹配电容C2的变化情况,同时给出了反射系数和输出负载端有功功率的变化图。由图中局部放大图可知在收敛速度相同的情况下,传统滑模方法负载端有功功率稳态振荡约为100 W,而所提出的滑模极值搜索控制方法的稳态振荡很小。 由于在实际放电过程中,(E-H)模式跳变以及放电条件的变化对激励器负载特性有较大影响。为进一步分析系统的动态收敛性能,证明该方法在保持较快收敛速度的同时减小系统稳态振荡。本文考虑了负载突变对系统控制效果的影响,对传统SMC在兼顾收敛速度和稳态振荡的情况下。经过实验,选择最优控制参数ρ=15,k=2 000,β=1。同时对TSM选择控制参数ρ=20,k=3 000,β=1。系统初值均为u0=300,且在2 s将射频功率由750 W变为1 000 W,匹配网络匹配电容C2的动态响应如图12。 图12 C2的动态响应 图12给出了在2 s时刻,输入功率变化时,匹配电容C2的变化。从图13中可以看出,TSM控制方法可以快速的在0.1 s内(如图A点)找到系统匹配电容值672 pf,得到射频源的最大功率输出点,而SMC则需要1 s(如图B点)才可以收敛。在2 s时刻由于输入功率变化,负载阻抗发生变化,系统同样在较短时间内找到1 000 W下的匹配电容值718 pf,同时,从局部放大图可知系统的稳态振荡也得到了改善。通过在稳态条件下测量不同功率下负载阻抗,由史密斯圆图可知匹配电容值较为准确性。 在射频放电中,由于功率变化,线圈会从E模式跳变至H模式,导致激励器阻抗变化范围较大,而自动匹配器所匹配的电容不仅匹配所需时间长,且在变化范围较大时需要手动调节,不能满足匹配要求。因此本文将所提算法引入到自动匹配器的匹配电容计算中,通过测得的反射功率自动寻优当前条件下的匹配电容,并调节电容C2。实验中对平面螺旋型感应耦合等离子体激励器进行放电实验,负载在不同功率下放电图像如图13所示。 图13 放电图像 图13中,(a)为放电开始时,(b)为100 W时E-H模式转变放电图,(c)为使用双可变电容匹配时由自动匹配器匹配750 W放电图,(d)为使用SMC调节匹配器的匹配电容时750 W放电图,(e)为使用TSM调节匹配器的匹配电容时750 W放电图。通过观察750 W时射频源显示的反射功率值,双电容自动匹配器不仅需要提前手动调节且匹配时间较长,反射功率维持在67 W左右,使用单电容SMC算法反射功率维持在65 W左右匹配时间缩短,而使用单电容TSM优化算法可以将反射功率调至50 W左右。从实验结果来看该算法对于反射功率的降低起到了一定的效果。 另外分析放电后的图像形状,实验结果与文献[18]结论相同:外电路阻抗会影响放电区域电子密度分布。从图可知,TSM优化后放电更加均匀,线圈中部的耦合效果更佳,发光更亮。对于透波腔的电磁散射效果更优。综上,TSM方法可有效提高收敛速度减小电路功率损耗,同时在保证速度的情况下对系统稳态振荡的消除较为明显。 本文以透波腔ICP为研究对象,设计了一种改进滑模极值搜索的阻抗匹配控制方法。通过仿真和实验验证了该新型控制方法的有效性。得出了如下结果: 1)为提高ICP射频源阻抗匹配网络的匹配速度和匹配精度,本文提出了一种SMESC与终端滑模相结合的控制策略。 2)理论分析表明,本文控制策略可以保证系统在减小SMESC在稳态阶段振荡同时提高收敛环节速度。 3)仿真和实验结果表明,相比于SMESC控制,本文所提出的控制策略TSM在保证收敛速度的同时提高了匹配精度,进而减小电路功率损耗,提高电源效率,并且改善了透波腔的密度分布。因此,TSM对于减小功率损耗,能在保证快速达到匹配阻抗的同时抑制稳态阶段振荡,并且改善了透波腔的电子密度分布。


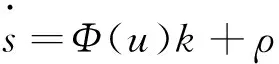
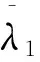

3 实验验证



4 结论
