内涵与外延之辩：基于含糊性语义解释演进的分析

张立英 张君

1 引言

含糊性（vagueness）问题通常由含糊表达所引起。含糊表达在自然语言中随处可见，例如高、矮、贵、秃头、聪明等等。含糊表达最核心的特点在于，存在一些边界例子，我们不好判断这些例子是否满足含糊表达的性质。例如，如果刘云不是高到明显高，也不是矮到明显矮，则他是高或矮的边界例子。同时，含糊表达会导致累积悖论。如，对于含糊词秃头，已知0 根头发的人是秃头；如果有n根头发的是秃头，则有n+1 根头发的是秃头。……由此一直推下去，我们甚至可推出：有100,000 根头发的是秃头。该论证看起来是有效的，前提看起来也都为真，但结论却不为我们所接受。1累积悖论（sorites paradoxes），又称沙堆悖论、秃头悖论，最早由欧布里德（Eubulide）提出，在标准的古希腊语中，sōritēs 的意思是heap。在含糊性问题研究领域，研究者们试图从新的视角重新诠释这一悖论。一个完整的含糊性问题的解释理论需要给出含糊句的真条件，同时给累积悖论现象以合理的解释。

为了解释边界例子，一种很自然的想法是引入真、假之外的不定值，于是，三值逻辑被用来解释含糊性。但这种处理很快就遇到了问题。例如，对于粉和红、小和大之间的液滴，我们会认为该液滴是粉色的且是红色的为假而该液滴是粉色的且是小的真值不定；但由于这两句话的支命题都是不定值，如果将这两句话写成真值运算的形式则有：∧(不定,不定)=假，∧(不定,不定)=不定2这里用“∧(,)”表示与语句中“且”对应的真值函数，范启德（K.Fine）3范启德（姓名），一译为范恩（姓）。本文中，K.Fine 和K.Akiba 等的翻译规则保持一致，都采取全名翻译。就此还进一步提出了半影联系（penumbral connection，[5]，第270 页）的概念，即真值关系在不定值之间仍旧得以保持的可能性，例如，即使是处于大和小之间不定状态的液滴，该液滴小且并非该液滴小仍旧应该为假。经典三值逻辑4这里的经典三值逻辑指的是卢卡希维茨（J.Łukasiewicz），克利尼（S.C.Kleene）等所给出的三值逻辑，尽管他们给自给出的三值赋值函数是有差异的，但都可以列出真值表，本质上都是真值函数。中的真值运算无法刻画出这种更细致的区分。

模糊逻辑（fuzzy logic）也被用来解释含糊性问题。模糊逻辑在完美真（1）和完美假（0）之间引入了无穷多的真值，又被称作真值度理论或者概率解释。边界例子正介于0 和1 之间，例如：作为边界例子的刘云高其真值可能取0.68。由于可以通过赋值的不断微调来体现出渐进式的变化，模糊逻辑对累积悖论的解释看起来更加自然。5模糊逻辑对累积悖论的处理比较直观：以秃头为例，如果只有真假二值，我们说100000 根头发的人是秃头为假，有0 根头发的人是秃头为真是没有问题的，但一定存在0 和100000 之间的某个m，使得m 根头发的人是秃头为真，而m+1 根头发的人是秃头为假，这样突兀的边界从人类认知的角度看起来十分不自然；模糊逻辑提供的解释下，因[0,1]区间里可以有[0,0.00001,0.00002,…,0.99999,1]这样的赋值，就会让这种过渡看起来自然一些。但模糊逻辑本质上仍是线序6线序，又叫全序，本文后面与之相比较进行讨论的还有偏序。线序和偏序都是集合论概念。线序关系满足反对称性，传递性和完全性；偏序关系满足自反性，反对称性和传递性。线序的直观是集合内任何一对元素在在这个关系下都是相互可比较的；偏序关系则允许集合中的元素不可比较。线序是一种特殊的偏序。模糊逻辑语义下的无穷个真值组成的集合中每个元素都可以比较大小，因而是线序。的真值函数，其特点在于：每个真值赋值之间都可以比较大小，同时联结词都是关于真值的函数，可以进行真值运算。在这种解释下，经典三值逻辑中所遇到的真值运算带来的问题仍旧存在，例如，在模糊逻辑下，如果李琳高的真值为0.5，则李琳不高的值也为0.5，所以，李琳高且李琳不高的值也为0.5。但直观上，后面这句话的应取值为0。除此之外，由于模糊逻辑是线序的，每个赋值之间都可以比较大小，无法解释多维含糊性问题。例如，对于模糊表达聪明，因为存在多维度的聪明，比如记忆力好、反应敏捷、理解力强、综合分析能力强等等，因此我们不可能把主体按照聪明程度按赋值数字的大小简单排成一个线序；类似的，秃头、美等等也都具有多维含糊性。

2 含糊性问题的可精确化结构

同样想解释含糊性，范启德引入了精确化（precisification）这一概念。他认为，在真与假之间存在真值间隙（truth gap）7真值间隙（true gap），由范弗拉森(B.C.Van Fraassen，[6]）提出。，而边界例子正是真值间隙的例子，他们既不真也不假。但这种“不定”可以有很多不同的方式最终变精确。

以语句小赵是秃头为例，假设小赵是秃头的边界例子，这句话看起来没有真值，但范启德认为，人们之所以认为在现实世界（不妨设为@）中这句话没有确定的为真或为假的真值（因此为不定），是因为同时存在现实世界@ 的精确化（precisfication）8精确化可看作模态逻辑中的可能世界。b和c，在b中，小赵是秃头为真，在c中，小赵是秃头为假。范启德还认为，在现实世界@中已经确定为真（假）的语句，在其精确化中仍旧保持为真（假）。在这一理论下：现实世界@本身也是自己的一个精确化，如果一个世界的精确化中包含了在原世界中不定但在其精确化中变为真（假）的语句，则该世界为原世界的真精确化。基于这一分析，我们可以构建出关于精确化的空间结构，这里称之为可精确化空间9范启德将之称为规范空间进路（Specification Space approach），秋叶研将之称为模态精确化进路（Modal-Precisificational Approach）。本文作者称之为“可精确化”，是因为这样可以凸显这一理论预设了“可精确化”。。由于各精确化之间的关系是偏序，因此这样的可精确化空间是偏序空间。举例明之：

假设昆家寨（K）是一个存在于精确区域A、B、C附近的模糊区域，它们之间的关系如下：C ⊆A（即C包含在A中），C ⊆B，A⊈B，和B⊈A（见图1）10此例来源于秋叶研（[1]），有修改。。

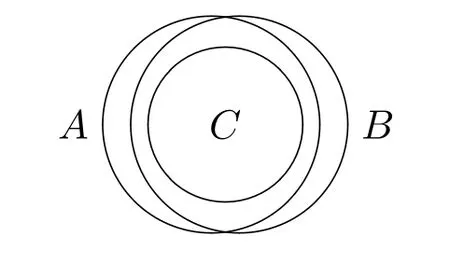
图1:昆家寨（K）

在现实世界@中，K的边界是模糊的，不确定是否有A ⊆K，B ⊆K或者C ⊆K，这意味着，对于“是否包含于K”这件事，A、B、C都是边界例子。于是，对于A，存在一个现实世界@的精确化b，在b中A ⊆K，同时存在@的另一个精确化c，在c中A⊈K。已知C ⊆A，因此，在精确化b中也有C ⊆K。对于b和c，分别有两个更进一步的精确化d和e，f和g，在其中B ⊆K或者B⊈K。根据已知条件C ⊆B，则如果B ⊆K，那么也有C ⊆K。较早的精确化中建立的事实将会被延续到后面的精确化中。以此类推，我们将得到如图2 的精确化空间：

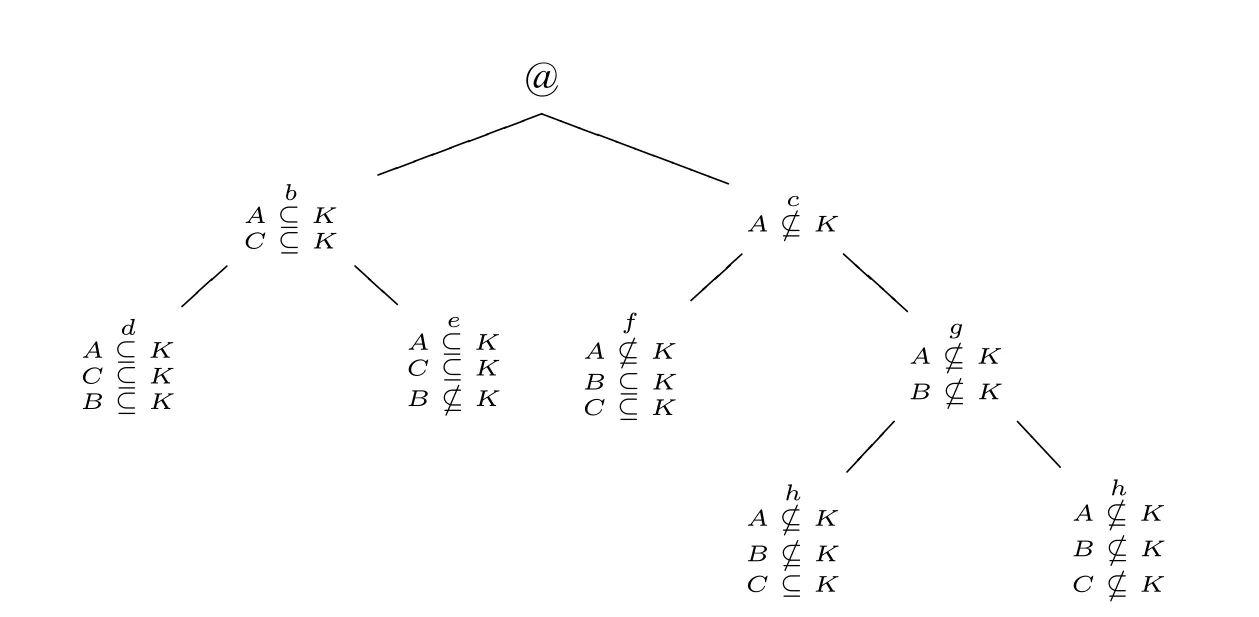
图2

这里只展示了“是否包含于K”这一个事实的精确化，因此可能还有很多精确化仍旧是不完全的（如果一个精确化中还存在语句，该语句且该语句的否定在这个精确化中都不真，则该精确化是不完全的，反之，该精确化是完全的）。范启德认为，任意系列的精确化都将终结于一个完全的精确化。也就是说不定最终能通过精确化达到完全。

设〈P,⊴〉是一个可精确化空间11范启德在原文中先定义了规范空间（specification space，〈P,⊴〉，⊴为偏序关系）（[5]，第271 页），之后又在规范空间基础上定义了满足下文中所列条件的可精确化空间。本文为了突出重点，直接引入了可精确化空间。,12由于秋叶研（[1]）对范启德理论总结所用的符号相对范启德（[5]）中的更为清晰完整且更符合当下的符号使用惯例，因此，这里的论述并未采用[5]中的原版符号，主要参考了秋叶研（[1]）的总结。下文中模态可精确化的偏序空间需要满足条件的符号表达也是如此。，⊴是一个偏序，“q⊴p”读作“精确化q比精确化p更精确”（如果q⊴p且并非p⊴q，我们就称q是p的真精确化，记为q◁p）。其中精确化p,q可看作某种意义上的可能世界，P是可能世界集，⊴可看作可通达关系（因为满足自反性、传递性但不对称13事实上是反对称关系。，所以可看作模态逻辑S4 的特殊情况）。“p⊩P φ”读作“φ在精确化空间p ∈P中为真”或“φ包含于p ∈P”。

范启德进一步总结了一个可精确化的偏序空间P=〈P,⊴〉需要满足的条件：

(1)p⊩P φ ⇔∀q⊴p，q⊩P φ（稳定性）；

(2) 并非p⊩P φ且p⊩P ¬φ（无矛盾性）；

(3)∃q⊴p(q⊩P φ或者q⊩P ¬φ)（可完备化规则）；

(4)p⊩P ¬φ ⇔∀q⊴p,q⊮P φ（否定规则）；

(5)p⊩P φ ∧ψ ⇔p⊩P φ且p⊩P ψ（合取规则）；

(6)p⊩P φ ∨ψ ⇔∀q⊴p,∃r⊴q(r⊩P φ或者r⊩P ψ)（析取规则）；14析取规则在[5])没有直接写出，是秋叶研（[1]）根据文中的内容整理出来的。

(7) 对于每一个完全的p，p⊩P φ ⇔在经典意义上，φ在p中成立（保真性）。根据以上7 个条件，还可推出：

(8) 对任何精确化p和q，如果q⋬p，则存在某个r⊴q使得r与p是不相容的（即，没有s，使得s⊴p且s⊴r）；等价于，∀p∀q(如果∀r⊴q∃s⊴r.s⊴p则q⊴p)（可分离性）。15推论(8)由秋叶研（[1]）根据前七条推出。

直观上，(1)是说一旦一个句子包含于一个精确化空间中，那么它将在这一精确化空间的进一步精确化中一直存在；(2)是说一个句子和它的否定不能同时包含于一个精确化空间之内；(3)是说任何一个句子或它的否定都最终会包含于某个精确化空间之中；(4)是说一个句子不包含于某个精确化空间的任何进一步的精确化之中，当且仅当，该精确化中包含了该句子的否定；(5)是说一个精确化中包含一个合取句，当且仅当，该精确化中包含组成合取句的两个合取支命题；(6)是说一个精确化中包含一个析取式，当且仅当，不管这一个精确化是如何被进一步精确化的，至少有一个析取支会包含于某一更进一步的精确化之中；(7)表明一个完全精确化空间中的真是经典真；(8)是说对任何精确化，如果q不是p的精确化，则存在某一q的精确化r，r与p不相容（即不存在同时是p和r的精确化的s）。

3 基于可精确化结构的超赋值语义

范启德本人基于自己给出的可精确化结构，构建了符合以上条件的超赋值（Supervaluation）语义。在超赋值语义下，一个含糊句为真当且仅当其在所有可达且完全的精确化下都真。换个说法，一个含糊句为真就是在所有使其完全精确的方式下都真。根据可精确化空间需满足的条件(1)，@⊩P ψ即每一个精确化p，p⊩P ψ。因此，在一个可精确化空间下，一个含糊句ψ为真，可记为@ ⊩P ψ。类似的还可以定义含糊句的假。需要注意，在这一语义下，现实世界中本来确定为真、为假的句子，仍旧保持原来的真、假，对于存在边界例子的含糊句，其真、假判断才真正用到可精确化结构。事实上，对于在不同精确化下有真也有假的语句，其解释仍为不定。但在这个语义定义下，

一个语句ψ是有效的，当且仅当对任意的可精确化空间都有ψ为真，即：

⊨ψ当且仅当对任意可精确化的空间〈P,⊴〉，都有@⊩P ψ。“⊨”在这里表示有效。

超赋值语义下的语义后承定义可以整理为：

Γ ⊨ψ当且仅当对任意可精确化的空间〈P,⊴〉，如果对任意的φ ∈Γ，有@⊩P φ（对于每一个精确化p，p⊩P φ），那么@⊩P ψ（即对于每一个精确化q，q⊩P ψ）。16秋叶研（[1]）讨论了超赋值语义的两种可能的语义后承定义方式：SV G（global super valuation）和SV L(logical super valuation)。范启德本人的超赋值语义应属于SV G 模式，由于SV G 模式和SV L 模式的区分对本文的讨论结果没有影响，这里不进一步展开解释。SV G 模式下的单结论模式语义后承定义为：⊨SV G ψ 当且仅当对任意精确化的空间〈P,⊴〉，都有@ ⊩P ψ（即对于@的每一个精确化p，p ⊩P ψ）；Γ ⊨SV G ψ 当且仅当对任意精确化的空间〈P,⊴〉，如果对任意的φ ∈Γ，有@ ⊩P φ（对于每一个精确化p，p ⊩P φ），那么@ ⊩P ψ（即对于每一个精确化q，q ⊩P ψ）。

对于累积悖论，超赋值理论通过认定第二个前提“如果有n根头发的是秃头，则有n+1 根头发的是秃头”假，以此种方式来消除累积悖论。

超赋值解释有不少优点，其一是保留了重言式。尽管有些简单命题（在现实世界中）是不定的，但经典逻辑的重言式仍能够保持有效性。以排中律为例，对语句小赵是秃头（p），其中小赵是秃头的边界例子，则存在现实世界的精确化a和b，其中a中小赵是秃头为真，b中小赵是秃头为假，但不管在a中还是b中（其实是在对于秃的任何精确化中），小赵是秃头或者并非小赵是秃头都为真。这一点，前面提到的三值逻辑解释和模糊逻辑解释都无法做到。图示如下：

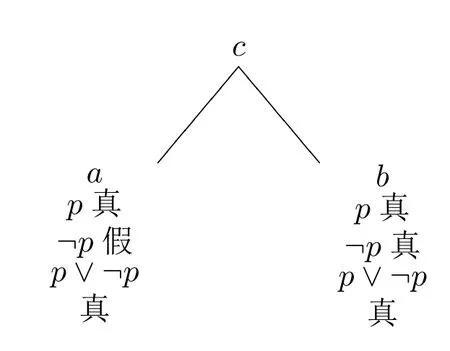
图3

除了重言式，范启德还讨论了半影关系问题。如，设小红是高的边界例子，李琳也是高的边界例子，但李琳比小红高2 厘米，则小红高且李琳不高直观上应为假。但在三值逻辑的解释下，由于小红高和李琳不高的取值都为处于真假之间的不定值I，这一合取式的取值也为I，但在超赋值语义解释下，由于无法给出小红高且李琳不高的精确化，这个合取式为假，符合直观。此外，对于多维含糊的问题，以聪明的为例，可以有记忆力好，反应敏捷，理解力强，综合分析能力强等多维度的聪明，由于可精确化结构是偏序结构，能够表示出不同维度的聪明之间的不可比较性。

范启德指出17参见[5]第284 页：“Thus the supertruth theory makes a difference to truth,but not to logic”。，他的真定义与经典逻辑不同，但逻辑却是一致的，他认为，他所定义的后承关系与经典逻辑的后承关系是一致的。可以证明，在结论是单个公式时，超赋值语义后承与经典逻辑的语义后承是等价的。18需要注意，当给出结论是一个公式集形式的后承定义时，范启德的语义后承定义与经典逻辑中相应的定义不再等价，本文第四节还将讨论这一问题。

但与此同时，超赋值语义不再是真值函数。假设p（例如这个液滴是红色的）是不定的，则¬p也是不定的，然而p ∨¬p是真的。而与之相对的，如果有一个不相关的q（例如小红是高个或这个液滴大）是不定的，则p ∨q通常还是不定的。因此，一般而言，析取式的取值并不是析取支的取值的函数。

同样引入不定来刻画含糊性的边界例子，超赋值语义能够比较精细且符合直观的刻画不定和确定的真、假之间的关系，同时在一定程度上保持经典逻辑，可精确化结构的引入在其中起到了重要的作用。

4 基于可精确化结构的布尔多值语义

基于可精确化结构，是否只有超赋值语义一种解释方式？答案是否定的。秋叶研（[1]）就给出了一种基于可精确化结构的布尔多值语义，这种语义能够满足上一节中给出的可精确化结构中的8 个条件，同时还拥有着比超赋值解释更好的语义性质。

在含糊性问题研究领域，布尔多值语义一直被认为与模糊逻辑“一脉相承”，原因大概在于它们都被归属于多值解释，不同之处在于模糊逻辑方法假定在0 到1 之间的线性有序值（或“度”），布尔赋值则在一个多元的完整的布尔代数中给句子赋值。布尔多值语义可以看作模糊逻辑的进阶版，比模糊逻辑的解释有着更强的表达能力和更好的处理能力。

对于任意布尔代数，B=〈D,∩,∪,-,0,1〉=〈D,⊆〉，这里D是B的域；∩、∪、-分别是下确界、上确界、与B相关联的补集；B的底部和顶部的元素分别是0 和1（任意C ∈B，C ∩-C=0，C ∪-C=1）。⊆是决定B的偏序结构（即自反、传递和反对称关系）。对于经典命题逻辑的一般布尔赋值为：

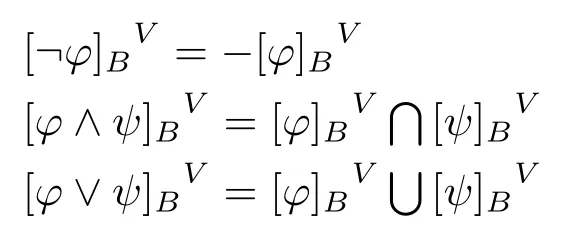
从这个赋值我们可以看出，布尔赋值具有组合性，即一个（复合）公式的取值可以有其组成部分的取值来确定，是真值的函数。同时，对于任意的布尔赋值，有，布尔多值赋值保持了经典逻辑重言式的有效性。

事实上，在D={0,1}时，布尔代数可以退化成经典二值逻辑，但当D中元素数大于2 时，差异就体现出来了。例如，对于D中有6 个元素的布尔代数B6，D={X,-X,U,-U,0,1}，可以构建具有如图4 所示结构的布尔多值赋值。

图4

对于涉及半影关系的例子：设小红是高的边界例子，李琳也是高的边界例子，但李琳比小红高2 厘米，则小红高且李琳不高直观上应为假。在这个布尔多值赋值模型下，设小红高的取值为X，李琳高的取值为U，小红不高的取值为-X，李琳不高的取值为-U，则小红高且李琳不高的取值为X和-U的下确界0（假），与直观相符。

综合以上，布尔多值赋值在保持真值函数的情况下，还能够保持重言式的有效性同时对半影关系免疫。同时，由于布尔多值语义是带有偏序结构的多值赋值语义，也能够避免线序的模糊逻辑在解释多维含糊性时的无奈。

需要注意的是，以上讨论中对布尔赋值的分析是一般性的，这种布尔结构提供了一种赋值框架，具体可以有很多不同的赋值可能。以上分析意味着布尔多值可能可以包容含糊性问题，但布尔多值应用于含糊性问题处理时是否有需要遵循或者可满足的一般化规律？如何更精确的表达出这一点？秋叶研（[1]）中证明了布尔多值处理可以进一步和可精确化结构相融合，或者换个说法，秋叶研给出了基于可精确化结构的一种布尔多值赋值。

要想达成这个目标，核心工作就是要证明一个句子φ在可精确化空间〈P,⊴〉下的赋值等同于P中φ为真的精确化空间所组成的集合，即

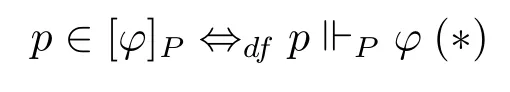
根据布尔赋值的性质，对于否定、合取、析取都是经典的情况，(*) 是直接成立的。但问题在于现在要考虑满足第二节中的条件(1)-(8)的非经典情况，答案是肯定的。秋叶研（[1]）给出了详细的证明，证明的基本思路是，从精确化到布尔赋值的转化中，我们得到[φ]都是正规开集，进而我们可以得到完全布尔代数19正规开集和完全布尔代数的定义详见秋叶研（[1]）。，而在完全布尔代数下p ∈[φ]P ⇔df p⊩P φ(*)成立。

精确化空间到底是如何转化为布尔赋值的？以图5 和图6 的例子展示了从可精确化空间到布尔赋值的转换。

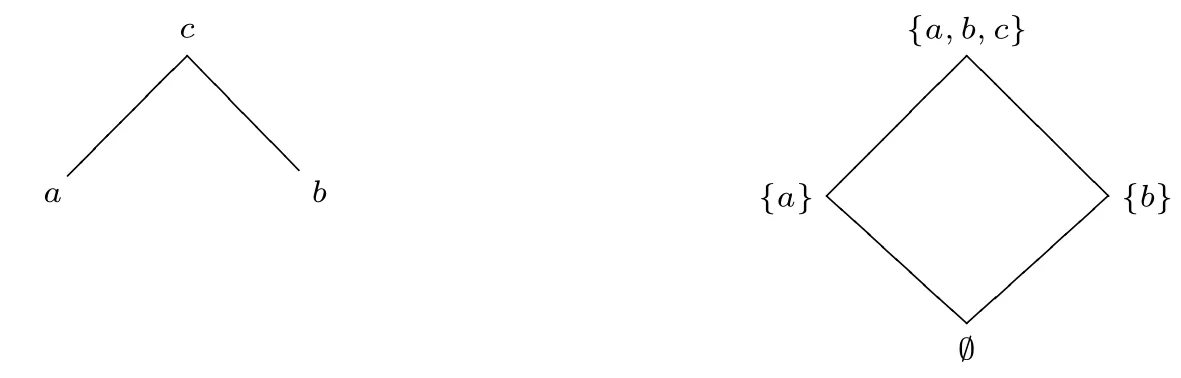
图5

图5 和图6 的左侧图是可精确化空间，右侧图是布尔多值语义的布尔格20格简单来说就是一种可以用代数或关系来表示的数学对象。。在左侧图的可精确化空间下，a,b,c等表示的是精确化（可能世界），而如果x是y的真精确化（x◁y），则精确化x比精确化y的位置要低，在右侧图中，如果x比y的取值更低（x ⊆y且并非y ⊆x），则x处于比y更低的位置。一般而言，一个句子在相对应的精确化空间出现的越晚（越低），其布尔值就越低。如果一个句子在空间中从未出现则取值为0（∅）。

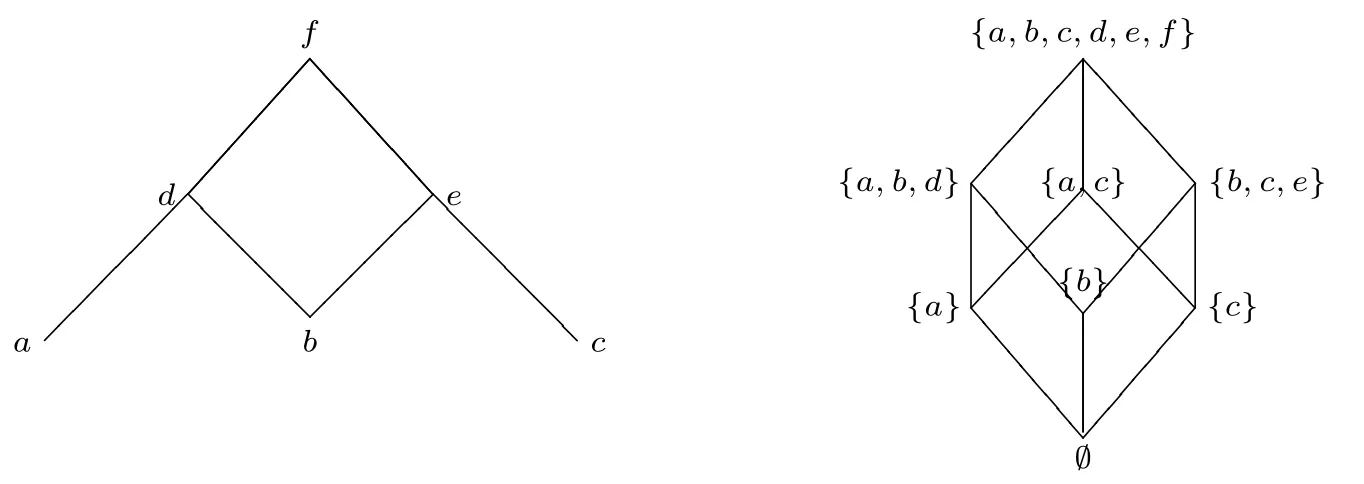
图6

以图5 为例，在左侧图中，对于c中取值为真的公式φ，根据可精确化结构的稳定性（可精确化空间的条件(1)），φ将在c的精确化a,b中继续为真，所以，所有使得φ取值为真的精确化组成的集合即{a,b,c}，与之相对应的就是右侧图中的布尔值{a,b,c}；而左侧图中，假设ψ为c中不定的公式，在c的精确化a中ψ为真，在c的精确化b中ψ为假，则使得ψ取值为真的精确化组成的集合即{a}，与之对应的就是右侧图中的布尔值{a}；{b}的情况与此类似；对于ψ ∧¬ψ，左侧图中没有精确化空间使其为真，也就是使得ψ ∧¬ψ取值为真的精确化集合为∅，与右侧的∅相对应。

以上我们展示了同样基于可精确化结构的布尔多值语义。除了继承超赋值语义的优点，这一布尔多值语义还有一些更好的性质。（一）组合性。首先，在超赋值语义下，联结词不再是关于真值的函数，而布尔多值语义仍旧是真值的函数。超赋值语义并未在真、假、不定之外引入更多的真值，而是通过在真假之间引入可精确化结构来刻画不定逐渐变精确的过程，因此，超赋值语义解释不再是真值函数是个自然而然的结果。而布尔多值语义则直接把可精确化结构投射到赋值上，因此布尔多值语义下，联结词是真值的函数，可以进行真值运算，这也是自然而然的结果。如果联结词是真值的函数，意味着公式的真值获取具有组合性，可以由简单公式的真值，求得复合公式的真值，或者说一个公式的真值可以由它的组成部分的真值所确立，这一点无论从技术处理角度还是转化为计算机应用的角度来讲都是好的性质。（二）后承关系的保持。尽管范启德认为超赋值语义保持了经典后承，但秋叶研分别探究了结论是单个公式的后承定义（Γ ⊨φ），和结论是一个公式集的后承定义（Γ ⊨Δ）两种情况后发现，在Γ ⊨φ模式下，超赋值语义和布尔多值语义都保持了经典后承；但在Γ ⊨Δ 模式下，布尔多值语义定义下的后承仍是经典保持的，但超赋值语义后承不再是经典后承。21SV G 模式下的结论为公式集模式的语义后承定义为：Γ ⊨SV G Δ 当且仅当对任意精确化的空间〈P,⊴〉，如果对任意的φ ∈Γ，有@ ⊩P φ（对于每一个精确化p，p ⊩P φ），那么存在ψ ∈Δ，@ ⊩P ψ（即对于每一个精确化q，q ⊩P ψ）。更多关于是否经典后承的讨论和证明详见秋叶研（[1]）。

综合以上来可以看到，基于可精确化结构的布尔多值语义在保留超赋值语义的优点（具有偏序结构、对半影关系免疫）的同时，还保持了真值函数性，同时在保持经典后承方面进行的更为彻底。

5 对两种基于可精确化结构的语义的一般性评价

尽管布尔多值语义在语义处理的技术层面很“强大”，但不得不说，从直观性角度来看，仍旧是超赋值语义更容易让人理解和接受。我们认为这和人类的认知结构有关，“认知心理学认为，人的思维聚集在所谓的“中型概念”（the middle category concept）周围，所谓中型，主要指心理意义上处在抽象和具体之间的层次”（[14]）。类似的，对于要解释日常现象的理论而言，能够首先被人想到或者被人所广为接受的，大抵是介于抽象与具体之间的“中型层次”的理论。在本文的实例中，超赋值语义某种意义上对应的是中型层次的理论，而基于可精确化结构的布尔多值语义可以看作比中型层次更为抽象的理论。如果接受这样一个理论，就解释含糊性这个具体问题而言，超赋值语义的地位仍旧是不可替代的，没有相对直观和能够让人接受并理解的“中型理论”在先，针对含糊性问题的布尔多值语义恐怕很难被独立给出，或者即使独立给出也很难被广为关注和流传。

从解释含糊性的角度来看。可精确化结构预设了“可精确化”这件事，即，该结构的构建依赖于假设：不定能通过扩充/精确化达到完全22定义上表现为预设了存在完全、可容的规范。，这一假设的合理性是值得商榷的。但不可否认的是，相较于经典三值逻辑和模糊逻辑的处理方式，从不定到真/假的过程添加带偏序的可精确化结构，大大增强了对边界刻画的细致程度。基于可精确化结构，在超赋值解释下，经典重言式（如排中律）得以保持，半影关系可以得到很好的解释，这些都是传统的真值解释无法做到的；然而，在超赋值语义下，真值解释不再是真值函数，尽管在超赋值语义下这算是合理的结果，但从技术角度来看，失去组合性可以算得上一种牺牲。不过，同样基于可精确化结构，秋叶研的布尔多值语义既保持了超赋值语义刻画的优点，又保持了真值函数的组合性，进一步凸显了可精确化结构研究进路作为含糊性解释的优势。

从更一般化的视角来看，秋叶研所证明的结果其实是很顺理成章的。范启德提出的可精确化结构是模态逻辑基底的，对于可精确化空间〈P,⊴〉，在范启德的解释下，P可看作可能世界集，⊴可看作满足自反性、传递性但反对称的可通达关系，所以可看作模态逻辑S4 的特殊情况。而在模态逻辑领域，可能世界的可通达关系本就与布尔代数存在着对应23可参考[3]第5.4 节Duality Theory（第294-303 页）。，因此，基于可精确化结构的这两种含糊性语义其实都属于已有抽象理论在具体问题研究中的应用。不过，这种应用的价值不仅仅在于帮助解决具体问题、解释具体现象，还在于具体应用案例的展示也能够反过来帮助我们反思一般性、理论化的结果之间的关系，乃至这些一般化结果的本质。在含糊性研究领域，超赋值语义一直被当作典型的内涵解释，而布尔多值解释则一直被看作与模糊逻辑的外延解释一脉相承，但基于可精确化结构的布尔多值解释在某种意义上使得“外延解释”与“内涵解释”殊途同归，这不得不让人重新思考“外延语义”与“内涵语义”的关系。接下来我们将重点探讨这一问题。24秋叶研在[1] 的最后一段中也提到布尔语义可能导致内涵和外延的界限变得不清楚：“This seems to blur and call into questions the clear-cut distinction between intension and extension”，但秋叶研没有进一步说明intension 和extension 指什么，也未展开讨论。

6 内涵语义与外延语义之辩

6.1 内涵语义与外延语义的界定

关于内涵语义和外延语义，有不同的观点和界定，本文对内涵语义和外延语义的讨论基于目前较为通行的如下观点：

在命题逻辑层面，外延语义把语句解释为真值；内涵语义把语句解释

为内涵，内涵可以有不同的具体解释，最经典的内涵解释是可能世界到外延（真值）的函数。

在谓词逻辑层面，外延语义把个体词解释为论域中的个体，谓词解释为论域中个体的集合或个体元组的集合；而内涵语义，以基于可能世界语义学的内涵语义为例，个体词被解释为可能世界到个体集合的函数，谓词被解释为可能世界到个体/个体元组的集合的函数。

由于本文给出的含糊性问题解释语义都是命题逻辑层面的，本节中关于内涵语义和外延语义的讨论也只在命题逻辑层面展开，本节以下部分如果没有特殊说明，内涵语义和外延语义均指命题层面的内涵语义和外延语义。具体的，本文选取目前较为主流的内涵解释：内涵是可能世界到外延（真值）的函数。

6.2 内涵语义与外延语义的演进

此种内涵语义与外延语义的界定基于可能世界语义学的兴起。在古典命题逻辑中，一个命题被解释为或真或假的值：一个命题为真就是这个命题与事实情况相符，一个命题为假就是这个命题与事实情况不相符；联结词被解释为真值函项（从真值到真值的函数）。这种解释能够刻画数学推理，但日常语句的一些现象却无法刻画，例如涉及必然、可能的语句：张三必然抽到一等奖和张三可能抽到一等奖这两个语句的真假，无法仅根据张三抽到了一等奖与事实情况是否相符来判断。为了刻画涉及必然、可能的语句，模态逻辑逐渐发展起来，模态逻辑有多种语义，其中影响最大的是可能世界语义。在可能世界语义下，张三必然抽到一等奖在一个可能世界为真当且仅当在这个可能世界所通达的所有可能世界里，张三抽到一等奖，张三可能抽到一等奖在一个可能世界为真当且仅当存在一个这个可能世界所通达的可能世界，在其中张三抽到一等奖。这种解释使一个语句为真的层次扩展了，从只考察当下世界中该语句的真假，变成了一个从可能世界集到真值集的函项。模态逻辑的可能世界语义被看作是典型的内涵语义。

外延语义：语句→真值（真、假）

内涵语义：语句→内涵（可能世界集到外延（真值集）的函数）25这样的处理被刘壮虎称为按“弗雷格路径建立的内涵逻辑”（[11]，第1 页）。

随着时间的演进，可能世界语义学被用到了更广阔的研究领域，除了对可能和必然进行刻画，道义逻辑、认知逻辑、时间逻辑、条件句逻辑、概称句逻辑等领域都可以见到可能世界语义的身影；在含糊性问题研究领域，超赋值语义因为引入了基于可能世界语义的可精确化结构，也被看作是典型的内涵语义解释26参见[5]，第272 页。范启德在文中专门强调了精确化是一个内涵概念：“The account of appropriacy uses the intensional notion of precisification”。，根据本文第二部分的论述，可精确化结构作为一种偏序结构，可以看作是模态逻辑S4-框架的特殊情况。

同样想刻画命题逻辑研究范围之外的语言现象，多值逻辑是另一个进路。1920年，卢卡希维茨试图通过引入真、假之外的第三个值来刻画可能，尽管这一刻画最终没能实现，却导致了多值逻辑的产生。从最初的三值逻辑到在[0,1] 区间的赋值的概率语义，多值逻辑一直没有停下探索的步伐。这一点从含糊性问题的研究中就可以窥见一斑：三值语义和模糊逻辑方向的概率语义都被用来尝试解释含糊性。尤其是概率语义，由于便于计算进而方便转化为计算机应用的特性，在计算机科学相关领域有着不亚于逻辑学领域模态逻辑的影响力，拥有一批拥趸。不过，线序结构的概率语义在解释能力方面有一些局限，在含糊性问题研究领域如此（多维含糊性问题），在概称句研究领域的处理也是如此。科恩（A.Cohen）是概称句研究的概率语义进路的代表人物，在[4]中，他给出了经过反复改良的概称句的概率语义，这种概率语义能够体现概称句具有一定普适性、容忍例外、真值判断以主项和谓项同时作为参数、语境相关性、导致推理非单调等特性，但始终没有办法体现概称句的内涵性，例如，对这台机器榨橙汁这样的概称句，尽管这台榨汁机可能刚出厂还从未榨过橙汁，但我们仍旧认为这两句话为真。但由于这样的语句在现实世界没有实例，在科恩的解释下其概率为0，在这种解释下，概率为0 的句子没有真值，这与人们日常对这类句子的直观并不相符。

以经典三值逻辑、概率赋值为代表的多值语义的本质仍旧是把语句解释为真值，联结词的运算解释为真值函数，区别在于真值集合中的元素由真假二值变成了有穷的多值乃至无穷的多值。由于这一特点，多值语义一直被当作典型的外延语义，是经典二值的外延语义的延展。

外延语义：语句→真值（（真、假），（真、假、不定），…，[0,1]）

内涵语义：语句→内涵（可能世界集到外延（真值集）的函数）

按照上面的演进思路，布尔赋值语义也可以看作一种多值语义，相较线序的概率语义，布尔语义自带偏序结构，可被看作是概率语义的加结构版。

外延语义：语句→真值（（真、假），（真、假、不定），…，[0,1]，带布尔结构的多值）

内涵语义：语句→内涵（可能世界集到外延（真值集）的函数）

6.3 布尔赋值是外延语义还是内涵语义？

然而，秋叶研给出的基于模态可精确化结构的布尔多值语义却让我们反思这一界定下的外延语义和内涵语义的界限。一方面，在含糊性问题研究领域，布尔多值语义作为多值语义一直被看作与模糊逻辑一脉相承。特别的，当D={0,1}时，布尔代数可以退化成经典二值逻辑。另一方面，根据前面的结果，秋叶研给出布尔多值语义可以满足可精确化结构的8 个条件，而由于可精确化结构可看作模态逻辑S4-框架的特殊情况，具有可精确化结构的超赋值语义一直被当作含糊性解释理论中内涵解释的代表。因此，秋叶研的结果提示人们去思考可能世界语义与布尔赋值语义之间的关系。

事实上，在模态逻辑建立之初，就有代数语义学和可能世界语义学两种，甚至代数语义学比可能世界语义学给出的还要早。（[2]）而代数语义学中，如果可及关系满足偏序条件（自反、传递、反对称）就可以用布尔代数来表示。在这个意义上，布尔多值语义到底是属于外延语义还是内涵语义的问题一直存在着，只不过由于含糊性问题研究领域对多值外延进路与模态内涵进路的区分，凸显了这一问题。

那么，布尔多值语义到底是属于外延语义还是内涵语义呢？

外延语义：语句→真值（（真、假），（真、假、不定），…，[0,1]，带布尔结构的多值？）

内涵语义：语句→内涵（可能世界集到外延（真值集）的函数⇔布尔多值语义？）

在模态逻辑领域，布尔赋值与可能世界语义的赋值可以做如下对应：[φ]={w|w⊨φ}27具体而言：[p]= {w|w ⊨p}，[¬φ]= W -[φ]，[φ ∧ψ]=[φ]∩[ψ]，[□φ]= {w ∈W : R(w) ⊆[φ]}，R(w)表示{u ∈W : wRu}。进而可证明，对任意φ，[φ]= {w|w ⊨φ}）。。基于这一结果，我们可以把布尔多值语义转化为这里的内涵语义的形式：给定一个布尔赋值B=〈D,∩,∪,-,0,1,[]〉=〈D,⊆,[]〉，对一个语句φ，其内涵为W →{0,1}的函数，满足：

V(φ,w)=1，如果w ∈[φ]

V(φ,w)=0，如果w/∈[φ]

至此，我们至少可以说，布尔多值语义可以转化为一种内涵语义。

以上对布尔多值语义所作的内涵语义的转化是一般性的，也就是这种转换对布尔多值赋值都是成立的，包括其中的退化情况和特例情况。如，而经典命题逻辑的二值语义是D={0,1}布尔多值语义退化情况；由于线序是一种特殊的偏序（在偏序基础上加上可比较性），所以，概率语义也是布尔多值语义的一种特殊情况。这意味着，经典命题逻辑的二值语义和概率语义这两个典型的外延语义都可以写成内涵语义的形式。

事实上，我们还可以单独给出这些经典外延语义的内涵语义定义。

对于外延语义的“原型”——经典（命题）逻辑的二值语义，其外延集合只有真假两个元素，我们不妨将之记为{0,1}，这个外延集合中的元素也可以表达成内涵的形式28刘壮虎在讨论模态逻辑的邻域语义学时曾提出此转化模式。（[11]）：

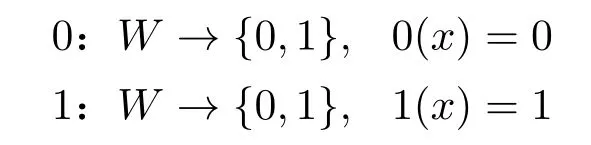
这种表示下，0 作为一个内涵（可能世界集到真值集的函数），将所有的可能世界都映射到外延集合中的元素0 上；1 作为一个内涵，将所有的可能世界都映射到外延集合中的元素1 上。其直观是：一个公式取值为0，即对所有的可能世界，该公式都取值为0；一个公式取值为1，即对所有的可能世界，该公式都取值为1。这意味着，外延可以嵌入中内涵中，因此，在当下的内涵语义界定下，外延语义可以看作一种特殊的内涵语义。这种内涵语义只有两个备选的内涵项。

沿着这一思路，经典三值逻辑和概率语义都可以进行转化。以下只看概率语义的转化29如果依托基于可能世界语义的时态逻辑，具有全序关系的概率语义也可能给出类似布尔多值的内涵语义转化，不过这就是另一项工作了。：

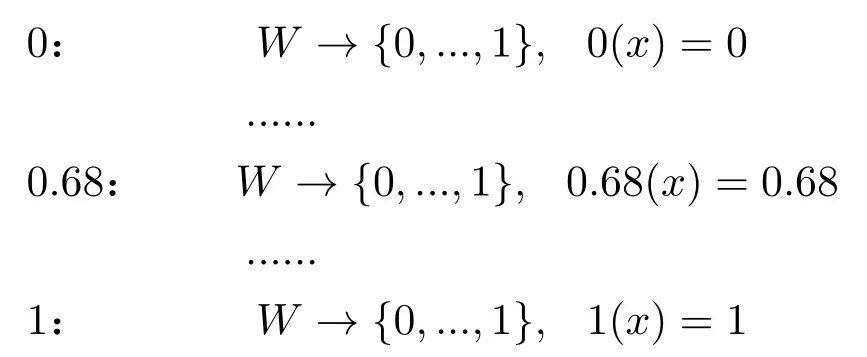
此时，这种内涵语义可以有无穷多个备选内涵，这些备选内涵之间附带着线序关系，即每个内涵之间都可以比较大小。其直观是对每一个语句赋予一个在每一个可能世界都一致的内涵（数字）。

基于以上分析，可以得出结论：这里所定义的外延语义和内涵语义之间是一种包含于关系，外延语义和内涵语义的界定并非一种划分。布尔多值语义作为整体可以转化为内涵语义，经典外延语义如经典二值语义、概率语义也可以看成特殊的内涵语义。

6.4 内涵语义与外延语义的区分究竟是什么？

尽管得出如上结果，但直观上我们仍旧认为外延语义和内涵语义是有区别的。问题在于这种区分的本质是什么？我们该如何表达出这种区分？

在处理自然语言现象和日常推理时，人们发现经典逻辑二值语义是不够用的。例如，在经典逻辑的解释下，由于贾宝玉喜欢的姑娘和美国的女总统在现实中都没有真实存在的对象与之相对应，我们无法区分命题贾宝玉喜欢的姑娘是林黛玉和美国的女总统是林黛玉的真假。但从直观上来看，我们认为贾宝玉喜欢的姑娘是林黛玉为真，美国的女总统是林黛玉为假；再例如，直观上，我们认为命题(1)假若张三身高2.2 米，则张三身高不会超过2.1 米为假，(2)假若张三身高2.2 米，则张三身高会超过1.7 米为真，如果张三的实际身高是1.78 米，则张三身高2.2米为假，如果只使用命题逻辑的二值语义做解释，前件为假的蕴涵式都为真，即(1)、(2)这两句话都为真。研究者们认为，这是由于经典二值逻辑无法体现命题和命题成分30“命题成分”是“原子命题内部成分”的简写，关于命题成分的内涵问题，我们将在第七部分稍微展开讨论。的内涵，因此还需进一步给出能够体现命题和命题成分的内涵的逻辑。

我们知道，经典逻辑建立的初衷是想刻画数学推理的，因此只需使用能够刻画数学推理的研究工具即可，具体体现就是选用适合研究对象的语言和语义。数学语言和数学推理具有精确性和严格边界，经典二值语义这种“理想化”31此处的“理想”与物理领域的“理想气体”、“理想液体”中的理想用法接近。的解释模型能够很好的完成了表达和刻画数学推理的目标。但如果把目光转向不精确的自然语言和具有容错性的日常推理，经典逻辑的工具就不再够用了，需要更丰富的语言和刻画能力更强的语义，于是，就有了关于内涵语义的探索。可能世界语义的引入，最重要是引入了一个带结构的赋值，这使得表达力大大的加强了。另一方面，多值逻辑引入真、假之外的更多的赋值，也是为了增强表达能力。但为什么三值→概率语义被看作是处理外延情况，而布尔多值语义却可以和可能世界语义对应，进而引发外延语义和内涵语义区分的思考呢？

概率语义作为一种特殊的布尔多值语义（满足可比较性的有无穷多个取值的偏序结构），我们看到其与一般布尔多值语义的差别就在于线序结构和偏序结构的差别。数学推理、数学运算都是比较“理想”的线序结构。但是，日常推理则通常是偏序的，有许多不可比较的情况，例如，之前提到的聪明、美等含糊词具有不可比较的多维度，每个人大脑中都可能存在着放在一起会产生矛盾的诸多信念或知识却仍旧运行自如，没有“崩溃”，大抵也是因为偏序（非线序）结构的存在。线序能表达程度上的差异，却无法表达与当下情况并列的其他可能性。偏序的不可比较性在进行计算时是个“麻烦”，但却恰恰是丰富表达的来源，也是表达自然语言和日常推理的恰切手段。

基于以上分析，我们认为，这里所讨论的外延和内涵的区分，或者说我们直观上所理解的日常推理和数学推理的界限，其本质在于是否可以丰富到表达偏序结构，是线序表达32经典逻辑的真假二值也可看作一种线序表达。和偏序表达的区别。因此，随着逻辑语义的理论和应用发展的演进，这一路径下的外延语义和内涵语义的界定应改写为：

外延语义：语句→真值

内涵语义：语句→内涵（内涵解释要可以表达非线序的偏序结构）

“可以表达非线序的偏序结构”的意思是一个语义（类）下存在可以表达非线序的偏序结构的语义解释。

在新的界定下，可能世界语义作为一大类语义的总称，包含了很多不同的框架类型，其中包含了非线序的偏序结构；布尔多值语义同样作为一大类语义的总称，本身就要求具有偏序结构，因此可以表达非线序的偏序结构；因此可能世界语义和布尔多值语义都是内涵语义。经典二值语义和概率语义都是外延语义，同时由于他们都无法表达非线序的偏序结构，它们本身不再是内涵语义，但这些外延语义仍可以作为内涵语义中的外延特例出现，也就是作为一个大类的内涵语义可以包含外延解释特例。另一方面，根据外延语义的界定，布尔多值语义同时也是外延语义。布尔多值语义作为一大类语义的总称，同时符合内涵语义和外延语义的定义。布尔多值语义是解释力非常强大的语义，一方面，它作为代数语义可以解释数学现象；另一方面，由于偏序结构使然，也可以用于日常推理的解释。因此，同时属于两种语义类型，既符合现实也符合直观。

在新的界定下，外延语义和内涵语义之间仍旧不是划分关系，他们之间存在着千丝万缕的联系。但这种界定区分了外延语义和内涵语义，简单来说，不可表达非线序的偏序结构的外延语义可以是某种内涵语义的特殊情况，但它们不再是内涵语义。

7 总结与展望

以上我们从含糊性问题的多值语义和超赋值语义两个进路出发，以布尔多值语义这个连接两种进路的纽带为切入点，详细探讨了命题逻辑层面内涵语义与外延语义的关系。本文指出，基于目前较为通行的内涵语义和外延语义的界定，几种常见的外延语义都可以看作内涵语义的特殊情况，因此外延语义与内涵语义的关系是一种包含于关系，这不符合我们的直观。沿着这一内涵和外延的定义思路，本文通过引入非线序的偏序结构对内涵语义进行了重新界定，在新的界定下，经典二值语义和概率语义作为外延语义是某些内涵语义内部解释下的特殊情况，但外延语义不再作为一种特殊的内涵语义而存在；布尔多值语义作为一个大类，既是外延语义也是内涵语义。

内涵语义与外延语义的区分是逻辑学领域中处在基底的、非常重要的问题，我们应该对什么是内涵语义、什么是外延语义以及它们的区分有更深度的思考。以上我们提供了一种对当下较为流行的内涵语义与外延语义进行修正的方式，是否还有其他的修正方式来界定出这种区分？这是值得更多学者进一步去探索的问题。

基于本文的研究目标，以上的讨论有一些预设和限制条件，例如，对含糊性语义表达能力的评价仅在多值语义和可精确化结构两个进路下已有的研究成果中进行；关于内涵语义和外延语义的讨论基于目前比较常见的一种定义。为了使读者尽可能的看到问题的全貌，以下补充一些预设和限制之外的论题。

7.1 基于可精确化构想的其他语义

基于可精确化构想，除了超赋值语义和布尔多值语义，是否还可能有其他语义？33值得一提的是，同样基于规范空间（〈P,⊴〉，⊴为偏序但不一定满足可精确化的8 个条件）及超赋值语义所定义的真和后承概念，可以给出很多不同的逻辑，如可以给出直觉主义的一个扩充等等。（[5]，第283 页）。但这里探讨的是基于满足8 个条件的可精确化结构是否还有其他的语义，这是两个不同的问题。在模态逻辑领域，除了可能世界语义和代数语义，还有一种更一般化，表达力更强的语义，邻域语义。由此类比过来，基于模态可精确化结构，也很可能可以给出一个邻域语义解释。关于邻域语义，刘壮虎（[10]）通过证明指出：“任何满足组合原则和强的值确定原则的语义学都可以转化成邻域语义学”。34具体可参见[10]，第77 页，其中(1)组合原则：赋值V 由V 在命题变项上的值所确定。这样，所有的赋值都是全体命题变项到值域的映射的扩充。(2)值确定原则(强)：存在R 的子集I(特指集)，使得：一个公式是有效的当且仅当它在任何赋值下的值都在I 中。布尔多值语义满足这一条件，因此，给出基于可精确化构想的邻域语义是可行的。由于邻域语义学也是一种表达力很强的语义，如果给出可精确化构想的邻域语义解释，预期会有更多理论和应用结果的探讨空间。

7.2 含糊性问题的其他解法

以上关于含糊性问题的讨论主要涉及了多值语义进路和模态可精确化进路，而关于含糊性研究还有很多其他的进路，如语用晕理论、情境主义以及容忍度理论等等35关于这几个理论的简介可参见[12]。。特别的，本文所涉及的进路都是命题逻辑层面（把简单命题当作原子）的探讨，通过在赋值过程中添加结构或者更多的真值来表达含糊真与经典真的不同。但由于含糊表达的主体是高、矮、贵、秃头、聪明等语词成分，因此，关于含糊性的另一个自然的研究思路是以这些含糊词以及论域中个体的相似性为主要对象，从简单命题内部的结构入手来探讨含糊性问题的成因。Rooij([7])的容忍度理论和Zhou([9])，周北海（[13]）的含糊类理论都是这一思路下的工作。

7.3 其他路径的内涵语义

刘壮虎把本文中定义的内涵语义和外延语义称为弗雷格路径的内涵语义36原文中用的语汇是“弗雷格路径建立的内涵逻辑”，强调“内涵逻辑”意在与只给出一个语义解释不给出对应的逻辑系统的方式做出区分。本文的讨论重点不在建立某个逻辑（不意味着语义背后没对应着逻辑），而是想讨论不同语义之间的关系，因此替换为外延语义和内涵语义的说法。，他指出：“在这种路径中，无法区分内涵、涵义、命题。如果想区分他们，就要采取另外的途径”。（[11]，第1 页）文献[8]给出了四层语义，通过形式定义区分了内涵、涵义、概念和命题，是“另外的途径”下的一个尝试。当然，这又是另一个宏大的论题了。