关于“现在”算子冗余性的一个注记

孙洋 郭美云

1 引言

指示词（indexical）在人类语言中普遍存在，像“现在”（now），“这里”，“我”等等。上述列举的这类指示词的意义通常依赖于上下文语境，在不同的语境下说出含有这类指示词的句子，往往意味着不同的时间、地点和人。时间指示词（temporal indexical）是一类与时态逻辑关联紧密的指示词，“现在”是最常见的时间指示词之一。

早期的基本时态逻辑只有两个时态算子：过去算子P和将来算子F。尽管如此，基本时态语言却有着极强的表达力，不仅可以做出丰富的时间论述，还可以对时间的结构做出复杂的阐述。随着时态逻辑研究的深入，一些学者开始考虑只包含P，F算子的时态逻辑的表达力是否真的足够。“现在”这一最简单的时态语词，进入到逻辑学家视野之中。

1967 年，坎普（H.Kamp）把他在UCLA（University of California,Los Angeles）研讨班上关于“现在”的逻辑笔记发给了普莱尔（A.Prior），坎普所使用的二维语义方式（two-dimensional approach）对普莱尔带来了很大的启示。普莱尔在[13]中用一维的方式，将坎普的工作整合到了时态逻辑中。他利用混合逻辑，为二维UT演算和包含“现在”算子N的一维时态逻辑建立了桥梁，而且提出了关于“现在”的时态混合逻辑的公理化系统。

坎普在1971 年发表了他关于“现在”的论文（[9]），通过分析“现在”在语言中的作用，提出了二维语义（two-dimensional semantics）解释“现在”算子，同时给出了语境有效的概念。他进而阐述了如何将一般的时态逻辑的公理系统转变为“现在”的时态逻辑公理系统。这篇论文被认为是技术性地研究指示词逻辑（logic of indexical）的起点，他引入的二维语义也被广泛使用于许多领域。

卡普兰（D.Kaplan）将坎普关于“现在”算子的工作进一步提炼并推广到其它指示词，在[10]引入了特征（character）的概念，一个指示词的特征是一个将指示词映射到说话语境的具体事务的函数。例如，人称代词“我”的特征是把“我”投射到给定语境的说话者上。时间指示词，“现在”，“昨天”，“明天”也可以应用“特征”这一概念进行处理。

坎普和卡普兰的工作都是基于一般时态逻辑做的，还可以基于混合逻辑的基础上去做时间指示词的研究。近年来，布莱克本（P.Blackburn）和乔根森（K.Jørgensen）等人在这方面有较多的研究，布莱克本在[3]中指出，用混合逻辑去研究时态指示词更加自然，因为混合逻辑允许提及时刻。布莱克本和乔根森在[4]中对“现在”的混合时态逻辑做了深入研究，采用了由卡普兰推广了的二维语义学和表格系统（Tableau system），证明了逻辑完全性（Logical Completeness）和语境完全性（Contextual Completeness）,进而证明了“昨天”，“今天”，“明天”的混合时态逻辑的完全性。他们还发现时间指示词“现在”在逻辑有效和语境有效之间扮演着某种演绎桥梁（deductive bridge）的作用。而后他们又在[5]中采用了指示时间语义（designated time sematics），这一语义更加接近混合逻辑的标准语义，还构造了“现在”的混合时态逻辑公理系统，并且证明了逻辑完全性。在证明语境完全性时，引入了坎普规则：如果⊢@nowφ，那么⊢φ。并规定这个规则只能在证明中使用一次，而且只能是在倒数第二步使用。他们认为这一规则连接了逻辑有效和语境有效。

时间问题是贯穿于哲学史中的一个基本问题，很多哲学理论都依赖于对时间的不同理解或假定，如柏格森和海德格尔等人的哲学。麦克塔加（J.E.McTaggart）将描述时间的概念区分为A-系列：过去、现在和将来；B-系列：在先、在后和同时。A-系列认为时间总是有一个相对于“现在”的位置，是过去，或者是现在，又或者是将来。因此，A-系列是一种动态的、局部的时间观。普莱尔接受了这种动态时间观并且认为变化是与事件紧密联系在一起的。普莱尔正是基于这样的时间观，创立一个用过去、现在和将来等基本时间概念构造一个关于A-理论时间的逻辑系统，即时态逻辑。A-理论时间哲学家们通常认为只有“现在”才是真实的，过去和将来都不是实在的。所以，他们又常被称作“现在主义者”（Presentism）。

时态逻辑的研究，有助于我们厘清时间问题，同时加深我们对时间的理解。从根本上讲，时态逻辑是关于当前（the present）的讨论，它利用时态算子P、F将当前的信息与过去、将来的信息关联起来，而过去（将来）的信息都曾经（未来）是“当前”的信息。“当前”在时态逻辑中扮演着极为重要的角色，而“现在”又与“当前”有着紧密的联系。“现在”的研究，正是对时态逻辑的初始点进行深入的探讨。

“现在”算子的冗余性，是关于“现在”研究的核心问题之一。普莱尔在[12]中认为“现在”算子是冗余的。而后，普莱尔接受了坎普的观点：“现在”算子是一种二维模态算子，许多性质不同于一维算子。坎普在[9]中证明了在时态命题逻辑中，“现在”算子是冗余的，而在时态谓词逻辑中该算子不是冗余的。他在研究“现在”算子的冗余性问题时，通过引入J-tense 的概念，把真值联结词和时态算子作为一种情形进行处理，造成了证明的晦涩。

本文利用伯吉斯（J.Burgess）证明“现在”算子的冗余性的思路，重新对“现在”算子在时态命题逻辑中的冗余性定理进行证明，补充了简化公式存在性这一关键步骤的证明，并利用证明中的处理方式，来分析自然语言中的时态语句。文章结构安排如下：第二节将对含有“现在”时态句子进行分析，从而讨论时态语言的表达力和“现在”算子的冗余性问题；第三节给出含有“现在”算子的时态语言和语义，以及“语境有效”等概念，进而严格证明“现在”算子在时态命题逻辑中是冗余的；第四节介绍“现在”算子的相关工作并进行了总结。

2 包含“现在”时态句子的逻辑分析

在古典命题逻辑中，命题联结词的完备性问题与语言表达力的问题相关，所有真值联结词都可以被具有函数完备性的联结词集所表达出来。在时态逻辑中也有着语言表达力的问题。首先，我们看一下坎普在[9]中给出的两个句子：

1 一个已经出生的小孩，他会统治这个世界。（A child was born that would become ruler of the world.）

2 一个已经出生的小孩，他未来会统治这个世界。（A child was born that will become ruler of the world.）

论域限定在小孩上，Bx表示x出生。Rx表示x统治这个世界，用Pφ表示过去发生过情形φ，Fφ表示将来会发生情形φ。坎普指出，句子1 可以用时态谓词逻辑形式化为：P∃x(Bx ∧FRx)。

当我们试图去对句子2 进行形式化时，我们失败了。因为句子1、2 中“出生在过去”都是针对说话者说话的时刻即“现在”，而两句话的不同之处在于，“他将统治这个世界”所针对的时刻不同：1 表示他在出生之后将会统治这个世界，2表示他将在“现在”之后统治这个世界。正是基于这样的分析，所以有必要在时态语言中引入“现在”算子（N），“N”算子把他统治世界的时间规定到了“现在”之后。使用加入了“N”算子的时态语言（Nφ表示“现在的情形是φ”），坎普把句子2 可以形式化为：P∃x(Bx ∧NFRx)。

有了“现在”算子N之后，时态谓词逻辑语言是否就可以表达日常生活中的关于时间的所有论述？我们看一下范丙申（J.van Benthem）在[1]中给出的两个句子：

3 有一天，所有现在活着的人都将死去。（One day,all persons alive now will be dead.）

首先使用谓词逻辑语言，范丙申将句子3 形式化为：∃t1(Rtt1∧∀x(Axt →Dxt1))，其中t是自由变元，表示当前时刻，Rts表示t早于s，Axt表示在t时刻x是活着的，Dxt表示在t时刻x是死的。在加入了“N”算子的时态谓词语言中，范丙申将上述句子形式化为：F∀x(NAx →Dx)，其中Ax表示x是活着的，Dx表示x是死的，句子3 的时态关系如图1 所示。含“现在”算子的时态语言是可以表达句子3 的含义，这是由于句子3 没有涉及其他更多更复杂的关于时间的语词。而接下的例子较为复杂：

4 有一天，曾经活着的人们会死去。（One day,all persons alive then would be dead.）

范丙申采用谓词逻辑将句子4 形式化为：∃t1(Rt1t ∧∃t2(Rt1t2∧∀x(Axt1→Dxt2))。如果使用带“现在”算子的时态谓词语言，句子4 只能被形式化为：PF∀x(NAx →Dx)，但它表示在过去将来的某一天，现在活着的人都将死去，即：∃t1(Rt1t∧∃t2(Rt1t2∧∀x(Axt →Dxt2))。范丙申指出它与句子4 所要表达的含义不同。

图1:句子3 的时态关系

图2:句子4 的时态关系

在上例中，“N”算子只能将时间拉回到t时刻，而无法表示出t1时刻。弗拉赫（F.Vlach）在[15]中，指出需要引入“那时”算子（E）才能表达这样的自然语言句子。通过引入“E”算子，可以把时间记录在到t1时刻，使得t1时刻表示“现在”时刻，用Eφ表示“那时的情形是φ”。范丙申指出，句子4 可以形式化如下：PEF∀x(NAx →Dx)，句子4 的时态关系如图2 所示。

句子4 说明，语言表达力不足的问题，在时态逻辑语言中是常见的。由以上句子的形式化，我们直观上可以看出“现在”算子在时态谓词逻辑中并不是冗余。坎普也已经从技术上严格证明了“现在”算子在时态谓词逻辑中并不是冗余的。（[9]）但在时态命题逻辑中，“现在”算子的冗余问题就变得不那么不明显。

普莱尔（[13]）曾举例“现在的情形是我正在坐着”（It is now the case that I am sitting down）和“我正在坐着”（I am sitting down），从日常语言的角度看，这两句话表达的是同一个含义，所以认为是同一个命题，即在“现在”时刻，Np ↔p。这种情况下，N算子显然是冗余的。

接下来，我们看一下这个句子，“将来，我此时此刻是坐着的”（It will be the case that I am sitting down now）,“now”指的是说出整句话的时刻，而此时will 不起作用。“now”将“我坐着”这个动作发生的时间限定在了说话者说出这句话的时刻，而不是将来的某个时刻。再看这两个句子，“将来，我会环游世界”（It will be the case that I travel round the world）和“将来，我现在正环游世界”（It will be the case that I travel the world now）。第二个句子有些奇怪，我们在日常生活中不会那样表述。但是显然这两句话表达的含义不同，所以Fp ↔FNp是不成立的。“现在”算子N在F算子的辖域内，这时把Np替换为p，句子含义被改变了。我们通常认为Np ↔p是成立的，但是如果在N算子从其他时态算子X的辖域中，那么XNp ↔Xp通常是不成立的。但坎普指出在命题时态逻辑中，N算子是冗余的。在N算子从其他时态算子X的辖域中时，我们不能简单得直接将N算子去掉，我们要先把N算子从其他时态算子的辖域中提取出来同时不改变句子的意义，这样再把最外层的N算子去掉，才能达到消除“现在”N算子的目标。第二个句子“将来，我会现在就环游世界”，这个句子包含两部分内容，首先断定了将来存在，然后是“我现在正环游世界”，所以我们认为FNp ↔F⊤∧Np是成立，从而可知FNp ↔F⊤∧p成立。因此，从以上分析可以在直观上表明，N算子是冗余的。下面我们从技术上严格证明这一结论，之后我们还会回到这个例子。

3 “现在”算子在时态命题逻辑的冗余问题

首先，我们给出含有“现在”算子的时态命题逻辑语言和语义，以及语境有效等概念。

定义1.“现在”的时态语言Lnt由命题变元集Prop、命题联结词集{⊥,¬,∧}、基本时态算子{G,H}和“现在”算子N构成。该语言的公式归纳定义如下：

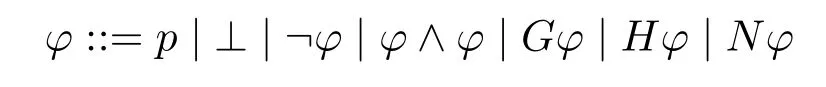
其中p ∈Prop，其他命题联结词采取标准定义。

Gφ表示“将来总是情形φ”，Hφ表示“过去总是情形φ”，Nφ表示“现在是情形φ”。Fφ:=¬G¬φ，Pφ:=¬H¬φ。

定义2.一个时态框架F 是一个二元组(T,R)，其中T是非空集合，R是T上的二元关系。一个“现在”的时态框架是一个二元组(F,n)，其中n ∈T，n表示“现在”的时刻。一个“现在”的时态模型(M,n)是基于时态框架(F,n)的三元组(F,n,V)，V是由命题变元集到T的幂集的赋值函数。

定义3.任给时态模型M 和时刻n,t ∈T，其中,公式φ在模型(M,n)中的t时刻上为真（记为：(M,n),t⊨φ），递归定义如下:

只有当处理形如Nφ的公式时，“现在”时刻n才起作用。

一个公式φ在“现在”的时态框架(F,n)上是语境有效的（记为：(F,n),n|=φ），如果对所有基于(F,n) 的模型(M,n)，(M,n),n |=φ。一个公式是语境有效的，如果它对所有“现在”的框架都是语境有效的。（[9]）一个公式φ在框架F 上是逻辑有效的（记为：F|=φ），如果任给n,t ∈T，任意基于(F,n)的模型，(M,n),t|=φ。一个公式φ是逻辑有效的（记为：⊨φ），如果它在任意框架都是逻辑有效的。“语境有效”的概念实际上就是一般模态逻辑中的“点框架有效”的概念（即一个模态公式χ在一个模态框架H 的一个可能世界w上是有效的，如果对任意基于H 的模态模型N，χ在N 中的w上为真。（[2]）

一个公式是逻辑有效的，那么它也是语境有效的。反之，则不成立。例如，公式p ↔Np是语境有效的，但不是逻辑有效的。由此可知，在逻辑有效的意义上，现在算子N不是冗余的。现在算子N和“现在”时刻n密切相关，所以才定义出了语境有效的概念，语境有效只关注于公式在“现在”时刻的有效性。在语境有效的意义上，“现在”算子的冗余性可以得到更好的讨论。

以下命题在冗余性的证明过程中会使用到。

命题1.(1)φ ↔Nφ是语境有效的。

(2)N¬φ ↔¬Nφ是逻辑有效的。

接下来我们按照伯吉斯的思路进行N算子冗余性的证明，给定含有N算子的公式φ，首先找到一个所有N算子不在其他时态算子辖域内的并且与φ语境等价的公式φR，然后再将所有的N算子去掉得到公式(φR)-，(φR)-与φ语境等价且不含有N算子。由于最后一步去掉N算子，用到了φ ↔Nφ是语境有效的，所以N算子在语境有效的意义下是冗余的。

冗余问题的关键在于处理公式中的N算子出现在G,H算子的辖域中的情况。一旦公式中N算子没有出现在G,H算子的辖域中，我们就可以利用“Nφ ↔φ是语境有效的”（即：将当前时刻点作为“现在”时刻点），从而将N算子去掉。下面我们介绍伯吉斯的简化公式的概念，并且由于在下述证明中使用到了类似古典命题逻辑中的析取范式的处理方式，我们定义该语言的析取范式概念。

定义4.一个公式是简化公式，如果该公式中的N算子不出现在G,H算子的辖域中。如公式:p →NGp，p ∧NG(q →Hp)是简化的，而GNp，G(q →NHp)不是简化的。之后我们使用φR、ψR表示简化公式。

定义5.一个公式是基础公式，如果它是命题变元，或者形如Nχ、Gχ、Hχ，其中χ为任意公式。例如：G(Np →q)，p，NHp都是基础公式。

定义6.一个公式是析取范式φ∨，如果它形如1i ∈n 表示i ∈{0,1,...,n-2,n-1}，∨i∈n j∈mi ψij 即为0≤i≤n-10≤j ≤mi-1 ψij。，每个ψij都是基础公式或者基础公式的否定。一个公式是合取范式φ∧，如果它形如。

析取范式和合取范式的存在定理在之后的证明中会使用到。

定理1.对每一个公式φ，都存在一个析取范式φ∨和合取范式φ∧，使得φ ↔φ∨和φ ↔φ∧是逻辑有效的。

证明.与古典命题逻辑的析取、合取范式存在定理证明类似，详情可参见[8]。

如下定理正是本文要证明的最终结果，即“在语境有效的意义上，现在算子N在命题时态逻辑中是冗余的”。

定理2.对任意公式φ，存在一个不含N算子的公式ψ使得φ ↔ψ是语境有效的。

为了证明N算子的冗余性定理2，我们需要分别证明引理2 和3。处理引理2的归纳步骤中G、H前置的情况，我们需要证明如下的引理1。

引理1.如果ξR是简化公式，那么

(1) 存在简化公式φR使得GξR ↔φR是语境有效的；

(2) 存在简化公式ψR使得HξR ↔ψR是语境有效的。

证明.由于(1)、(2)的证明是类似的，我们这里只证明(1)。由定理1 可知，存在析取范式α，使得|=ξR ↔α。只需证得，存在简化公式φR使得Gα ↔φR是语境有效的。任给框架F 和n ∈T，令(M,n)为任意基于(F,n)的“现在”的时态模型。令α=。因为ξR是简化公式，显然α也是简化公式。

对α的结构分情况讨论：当n=1 时，

· 如果m0=1，则α=β00，即α是一个基础公式或基础公式的否定。

– 当α形如Nχ，

(M,n),n|=GNχ当且仅当 任意s ∈T，如果Rns，那么(M,n),s|=Nχ；

当且仅当 任意s ∈T，并非Rns或者(M,n),n|=Nχ；

当且仅当 任意s ∈T并非Rns，或者(M,n),n|=Nχ；

当且仅当(M,n),n|=G⊥或者(M,n),n|=Nχ；

当且仅当(M,n),n|=G⊥∨Nχ

因为α是简化公式，所以G⊥∨Nχ也是简化公式。

– 当α形如¬Nχ。由于¬Nχ ↔N¬χ是逻辑有效的，处理与上述情形类似。

– 当α是命题变元、或者形如Gχ、Hχ、或者他们的否定时。因为α是简化公式，所以χ中不含N算子。由此可知Gα也是简化公式。

· 如果m0≥2。

如果所有j ∈m0，β0j中均不含有N算子，则Gα就是简化公式。

如果存在β0j中含有N算子，不妨假设只有β00,β01...β0(k-1)中含有N算子，其中k ≤m0。令（注：k=m0时，γ0=⊤），显然α=χ0∧γ0。

(M,n),n|=G(χ0∧γ0)

当且仅当 任意s ∈T，如果Rns，那么(M,n),s|=χ0∧γ0；

当且仅当 任意s ∈T，如果Rns，那么(M,n),s|=χ0并且(M,n),s|=γ0；

当且仅当 任意s ∈T，如果Rns，那么(M,n),s|=χ0，并且，如果Rns，那么(M,n),s|=γ0；

当且仅当 任意s ∈T，如果Rns，那么(M,n),s|=χ0，并且，任意s ∈T如果Rns，那么(M,n),s|=γ0；

当且仅当 (M,n),n|=G⊥∨χ0并且(M,n),n|=Gγ0；

当且仅当 (M,n),n|=(G⊥∨χ0)∧Gγ0。

因为γ0中不含有N算子，所以(G⊥∨χ0)∧Gγ0是简化公式。

（该公式记为:α′′）

因为所有i ∈l,γi和η都不含有N算子，所以α′′是一个简化公式。综上所述，存在简化公式φR，使得Gα ↔φR是语境有效的。

引理2.对于所有公式φ，都存在简化公式φR使得φ ↔φR是语境有效的。

证明.对公式φ的结构进行归纳。

任给框架F 和n ∈T，令(M,n)为任意基于(F,n)的“现在”的时态模型。

·φ是命题变元和⊥时，易得结果；布尔算子的情形，由归纳假设可得。

·φ形如Nψ时，

(M,n),n⊨Nψ当且仅当 (M,n)；

当且仅当 (M,n)（由归纳假设可得）；

当且仅当 (M,n)。

显然ψR是简化公式，所以NψR也是简化公式。

·φ形如Gψ时，

(M,n),n⊨Gψ当且仅当 对任意s ∈T，如果Rns，那么(M,n)；

当且仅当对任意s ∈T，如果Rns，那么(M,n)；

当且仅当(M,n)。

由此可得(F,n)。当ψR中不含N时，GψR是简化公式。但当ψR中含N时，GψR不是简化公式，需要把G辖域内的N提取出来。由引理1 可知，存在简化公式φR使得(F,n)。因此(F,n)

·φ形如Hψ时，与前一条的处理类似。

最后只需证明一个较为简单的引理，就可以完成“现在”算子冗余问题的证明。

引理3.如果一个公式φ是简化公式，那么去掉φ中的所有N算子的新公式φ-满足φ ↔φ-是语境有效的。

证明.对公式φ的结构进行归纳即可证得。

此时，我们可以进行冗余性定理2 的证明。

证明.对任意公式φ，由引理2 可知，存在一个简化公式φR使得φ ↔φR是语境有效的。又由引理3 可知，φR ↔(φR)-是语境有效的。因此，φ ↔(φR)-是语境有效的。

我们再看一下之前的例子“将来，我现在正环游世界”，可被形式化为FNp。由FNp ↔¬G¬Np、GNp ↔(G⊥∨Np)、N¬p ↔¬Np和Np ↔p都是语境有效的，我们可得FNp ↔F⊤∧p是语境有效的，与前文讨论的结果一致。

4 结语

近年来，“现在”算子依然受到学者们的关注。梅耶尔（U.Meyer）在[11]中指出只要使谓词时态逻辑具有足够的量化结构，那么“现在”算子也是冗余的。雅诺维奇（I.Yanovich，[14]）研究了“现在”、“那时”（Then）算子在模态命题逻辑和模态一阶逻辑的模型层次上的表达力，他定义了模态一阶逻辑的互摸拟概念。克雷斯韦尔（M.J.Cresswell，[7]）讨论了谓词区间时态逻辑（Predicate Metric Tense Logic）中含有“现在”语句的形式化问题，以及表达力等问题。

本文主要关注于“现在”算子在时态命题逻辑中的冗余问题，由于坎普原证明的晦涩，本文运用了伯吉斯在[6]中给出的证明思路，重新对“现在”算子在时态命题逻辑中的冗余性定理进行证明。补充了简化公式存在性这一关键步骤的证明，通过将G，H算子辖域内的简化公式转变为析取范式，运用等价公式把N算子从辖域中提取出来。

在坎普之前，对于“现在”的问题就已经有了不少讨论。坎普提出的二维语义使得技术性地对“现在”问题进行研究成为可能，普莱尔和坎普的交流加快了研究的进程。普莱尔对“现在”进行了详尽的分析，随后采用了混合逻辑的途径，在语言中加入表示“现在”时刻的特殊名字n。普莱尔构造了“现在”逻辑的公理系统，用UT演算对这一系统进行了研究。布莱克本沿着普莱尔的路径，构造了新的公理化系统，提出了坎普规则，更合理地捕捉到了语境有效这一概念，进而以此为基础研究“昨天”，“明天”等时间指示词的逻辑。反观坎普，他在基本时态逻辑语言上直接加上“现在”算子N，用二维语义和指示时间语义研究“现在”的相关问题。坎普证明了“现在”算子的冗余问题的结论，他给出了如何从不含“现在”算子的时态逻辑公理系统得到含“现在”算子的时态逻辑公理系统，进而研究新公理系统的可靠性、完全性等性质。二维（多维）语义和引入“名字”的方式各有何利弊，加入“现在”算子和混合逻辑方式的实质性区别，以及造成“现在”算子在时态命题逻辑和时态谓词逻辑中的冗余性的不同的根本原因等问题，都有待进一步研究。