半结构化概率论辩

陈琛 董惠敏 廖备水

1 引言

上个世纪90年代以来，随着抽象论辩框架及其语义理论的提出（[6]）,形式化论辩作为一种新的非单调推理形式，成为人工智能和逻辑学领域的一个研究热点（[22]）。经过二十多年的发展，有关抽象论辩的理论与算法研究（如计算复杂性分析、动态性等方面）已较为成熟（[1,14,15]）。然而，这些理论和算法在实际应用中仍存在局限性，其中一个重要原因在于：未对论证的不确定性进行度量，论证要么存在、要么不存在；同时，论证的状态只有“可接受”、“被拒绝”和“未确定”三种，缺少对中间状态的量化表示。然而，在法律推理、医学推理、多主体协商及说服等实际应用场景中，论证是否存在或可接受并不是完全确定的。在形式化论辩理论里，若缺乏对这类不确定性的适当定量研究，则难以精确地建模各种现实应用中的推理。概率作为一种处理不确定性的经典方法，可以对论证的不确定性加以量化（[11]）。例如，在医学推理中，可能性较小的论证在某些场景下却更为可接受。医生可能会在诊断书上先写道“根据症状，病人应该是受凉了”，随后又写道，“但是考虑到季节，也有比较小的可能性，病人是得了流感”。在这里，后一个论点攻击了前一个论点，即便后者的可能性较小。对这一场景的各方论证，需借助概率作精准的量化表达，显式化元层面信息，并在此基础上进行不确定性推理。于是，在一个论辩框架中针对论证和/或攻击关系新增概率指派，这样的框架被称为概率论辩框架。

由于对论证的概率有不同的理解，现有的概率论辩区分两种方法：群组（constellations）方法和认知（epistemic）方法（[7,13]）。其中，群组方法把论证的概率解释为论证存在或出现的可能性，而认知方法把论证的概率解释为主体相信该论证可接受的程度。这两种方法关注不同的应用场景：前者适合建模因知识的不确定性而引起的论证存在的不确定性，而后者适合建模因主体认知的不确定性而造成的论证可接受性的不确定性。本文聚焦于不完全的客观信息不确定性推理问题，而不考虑主体认知的影响，因此仅考虑群组方法。

依据经典的群组方法，给定一个抽象论辩框架，它的每个子框架对应于一个可能世界，每个可能世界实际存在的概率由子框架中全体论证共同存在的概率所决定（[10,13]）。当这个抽象论辩框架含有n个论证时，按照每个论证是否出现的不同组合，可以构造2n个可能的子框架。同时，由于每个论证被假设为一个“确证点”（justifiedpoint，[10]）彼此独立，论证被接受的概率值仅仅由支持它的因素来确定。此时存在两种指派概率的方法。第一种方法直接给每个子框架指派一个概率。这种方法的优点是不必用概率明确表示各个论证之间的依赖性，无需考虑论证之间是否独立等复杂关联。而此方法的缺点是需要给最多2n个子框架指派概率，建模难度大。同时，值得注意的是，当采用这种方法时，论证之间的存在关联信息是隐含的，从而不具备明确表示该信息的手段。另一种方法给各个论证指派概率，并假设论证之间独立存在。于是，各个子框架的概率由各个论证的边缘概率来决定。这种方法可以降低建模难度，但缺点是无法表达论证之间存在关联的情景。由此带来的问题包括（具体分析详见本文第3.3.2节）：

第一，存在某些论证被接受、但其子论证不被接受的可能。特别地，若子论证对整个论辩过程是必要的，那么这种情况更加不允许发生。

第二，子论证间自相矛盾的情况有被接受的可能。换句话说，即便一个论证的子论证相互攻击，这个论证被接受的概率仍会大于0。于是，矛盾或不一致作为可能事件被接受的概率大于0，这种情况一般应被排除。

第三，没有完整地考虑子论证的防御作用。直觉上，若一个论证能够被其子论证所防御，则在任何该论证出现的可能世界中，它都应该被其子论证防御，而不是只在其中一些可能世界下得到防御，在另一些可能世界下未得到防御。

针对上述三个问题，本文在现有抽象概率论辩的基础上引入子论证关系，构建半结构化论辩框架。它可以用来反映论证之间的存在依赖关系：一个论证的出现蕴含着其子论证的出现，一个子论证的不出现蕴含着其超论证的不出现。在此基础上，引入关于论证的概率，建立半结构化概率论辩理论模型，并研究与论证相关的不确定性推理。

本文结构安排如下。第2节在抽象论辩框架基础上引入子论证关系，建立半结构化论辩框架。第3节在半结构化论辩框架的基础上引入概率，研究半结构化论辩框架的基本特性。第4节总结全文，并指出未来工作。

2 半结构化论辩框架

本节引入子论证关系这个核心概念，建立半结构化论辩框架，同时提出良构概念，研究相关性质。

2.1 Dung-论辩框架与子论证关系

Dung-论辩框架（Dung’s Argumentation framework）由Dung于1995年提出（[6]），它针对不一致情境中的推理，以简洁的方式刻画一个逻辑系统中冲突处理的一般机制（[21]）。Dung-论辩框架仅关注论证及其之间的攻击关系，而不对论证的内部结构进行预设。为简单起见，仅考虑关于有穷多个论证的论辩框架。

定义1(Dung-论辩框架).一个Dung-论辩框架F是一个二元组(A,att)，其中A是一个非空且有穷的论证集，att⊆A×A是在A上的二元关系。

在Dung-论辩框架中，att表示论证之间的攻击关系，而(A,B)∈att表示A攻击B。通过一个论证子集对攻击关系作限制，可得到原框架的一个子框架。给定F=(A,att)，二元组(A′,att′)是它的一个子框架，记作F↓A′，其中A′⊆A且att′=(A′×A′)∩att。为简单起见，用F′⊑F表示F′是F的子框架。给定包含n个论证的Dung-论辩框架，它的每个论证在子框架内有出现和不出现这两种情况，所以它的子框架的数量为2n个。

直接子论证和子论证是论辩理论研究中的常见要素（[4]），可以看作是一种论证之间的支持关系或依存关系。在已有的工作中，Martínez对子论证这一概念做了总体分析（[18]），而Cohen使用子论证和直接子论证来表达论证之间的支持关系（[5]）。从结构化论辩的角度上看，论证A是论证B的直接子论证，就是说A是B的前提。于是，直接子论证关系通常是反自反、反对称、反传递的。从论证出现的概率值来看，一个论证直接支持另一个论证，可以看作是前者存在的概率值影响后者存在的概率值。因而直接子论证关系刻画的是一种论证之间的概率不独立性（[9,19]）。这种概率不独立性是经典的，可用条件概率来表示（[9]）。

定义2(直接子论证关系与子论证关系).给定抽象论证集合A，直接子论证关系subd⊆A×A是一个在A上的反自反、反对称、反传递关系。基于subd的子论证关系sub递归定义如下：

·对于所有A∈A有(A,A)∈sub；

·若(A,B)∈subd则(A,B)∈sub；

·若(A,B)∈sub且(B,C)∈subd则(A,C)∈sub。

当(A,B)∈subd时，A称为B的直接子论证，B称为A的直接超论证。subd(A)可用来表示{B|(B,A)∈subd}，sub(A)表示{B|(B,A)∈sub}。当(A,B)∈sub时，A称为B的子论证，B称为A的超论证。

引理1.给定Dung-论辩框架F=(A,att)和在A上的直接子论证关系subd，存在基于subd的子论证关系sub，使得subd(A)⊆sub(A)。

由子论证关系的定义可直接证明上述引理。

2.2 半结构化论辩框架及其良构性

通过在Dung-论辩框架上添加直接子论证关系，可得到如下半结构化论辩框架的定义。

定义3(半结构化论辩框架).一个半结构化论辩框架Fs是一个三元组(A,att,subd)，其中(A,att)是Dung-论辩框架，而subd⊆A×A是在A上的直接子论证关系。

在做进一步讨论前，需要澄清使用子论证关系表示依赖性的一个基本关系或基本假设：每个论证的直接子论证集是表示依赖性的极小集。换而言之，对于论证A，不存在比直接子论证集subd(A)严格更小的论证集B使得A的出现也依赖于某个B∈B的出现。在直观上，这表明了论证的每个子论证都是必不可少的。这样的假设在一些论辩理论中也很常见。例如，基于可废止逻辑编程的结构化论辩理论（[8]）也要求论证前提集——即此处的子论证集——满足极小性。

此外，需要在子论证关系与攻击关系之间加以限制。首先，避免环状子论证关系的存在。其次，考虑直接子论证关系对攻击关系的影响：攻击论证的直接子论证，则会攻击该论证本身（[3,18]）。这两点限制构成了良构的概念。

定义4(良构).给定Fs=(A,att,subd)和在A上的直接子论证关系subd，Fs对于subd是良构的（well-formed），当且仅当subd是：

1.非循环的（acyclic）：若A1subdA2subd···subdAn，则A1/=An（n≥2）；

2.封闭的：若(A,B)∈att且B∈subd(C)，则(A,C)∈att。良构要求直接子论证关系是非循环的，因此可以将论证作为节点，以直接子论证关系为有向边，构建有向无环图。良构的论辩框架要求在直接子论证关系上对攻击关系封闭：如果直接子论证被攻击，那么它的超论证都受到该攻击者的攻击。若论证攻击自身的直接子论证，则论证会自我攻击。下文的定理8将会讨论，在良构的限制下为什么子论证互相攻击的论证没有被接受的可能。

定理1.给定良构的半结构化论辩框架Fs=(A,att,subd)，那么Fs的子框架F′=(A′,att′)对于subd也是良构的，即：subd依然是非循环的，并且若(A,B)∈att′、B∈subd(C)和C∈A′则(A,C)∈att′。

证明.首先，在Fs中，subd是非循环的，所以subd在子框架F′中依然是非循环的。其次，假设存在(A,B)∈att′，B∈subd(C)，C∈A′且(A,C)/∈att′，那么(A,B)∈att。根框架Fs对于subd是良构的，有(A,C)∈att。由于A,C∈A′，于是(A,C)∈att′。从而subd在子框架中也满足对攻击关系的封闭性。因此F′=(A′,att′)对于subd也是良构的。

例1.根据国家卫生健康委3月发布的《新型冠状病毒肺炎诊疗方案（试行第七版）》，新型冠状病毒肺炎患者的出院标准包括呼吸道症状明显好转、连续两次痰、鼻咽拭子等呼吸道标本核酸检测阴性（采样时间至少间隔24小时）等。与此相关的几个论证如图1所示。

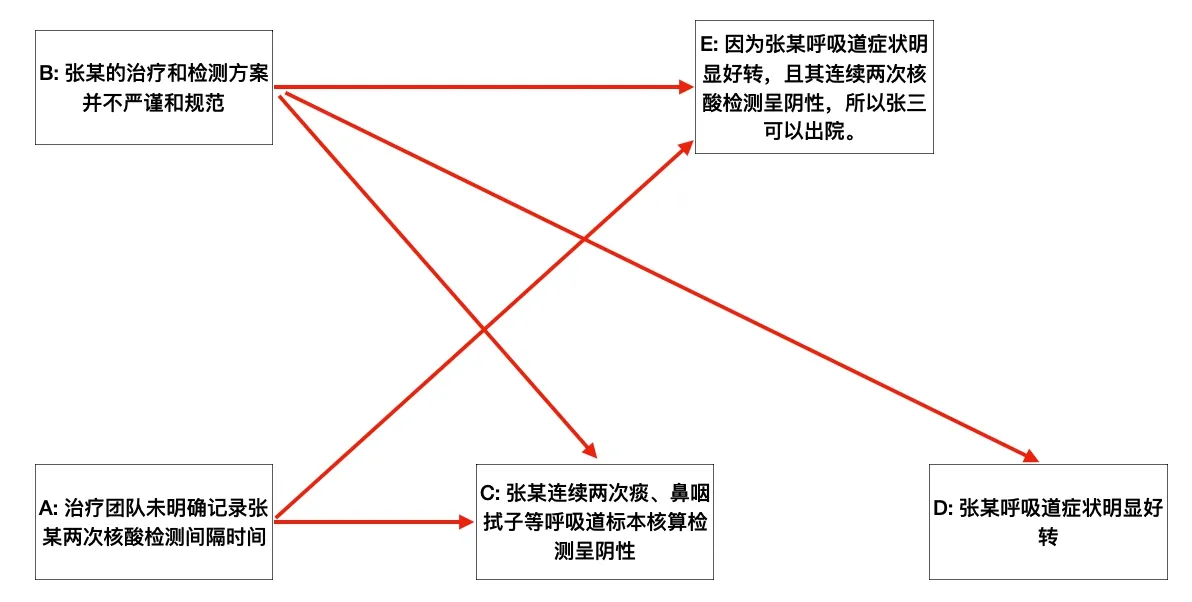
图1:一个关于是否可以出院的论辩场景

用半结构化论辩框架Fs=(A,att,subd)表示该场景，其中：

·A={A,B,C,D,E}；

·att={(A,E),(A,C),(B,C),(B,D),(B,E)}；

·subd={(A,B),(C,E),(D,E)}。如图2所示，这个半结构化论辩框架Fs是一个包含两种有向边的有向图：用实线箭头表示攻击关系，用虚线箭头表示直接子论证关系。这个半结构化论辩框架Fs是良构的。

就框架结构而言，如果在其基础上增加一个直接子论证关系(E,D)或减去攻击关系(A,E)，得到的框架都不是良构的。前者让subd形成了循环D-E-D；而后者让直接子论证关系不再是封闭的，即A攻击E的直接子论证C、却没有攻击E。

接下来，引入子论证深度这个概念，研究一些关于良构的性质。

定义5(子论证深度).子论证B∈sub(A)的深度dgA(B)∈N递归定义如下：任给B∈sub(A)，

1.dgA(B)=0，其中B=A；

2.dgA(B)=min({dgD(B)|D∈subd(A)且B∈sub(D)})+1，其中B/=A。

论证A的子论证深度dgA可定义为max({dgA(B)|B∈sub(A)})。

在图3中，有dgB(A)=1。此外，由于dgC(B)=1，从而dgC(A)=2。当一个论辩框架中的论证个数为无穷时，有可能出现dgA为无穷的情况。例如，如果一个论辩框架的直接子论证关系是循环的，那么dgA是无穷的。

引理2(子论证关系的封闭性).给定半结构化论辩框架Fs=(A,att,subd)，它的子论证关系是封闭的（同定义4），当且仅当：对于所有论证A,B,C∈A，若论证A攻击论证B，且论证B是论证C的子论证，则论证A攻击论证C。

证明.假设Fs=(A,att,subd)上的subd是封闭的。给出(A,B)∈att且B∈sub(C)。我们要证明(A,C)∈att。施归纳于子论证B∈sub(C)的深度dgC(B)=n。

1.当dgC(B)=0时，B=C。因为(A,B)∈att，所以(A,C)∈att。

2.当dgC(B)=n+1时，存在D∈subd(C)使得B∈sub(D)且dgD(B)=n。根据归纳假设和(A,B)∈att，有(A,D)∈att。又因为D∈subd(C)，根据直接子论证关系的封闭性（定义4.2），有(A,C)∈att。

由此可得，若(A,B)∈att且B∈sub(C)，则(A,C)∈att。引理2说明良构的半结构化概率论辩框架的子论证关系也是良构的。

直接子论证关系的封闭性促使某些论证集是选择完全的。具体来说，一个论证集是选择完全的，是指它所有满足攻击封闭性的子论证都在该集合中。满足该特性可避免去接受一个论证而不去接受子论证的情况（[3,19]）。下面的定义参自Riveret等人的工作（[19]）。

定义6(直接子论证完全与子论证完全).一个论证集合E⊆A是直接子论证完全的，当且仅当对于所有A∈E，都有subd(A)⊆E。一个论证集合E⊆A是子论证完全的，当且仅当对于所有A∈E，都有sub(A)⊆E。

例2.继例1，在Fs中，论证集{A,B}是直接子论证完全的，而论证集{C,E}不是直接子论证完全的。因为后者没有把E的直接子论证D也选取进去。值得注意的是，根据子论证完全性，当子论证因其超论证被包括在论证集中时，这个论证也必须被包括在该论证集中。如图3所示，论证A、B、C之间存在着直接子论证关系(A,B),(B,C)∈subd。当这个框架是直接子论证完全时，若C被一个子论证完全的论证集合E包含，则其直接子论证B和子论证A也必然被E包含。当子论证关系具有链状结构时，直接子论证完全的论证集也必然会包含链上的所有元素。

图3:直接子论证与子论证

定理2.论证集合E⊆A是子论证完全的，当且仅当E是直接子论证完全的。

证明.（从左到右）由于E是子论证完全的，对于所有A∈E，都有sub(A)⊆E。又因为有引理1，可知subd(A)⊆sub(A)。从而subd(A)⊆E。所以E是直接子论证完全的。

（从右到左）假定E是直接子论证完全的。对于D∈A，施归纳于B∈sub(D)的子论证深度dgD(B)=n，证明命题(@)：若dgD(B)=n且D∈E，则B∈E。

1.当dgD(B)=0时，B=D，此时可得B=D∈E。

2.当dgD(B)=n+1时，存在C∈subd(D)使得B∈sub(C)且dgC(B)=n。

由于C∈subd(D)、D∈E且E为直接子论证完全，有C∈E。根据归纳假设，由dgC(B)=n且C∈E，有B∈E。

由此证明命题(@)成立。所以，对任意A∈E，有sub(A)⊆E。

受前述的“子论证集极小表示依赖性”的影响，在半结构化论辩框架中，如果接受一个论证，就必须接受该论证的子论证。本文采用基于标记的语义（[12,19,20]）去表示论证的可接受性（[2,6]）。这种方法给每个论证指派一个特定的标签：给定一个半结构化论辩框架Fs=(A,att,subd)，Fs的标记L:A→{in,out,undec}是一个从论证集到标签集的全函数。用in(L)表示{A∈A|L(A)=in}，而out(L)和undec(L)与此相仿。直观上，被标记为in的论证是明确可接受的，被标记为out的论证是明确被拒绝的，而被标记为undec的论证其接受状态是未确定的。在半结构化论辩框架下，首先考虑三种基本的标记：无冲突（conflict-free）标记、可相容（admissible）标记、完全（complete）标记（[2]）。对于标记L，若不存在A,B∈in(L)使得(A,B)∈att，则称L是无冲突标记。一个无冲突标记L是可相容标记，当且仅当：对于所有论证A∈A，

1.若L(A)=out，则：存在B∈A使得L(B)=in且(B,A)∈att；

2.若L(A)=in，则：对所有B∈A，若(B,A)∈att则L(B)=out。一个可相容标记L是完全标记，当且仅当：若L(A)=undec，则，

1.不存在B∈A使得(B,A)∈att且L(B)=in；

2.存在B′∈A使得(B′,A)∈att且L(B′)/out。

完全标记与子论证完全之间有着以下关联。

定理3.L为一个良构半结构化论辩框架的完全标记，则in(L)是子论证完全的。

证明.令Fs=(A,att,subd)是一个良构半结构化论辩框架，L是Fs的一个完全标记。要证明in(L)是子论证完全的，即：任给A∈in(L)，有sub(A)⊆in(L)。对任意B∈sub(A)，要证明L(B)=in。假设L(B)/in，那么存在两种情况：

1.若L(B)=out，则根据L是一个可相容标记，存在C∈A使得L(C)=in且(C,B)∈att。根据引理2，可得(C,A)∈att。又因为前面的证明，已知A∈in(L)且C∈in(L)，这与L是无冲突标记相矛盾。

2.若L(B)=undec，根据L是完全标记，则存在D∈A使得(D,B)∈att且L(D)。再次根据引理2，可得(D,A)∈att。由于A∈in(L)且L是可

相容标记，于是L(D)=out。于是得到了矛盾。

综上所述，L(B)=in。因此，良构的半结构化论辩框架的完全标记L的in(L)是子论证完全的。

基于完全标记，我们可以考察其他类型的论证可接受性与子论证完全之间的联系。基（grounded）标记、优先（preferred）标记和稳定（stable）标记是基于完全标记定义的。对于一个完全标记L:A→{in,out,undec}：

·L是基标记当且仅当in(L)是极小的（在集合的包含关系上）；

·L是优先标记当且仅当in(L)是极大的（在集合的包含关系上）1令⊆为集合2X上的包含关系。Y ∈2X是2X上的极大元，当且仅当¬∃Z∈2X.Y⊂Z。类似地，Y∈2X是2X上的极小元，当且仅当¬∃Z∈2X.Z⊂Y。；

·L是稳定标记当且仅当undec(L)=Ø。

给定一个半结构化论辩框架Fs=(A,att,subd)，用Lσ表示一个σ语义下的标记，其中σ∈{co,gr,pr,st}，分别表示完全标记、基标记、优先标记和稳定标记（[20]）。

推论1.令L为一个良构半结构化论辩框架的σ-标记，其中σ∈{gr,pr,st}。那么，in(L)是子论证完全的。

由于任意的基标记、优先标记、稳定标记都是完全标记，它在良构的半结构化论辩框架下的in(L)，根据定理3，也是子论证完全的。

对于正确评价论证的可接受性来说，良构性或攻击封闭性是很重要的前提条件。若一个半结构化论辩框架不是良构的，则其完全标记、基标记、优先标记、稳定标记下的可接受论证集合不一定是子论证完全的。换句话说，存在一些可接受论证的子论证不被接受。

例3.考虑这个非良构的半结构化论辩框架Fs=(A,att,subd)，其中：

·A={A,B,C}；

·att={(A,B),(B,A)}；

·subd={(A,C)}。

考虑Fs的一个标记L：L(A)=L(B)=undec、L(C)=in。L是完全标记，同时它也是基标记。但是，in(L)并不是子论证完全的——因为C的子论证A没有包含在in(L)中。

良构性让我们在判断论证是否可接受时可以完整地把支持某些论证的所有元素、理由都选择出来（如定理3和推论1）。由此可见，良构性对于保证半结构化论辩框架的结构完整性来说，是有意义的。

3 半结构化概率论辩框架

本节开始在半结构化论辩框架的基础上考虑与概率相关的一些概念。关于概率函数、联合概率、条件概率、全概率公式、条件概率独立性等概念，请具体参考Halpern关于不确定性推理的工作（[9]）。概率函数可以对事件的发生与否给出一个数值，描述事件发生的可能性大小。论证或论证集的是否出现作为一个事件，用概率函数来刻画它的可能性大小。为了简便起见，A和均被称为论证A的相关事件，分别表示“论证A出现”和“论证A不出现”。由论证相关事件构成的集合叫做论证相关集。表示论证A出现而论证B不出现的联合概率，p(A|B)表示当论证B出现时论证A出现的概率。其中，事件A1,···,An的联合出现可记作A1...An。此处，表示论证相关事件A和论证相关事件的联合出现。此外，采用概率论中事件间包含关系⊂来表示论证相关事件之间的包含关系，A⊂B表示如果事件A的出现那么事件B也一定出现。

3.1 半结构化概率论辩框架及其协调性

在半结构化论辩框架的基础上引入概率函数，定义半结构化概率论辩框架。

定义7(半结构化概率论辩框架).一个半结构化概率论辩框架Fsp是一个四元组(A,att,subd,p)，其中(A,att,subd)是一个良构半结构化论辩框架，p是一个关于论证事件的概率函数，它给每个论证是否出现赋概率值。

要注意的是，概率值为0的论证是不被允许的，因为它们可以直接被删除。

此处提出两个理性假设，通过经典的概率独立性（[9]），充分必要地刻画子论证关系之间是相互依赖的：一个论证是另一个论证的子论证，当且仅当以后者的直接子论证为条件时，后者与前者之间不是概率独立的。换句话说，超论证的出现可能性受到子论证是否出现的影响。更具体地，第一个假设描述的是每个直接子论证对于该论证来说都不是独立的。于是，每个论证的直接子论证对该超论证的支持都是必不可少的。这个假设与子论证集的极小性紧密相关。2虽然我们没有假设每个论证的直接子论证集在表达依赖性上是极大的，但此处也并不考虑多组直接子论证共同支持一个论证的情况。如果论证A被n组直接子论证支持，那么实际上并不只是存在A这个单独的论证，而是存在着由这n组直接子论证分别支持的n个论证，只是这n个论证在结构化层面有着相同的关于A的结论。而第二个理性假设要求，在给定论证的直接子论证条件下，如果某个论证与前者不是概率独立的，那么该论证是给定论证的直接子论证。3此处并不考虑非独立的论证之间相互攻击时，一方论证会降低另一方论证的出现概率。为了简单起见，本文仅考虑直接子论证与概率独立性之间的关联；在进一步的工作中，将会考虑其他更为复杂的情形，如直接子论证关系、攻击关系、概率赋值之间的相互影响。以上两个理性假设统称为“协调”。

定义8(协调).半结构化概率论辩框架Fsp=(A,att,subd,p)是协调的，当且仅当：

·对任意A∈A和A1...An∈subd(A)，有A⊂A1...An；

·对任意A∈A和B∈A/subd(A)，A和B是概率独立的。

并非所有的半结构化概率论辩框架都是协调的。下面的例子要说明，当给定的半结构化概率论辩框架不满足协调性的第一个条件时，这会与子论证关系的直觉相矛盾。

例4.给出如图4所示的概率论辩框架Fsp，其中它包含A,B,C三个论证，并且p(A)=0.4、p(B)=0.5、p(C)=0.6，同时B和C都是A的直接子论证。由于p(A)=0.4和p(BC)=p(B)×p(C)=0.3，可得出p(A)＞p(BC)。根据概率函数的性质，可知A/⊂BC。由此可见，超论证A的出现不总是依赖于直接子论证B和C的联合出现。换而言之，当A出现时，有可能某个直接子论证不出现。

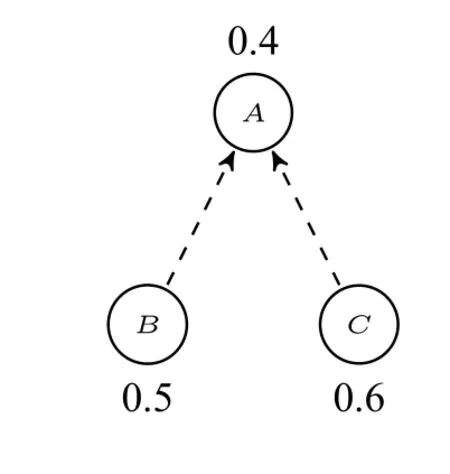
图4:一个不协调的Fsp

进一步地，当一个半结构化论辩框架不满足协调性的第二个条件时，会在子框架概率计算上造成问题。这里使用群组方法计算子框架的概率值。在经典的群组方法（[10]）下，每个子框架被视为一个关于论证是否出现可能世界，在有n个论证的框架中，就有2n个可能世界。子框架概率值等于所有论证相关事件的联合概率。其中，在子框架内的论证是出现的，不在子框架内的论证是不出现的。在已有的群组方法下，可以将所有论证相关事件做简单乘积运算。但是在半结构化概率论辩框架中，计算联合概率需要考虑包含关系，其计算方式如下：给定一个具有论证集合A和概率函数p的半结构化概率论辩框架Fsp和它的一个限制在A′上的子框架F′，那么

其中，Pa(A)={B|B∈subd(A)∩A′}∪是一个以一些论证相关事件为元素的集合。如果不引起歧义，我们也用Pa(A)表示它里面的所有事件的事件积。同时，使用记号来表示论证A不出现在子框架中这一个相关事件。此时，考虑下面一个不协调的半结构化概率论辩框架，将会在子框架的概率计算上得到不合理的结论。

例5.图5给出一个半结构化论辩框架Fsp，一个包含A,B,D,E四个论证的子框架记为F′。经典的概率论辩群组方法假设论证之间是独立的，于是可以通过联合事件的概率乘积来计算F′的出现可能性（[13]），即p(F′)==p(A)×p(B)×p(D)×p(E)×=0.0648，其中表示C不出现在子框架中。但实际上，从直接子论证关系的直观上来讲，A的出现依赖于C的出现：如果C不出现，则A应该不出现。于是，是一个不可能事件，其子框架F′的概率值应该为0。

图5:一个具有字母M形状网络结构的半结构化论辩框架

3.2 论证的可接受程度

一个论证的可接受程度不仅取决于论证出现的概率，而且取决于它出现在哪些子框架中，这是本节的基本假设。前面第2.2节通过基于标记的语义来说明论证在框架中是否被接受，表示论证的可接受性。本节基于子框架的概率值，给出两种关于论证的可能性：论证出现的可能性与论证被接受的可能性。前者指的是论证出现在子框架中的概率；后者又被称为论证可接受程度，指的是在考虑冲突或攻击的情况下，论证有多大概率被接受。后者始终以前者为基础，并受到前者的限制。

首先给出论证出现的可能性的概率计算。

定理4.对于协调半结构概率论辩框架Fsp=(A,att,subd,p)中的任意论证A∈A，

证明.根据子框架的定义，不难看出Fsp的各个不同的子框架F′⊑Fsp之间是互不相容的；同时，每个子框架正好对应于某个论证出现或不出现的组合，因而全体子框架的并等于原框架本身。此时，可使用全概率公式，得到：p(A)=。又因为当A∈A时有p(A|F′)=1，而当A/∈A时有p(A|F′)=0，所以p(A)=。

半结构化概率论辩框架的协调性这个概念可帮助我们更好地分析每个论证被接受的可能性。这种可能性可看作所有的包含这个被标记为in的论证的子框架的概率值之和，反映出单个论证本身的可接受程度。在给定的框架中，通过引入“蕴含”这个概念，说明一个论证是否在一个框架上可接受。将Fσ-蕴含E记为F⊢σE（[10]），当且仅当存在一个在框架F上的σ-标记L使得in(L)=E。若不引起歧义，可简写为F蕴含E。下面介绍如何刻画论证本身的可接受程度，这属于半结构化概率论辩框架的语义部分。

定义9(论证被标为in的概率).令Fsp=(A,att,subd,p)是一个协调的半结构化概率论辩框架，E⊆A为一个论证集合，且σ∈{co,gr,pr,st}。一个论证A∈A被σ-标记标为in的概率，记作p(Aσ)，被定义为，其中Iσ(A)={F′⊑Fsp|F′⊢σE且A∈E}。

例6.用半结构化概率论辩框架的语义对图6中的框架进行计算，得出在基语义下，E论证被gr-标记标为in的概率为0.35。相比之下，如果用群组方法直接进行计算（不考虑子论证关系对概率值的影响），则相应的结果为0.315。

图6:基于子论证关系对Fsp的概率值进行计算

在协调的半结构化概率论辩框架下，一个论证的可接受程度总是小于它自身出现的可能性。

定理5.给出一个协调半结构概率论辩框架Fsp=(A,att,subd,p)，对任意论证A∈A，有p(Aσ)≤p(A)。证明.根据定义9，p(Aσ)=，其中Iσ(A)={F′⊑Fsp|F′⊢σE且A∈E}是所有包含了被一个σ-标记记为in的论证A的子框架。令FA={F′|F′=(A′,att′)⊑Fsp,A∈A′}是所有包含A的子框架。根据这两个集合的构造，一个子框架若存在一个σ-标记将A被标为in，则这个子框架必然包含A，即Iσ(A)⊆FA。因此，。根据定理4，，所以。可见，一个论证的σ-接受度受到相应σ-标记的限制。

以上论述说明了，每个论证的可接受的概率由相应子框架的概率值之和所决定，但必须小于这个论证出现的概率。在直观上，论证出现的概率只要考虑对论证支持的因素，而论证可接受的概率需要进一步地考虑冲突与矛盾。所以，后者相对前者只可能严格更小（当受到攻击时）或者相等（当未受到攻击时），而不会更大。

3.3 协调半结构化概率论辩框架的重要性质

3.3.1 子框架与子论证完全

对于一个子框架而言，只有当它的论证集是子论证完全的时候，这个子框架才完整地考虑了论证之间的依赖关系。这样的子论证完全框架，它们的概率值不为0，因而是我们关注的对象。

定义10(子论证完全框架).对于一个协调的Fsp的子框架F′=(A′,att′)，我们说F′是子论证完全框架，当且仅当：A′是子论证完全的。

给定协调的半结构化概率论辩框架Fsp，其本身一定是子论证完全的，但其子框架可以按照是否是子论证完全框架分为两类。这是因为子框架的论证集是原框架的论证集的子集（见第2.1节）。而根据对子论证完全性的定义（见定义6），子框架的直接子论证关系是根据原框架的直接子论证关系来定义的。因而，可能存在一个在这个论证子集中的元素，它的子论证不一定在这个论证子集中。比如，例6中的子框架({B},Ø)就不是子论证完全的。

与子论证完全框架相比，可以采用框架出现的可能性来划分子框架，其中概率值不为0的子框架是合法，而概率值为0的子框架是非法的。

定义11(合法子框架与非法子框架).对于一个子框架F′，若p(F′)/=0，则是合法子框架，否则是非法子框架。

定理6.若子框架F′不是子论证完全框架，则F′是非法子框架。

证明.令F′=(A′,att′)不是一个子论证完全子框架，则A不是子论证完全的。根据命题2，可得知A不是直接子论证完全的。于是，存在A∈A′，(B,A)∈subd且B/∈A′。因为(B,A)∈subd且框架是协调的（定义8），有A⊂B。再次根据条件概率，可知×p(A)=(1-p(B|A))×p(A)=0×p(A)=0。又因为A在F′中，B不在F′中，由此可得p(F′)=0，即F′是非法子框架。

例7.例5中的M型的协调半结构化概率论辩框架，存在包含A,B,D,E四个论证的子框架F′。这个子框架它不是一个子论证完全框架，同时它的概率值为p(F′)=0，它是非法子框架。

3.3.2 论证可接受程度的三种表现

协调半结构化概率论辩框架所具备的良好性质，可以通过与论证接受程度相关的三个命题来表现。它们与本文的研究动机紧密相关。

首先，在这样的概率论辩框架中，不会出现一个论证被接受但其子论证不被接受的情况。换句话说，如果一个论证集E在原框架中是完全接受的却又存在不被接受的子论证，那么完全接受它的子框架就不会是子论证完全框架。这样一个论证集被接受的可能性为0。一个论证集被接受的可能性可以通过概率来定义，被称为这个论证集的可接受程度。

定义12(论证集被标为in的概率，[10]).令E⊆A为一个论证集，Qσ(E)为σ-蕴含E的子框架集，其中σ∈{co,gr,pr,st}。E被σ-标记标为in的概率p(Eσ)定义为全体的σ-蕴含E的子框架的概率值之和：

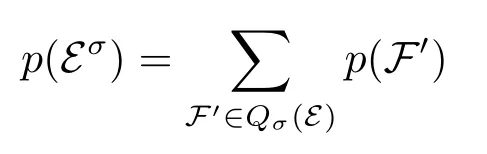
要注意的是，Qσ(E)中的子框架都是将E作为接受集in(Lσ)的子框架。因此，一个论证集E的接受度便由接受它的子框架所决定。

定理7.在协调的Fsp=(A,att,subd,p)中，如果一个论证集E⊆A不是子论证完全的，那么p(Eσ)=0，其中σ∈{co,gr,pr,st}。

证明.令E⊆A且F′∈Qσ(E)。此时F′=(A′,att′)有两种可能性：是子论证完全框架或不是子论证完全框架。

1.假如F′是子论证完全框架，那么A′是子论证完全的。由于F′∈Qσ(E)，令L为F′上的一个完全标记，于是E=in(L)⊆A′。因为E不是子论证完全的，于是∃A∈E且∃B∈sub(A)使得B/∈E。因此有A∈in(L)且B/∈in(L)。由于F是良构的，那么它的所有子框架F′都是良构的。根据定理3，当L为良构的F′上的一个完全标记时，其接受集in(L)=E是子论证完全的。由于A∈in(L)且B∈sub(A)，必定有B∈in(L)。这与B/∈in(L)矛盾。因此，不存在F′∈Qσ(E)使得它是子论证完全框架。

2.当F′不是子论证完全框架时，根据定理6，此时p(F′)=0。综上所述，Qσ(E)的元素均不是子论证完全框架。故p(Eσ)==0。

于是，在协调的半结构化概率论辩框架中，只有子论证完全的论证集合被标为in的概率才能不为0，即它的可接受程度不为0。

例8.如图7，“明天不下雨”的概率为0.5，“明天不下雨，所以明天去爬山。”的概率为0.4。但是在原先的群组方法概率论辩框架中，用B表示“明天不下雨”，用A表示“明天不下雨，所以明天去爬山”。计算出{A}（请注意，这个集合不包括B）被标记为in的概率是0.2，即存在20%的可能性是接受A但是不接受B的。然而，当重新检查例子时便会发现，这很难在不接受“明天不下雨”的情况下去接受“明天不下雨，所以明天去爬山”。而在协调半结构化概率论辩框架中，p({A}σ)=0，其中σ∈{co,gr,pr,st}。这体现出本框架对原先群组方法的修正。

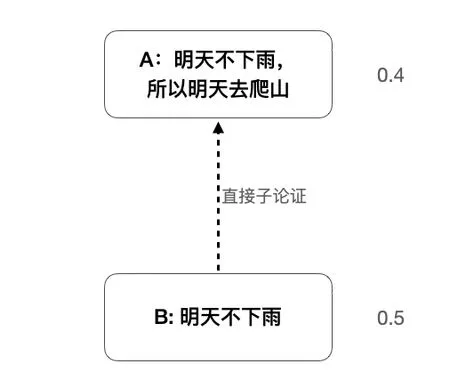
图7:不下雨去爬山

其二，在协调的半结构化概率论辩框架中，当子论证攻击超论证时，这个超论证是不可能被接受的。换句话说，此时该论证被标为in的概率为0。

定理8.对于协调的Fsp=(A,att,subd,p)中的任意论证A∈A，若存在论证B∈sub(A)且(B,A)∈att，则p(Aσ)=0，其中σ∈{co,gr,pr,st}。

证明.令F′∈Iσ(A)={F′⊑Fsp|F′⊢σin(L)且A∈in(L)}。又令B∈sub(A)使得(B,A)∈att。此时F′有两种情况：

1.假如F′=(A′,att′)是子论证完全框架。此时A′是子论证完全的。由于F′∈Iσ(A)，令L为F′上的一个完全标记，根据定理3，此时有in(L)⊆A′是子论证完全的。据此，由于B∈sub(A)，于是有B∈in(L)。同时，由于B∈sub(A)且A∈A′，根据A′是子论证完全的，可知B∈A′。于是(B,A)∈att′。但由于A∈in(L)、(B,A)∈att′且L是一个F′上的可相容标记，可知B∈out(L)。但B不可能同时被一个标记标为in和out。于是，并不存在F′∈Iσ(A)使得它是一个子论证完全框架。因此，Iσ(A)中的元素均不是子论证完全框架。

2.假如F′不是子论证完全框架，根据定理6，此时p(F′)=0。根据上述分析，可知p(Aσ)=

因此，只有不被子论证攻击的论证，才有被接受的可能性。

例9.“自相矛盾”的论辩场景出自于《韩非子·难一》，如图8所示，其中论证的概率值来自知识的不确定性引起的论证的不确定性。如果用Fp对其进行建模，则“因为我的矛是世界上最好的矛，我的盾也是世界上最好的盾，所以我的武器都是世界上最好的。”这个本身包含矛盾的论证最终被接受的概率值为0.036，而不是不为0，因而存在着矛盾被接受的风险。而若是用Fsp对其进行建模，令A表示“因为我的矛是世界上最好的，我的盾也是世界上最好的，所以我的武器都是世界上最好的。”，则p(Aσ)=0，其中σ∈{co,gr,pr,st}。

图8:自相矛盾例子图示，其中文字框表示论证，文字框旁的数字是该论证的概率值，红色实线箭头表示攻击关系，黑色虚线箭头表示直接子论证关系。

第三个研究动机是要去探讨在何时一个论证在完全标记下的可接受程度与其自身出现的可能性相等。

定理9.给定协调的Fsp=(A,att,subd,p)。对任意论证A∈A，若满足：

a1.不存在论证B,C∈sub(A)使得(B,C)∈att；

a2.对所有论证D∈A，若(D,A)∈att，则存在论证K∈sub(A)使得(K,D)∈att。

那么，p(Aco)=p(A)。

证明.根据定义12和定理4，需要证明：对任意子论证完全子框架F′，如果A∈A′，那么存在一个在F′上的完全标记L使得L(A)=in。根据定理8，此时仅需要考虑那些作为子框架完全框架的子框架F′。令F′=(A′,att′)是任意一个包含A作为节点的子框架完全框架，按照如下方式构造一个F′的标记L：

1.若B∈sub(A)，则L(B)=in；

2.若(B,A)∈att′，则L(B)=out；

3.若B/∈sub(A)且(B,A)/∈att′，此时考虑三种情况：

(a)若∃C∈in(L)使得(C,B)∈att′，则令B∈out(L)；

(b)若(C,B)∈att′⇒C∈out(L)，则令B∈in(L)；

(c)若¬∃C∈in(L).(C,B)∈att′且∃C/∈out(L).(C,B)∈att′，则令B∈undec(L)。

可见，(a)、(b)、(c)这三种情况完全覆盖了情况(3)。

首先，L是无冲突标记。否则，存在B,C∈in(L)且(B,C)∈att′。这里有如下两种情况：

·若B,C均由情况(1)产生，此时B,C∈sub(A)。但根据条件(a1)，(B,C)/∈att。根据att′⊆att，于是(B,C)/∈att′。这产生矛盾。

·若C由情况(3b)产生，又因为(B,C)∈att′，所以B∈out(L)。此时与B∈in(L)矛盾。

因此，L是一个F′上的无冲突标记。

接下来证明L是F′的完全标记。对任意论证B∈A′，

·如果L(B)=in，那么：当(C,B)∈att′时，

1.若L(B)=in由情况（2）得出，则B∈sub(A)。因为F是良构的，所以G′也是良构的，根据良构的定义以及(C,B)∈att′，可得(C,A)∈att′，根据情况(2)，则C∈out；

2.若L(B)=in由情况(3b)得出，则C∈out(L)。

·如果L(B)=out，那么：

1.根据情况(2)，有(B,A)∈att′，所以有(B,A)∈att，根据条件a2，存在C∈A使得C∈sub(A)且(C,B)∈att。根据情况(1)，L(C)=in。又因为G′是子论证完全框架，从A∈A′和C∈sub(A)，可得C∈A′。由于B∈A′，于是(C,B)∈att′。所以存在C∈in(L)使得(C,B)∈att′；

2.根据情况(3a)，存在C∈in(L)使得(C,B)∈att′。

·如果L(B)=undec，那么，根据情况(3c)，得到满足可相容标记的条件。

所以，标记L为F′的完全标记，并且它满足要求：A∈in(L)。

据此，在协调的半结构化概率论辩框架中，若一个论证A的子论证间没有攻击，且对于每个攻击A的论证，都存在A的子论证来防御A，那么A在完全外延中的可被接受的概率就是A出现的概率。以上命题完整地表达出子论证对论证的防御作用。

例10.考虑如下图抽象论辩，其中A是B的直接子论证，若用原先的群组方法概率论辩框架，则无法表示出A和B之间的子论证关系，所以在完全语义下，B被完全标记标为in的概率p(Bco)=0.38≤p(B)。而用半结构化概率论辩框架建模，可得p(Bco)=p(B)=0.5。

4 结论

本文工作在于针对经典群组方法（[10,11,13]）中三个方面的性质进行补足和修正：外延的不完全性、接受矛盾的可能性和子论证防御作用的不完整性。通过在原先的群组方法概率论辩框架下加入直接子论证关系，重新定义可靠的半结构化概率论辩框架及其语义，同时研究与相互依赖的论证所紧密关联的性质。要指出的是，在半结构化概率论辩框架中，概率不为0 的论证与它的子论证之间是不可能出现矛盾的，并且这样的超论证能完全得到其子论证的保护。

此处提出的半结构化概率论辩框架，首次系统全面地分析子论证关系对概率赋值、框架结构、概率语义、关于矛盾、防御等概念所产生的作用。与此相比，以往的概率论辩研究并没有考虑子论证关系，而是从其他层面上给出关于论证的概率赋值，比如在结构化层面（[7]），在语言层面（[19]），在抽象论证层面（[10]），在子框架层面（[19]），以及在论辩框架整体层面（[12]），研究其他不确定性推理的相关问题。

在此基础上，可以从以下三个方面做进一步的研究。第一，将半结构化概率论辩框架应用于对不同实际推理场景进行建模，包括法律推理、医学推理、军事推理、日常推理等，同时根据实际需要进行理性假设、调整概率论辩框架。第二，在半结构化概率论辩框架基础上，借鉴群组方法（[17]），分析如何降低概率论辩的计算复杂性、提高效率。第三，将半结构化表示方法推广至包含偏好关系的论辩理论中（[16]）。