基于正则化等效源模型的航空重力梯度测量信息降噪方法

赵德军，孙中苗，赵东明，谢心和

（1.信息工程大学地理空间信息学院，郑州 450001；2.西安测绘总站，西安 710054；3.地理信息工程国家重点实验室，西安 710054；4.西安测绘研究所，西安 710054）

航空重力梯度测量以其快速高效、机动灵活以及超高空间分辨率的优势，在油气勘探、固体矿产勘查、地理信息构图和科学研究中发挥着越来越重要的作用。根据测量重力梯度的分量情况，可以分为以FALCON 为代表的部分张量梯度测量系统和以Air-FTG 为代表的全张量梯度测量系统两类。航空重力梯度测量能获取多个梯度分量，然而在不破坏其内部一致性的情况下处理多分量航空重力梯度数据是一个巨大的挑战。

等效源法利用一系列简单的虚拟地质体代替真实场源进行重磁场建模，通过虚拟地质体的正演对重磁场信息进行重构。等效源法重构重力场的目标是使虚拟场源产生的重力场无限接近真实的位场，其目的是恢复空间场值，而不是对真实场源的准确重建，不考虑地下空间的三维密度反演[1-6]。所以，通过构建合理的、简单的等效场源模型，可以大幅减少计算难度。一般用长方体、圆柱体或球等规则几何体来表示等效源模型，如果规则几何体压缩成没有体积的点，则等效源模型就简化为大地测量领域的点质量模型。

等效源模型可以直接处理原始离散点上的观测数据，能够联合解算不同类型、高度及分辨率的重磁数据，因此被广泛用于重磁位场数据处理。在重磁领域，等效源法被用于位场数据的转换[1]、延拓[4]，以及多源重磁数据的融合[6]等。等效源法非常适合于重力梯度这样的多分量数据处理，因为每个重力梯度分量都是由相同的地质体引起的。利用等效源模型重建重力梯度，能保持多个梯度分量之间固有的内在联系。

但是，求解虚等效源模型所涉及的矩阵求逆常受到观测误差的影响，使数值解算失稳，可能出现病态性问题，因此需运用正则化方法处理其法方程的病态性。Tikhonov 正-则化方法在解决病态方程上得到了广泛的应用，文献[7-9]的讨论均以Tikhonov 正则化为基础。截断奇异值TSVD 方法也是解决病态性问题的一种重要方法[10]。本文将TSVD 和Tikhonov 正则化方法引入等效源模型解算，以抑制设计矩阵的病态性，实现多分量航空重力梯度的降噪，以及不同重力梯度分量之间的转换。

1 等效源原理

1.1 基本理论

矩形棱柱体作为最常用的模型构建单元被广泛应用于重力梯度正演数值模拟之中。在局部直角坐标系——北东下NED，即x轴指向北，y轴指向东，z垂直向下，单个矩形棱柱体场源正演重力梯度张量和重力异常（大地测量邻域称为扰动重力）的无奇点解析公式为[11]：

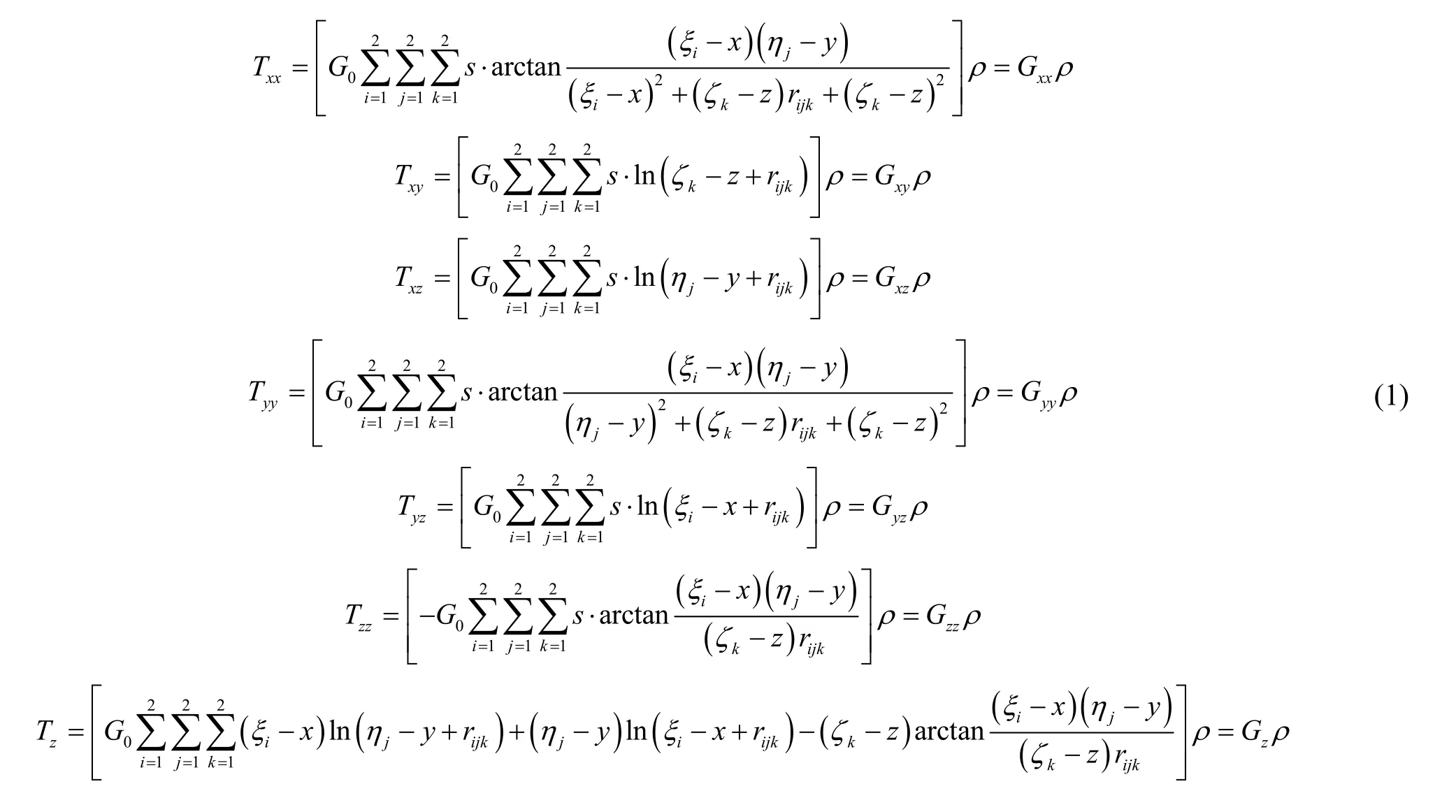
从式(1)可看出，若已知计算点的坐标和长方体的坐标，则正演的重力梯度张量与密度ρ成线性关系：代表式(1)等式右端的线性系数项。假设埋藏的等效源共n个,则第i个观测点的梯度分量为n个等效源的和：

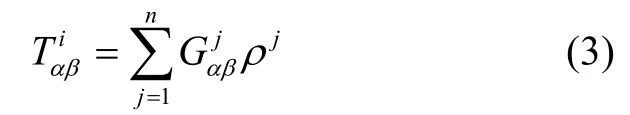
观测到的梯度数据位于三维空间中不规则分布的点上，若有m个观测数据，则有：

将式(4)写成矩阵形式：

式中L为m阶的梯度观测值向量，X为n阶的等效源密度向量，A为联系已知观测值和未知密度的m×n阶系数矩阵。根据最小二乘理论，可在均衡多个重力梯度信息的基础上，得到自洽的密度参数估值：

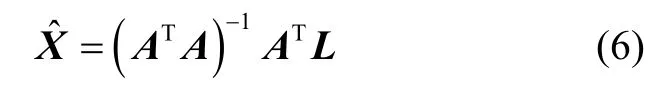
1.2 正则化改造

1.2.1 正则化方法

由于虚拟等效源解算过程可能存在欠适定性，因此若不采用特殊的方法求解，将得不到合理的估值。对观测矩阵A进行奇异值分解，就会发现观测方程病态的根本原因：系数矩阵A的一系列奇异值中存在减趋于零的奇异值，正是由于存在这些特别小的奇异值，导致很小的观测噪声也会引起待估参数较大的偏差[7]。要想获得稳定的等效源解，必须对不适定方程进行正则化改造，以抑制观测误差对待估参数的影响。为了获得稳定的参数估值，需要根据病态观测方程的特点，构建正则化解，常用的正则化方法有截断奇异值TSVD 和Tikhonov 正则化。

截断奇异值TSVD 法，顾名思义，首先将病态观测方程进行奇异值分解，然后通过截掉系数矩阵的小奇异值和对应的特征向量，最后仅利用大的奇异值和对应的特征向量构建参数估值。通过这种抛弃系数矩阵小奇异值的方法，从而避免放大高频观测误差对参数估值的影响。

对系数矩阵A作奇异值分解[10]：

式中，U是A的左奇异向量矩阵，为m×n的正交矩阵；V是A的右奇异向量矩阵，为n×n的正交矩阵；Λ是n×n的对角矩阵，其对角线上的元素为A的递减的奇异值，即。截断奇异值就是只保留前面共k个较大的奇异值，截掉后面较小的奇异值，截掉的奇异值直接取零。则式(5)未知参数的TSVD 正则解为：

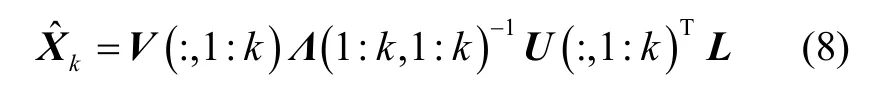
式中采用了matlab 形式的子矩阵表示方法，

Tikhonov正则化方法实质是用相邻的适定解去逼近原问题的解，通过构造稳定泛函准则并引入正则化参数来求解稳定的参数估值。对式(5)引入Tikhonov正则化算法，其正则化准则为：

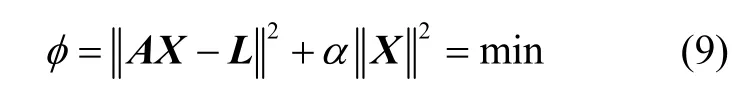
正则化解为：

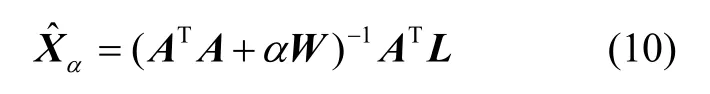
式中，α为正则化参数，根据观测数据受干扰程度确定α取值，随噪声由弱变强，α取值相应由小增大；W为对角矩阵，其对角元素为等效源的体积权重，若设计的等效源单元体的体积相同，则可取为单位阵。由此可见，相对于最小二乘估计，Tikhonov正则化估计是通过适当地牺牲了待估参数的有偏性来换取方差的减小。

比较TSVD和Tikhonov这两种正则化方法可以发现，二者在本质上是一致的，基本思路都是如何消除小奇异值的影响。二者的差异在于减少小奇异值对解的影响的程度上，TSVD 方法是直接抛弃了较小的奇异值对解的影响，相当于删除引起病态矩阵中不可靠的部分，而Tikhonov 正则化则是对矩阵进行约束，降低奇异值对结果的影响。

1.2.2 正则化参数的选取

对于TSVD 法，如何选择截断参数k是整个奇异值截断法的关键，而Tikhonov 正则化法需要确定合理的正则化参数α。本文将k和α统称为正则化参数，对于正则化参数的优选，有L 曲线法和广义交叉验证法GCV。

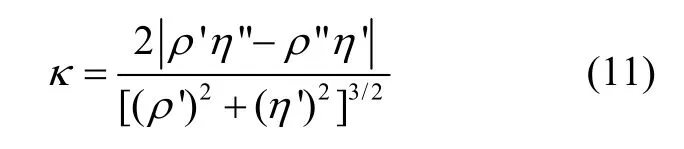
采用GCV 选择最佳正则化参数，就是选择一个参数值，使得GCV 函数最小：

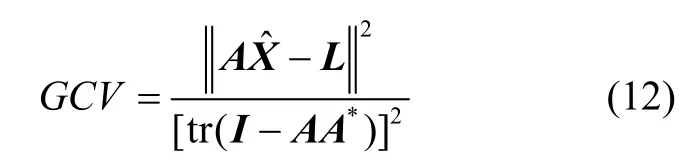
2 数值模拟试验

全张量梯度模拟。为了检验等效源降噪的效果，采用文献[9]的模拟实验，虚拟场源模型参数、模拟数据参数，均与文献[9]相同。采用文献[12]的无奇点公式正演计算得到空中80m飞行高度处的理论重力梯度值，将其作为真值，见图1 第1 列。图1 中从上到下分别是Txx、Txy、Txz、Tyy、Tyz和Tzz共6 个分量，每个梯度分量东西方向和南北方向均模拟了31个测点。然后在每个梯度分量上加上均值为0 E、标准差为5 E 的高斯白噪声，如图1 第2 列，可以看出噪声已经掩盖了信号。

部分张量梯度模拟。为了检验等效源转换重力梯度分量的效果，利用图1 第2 列中添加噪声后的Txy、Txx和Tyy这3 个分量模拟了FALCON 部分张量梯度测量系统的观测值——水平梯度分量和分量：

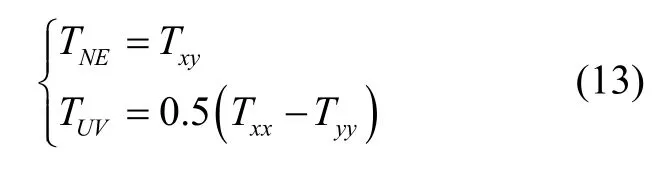
等效层设置。采用100 m 边长的立方体作为等效源，等效层的覆盖范围在每个方向上均超出数据区域5 个单位的等效源，因此等效层在东西和南北方向各有41 个等效源。等效层埋藏深度设置为贴近地面，即地下0～100 m。

方案1、基于L 曲线方法确定正则化参数的TSVD 方法，确定的截断参数k=229，如图2(a)；

方案2、基于GCV 方法确定截断参数的TSVD 方法，确定的截断参数k=193，如图2(b)；

方案3、基于L 曲线方法确定正则化参数的Tikhonov 正则化方法，确定的正则化参数α=0.015959，如图2(c)；

分别利用这4 种正则化方案确定出等效源模型的参数后，再重构重力梯度张量的6 个分量，并与无噪声的理论梯度值作比较，统计均方差如表1。从表1看出，4 种方案都能有效地提高滤波精度。综合来看，方案1 重构的重力梯度张量精度略高于其他3 种方案。尽管垂直梯度分量Tzz的精度有所提高，但效果不如其它分量，这也很好理解，重力梯度在垂直方向的量级较大，水平方向的量级较小，用较微弱的水平梯度信号来推算较强的垂直梯度信号，精度提升有限。图1 第3 列是采用FALCON 两个水平分量按照方案1 重构的重力梯度张量，从中看出，高频噪声被有效地滤掉了。

为了检验等效源模型对全张量重力梯度的降噪效果，将图1 第2 列的所有梯度分量作为观测值，采用方案1 的正则化等效源降噪，见图1 第4 列，精度统计见表1。从表1 看出，采用全张量重力梯度降噪，精度有大幅的提升，尤其是3 个直线梯度分量Txx、Tyy、Tzz的精度提升了50%以上。

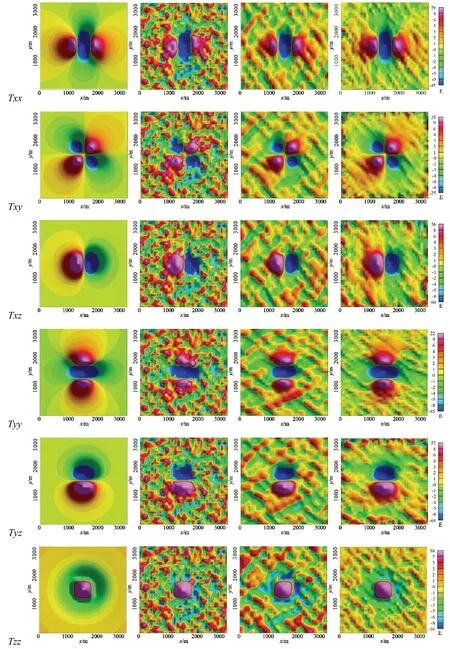
图1 重力梯度分量转换和全张量梯度降噪图 /EFig.1 Gravity Gradient Component Conversion and Total Tensor Gradient Denoising Diagram /E

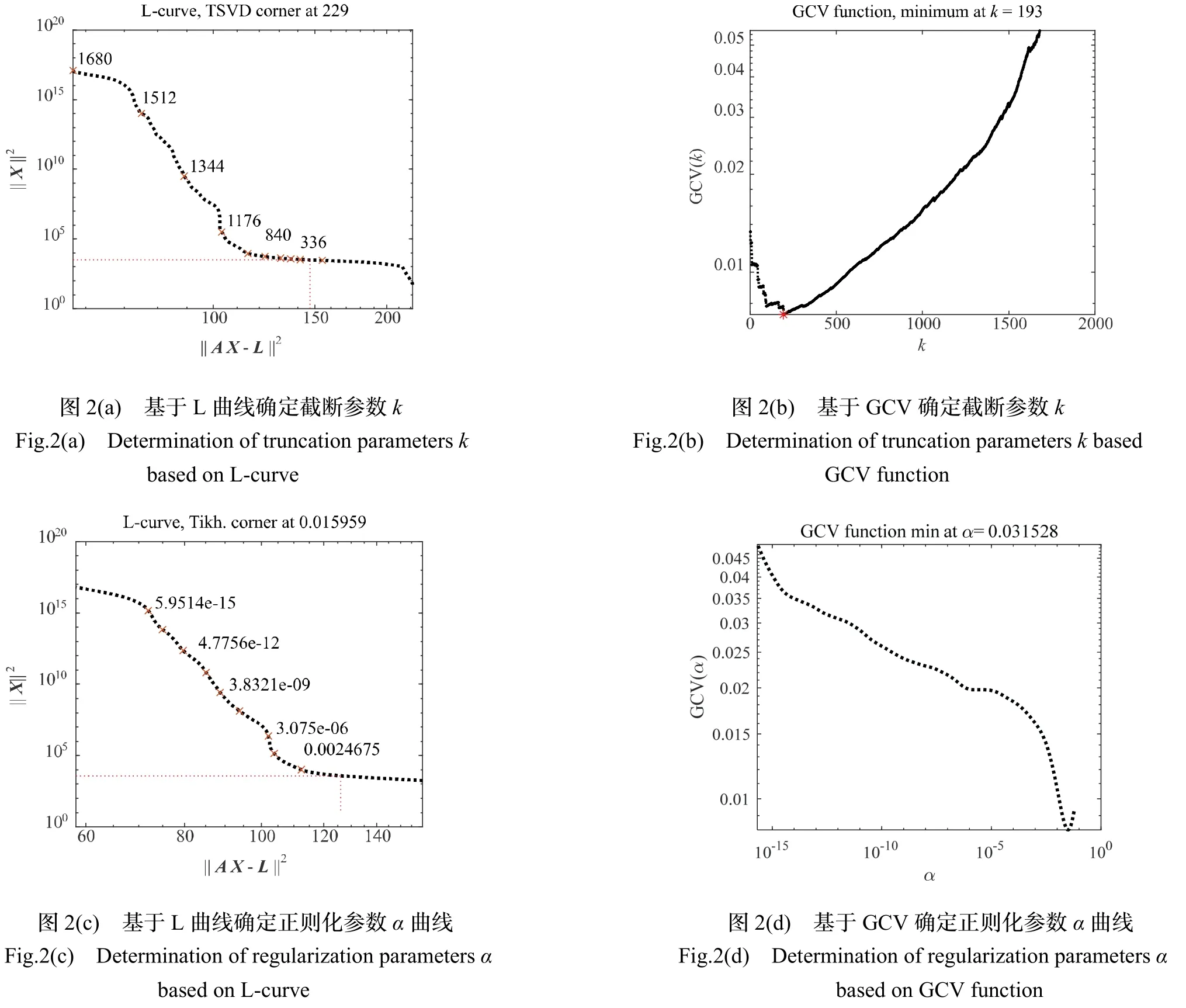
图2 正则化参数的确定Fig.2 Determination of Regularization Parameters

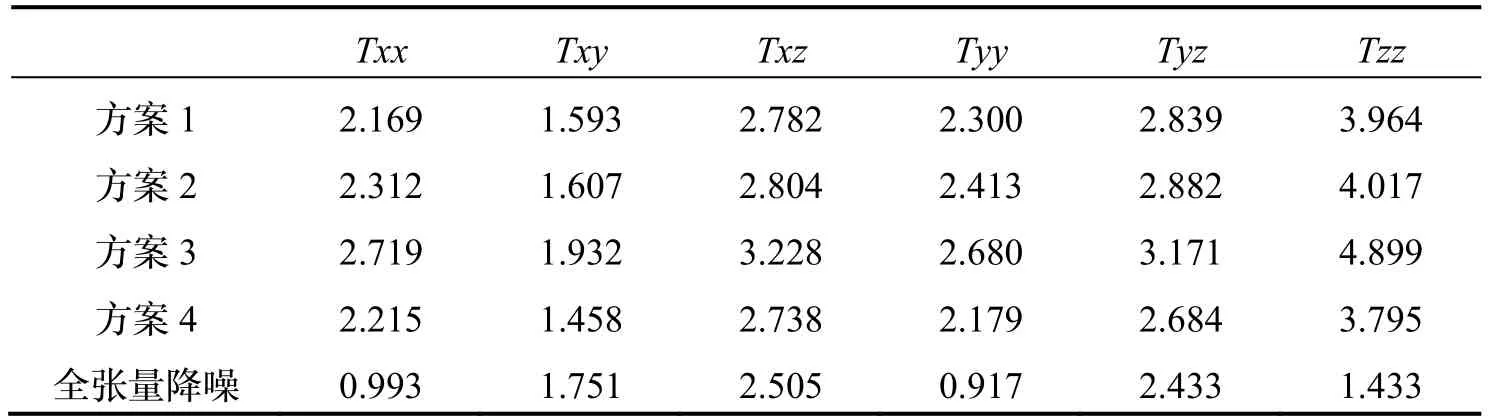
表1 不同方案降噪后的均方差（单位：E）Tab.1 Root mean square error of different noise reduction schemes（unit:E）

3 实测数据实验

FALCON 系统只能测量重力梯度的水平分量，但对实际应用而言，重力垂直梯度和重力异常具有更大的用处。因此，需要将水平梯度转换为垂直梯度和重力异常。为了检验等效源法滤波和转换的效果，采用HeliFALCON 实测数据进行转换试验。2014年，法国的通用地球物理公司 CGG（Compagnie Généralede Géophysique）公司承接了美国地质勘探局USGS 的合同，采用搭载于直升飞机的HeliFALCON系统在美国密苏里州苏利文北部开展了航空重力梯度和地磁测量。测区中心坐标为北纬38 °09 ′，西经91 °13 ′。直升飞机贴地飞行，平均飞行高度为90 m，测线为南北向，切割线为东西向，测线间距400 m，切割线间距4000 m，数据采样间隔约5 m，共获得了3537.7 公里的测线数据。

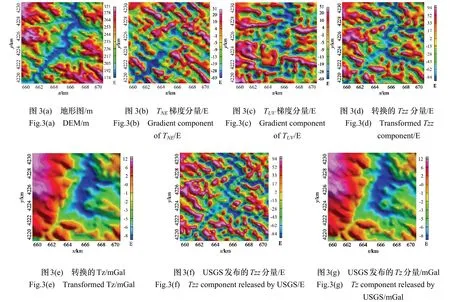
图3 重力梯度分量转换图 /EFig.3 Gravity Gradient Component Conversion Diagram /E

等效源法计算量大，因此提取一块10 km×10 km的范围做实验。将测线数据按通用横轴墨卡托UTM投影到平面上，然后采用最小曲率内插法，将原始离散数据网格化为100 m 间距的网格。实际上，等效源法可直接对原始点位上的观测数据进行计算，既不要求观测数据分布在水平面上，也不需要规则网格。这里将离散数据网格化，是为了方便绘图展示。图3(a)是直升飞机激光测高获取的试验区数字地形图，图3(b)是获取的TNE重力梯度分量，图3(c)是获取的TUV重力梯度分量，图中坐标单位均是km。

采用100 m 边长的立方体作为等效源，等效层设置在平均地形高处。基于L曲线法的TSVD 正则化方法，联合TNE和TUV两个水平梯度分量重构垂直梯度分量Tzz（图3(d)）和重力异常Tz（图3(e)）。Tzz展示的是地质体密度变化的俯视图，所以图3(d)和图3(a)形态上相似。Tz含有相对低频的波长信息，所以相对于Tzz图像更光滑。

USGS 发布了其采用频域位场转换方法计算的垂直分量Tzz（图3(f)）和重力异常Tz（图3(g)），该方法利用重力梯度分量在频率的内在转换关系，联合TNE和TUV两个分量采用傅里叶变换得到重力梯度的频谱[13]。

对比图3(d)和图3(f)，以及图3(e)和图3(g)，两种方法计算的Tzz和Tz形态基本一致，但是细节上还存在一些差异。USGS 采用的频域位场转换方法会导致噪声放大，因此该算法附加了一个低通滤波器以压制噪声。

用等效源法计算的Tzz和Tz分别减去USGS 公布的Tzz和Tz，统计二者的差异，如表2所示。

表2 等效源转换结果同USGS 转换结果差异统计表Tab.2 Statistical table of differences between equivalent source conversion results and USGS conversion results

Tzz平均差异为0.45 E，标准差为2.68 E，Tz平均差异为-0.14 mGal，标准差为0.36 mGal，表明等效源法滤波转换结果与UGGS 的结果吻合。

4 结论

利用矩形棱柱体正演重力梯度全张量的解析模型，构建了重力场梯度与等效源密度参数的线性方程组。构造的系数矩阵只与采样点坐标和等效源节点坐标有关，因此观测数据不依赖于平面网格化数据，可避免曲化平以及网格化引入的误差。针对虚拟等效源解算过程可能存在欠适定性的问题，引入截断奇异值TSVD 和Tikhonov 正则化方法。通过模拟和实测数据实验得出结论：

（1）等效源降噪能保证各梯度分量之间的内在联系。联合多个梯度分量能反演自洽的等效源参数，能确保不同梯度分量的同源性，能确保降噪后的梯度分量满足拉普拉斯约束；

（2）等效源法具有不同梯度分量之间转换的功能。通过梯度分量观测值反演等效源参数后，再利用梯度张量与等效源的解析模型，可以计算其它梯度分量，实现不同梯度分量之间的转换。该功能对于类似FALCON 这种只能获取水平重力梯度的系统来说，尤为重要，因为可以将水平梯度转换成垂直梯度和重力异常；

（3）正则化算法能有效改善等效源反演的稳定性和精度。模拟实验充分验证了正则化算法能降低病态方程系数矩阵的特征值对观测噪声的敏感度，有效抑制观测噪声的放大效应，提高了未知参数的稳定性和精度。综合而言，基于L曲线方法确定正则化参数的TSVD 方法精度较高。