基于AHDE和手机陀螺仪的行人航向修正方法
2021-05-27刘寒烁盛方园
郭 英,刘寒烁,叶 瑾,盛方园
(山东科技大学 测绘与空间信息学院,青岛266590)
近年来,位置服务成为了人们日常生活中必不可少的服务,全球卫星导航系统(Global Navigation Satellite System,GNSS)在位置服务中占据着重要的位置,然而导航卫星信号的可用性在室内不能得到保证,GNSS 在室内环境中的性能严重下降。因此,建立一个准确、可靠、实时的室内定位系统,满足公众的室内定位需求具有重要意义[1]。
随着微机电技术(Micro-Electro-Mechanical Systems,MEMS)的不断发展,惯性测量单元(Inertial Measurement Units,IMU)的体积越来越小,价格越来越便宜,并且随着智能手机的普及和改进,IMU 被普遍应用于智能手机中,使基于智能手机的行人导航定位成为室内定位领域的一个重要新分支[2]。
然而普通的IMU 均存在一定程度的累积误差影响,为了在误差影响下提高行人航向估算精度,国内外学者提出了一些航向修正方法:Borenstein 等人[3]提出了基于陀螺仪航向估计的启发式漂移消除算法(Heuristic Drift Elimination,HDE),该方法利用室内环境大多为矩形,走廊一般为直线型的特性,预先设定好四个主导方向,当检测到行人靠近主导方向行走时,航向偏差会由HDE 算法来修正;Jimenez 等人[4]提出了改进的启发式漂移消除算法(improved Heuristic Drift Elimination,iHDE),该方法在HDE 算法原有的主导方向上再加入四个,每个主导方向相隔45 °,相较于HDE 算法,iHDE 算法在非理想的室内环境中的表现要优于HDE 算法[5]。为了进一步提高航向估算精度,一些基于固定式IMU 的航向修正算法被提出。Muhammad 等人[6]提出了骨盆旋转-零速率更新旋转检测算法(Pelvic Rotation-ZUPT Turn Detection,PZTD),该算法基于腰部穿戴式惯性传感设备,检测行人是否直行和处于主导方向,对行人沿主导方向直行和未在主导方向直行两种情况进行航向修正,不仅对主导方向的航向修正也提高了非主导方向上的航向精度。王鹏宇等人[7]基于iHDE 算法,使用腰绑式惯性传感器,对航向建立缓冲区来抑制iHED 算法在特定场景下的过度修正问题。Ju 等人[12]提出了基于足绑式 IMU 的高级启发式漂移消除算法(Advanced Heuristic Drift Elimination,AHDE),该算法利用行人连续六步的位置数据判断是否直线行走或者沿主导方向直线行走。相比iHDE 算法,AHDE 加入了非主导方向直行的航向修正。在实际中,手机相较于固定式IMU 更加灵活,一些基于固定式IMU 的航向修正算法在手机端难以实现;室内环境复杂,非主导方向直行的情况较多,iHDE 算法难以发挥优势;室内直行的路线长短不一,AHDE 算法使用连续多步数据检测是否直行会直接影响计算效率和修正效果。
基于此,本文首先分析基于智能手机框架的互补滤波航向推算原理,然后根据一秒时域内航向变化幅度判断行人是否直行,针对直线行走和主导方向下直线行走建立航向修正算法,并且对行人停顿和姿态转换进行识别与处理,最后实验验证该方法在常规和复杂环境中的有效性。
1 基于互补滤波的航向推算基本原理
描述姿态常用的方法有欧拉角法、四元数法、罗德里格斯参数、方向余弦法等。四元数法相较于欧拉角法计算量大但计算精度更高[9]。而相较于罗德里格斯参数和方向余弦法,四元数法计算量小、简单高效,并且可以全姿态求解。而且四元数法避免了产生的奇点的问题[14]。因此这里使用四元数法来描述姿态,根据式(1)将初始欧拉角转换为四元数。
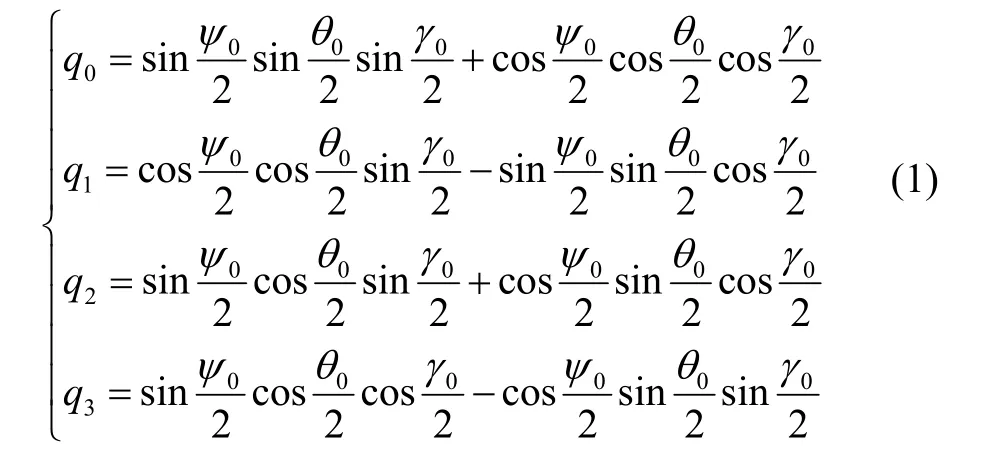
为了减弱陀螺仪漂移误差,提升航向推算精度,这里使用互补滤波融合陀螺仪和加速度计数据[10]。即通过四元数计算得到载体坐标系下的重力矢量其中为重力场在导航坐标系下的投影,单位为m/s2,为导航坐标系转换为载体坐标系的旋转矩阵;加速度计数据计算得到载体本身的重力矢量;实际上,也就是陀螺仪数据在一定程度上存在偏差,将上述两矢量叉乘得到偏差矢量e:

根据矢量偏差e及控制参数修正陀螺仪偏差:
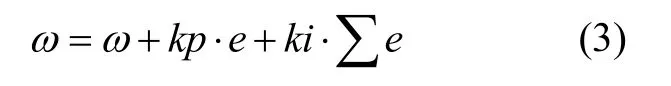
式中,kp为比例控制参数,ki为积分控制参数,ω为三轴陀螺仪数据。根据二阶龙格库塔法使用修正后的陀螺仪数据更新的四元数,并转换为姿态角。
2 基于高级启发式漂移消除算法(AHDE)航向修正方法
由于航向漂移误差会随着行走距离的增加不断增大,且行人在走路的过程中以直线行走居多,故有必要加入一定的航向修正算法。本文利用AHDE 算法中将行人行走状态分为非直线、直线、沿主导方向直线行走的思想建立航向修正算法。
2.1 AHDE 算法原理及分析
AHDE算法是由Ju等人[12]提出的高级HDE算法,该算法通过判别行人行走的方式将行人行走分为三种模式,即非直线行走、直线行走和沿着主导方向直线行走,改进了iHDE 算法缺少非主导方向直线行走时修正航向的问题[11]。在非直线行走时AHDE 算法不生效,误差与基于足绑式惯性单元 PDR 算法框架(INS-EKF-ZUPT,IEZ)一致[8];在直线行走时,将当前行进航向与五步前的航向作差,使用该差值作为扩展卡尔曼滤波(Extended Kalman Filter,EKF)的测量值估计航向;在沿着主导方向直线行走时,将当前航向与主导航向的差值作为EKF 的测量值估计航向。
相比较于HDE 算法,AHDE 算法不仅能在简单的主导方向上起到明显效果,而且能在复杂的路线上起到一定作用。而AHDE 算法应用于IEZ 框架中,在手机端不适用;AHDE 算法在判定行走状态时用到连续六步位置数据,由于步数较大,航向修正将会延迟[6];同时,AHDE 算法使用五步的位置数据估算直线行走的航向也会引起不必要的误差。而且,AHDE算法未考虑到主导方向偏离时过度修正问题。
2.2 航向修正算法改进
考虑到手机陀螺仪自身误差,这里以互补滤波推算得到的航向为输入值,按照时域分析航向角的变化情况判断是否直行;对直线行走的航向加入直线修正估算行人航向,而非使用第一步的航向值作为直线行走的航向;沿主导方向直线行走时加入直线和主导方向修正算法估算行人航向,将直线修正后的航向与主导方向的差值作为输入量估计行人航向;对非直线行走航向加入航向抖动检测及消弱算法,避免手机抖动过大引起的误判;最后对停顿点和姿态转换进行识别与处理,提高行人在复杂室内环境中的航向精度。
2.2.1 行走模式识别
传统的AHDE 算法中,确定直线行走所需要的步数相当大,导致检测滞后,引起不必要的延迟和误差。室内环境下直行路线长短不一,可能轨迹的末端是非主导方向,或者直行步数达不到检测所需步数,这种情况下航向修正效果可能更差。为了避免这种情况,通过式(4)计算航向变化幅度,通过记录航向和1 s 内航向变化幅度确定是否直行。

式中,m为1 s 窗口大小(在这里m=50),为历元i下的航向角,为历元i下的航向变化幅度。一些学者分析行人在走路的过程中盆腔最大旋转的幅度在4 °到9 °之间。在行人前进的过程中手持的手机会随之产生一定程度的抖动,如果按照最大旋转幅度来考虑行人在行走过程中的抖动情况,可以认为一步的航向变化在9 °内。
为了能更加准确的判别行人的行走模式,这里通过实验来验证行人行走时的航向变化幅度。实验地点为山东科技大学J6 楼,实验中使用的智能手机为OPPO R9s,该智能手机的惯性传感器为博世公司的BMI160,该传感器的部分参数见表1。

表1 BMI 160 传感器技术参数Tab.1 Specifications of the BMI 160
在实验中,我们招募了5 名志愿者覆盖了不同的年龄身高以及性别,其中包括男性A,175 cm/70 kg/50岁;男性 B,180 cm/90 kg/29 岁;女性 C,174 cm/63 kg/26 岁;男性D,167 cm/56 kg/16 岁;女性E,163 cm/58 kg/50 岁。志愿者被要求在40 m-100 m的直线中行走,传感器采样频率为50 Hz,实验中将手机平放在胸前,保持导航模式行走。为了直观展示航向变化幅度的分布情况,该部分数据以箱型图的形式展示,如图1所示,其中A1 和B1 为志愿者A 和B非匀速行走数据。在箱型图中,中心标记为数据中值,箱的上下端分别表示第25%和75%位的数据,“+”表示异常值。

图1 行人航向变化幅度箱型图Fig.1 The box-plot of change of pedestrians heading
从图1 和表2 可以看出,匀速行走下的航向变化幅度平均集中在3 °以下,即便是最大异常值仍在4 °以内;非匀速行走的数据是为了模拟直线行走过程中手机不平稳的情况,平均最大异常值在4.5 °左右,在非匀速A1 实验中超出了4.5 °,虽然在实验处理中将非连续性超出阈值的异常数据认作噪音去除掉,但也说明过度的航向抖动可能会引起误判,为减弱这一情况的影响,后续的航向修正会针对误判情况进行修正。根据盆腔旋转幅度以及实际直线行走的结果可以得出合适的判断直行的阈值DTh。
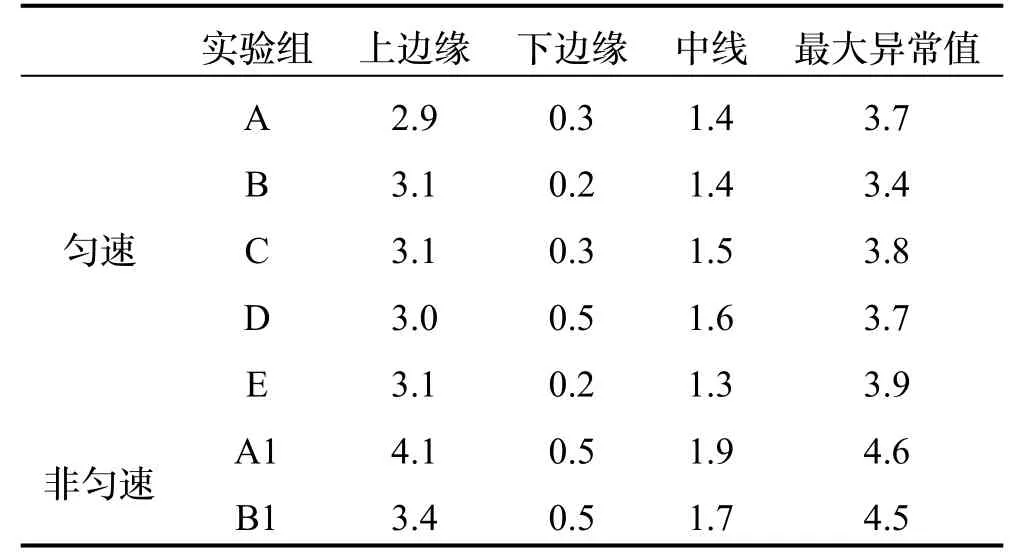
表2 行人航向变化幅度数据表(单位:(°))Tab.2 Table of pedestrian course change amplitude data(Unit:(°))
2.2.2 直线行走航向修正
传统的直线航向修正是在判断行人连续几步的航向变化不大的情况下,将后续的几步航向角与判断为直线行走起的航向保持一致,直至脱离直线行走。传统方法判定为直线行走时行人的航向是保持不变的(即,直到脱离直线行走),这与实际并不相符(行人直线行走时航向会小幅度波动)。为了降低直线行走过程中航向偏差,以及考虑到阈值判断时产生的误判情况,公式(5)将当前航向与直线方向的偏差作为输入量对直线行走模式下的航向偏差分等级修正,其修正示意图见图2。

图2 直线行走下航向修正对比图Fig.2 Comparison chart of heading correction when walking straight
其中小角度偏差被完全减弱,大角度偏差保留一定原有特性,若超出直线行走的正常航向变化范围,结束直线修正。这样不仅修正直线行走航向偏差而且降低误判造成的过度修正影响。
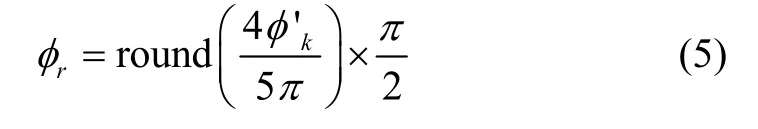
2.2.3 主导方向航向修正
主导方向是事先建立好的方向,如图3所示,当行人沿着主导方向直线行走时,航向被主导方向修正算法修正。

图3 主导方向示意图Fig.3 The chart of dominant direction
图3 将主导方向定为8 个,行人直线行走时的航向在主导方向附近时会被识别算法检测,式(6)[6]为主导方向判别公式。
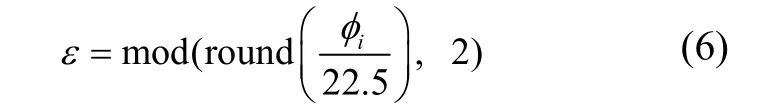
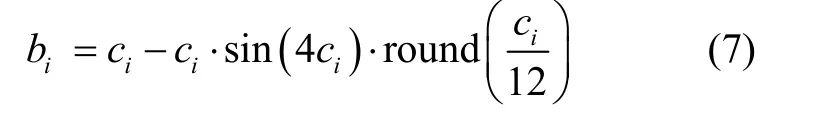
当前航向与主导航向偏差量ic为:
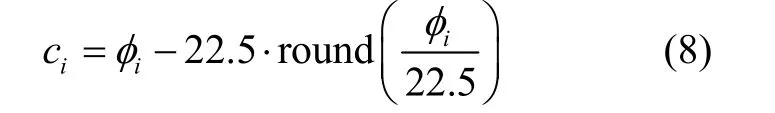
通过以上公式进行两圈矩形100 m 行走测试,如图4所示。互补滤波计算得到的航向偏差会随着时间不断变大,图中行走状态为1 则行人转弯;为0 则行人直行,可以看出行走模式能够被正确判断,航向偏差能够被检测并且被修正算法补偿。
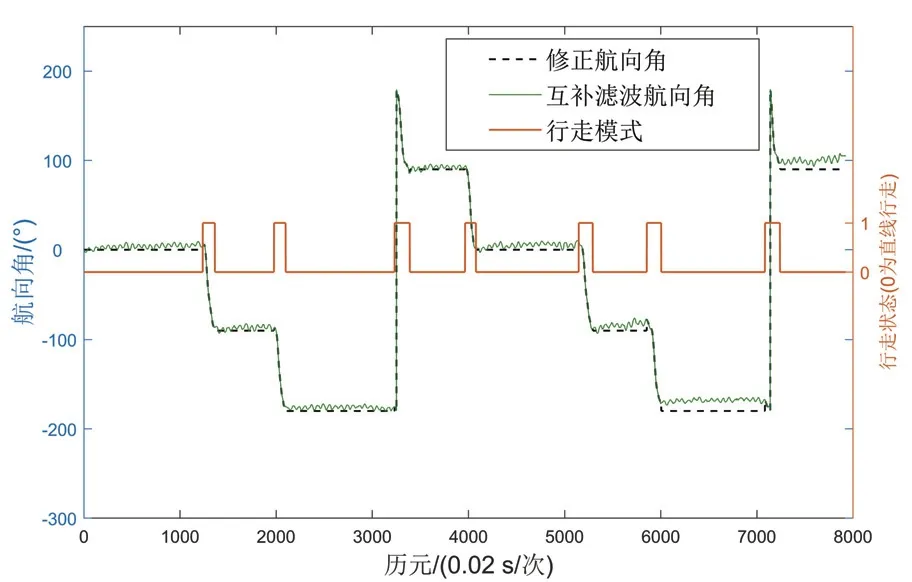
图4 主导方向直线行走航向修正对比图Fig.4 Heading correction comparison chart for straight walk along the dominant directions
2.2.4 航向抖动识别与减弱
考虑到在修正航向角的过程中可能因各种影响造成航向抖动导致直线行走未被正确识别,通过加权平均模型建立航向抖动减弱公式(9),该公式使用非直线行走下连续三步的航向数据来判断航向抖动情况,即连续三步航向相互作差,将抖动情况分为三类并分别修正,其修正示意图见图5。
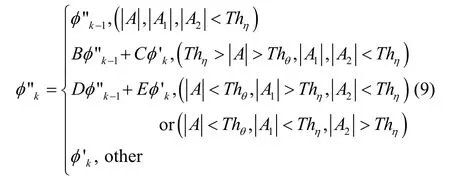
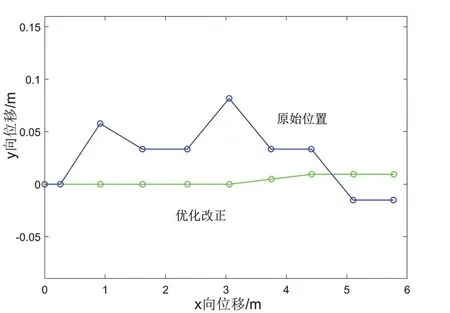
图5 航向抖动优化示意图Fig.5 The chart of heading jitter optimization
行人步频使用传统的峰值检测法计算,步幅模型为非线性模型中的Weinberg 方法[13],最后结合步长和航向信息推算行人航迹。
2.2.5 停顿点识别与处理
为了解决行人在行走的过程中遇到障碍物,或者因其他原因在原地停顿而产生位置误差的问题,在推算行人航向的同时加入了停顿点检测。
由于行人在某一位置停顿时加速度计数据趋于稳定,因此选择建立加速度数据方差识别行人的停顿位置。
图6(a)展示了手机在平放状态下行人停顿和行走时的加速度计数据,停顿状态下明显稳定于行走状态,从图6(b)可以看出根据其3 轴加速度计计算的窗口方差,在停顿区域的方差值十分稳定,相互配合可以比较准确地确定出停顿点的位置。

图6 停顿检测示意图Fig.6 The chart of pause detection
为此通过研究建立了行人停顿时的检测识别方法,如下式:
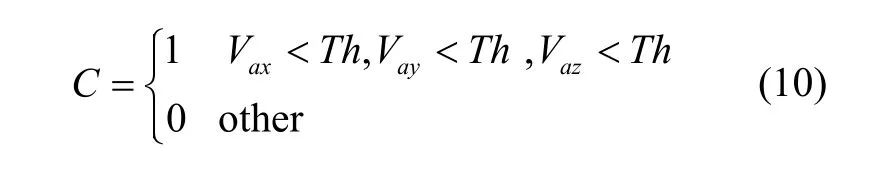
由于舍去停顿区间分段建立行走路线,需要匹配停顿区间前后的航向,选取停顿前短时间内未发生大幅度变化的四元数的均值,使用该四元数来推算下一段路线的行人航向。
2.2.6 手机姿态转换识别与处理
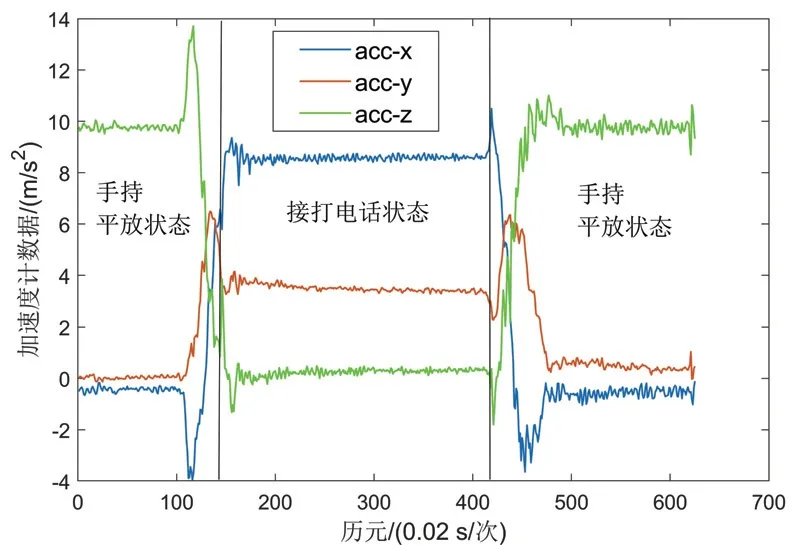
图7 不同手机位置下加速度数据对比图Fig.7 The chart of acceleration data in different mobile phone position
手机平放查阅及打电话模式之间的转换为手机导航常见的姿态转换,所以这里主要研究行人在行走的过程中手机的手持姿态和打电话姿态转换的情况。
由于手机的平放姿态和打电话状态时的倾斜角度完全不同,因此三轴加速度计的大小就会根据姿态转换发生变化,如图7所示,接打电话状态和手持平放状态下的加速度计数据有着显著的区别,根据这种变化判断是否在打电话。
在姿态转换过程结束以后的三轴加速度计和陀螺仪数据难以计算真实的行走航向和步长,为了得到真实的航向数据和步长数据,采用旋转矩阵的方法进行数据转换,将加速度计数据和陀螺仪数据恢复到手机平放状态下。公式如下:
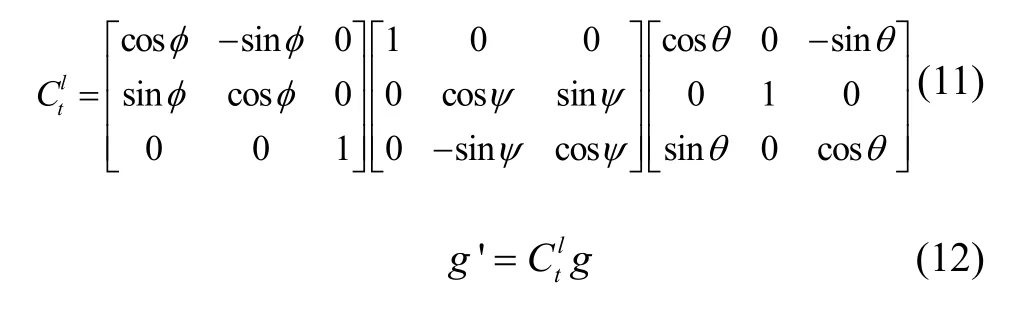
式中,φ为在转化到打电话前一时刻的手机航向,ψ和β是在打电话状态下的手机俯仰角和横滚角,建立得到的即为在行人打电话状态下相对于手机平放状态的旋转矩阵,'g为修正后的三轴陀螺仪数据,g为原始三轴陀螺仪数据。通过旋转矩阵将打电话状态下的加速度计和陀螺仪数据转换到手机导航坐标系下,进而推算真实行人航向。
3 实验分析
为了验证本文提出算法的有效性与可靠性,针对不同的行走情况采集了多种路线下的数据进行对比,其中包括了常规性路线,以及针对特定情况的复杂性实验,对实验数据分别使用改进的航向修正算法以及互补滤波算法。使用闭合差、点位误差、航向误差综合比较实验的精度,最后对各组实验路线全长相对闭合差进行比较。
3.1 常规实验
常规性实验包括96 m 矩形行走路线实验和主导方向偏离实验,实验过程中均保持手机平放在胸前,该部分实验可以直观地反映出航向修正算法在主导方向直线行走时的航向纠正能力,以及偏离主导方向时的避免修正过度能力。
在矩形行走路线中,行人在主导方向直线行走,通过改进的航向修正算法修正后的航向以及路线都有着明显的精度提升,如图8所示。航向修正后的平均航向误差为0.1 °,相较于PDR 互补滤波算法航向精度提高97%,其相对闭合差为0.1%,精度提升94%(见表3 和表5)。
主导方向偏离误差测试实验旨在检测主导方向修正算法是否会过度修正主导方向边缘的航向。实验路线为先直线行走,经过两个90 °转弯,然后转向靠近主导方向的方向直行回到原点。由于前半段沿着主导方向行走,航向偏差能够被正确补偿,后半段沿着主导方向边缘行走,航向修正算法被干扰,如图9所示,但航向修正算法精度仍优于PDR 互补滤波算法。其中航向修正算法的平均航向误差为0.7 °,相对闭合差为0.2%D,精度提升71%(见表3 和表5)。
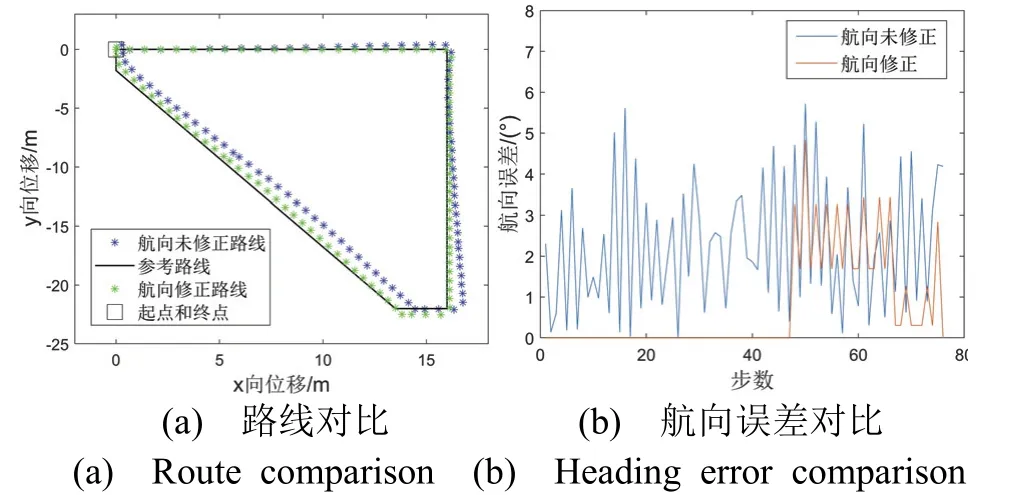
图9 主导方向偏离实验对比图Fig.9 The comparison chart of dominant direction deviation experiment

表3 航向误差对比表Tab.3 The comparison table of heading error
3.2 停顿实验
停顿实验包含三角形行走实验,以及含有曲线的矩形行走实验,实验过程中手机平放于胸前,两个实验中均包含了停顿点。
在三角形行走实验中,无论是否沿主导方向直行均能发挥出航向修正算法的优势,如图10(a)所示,并且点位精度优于互补滤波算法,如图10(b)所示。航向修正算法的平均点位误差为0.1 m,精度提升77%;相对闭合差为0.7%D,较与未修正航向路线精度提升71%(见表4 和表5)。
带有曲线的停顿实验中包含了直线和曲线行走,体现航向修正算法在含有曲线行走的路线中同样有效,避免因识别错误或者过度修正而导致严重误差。实验中PDR 互补滤波算法的路线产生了偏移,如图11(a)所示。航向修正后的路线平均点位误差为0.03 m,精度提升95%;相对闭合差为0.7%D,精度提升22%(见表4 和表5)。
未加入停顿识别处理算法的路线均在停顿后出现较大的位置偏差,其中三角形路线闭合差为4.39 m,带有圆形路线闭合差为1.95 m。
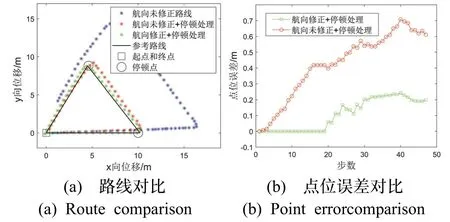
图10 带有停顿点的三角形路线对比分析图Fig.10 The comparison chart of triangular route with paused point
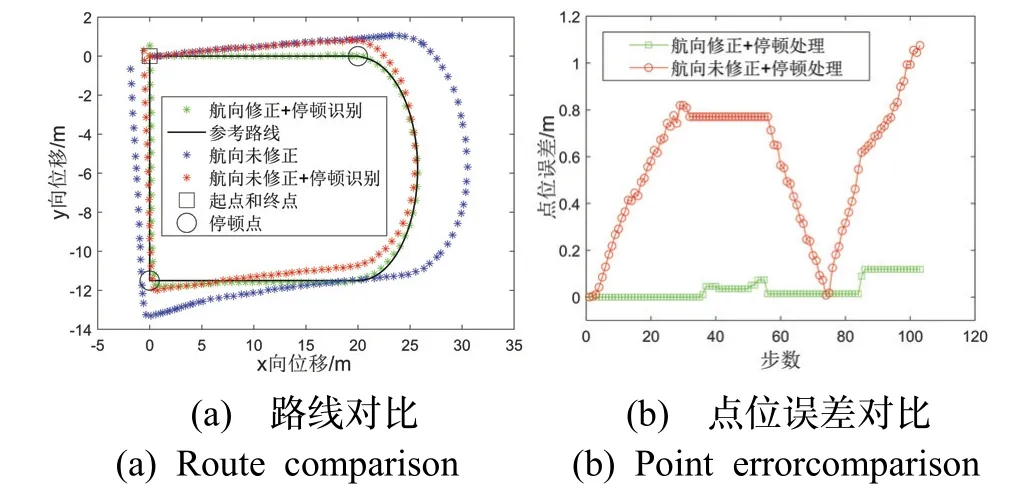
图11 带有停顿点和曲线路线的实验路线对比分析图Fig.11 The comparison chart of experiment route with paused point and curve route
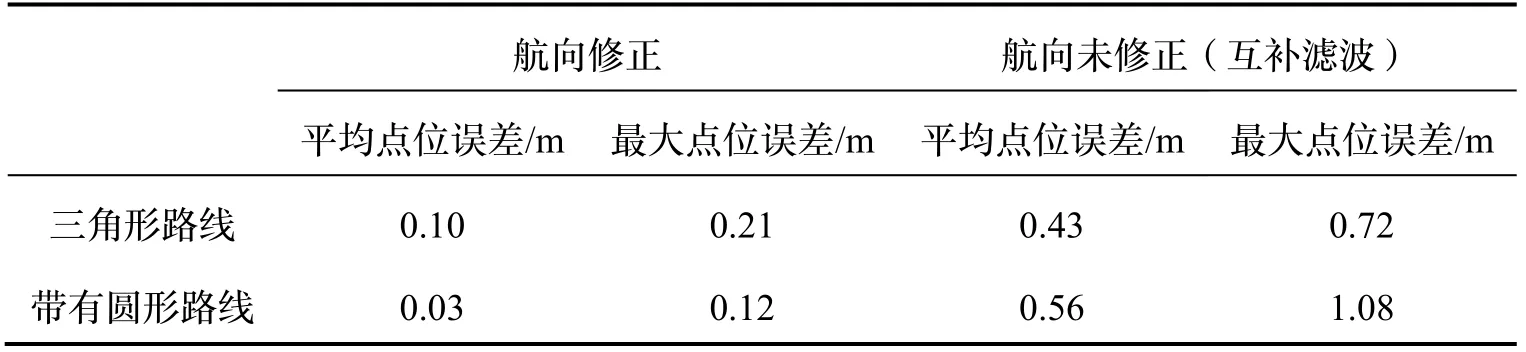
表4 点位误差对比表Tab.4 The comparison table of point error
3.3 姿态转换实验
该部分实验包含了姿态转换和停顿检测的内容,路线为多个转弯的行走路线,整个过程先从手持平放状态转换为打电话状态,中途停顿三次,再转换为手持平放状态直到终点,路线对比图如图12所示。
未加入停顿识别算法和姿态转换算法的解算路线出现了严重的误差;由于路线较短、手机抖动较小等原因PDR 互补滤波算法也起到了良好的修正作用,但仍然有一定程度的航偏。经过航向修正的路线相对闭合差为0.7%D,相较于PDR 互补滤波算法提升了60%。姿态转换实验中未处理停顿点的路线闭合差为5.9 m,未处理姿态转换和停顿点的路线闭合差为21.7 m。
为了更直观地比较航向修正算法对位置精度的影响,表5 对比了上述实验各种路线的闭合差以及路线 全长相对闭合差。两种算法均加入姿态转换处理与停顿处理,因而不包含停顿识别和姿态转换带来的误差。
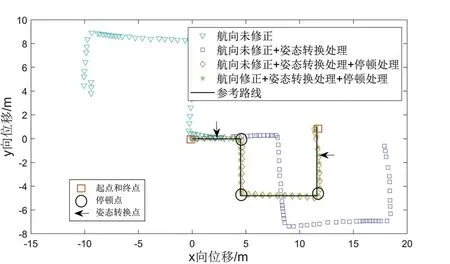
图12 带有姿态转换和停顿点的实验路线对比图Fig.12 The comparison chart of experiment route with attitude change and paused point
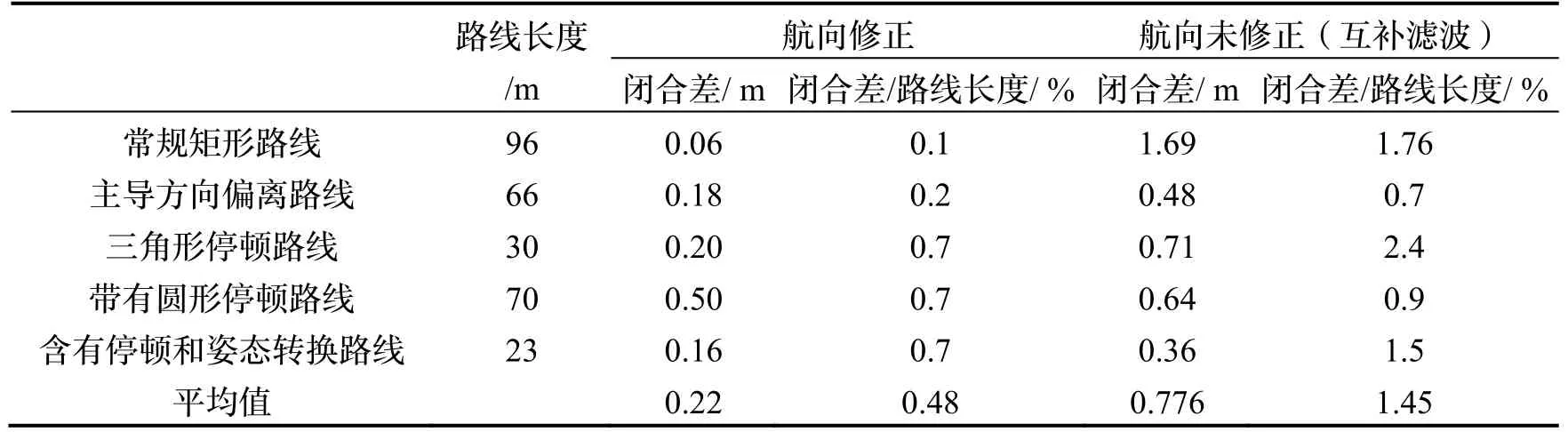
表5 各实验位置精度分析表Tab.5 Position accuracy analysis table for each experiment
4 结论
本文分析当前航向修正算法HDE、iHDE 以及AHDE 的特点和优势,在此基础上建立改进的航向修正算法,针对航向漂移、航向抖动、行人停顿和姿态转换引起的误差,分别建立识别和修正模型。结合多种行走路线以及行人行走状态实验,结果表明:
(1)互补滤波算法在短距离内能够起到一定的效果,但其航向误差会随着距离的增加不断增加,而航向修正算法能够一定程度消除陀螺仪漂移偏差,在本文实验中,不同的环境中的航向修正后路线相对闭合差范围为0.1%~0.7%,相较于互补滤波算法精度提升范围为22%~94%,平均提升68%。
(2)停顿识别与消除算法能够有效处理行人停顿问题,本文的实验中加入该算法的行人停顿行走路线闭合差精度提高范围为80%~96%。
(3)综合路线包含了航向修正、停顿识别及处理和姿态转换内容,本文综合路线闭合差精度提高范围为50%~98%。实验表明本文研究内容在三种方法相互配合的复杂行走状态路线下保持良好的精度和稳定性。
本文研究的算法在主导方向边缘时修正能力会受到影响,航向修正算法的优势受到限制,接下来的研究会考虑改进主导方向边缘修正精度以及加入磁力计来提升定位精度。
