基于IEKF的水下无人潜器无源动基座自对准方法
2021-05-27黄凤荣邢路然陈英姝朱雨晨
黄凤荣,邢路然,陈英姝,王 震,朱雨晨
(河北工业大学 机械工程学院,天津 300401)
初始对准是惯性导航系统进行导航的前提,初始对准的精度将直接影响系统的导航精度。水下潜器(Autonomous Underwater Vehicle,AUV)在被母船投放之前,受限于实际安装使用环境和舰船新旧电气设备链接的困难,传递对准很难实施,这要求AUV 必须具备在航行过程中实现自主初始对准的功能;也就是在装订大概的速度信息和初始航向角,甚至在没有装订初始航行角条件下尽快完成动基座初始对准。在这种条件下,惯性导航系统完成自对准的主要难点是:首先,由于外界行驶环境和自身运动影响,载体的速度不可能与装订的速度完全一致,因而速度是不准确的,这将导致初始对准常用的卡尔曼滤波收敛精度降低,甚至发散;特别是,惯性导航系统在运动过程中系统的误差模型是非线性的,系统需要在大失准角的情况下,实现初始对准。
近年来非线性系统状态估计在惯性导航领域的组合导航、初始对准等方面受到广泛关注,包括扩展卡尔曼滤波(Extended Kalman Filter,EKF)、无迹卡尔曼滤波(Unscented Kalman Filter,UKF)、粒子滤波(Particle Filter,PF)等[1-6]。其中,传统的EKF 有两个主要缺陷,首先EKF 对系统状态初值的准确性要求很高,如果状态初值设定的与实际情况差距较大,滤波器很难收敛;其次EKF 还会导致不一致性问题,即每当新的观测到来时,EKF 会通过旧状态的线性化来计算当前状态的协方差矩阵,但是当前状态协方差矩阵的实际值并不与其保持一致。UKF 相较于EKF 来说,实用性更强,但传统的UKF 和EKF 都需要已知系统噪声和量测噪声的先验统计,在实际应用中,由于各种环境限制以及算法本身存在的问题,必然会导致滤波精度下降,甚至发散[7,8]。
针对水下潜器惯性导航系统动基座初始对准的难点,本文通过分析水下潜器惯导系统误差特性,建立捷联惯性导航系统(Strapdown Inertial Navigation System,SINS)模型,设计系统在大失准角下的不变扩展卡尔曼滤波(Invariant Extended Kalman Filter,IEKF)初始对准算法,从而克服外界参考信息不准确以及存在扰动的情况。IEKF 基于李代数将群变换应用于状态变量,改变误差的定义方式,实现系统矩阵与状态估计值的独立,扩展了保证状态和协方差收敛的状态空间[9,10],解决了EKF 存在的问题。跑车试验证明,该方法在大方位失准角的情况下,航向角在30 min内快速收敛到1 mil 以内,证明了该方法的有效性和可行性。
1 不变扩展卡尔曼滤波
假设有如下形式的非线性离散系统:
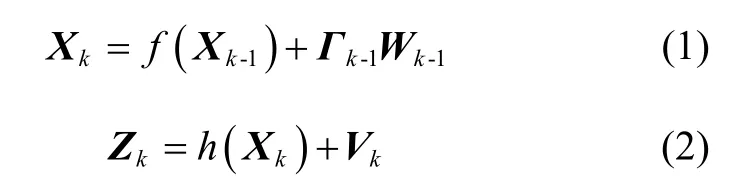
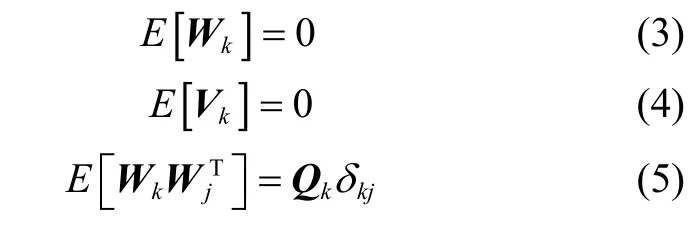
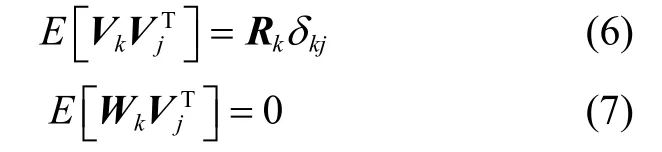
1.1 扩展卡尔曼滤波
传统卡尔曼滤波是在标准条件下推导而来的,是一种无偏的线性最小方差估计算法,同时对系统要求严格,仅适用于系统模型准确、噪声统计特性已知的线性系统。但在实际应用过程中由于外部运动的不规律和惯性元件的随机误差,在动态运动中很难得到系统精确的数学模型和噪声统计特性[11],系统本质上是非线性的,这将导致滤波器精度降低甚至滤波发散的现象。扩展卡尔曼滤波通过进行泰勒级数展开,略去高阶项,将非线性系统近似为线性系统,再作线性卡尔曼滤波估计,解决了标准卡尔曼滤波仅适用于线性系统的问题。
EKF 递推公式为:
状态预测值:
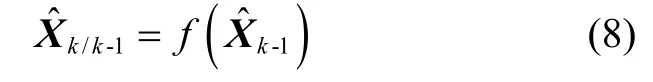
相关协方差:
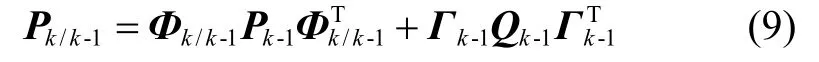
滤波增益:
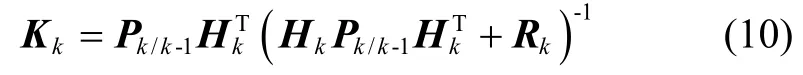
状态更新:
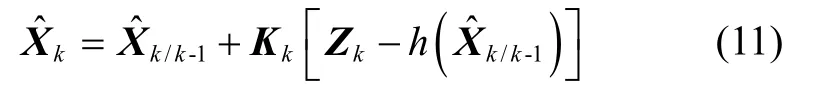
协方差更新:
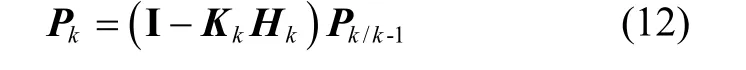
其中,I 为n 阶单位阵。
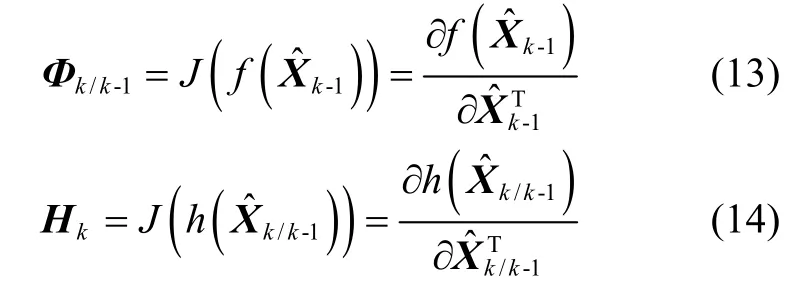
1.2 不变扩展卡尔曼滤波
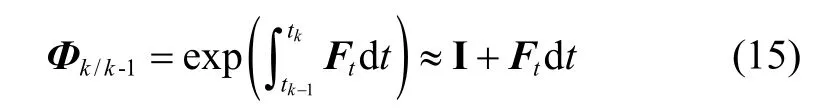
为解决上述问题,IEKF 基于李代数,将群变换应用于系统状态变量,所以IEKF 的状态量是一个矩阵,并且构成群。为了实现系统矩阵与状态估计值的独立,解决传统EKF 存在的问题,将误差也定义在群上,即下面左不变误差和右不变误差两种形式:
1)左不变误差

2)右不变误差

选择左不变误差还是右不变误差的依据是能否实现系统矩阵与状态估计值的独立。本文使用右不变误差建立SINS 模型。在此误差定义下,IEKF 的系统矩阵为常值,与当前状态估计值以及输入均无关,因此解决了上述EKF 存在的正反馈与不一致性问题。
2 水下无人潜器IEKF 滤波模型
为了解决水下无人潜器在没有准确外参考信息条件下的惯导系统动基座自对准问题,本文提出基于不变扩展卡尔曼滤波的动基座自对准方法。首先选取SINS 的方向余弦矩阵速度位置,陀螺和加速度计的随机游走偏差作为状态变量,建立系统状态方程;其次选取SINS 解算速度与用解算航向角分解的外参考速度之差作为量测信息构建量测方程;同时构建IEKF 滤波模型,设计滤波算法,实现了水下无人潜器的无源动基座自对准。
2.1 惯性测量单元模型
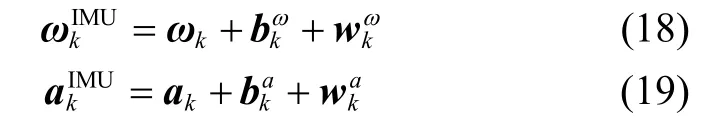
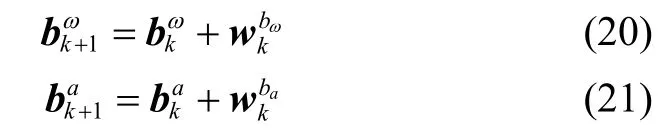
2.2 系统模型
载体的动力学模型如下:
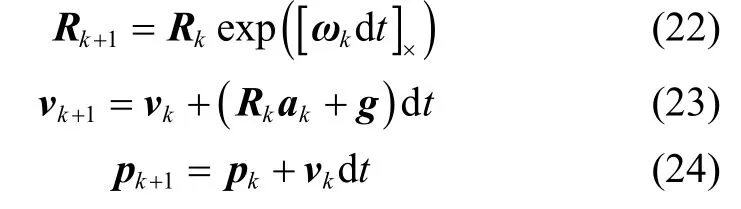
当考虑IMU 的随机游走偏差时,IEKF 系统模型的状态量分为可被描述成群元素的量,和不能被描述为群元素的量即:

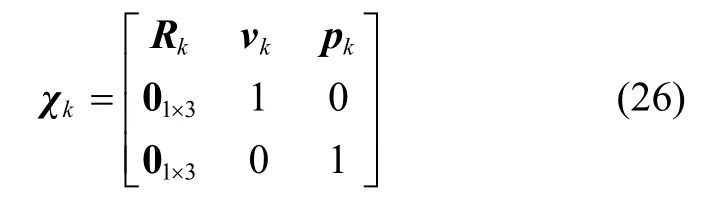
增广右不变误差定义为:
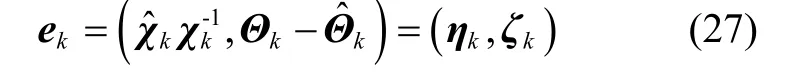
其中,
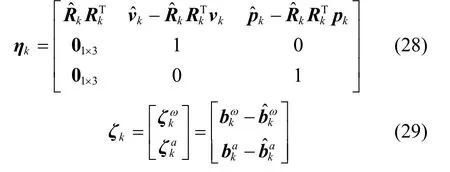
其中令:
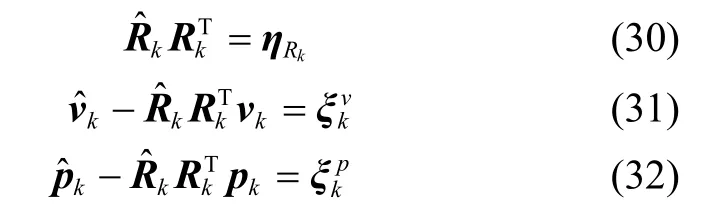
要想得到系统状态方程,首先需要对增广右不变误差式(27)对时间进行微分,即:

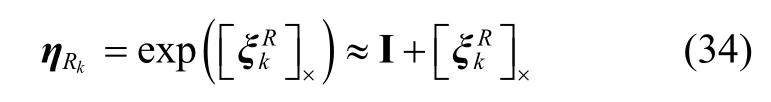
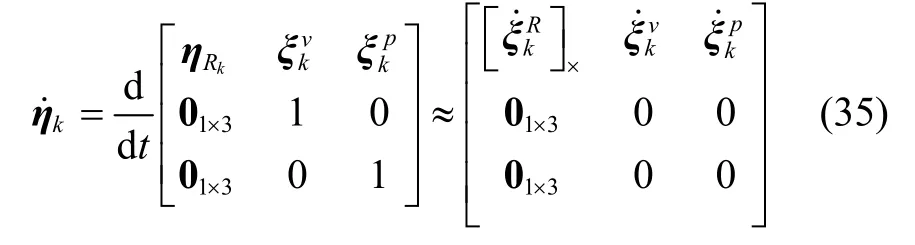
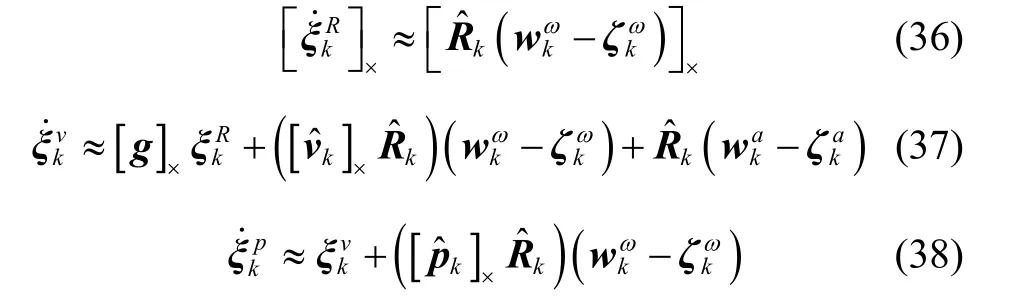
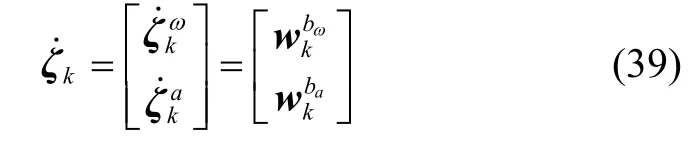
综上,系统状态方程为:
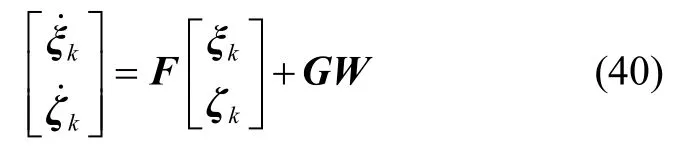
其中,
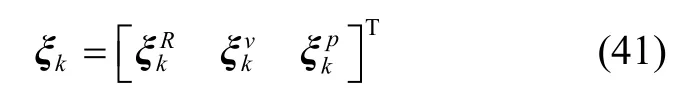
F为系统矩阵,G是噪声输入矩阵。
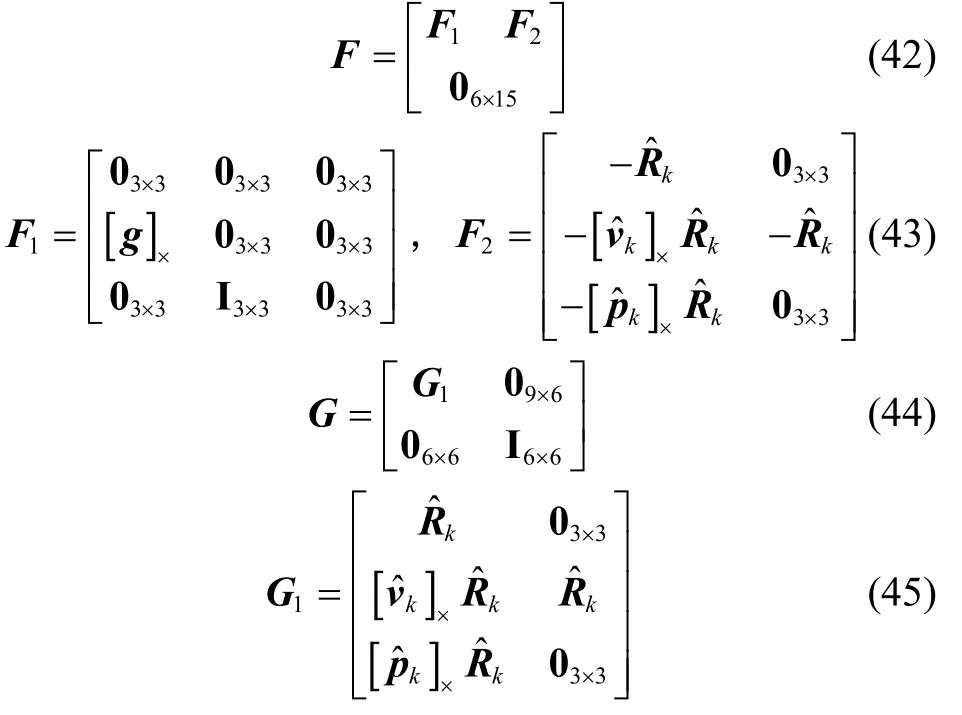
从式(42)(43)可以看出,在不考虑陀螺和加速度计偏差的情况下,系统矩阵为,与当前状态估计值和输入均无关,是一个常值。正是因为这一特点,IEKF解决了传统EKF 存在的正反馈和不一致性问题。
而在考虑IMU 的偏差时,系统矩阵F不再是一个常量,每个时刻的系统矩阵与当前状态估计值有关。但是这种联系只通过惯性元件偏差或噪声等小量引入,对于这样的系统方程[12],仍然能够保证一致性,同样在鲁棒性和收敛性上优于传统的EKF。
2.3 观测模型
初始对准过程中航向信息的可观测度较弱,特别是在运动过程中外界提供速度信息不稳定情况下。在采用速度误差作为观测量时,考虑航向信息的融合,在计算惯导系统北向和东向速度时,用导航解算的航向角对外参考速度进行分解。
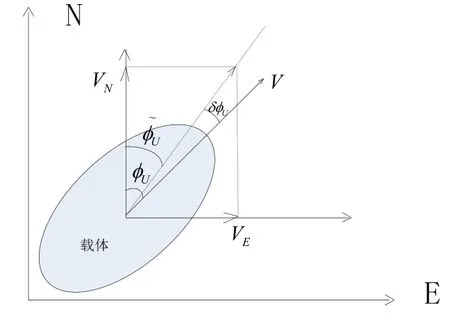
图1 合速度分解示意图Fig.1 Resolution of resultant velocity
设合速度为V,航向角为,则系统的速度分解公式可以表达为:
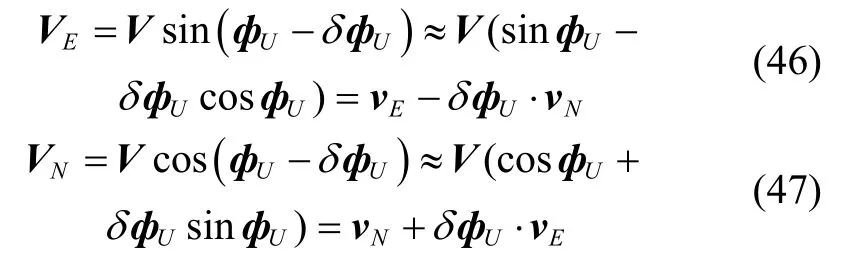
量测方程:
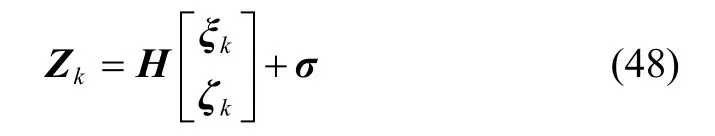
其中,σ为观测噪声。
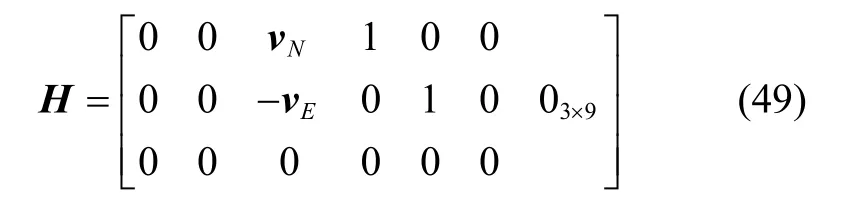
2.4 算法流程
IEKF 算法的流程与传统EKF 相同,只是状态更新公式不同,即:
设线性化的状态误差为,
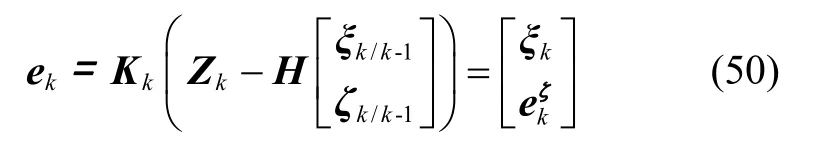
可得状态更新公式,
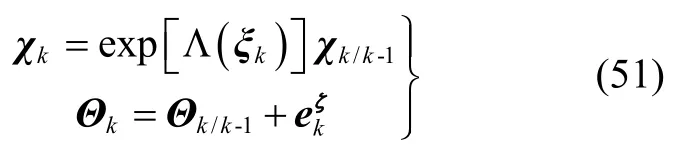
其中
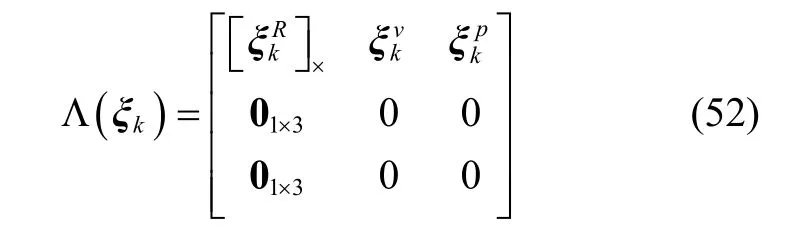
如式(51)所示,IEKF 中能表示为群元素的部分采用指数更新,不能表示为群元素的部分采用普通的线性更新。
3 试验验证
为了验证基于IEKF 水下无人潜器无源动基座自对准算法的可行性与工程实用性,进行了跑车试验。试验设备采用光纤陀螺捷联惯性导航系统,其中光纤陀螺零偏稳定性为0.01 °/h,加速度计零偏稳定性为50 μg。同时将一套高精度惯导系统作为基准设备,以验证IEKF 方法的性能。试验中同时同步录取基准设备以及试验设备的信息。
在试验过程中,待试验车基本在匀速运动状态稳定后,将光纤捷联惯导系统通电,根据实际车速人工装订一个固定的速度。本次试验装订速度为6.5 kn,保持车辆匀速运动,半小时后完成初始对准,同时同步录取基准设备的导航信息进行对比。
在载体匀速运动过程中,由于开车人员或道路条件的外界因素影响较大,载体的速度很难保证精确地按照设定的速度(6.5 kn)匀速运动。在这种情况下首先将IEKF 估计出来的速度与GPS 速度进行对比,如图2所示。由图2 可以看出,设计的IEKF 滤波器能在速度波动的时候有效地跟踪实际速度,保证了对准精度。
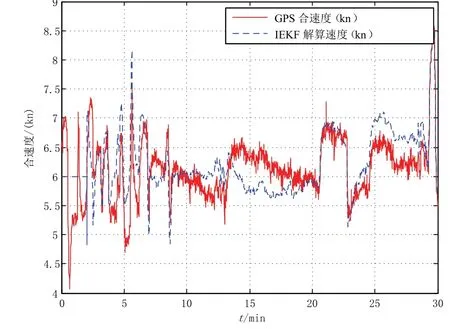
图2 IEKF 输出速度与GPS 速度Fig.2 Velocity of IEKF and GPS velocity
航向精度是初始对准方法是否可行的风向标,基于IEKF 的潜器动基座无源自对准的试验结果如表1所示。
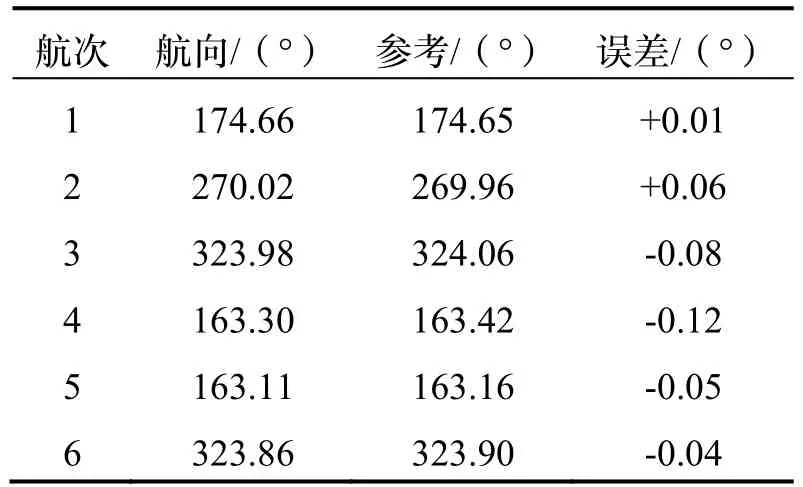
表1 对准结果及误差Tab.1 Alignment result and errors
从表1 的试验结果可以看出,基于IEKF 的无源动基座自对准方法的最大航向误差为0.12 °,最小为0.01 °,达到了惯性元件所对应的航向精度水平,方法的可行性与有效性得到了验证。
最后,将本文所设计的IEKF 滤波算法估计的航向角与传统EKF 滤波算法估计得到的航向角信息进行了试验对比。试验条件选取一个相对平缓没有红绿灯的路径,保证车速不会出现太大的突变,分别在朝向东和北的路面上进行跑车试验。发动车辆进入匀速运动状态后再进行设备通电,录取原始脉冲数,30 min后停车,同时记录此时参考基准设备的姿态角备用。两种方法仿真结果对比如图3所示。
由图3 可见,IEKF 能够快速收敛,在短时间内就收敛到小角度,而传统的EKF 刚开始方位失准角超调很大,并且最终没有达到收敛状态。这是因为传统EKF的系统矩阵依赖当前状态的估计值,当状态估计值与真值差距较大时,会直接导致依赖状态估计值的系统矩阵也有较大偏差,使用这样的系统矩阵继续传递误差,使误差又进一步放大,整个系统形成正反馈,最终导致滤波器发散。
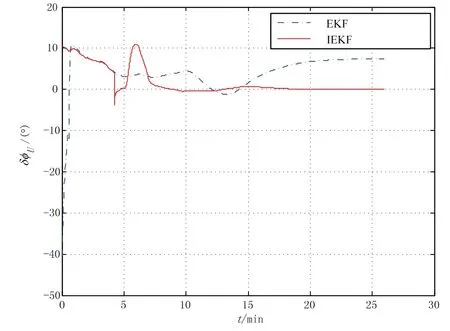
图3 EKF 和IEKF 算法的航向对准曲线Fig.3 Head curve using EKF and IEKF
4 结论
半实物仿真和跑车试验验证了所设计的IEKF 算法可以实现AUV 的无源动基座对准。试验结果表明:提出的方法在大失准角情况下依然能够保证较好的对准精度,使用陀螺偏差为0.01 °/h 的光纤陀螺,航向角在30 min 内收敛到1 mil 以内,达到了惯性元件所对应的航向精度水平,验证了该方法的有效性。与EKF方法相比,IEKF 算法不论是在精度还是在收敛性上,都优于EKF,但是在实现和计算负载方面与EKF 相似。在未来的工作中,我们希望不仅限于水下潜器的运动条件,也为其他载体的对准方法提供设计参考,以及研究是否可以将李代数与群变换应用于其他滤波算法,形成新的滤波器,如不变无迹卡尔曼滤波等。
