单轴旋转捷联惯导系统圆锥误差分析与仿真
2021-05-27程向红刘文倩
丁 鹏,程向红,刘文倩
(1.微惯性仪表与先进导航技术教育部重点实验室,南京210096;2.东南大学 仪器科学与工程学院,南京 210096)
在捷联式惯性导航系统(Strapdown Inertial Navigation Systems,SINS)中,陀螺仪直接固连于载体,敏感载体相对惯性空间的角运动。姿态算法的性能直接影响SINS 的导航精度,由于有限转动的不可交换性影响,姿态解算中不可避免地引入圆锥误差,尤其是在高动态环境下更为恶劣[1]。1971年Bortz 最早提出了等效旋转矢量概念,在理论上解决了不可交换性误差的补偿问题,后续众多学者在其基础上对圆锥误差补偿算法进行了研究[2-5]。
惯性测量单元(Inertial measurement unit,IMU)的测量精度是影响SINS 导航性能的主要因素,通过旋转调制技术在SINS 上加装一个转位机构,令IMU 按设计的方案进行旋转,通过旋转调制可有效抑制IMU的常值误差项,提高导航系统的精度[6]。虽然IMU 与载体之间不再直接固连,增加了转位机构和测角装置,但在导航解算上仍采用捷联惯导算法,因此也被称为旋转调制式捷联惯导系统(Rotational Strapdown Inertial Navigation Systems,RINS)[7]。20 世纪90年代,Sperry 公司研制出首台激光陀螺单轴旋转惯导系统,并成功应用于水面舰船和潜艇中[7]。后续国内外研究团队开展了基于激光陀螺和光纤陀螺的单轴、双轴和三轴旋转惯导系统的研制[8,9]。
在单轴RINS 中,IMU 安装在转位机构上并随之转动,相对纯SINS 其运动模型发生了改变,其不可交换性误差、圆锥误差补偿效果以及补偿后的剩余误差也将发生改变,目前尚未有针对单轴RINS 此方面的研究。针对上述转变,本文首先剖析了单轴RINS在典型圆锥环境下的运动形式,建立其运动模型并推导角速率拟合下的不可交换性误差,然后研究了基于角速率的旋转矢量算法和转位方案对圆锥误差补偿的影响,最后通过仿真实验验证理论分析的有效性。
1 单轴旋转捷联惯导圆锥运动特性分析
相对于SINS,单轴RINS 的圆锥运动模型和不可交换性误差均发生了改变,因此需要对其进行分析推导,为圆锥误差补偿算法在实际工程中应用提供参考。下面将以光纤陀螺惯导系统为例分析单轴RINS 的圆锥误差,所得的结论同样适用于输出信号为角增量的激光陀螺系统。
1.1 单轴旋转捷联系统圆锥运动描述
圆锥运动是惯性仪表感受到角振动的作用结果,当其两个正交轴上有同频不同相的正弦角振动输入时,第三个正交轴上便会输出常值角速度,称为等效陀螺漂移,它的产生会带来导航计算误差,即圆锥误差[1]。
本文所用的坐标系定义:导航坐标系n采用东-北-天地理坐标系;载体坐标系b按右-前-上构成右手直角坐标系;旋转坐标系r是三轴陀螺加速度计所指向的坐标系,因此在转位机构旋转起始时刻有。
在SINS 中,假设b系相对n系以为锥轴做典型圆锥运动,半锥角为α,圆锥运动角频率为则SINS 中t时刻的姿态四元数为:
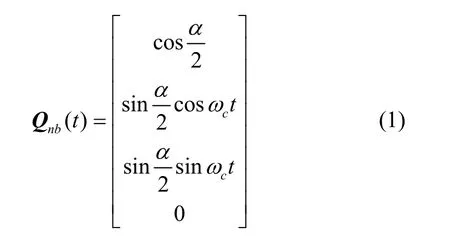
在单轴RINS 中IMU 安装在一个转位机构上,由于转位机构相对载体坐标系b存在转动,导致r系相对n系除了做典型圆锥运动外,还会随着转位机构绕转动,设其转速为则单轴RINS 中的圆锥运动可以表示为b系相对n系做圆锥运动与r系相对于b系做旋转运动的合成,则耦合转动下的圆锥变换四元数为:


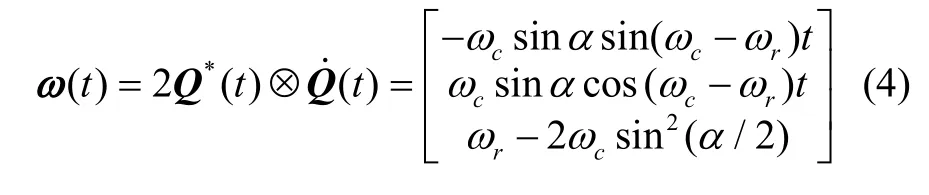
由式(2)和式(4)可得,当转位机构存在旋转角速度时,圆锥运动模型也将发生转变。
1.2 单轴旋转捷联惯导系统中圆锥运动的等效旋转矢量分析
由于刚体几何转动的不可交换性的影响,使得利用IMU 的输出在圆锥运动环境下进行导航解算时存在误差,体现在等效旋转矢量的计算误差。
以Q(tk)和Q(tk-1)分别表示在tk和tk-1时刻n系至r系的变换四元数,对应的姿态变化四元数为q(h),其中姿态更新周期h=tk-tk-1,根据四元数更新方程,有:

可得tk-1时刻至tk时刻对应于r系的四元数q(h):

根据姿态变化四元数q(h)与等效旋转矢量Φ(h)之间的对应关系,有:

式中,|Φ(h)|是矢量Φ(h)的模,由于姿态更新周期一般都很短,可认为Φ(h)为小量,简化式(7)得:

对比式(6)和式(8)的矢量部分可得:

2 单轴RINS 中转动不可交换性误差与圆锥误差补偿算法
在SINS 中,通常采用基于角速率/角增量的多子样旋转矢量算法补偿不可交换性误差。由于单轴RINS的圆锥运动特性发生改变,其补偿形式也将会不同,因此需要研究姿态算法和转位方案对圆锥误差补偿的影响。
2.1 转动不可交换性误差分析
虽然光纤陀螺的输出信号是角速率形式,但考虑到采样量化电路,故实际使用的光纤陀螺大都是在高速率采样的基础上再作平均和降频处理,其输出信息更像是角增量。文献[2]指出若将角速率形式信号转换成角增量进而构造等效旋转矢量,则在此转换过程中会引入较大噪声,为此设计了基于角速率输入的广义圆锥算法。基于角速率N子样圆锥补偿算法的基本原理是在每个姿态更新周期h内获得N+1 次陀螺采样角速率ωi(i=0,1,2,…,N),利用数值积分公式[2]由角速率估计角增量,并通过ωi之间的矢量叉乘对圆锥误差补偿项进行逼近,等效旋转矢量估计值ˆ()hΦ为:
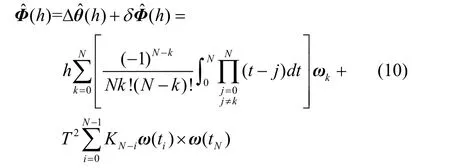
当(ωc-ωr)h和ωch都是小量时,即有sin[(ωc-ωr)h]=(ωc-ωr)h,sin[ωch]=ωch,角增量估计值为:
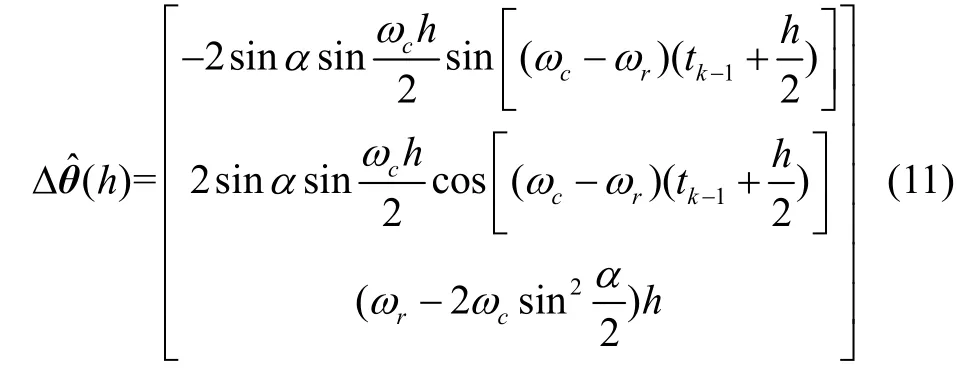
因此不可交换性误差的理论值近似为:

通过式(12)可以看出:
(1)基于角速率输入下的单轴RINS 的不可交换性误差在x轴与y轴分量为0,这与纯SINS 的圆锥误差一致。当(ωc-ωr)h和ωch不都是小量时,单轴RINS的不可交换性误差在x轴与y轴表现为周期量,其角频率为ωc-ωr,幅度与子样数有关。
(2)z轴常值误差分量中引入了ωr及其与α的耦合项,相对SINS 发生了变化。
2.2 基于角速率的圆锥误差补偿算法分析
在对不可交换性误差进行补偿时,将主要考虑其常量部分。根据式(12)有:
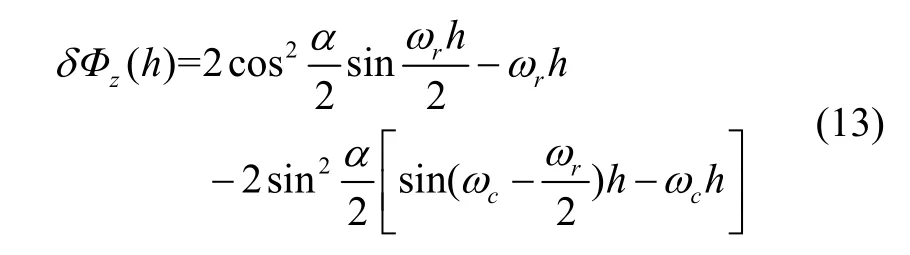
利用泰勒级数展开δΦz(h)中sin(ωc-ωr/2)h,可得:
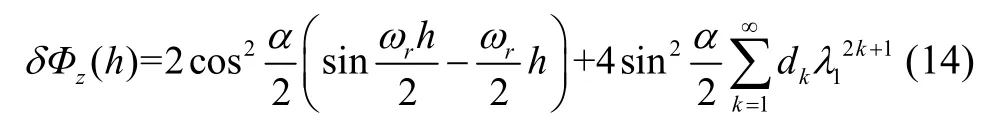
式中,dk=(-1)k+1N2k+1/[2(2k+1)!],λ1=(ωc-ωr/2)T。
文献[2]中基于角速率的圆锥误差补偿项通式为:
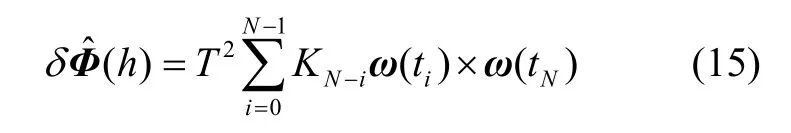
式中,KN-i为待优化系数,将角速率公式(4)代入到ω(ti)×ω(tj)且i≠j,得:
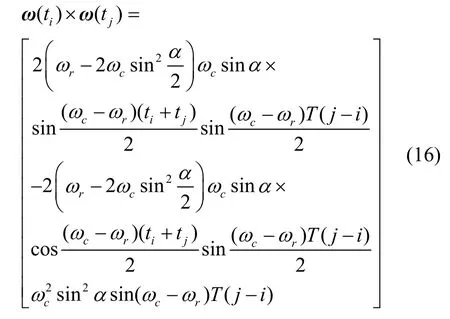

基于角速率的多子样旋转矢量算法常用式(17)对式(13)进行逼近,待优化系数为Kj(j=1,2…N),对于纯SINS,有λ1=λ2,因此可令式(17)和(13)相等,从而求解各子样下的Kj。但在单轴RINS 中,λ1≠λ2,Kj取决于ωc和ωr,而在实际系统中ωc无法获得,ωr也并非常值。根据实际工程中的应用,令单轴RINS 中的Kj与SINS 的圆锥优化系数一致,在此基础上对圆锥误差补偿后的剩余误差进行分析。
比较式(17)和式(14),可以看出在一个姿态更新周期内单轴RINS 圆锥误差补偿的剩余误差包括4 部分:
(3)λ1和λ2的差异在补偿时会产生误差。
(4)多子样算法在逼近圆锥补偿项时存在剩余误差,可近似为。
综合以上分析,可得单轴旋转捷联惯导系统N子样圆锥误差补偿算法的剩余误差为:

根据式(18),可将剩余误差分为3 类:
(1)εN的第一项误差与算法的子样数无关,由转位机构的旋转角频率所引起,不存在于SINS 中。
(2)εN的第二项误差与圆锥运动角频率、转位机构旋转角频率和算法子样数相关。在角频率不变下,增加算法的子样数可减小该项误差,SINS 中也存在类似误差。
(3)εN的第三项误差与圆锥运动角频率、转位机构旋转角频率和算法子样数相关,增加算法的子样数可减小该项误差,SINS 中不存在此类误差。
在SINS 中,圆锥误差的补偿精度随着子样数的增加而提高。但在单轴RINS 中,由于εN中第一项剩余常值误差的限制,使得多子样算法的补偿精度不再随子样数的增加而逐渐提高。
2.3 转位方案对圆锥误差补偿的影响
综合考虑转位方案对陀螺水平常值漂移的调制效果和实际工程应用成本,转位机构通常以多位置转停的方式进行正反方向旋转。而在实际系统中,转位机构的启停存在变速运动,即ωr是时间t的函数,若在转位方案中频繁引入变速运动,不仅会降低实际系统的误差调制效果,还会影响圆锥运动模型及其误差补偿效果。
(1)多子样算法补偿不可交换性误差后的剩余误差是通过时间累积来影响单轴RINS。当ωr在转动周期内表现为正反向对称时,εN中第1 项常值误差在每个转动周期内将相互抵消。
(2)在单轴RINS 的停留阶段,其圆锥运动模型及剩余误差εN与SINS 相同。
(3)转位机构的变速运动,不仅直接影响了IMU位置和速率的对称性,还间接影响了不可交换性误差的补偿效果。
3 仿真实验与分析
针对以上对单轴RINS 在圆锥运动下不可交换性误差补偿的理论推导与分析,将通过仿真比较转位方案对姿态误差的影响以及基于角速率的多子样旋转矢量法对圆锥误差补偿的效果。
3.1 单轴旋转捷联惯导系统中转位方案对圆锥误差影响仿真
仿真总体条件设置如下:半锥角α为1 °,圆锥运动频率为1 Hz,陀螺采样周期T=0.005 s,仿真时间20 min,假设b系相对n系做典型圆锥运动,姿态更新算法采用基于角速率的二子样旋转矢量算法。
当旋转角速度ωr为0 时,其姿态误差如图1所示;当转位机构以ωr=16 °/s 单方向持续旋转时,其姿态误差如图2所示;当转位机构以旋转角速度ωr=16 °/s,旋转角加速度ar=8 °/s2单位置正反转停时,其姿态误差如图3所示,停转时间为2.5 min;当转位机构以ωr=16 °/s,ar=8 °/s2四位置转停,四位置转位停的顺序为:0 °→180 °→270 °→90 °→0 °,其姿态误差如图4所示。其中ΔH、ΔP、ΔR分别表示载体的航向角、俯仰角和横滚角误差。
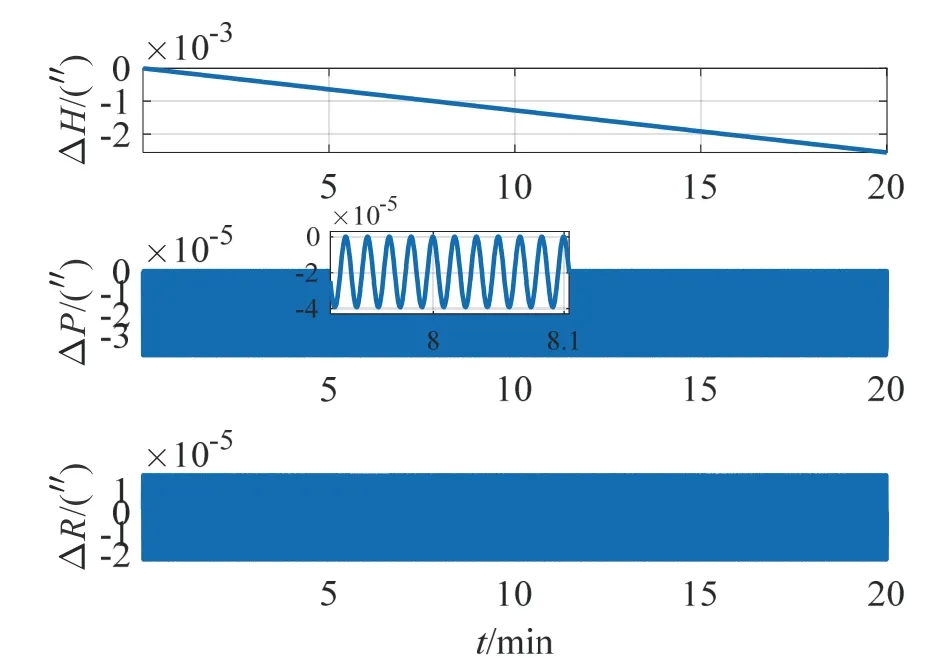
图1 零速旋转下姿态误差Fig.1 Attitude error under zero speed rotation

图2 单向匀速旋转下姿态误差Fig.2 Attitude error under unidirectional rotation
由图1 可以看出,转位机构停转条件下的姿态误差变化与SINS 一致;相对零速转动,图2 中当转位机构存在转速时,航向角误差增大0.6 倍,水平姿态角误差波动幅度增大1~2 个数量级。对比图2、图3和图4 可知,通过转位机构的正反转可降低航向角误差和水平姿态角误差,但由于在启停过程中引入了变速运动,导致水平姿态角误差在短时间内有剧烈的周期振动,比停转阶段的误差幅度大2~3 个数量级。单轴RINS 在圆锥运动下的水平姿态角误差仍是呈现出周期性变化,故主要考虑航向角误差,四种转位方案下的航向角误差仍随时间发散,由表1 知四位置转停方案下的航向角误差最小,但其启停阶段的航向角误差要比停转阶段的误差大3 个数量级,持续时间取决于启停的时间差,在本节仿真中转过90 °和180 °所需的时间分别为7.625 s 和13.25 s。

图3 正反转停下姿态误差Fig.3 Attitude error under reversible switch-stop

表1 仿真20 min 后航向角误差Tab.1 Heading error after 20 minutes of simulation

图4 四位置转停下姿态误差Fig.4 Attitude error under four-position switch-stop
3.2 四位置转停下基于角速率的多子样旋转矢量算法对圆锥误差影响仿真
仿真总体条件设置如下:半锥角α为1 °,圆锥运动频率为1 Hz,旋转角速度ωr=16 °/s,旋转角加速度ar=8 °/s2,陀螺采样周期T=0.005 s,仿真时间20 min,假设b系相对n系做典型圆锥运动。四位置转停的顺序为:0 °→180 °→270 °→90 °→0 °,转位机构的旋转角度和角速度如图5所示,包括匀加速、匀速、匀减速和停转四个阶段,停转时间为2.5 min。分别采用基于角速度的三子样、四子样和五子样等效旋转矢量算法对单轴旋转捷联惯导的圆锥误差进行补偿后,其姿态误差分别如图6、图7 和图8所示。

图5 转位机构的角度和角速度变化Fig.5 Change of angle and angular velocity of indexing mechanism

图6 三子样算法姿态误差Fig.6 Attitude error of triple-sample algorithm

图7 四子样算法姿态误差Fig.7 Attitude error of four-sample algorithm
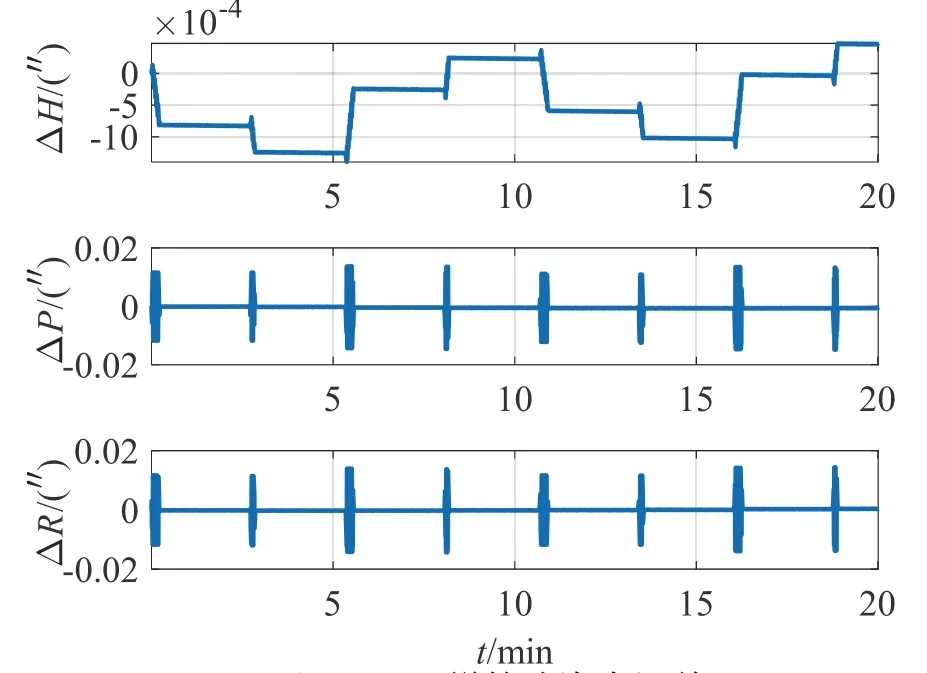
图8 五子样算法姿态误差Fig.8 Attitude error of five-sample algorithm
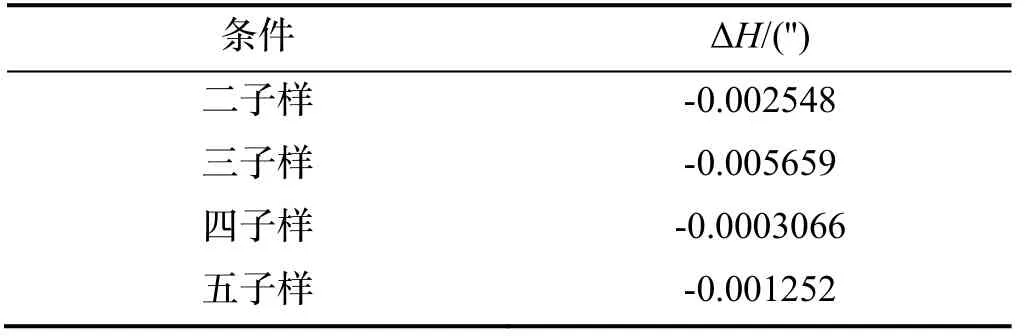
表2 停转阶段最大航向角误差Tab.2 Maximum heading error during stop phase
对比图4、图6、图7 和图8,可以看出,在陀螺采样频率固定的情况下,由于不同子样算法的姿态更新周期不同,导致圆锥误差补偿效果未因子样数的增加而提高。其中三子样补偿后的水平姿态误差最大且呈发散趋势,五子样补偿后的航向角误差呈阶梯式变化。由表2 知,采用四子样补偿算法下的航向角误差最小,且水平姿态角误差呈现周期变化,补偿效果相对较好。结合工程实际中IMU 输出频率固定和计算实时性要求,可采用基于角速率的四子样补偿算法。
4 总结与展望
本文通过理论分析和仿真,得出以下结论:
(1)单轴RINS 的圆锥误差及其补偿后的剩余误差大于SINS 中的误差,通过增加基于角速率/角增量的旋转矢量算法的子样数不能无限提高圆锥误差补偿精度;转位方案会影响圆锥误差的补偿精度,四位置转停方式的误差补偿效果最好。
(2)在四位置转停方案中,启停阶段的航向角误差会急剧增大,其持续时间在10 s 左右,虽然对RINS的导航定位解算影响不大,但对以RINS 为主的组合导航系统来说可能会造成滤波校正后的结果变差,故应尽量降低RINS 启停频率或延长停转时间。
(3)RINS 中圆锥误差随载体摇摆幅度和摇摆频率的增大而增大;现有圆锥算法大都在假设陀螺输出无误差的前提下设计姿态误差补偿系数且其实际精度尚未得到验证,然而陀螺输出信号中包含了随机误差、安装误差、标度因素误差和量化等误差,导致实际信号中难以保留理论运动假设下的全部特性,进而造成圆锥误差补偿效果不理想,因此如何提高高动态条件下圆锥误差的实际补偿精度是下一步的研究方向。
