基于社会等级淘汰机制的GWO_PSO算法
2021-05-27张子豪靳其兵
张子豪,靳其兵
(北京化工大学 信息科学与技术学院,北京 100029)
群智能优化算法是一种由自然界中,群体动物的活动启发而产生的全局优化算法。典型的智能优化算法包括粒子群优化(Particle swarm optimization,PSO)[1]算法,差分进化(Differential evolution,DE)[2]算法,鲸鱼优化算法(Whale optimization algorithm,WOA)[3],人工蜂群(Artificial bee colony,ABC)[4]算法,布谷鸟(Cuckoo search,CS)[5]算法等。智能优化算法在机器学习算法[6-8]、系统辨识[9,10]以及PID控制方面[11]也有很多的应用。
Mirjalili等[12]由灰狼猎食以及灰狼种群中的等级制度得到启发,于2014年提出灰狼优化(Grey wolf optimizer,GWO)算法,其结构简单,参数少,易于编程,寻优性能较好,但其自身仍然存在收敛精度不足的问题。近年来,对此有很多学者提出了对灰狼算法的改进方法,文献[13]通过加入混沌策略和对收敛因子加入自适应策略,使算法精度和稳定性都有了一定的提高;文献[14]通过改进收敛因子的方法,使其不易陷入局部最优;文献[15]引入PSO的最优解记忆思想,采用佳点集策略和改进收敛因子的策略,提升了算法的性能;文献[16]引入差分进化算法的和灰狼算法混合的策略和优胜劣汰法则,改进了灰狼算法的寻优能力。
1 GWO算法原理
灰狼算法是受到灰狼狩猎觅食这一自然现象启发,而提出的群智能优化算法,灰狼优化算法在设计中考虑了狼群中的社会等级,模仿狼群寻找、包围、攻击猎物的狩猎模式。
(1)社会等级(Social hierarchy)。
该算法设计了3种统治阶级的狼和普通的狼,统治阶级的狼分为α狼、β狼、δ狼,组成狼群的普通狼为ω狼,其分别对应的是最优解、次优解、第三优解和候选解[17]。
(2)围猎(Encircling prey)。
灰狼在搜索猎物的过程中,会逐渐地接近猎物并包围它,该行为的数学模型如下
D=|C·Xp(t)-X(t)|,X(t+1)=Xp(t)-A·D
(1)
式中:t指当前时刻,A和C是协同系数,Xp是头狼的位置,X是指灰狼ω狼群的位置。
协同系数A、C分别为
A=2a·r1-a,C=2·r2,a=2-2*(t/tmax)
(2)
式中:a由2线性衰减到0,r1和r2是[0,1]之间的随机数。
(3)狩猎(Hunting)。
在每次迭代过程中,保留当前种群中的最优的3只灰狼,即适应度值最优的3个解,α狼、β狼、δ狼,头狼根据他们自身所在位置,判断狼群与自己的距离,并通过商议,得出狼群所需移动的距离。该行为的数学模型可表示为
Dα=|C1·Xα-X|,Dβ=|C2·Xβ-X|,
Dδ=|C3·Xδ-X|
(3)
X1=Xα-A1·(Dα),X2=Xβ-A2·(Dβ),
X3=Xδ-A3·(Dδ)
(4)
X(t+1)=(X1+X2+X3)/3
(5)
式中:Dα、Dβ、Dδ分别表示3种头狼与猎物之间的距离,X1、X2、X3分别表示α狼、β狼、δ狼的位置,式(5)表示ω狼根据α狼、β狼、δ狼的位置更新整个狼群的位置。
2 PSO算法原理
PSO算法是Kennedy和Eberhart提出的一种群智能优化算法。粒子群优化算法的基本思想是利用种群中不同粒子之间的信息共享,使群体由随机分布到有序分布,其速度向量的思想,对于群智能优化算法来讲是有开创意义的。
粒子群优化算法将每一个粒子随机分布在解域空间内,设粒子的位置为X,根据适应度值设置局部最优Xpbest和全局最优Xgbest,Xpbest表示当前代适应度值最优的粒子,Xgbest表示历史代到目前最优的粒子。根据局部最优和全局最优可以得到一个速度矢量V,其公式为
V(t+1)=ωV(t)+c1r1(Xpbest(t)-X(t))+
c2r2(Xgbest(t)-X(t))
(6)
式中:c1=2,c2=2,ω表示惯性因子,通常由大到小线性收敛,值大时主要进行全局搜索,值小时进行局部搜索。其更新公式为
ω(t)=ωmax-(ωmax-ωmin)*t/tmax
(7)
式中:tmax表示迭代的最大代数,通常ωmax=0.9,ωmin=0.4。
根据得到的速度向量V更新粒子群中的每一个粒子,其表达式为
X(t+1)=X(t)+V(t+1)
(8)
3 灰狼_粒子群智能优化算法
针对灰狼算法中仍然存在寻优精度低,收敛速度慢的问题,本文提出了一种灰狼_粒子群智能优化(Grey wolf optimizer_particle swarm optimization,GWO_PSO)算法。
3.1 GWO_PSO算法改进思路
(1)混沌映射。
混沌映射具有随机性、周期性的特点。在许多智能优化算法中,混沌映射都起到了很好的效果,如文献[18]采用了Iterative映射的方法初始化狼群。
Logistic映射通过迭代的方式产生,是一种具有确定性、类似随机性、非周期的、收敛性的伪随机序列,其分布均匀。为使灰狼狼群更随机地分布,引入Logistic映射对灰狼狼群进行初始化。Logistic映射的公式为
uk+1=auk(1-uk)
(9)
从图1中可以看出,当a=4时,Logistic在[0,1]分布最广,其中uk∉{0,0.25,0.5,0.75,1}。如图2所示,Logistic映射的分布更加随机,因此选用Logistic映射用于初始化灰狼种群。
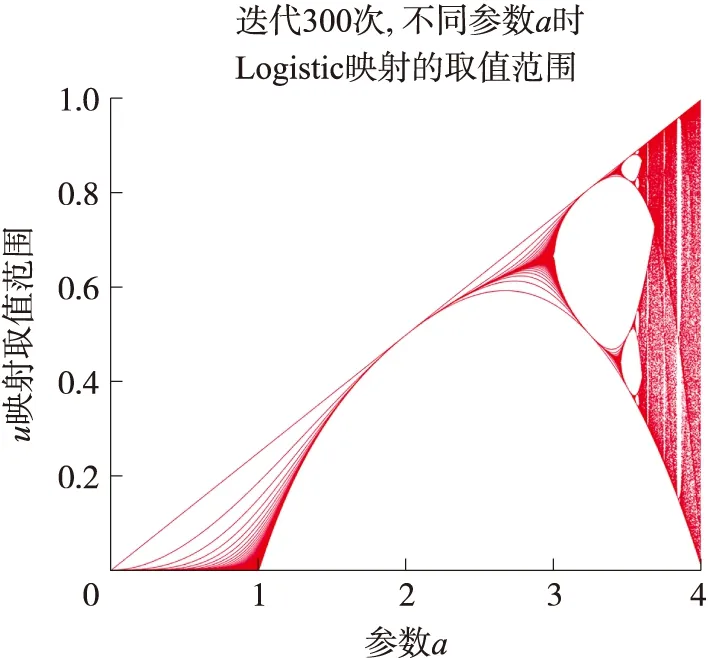
图1 参数a对应的Logistic映射
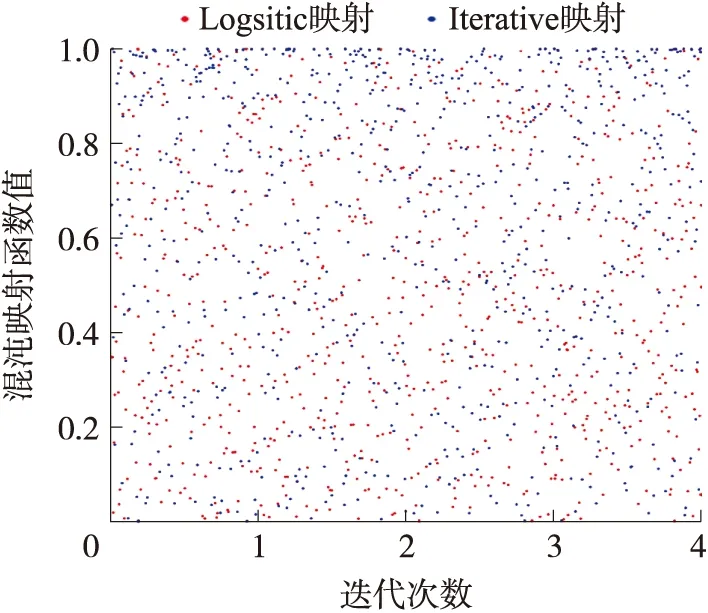
图2 两种混沌映射的分布
(2)等级制度。
灰狼算法中提出的等级制度没有体现出3只头狼的优先级的差别,容易偏离目标值,导致精度不足。为了凸显灰狼算法的等级制度,提出灰狼算法的等级制度思想,其基本思想就是在更新灰狼位置时,加上一个等级权重,分别为η1、η2、η3,三者的关系为
η1∶η2∶η3=4∶3∶2
(10)
通常取η1=2、η2=1.5、η3=1。
(3)速度向量。
灰狼算法中的位置更新只体现了灰狼和猎物之间的距离,并没有体现出灰狼寻优的方向,其对于解的判定只有位置信息而没有方向矢量信息,其优化能力还有一定地提升空间。受粒子群优化算法中速度向量V的启发,根据式(3)、(4)、(5)计算得到头狼及狼群的位置,引入速度向量V,其更新公式为
(11)
式中:ω为惯性因子,ηi为等级权重,k为协同系数。
通常ωmax=0.6,ωmin=0,ω的选择对于寻优效果有着重要影响,其更新公式为式(7)。
协同系数k的公式为
k=0.1*rand
(12)
灰狼狼群的位置更新公式为式(8)。
通过引入速度向量,增加了寻优方向矢量信息,提高了收敛速度和收敛精度。
(4)淘汰机制。
一个灰狼种群中,存在一些老弱病残的灰狼,随着自然选择,会被新生的狼群代替,同时统治阶级的狼有更多的繁衍机会。在每一代ω狼中,选取适应度值在排在后三分之一的灰狼予以淘汰,同时由新一代的灰狼替代被淘汰的老弱病残,其更新公式为
(13)
式中:η1、η2、η3为等级权重。
淘汰机制的主要流程为:
(1)根据适应度值排序ω狼,并对适应度值排后三分之一的灰狼Xold予以淘汰。
(2)根据式(13)得到Xnew,替换Xold,与之前的灰狼形成新的种群。
淘汰机制强化了等级制度在灰狼算法中的作用,使算法的精度和收敛速度有所提高。
3.2 GWO_PSO算法流程
通过以上改进,提高了灰狼算法的精度和收敛速度,经过总结,可以将其归纳成如下步骤:
步骤1初始化。采用Logistic混沌映射,初始化灰狼种群X,并初始化参数;
步骤2计算适应度值。计算灰狼狼群X的适应度值,根据适应度值设α狼、β狼、δ狼,其包含的猎物信息分别是Xα、Xβ、Xδ,通过式(3)和式(4)得到X1、X2、X3;
步骤3根据式(5)获取ω狼群的猎物信息;
步骤4根据式(11)计算速度向量V,并将其代入式(8)更新种群位置;
步骤5淘汰机制。根据步骤2所计算的适应度值,进行排序,淘汰后三分之一的灰狼Xold,并根据式(13)得到Xnew;
步骤6计算灰狼适应度值,和上一代迭代的值比较,根据适应度值选择新的α狼、β狼、δ狼,得到X1、X2、X3;
步骤7判断Xα的适应度值是否达到结束条件,若满足条件,则最优值为Xα;若不满足条件,则重复步骤4-7。GWO_PSO优化算法流程如图3所示。

图3 GWO_PSO算法流程图
4 函数优化实验及结果分析
为测试GWO_PSO算法的有效性,本文采用12个经典的测试函数,其表达式如表1所示。

表1 12个测试函数表

续表1
为了体现本文所提算法对灰狼优化算法的改进效果,本节将对GWO_PSO算法与其他改进灰狼算法进行比较,分别选取F1~F12函数比较,测试函数F9为2维,其余函数为30维。将GWO_PSO与LGWO[19]、HGWO[20]、PGWO[21]、CGWO[22]比较,运算500次得到的平均值及标准差,其结果如表2所示。部分函数适应度收敛曲线如图4-6所示。
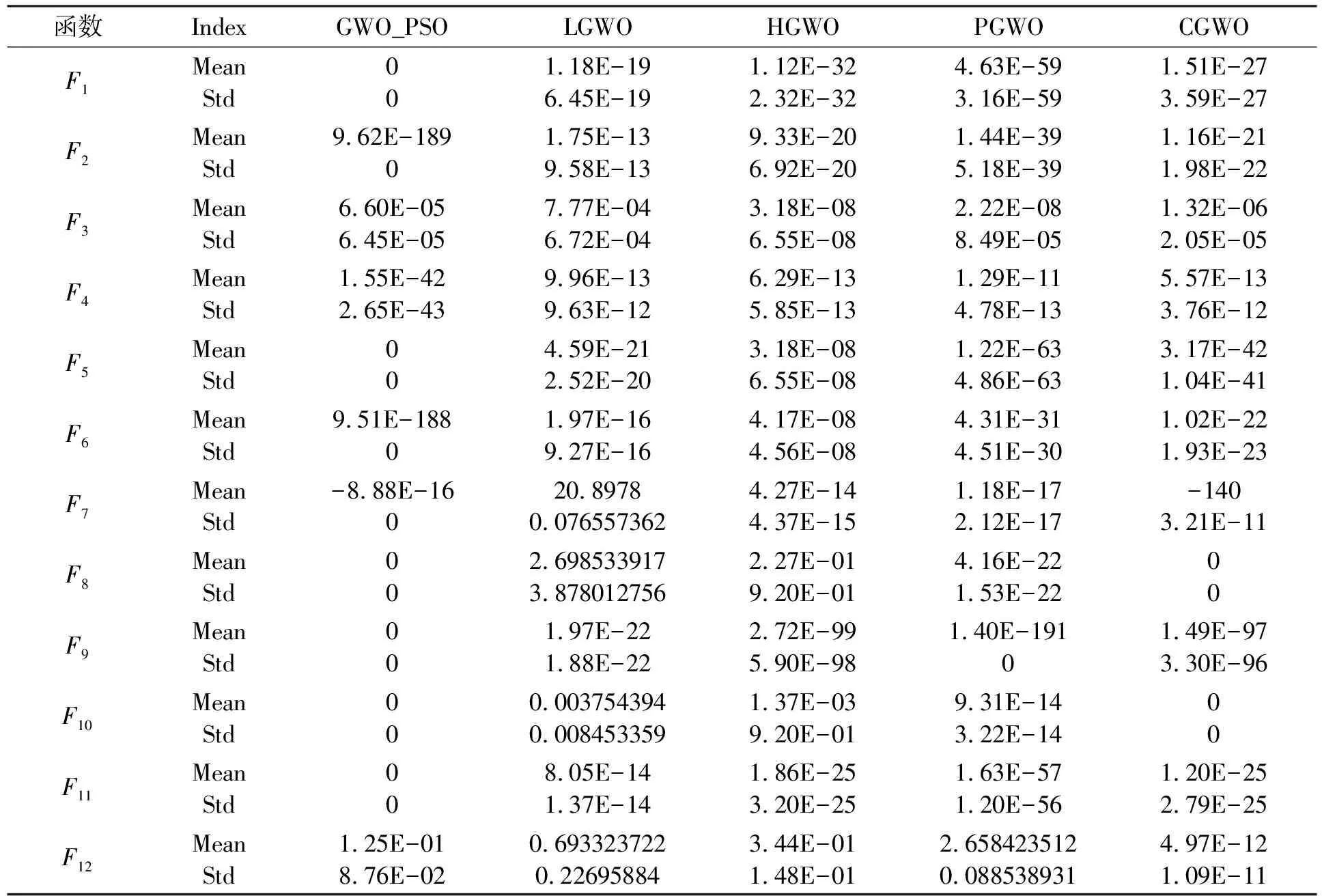
表2 GWO_PSO与4种灰狼算法的寻优效果比较

图4 F1函数收敛曲线

图5 F2函数收敛曲线
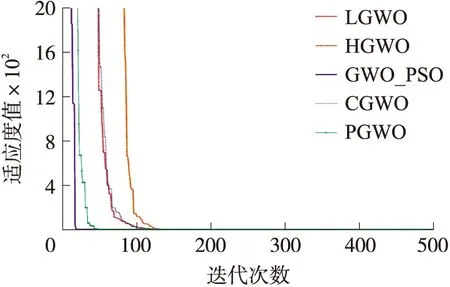
图6 F6函数收敛曲线
5 结论
本文提出了一种基于淘汰机制的GWO_PSO算法,引入了Logistic混沌映射策略初始化种群,使初始种群分布更加均匀;提出等级制度,突出了GWO算法中狼群的等级机制;引入速度向量思想,提高收敛精度及速度;提出了狼群中的淘汰机制,剔除了狼群中的“害群之马”。同时根据狼群社会中的等级制度,让狼群中等级更高的狼拥有繁衍权,提高了算法的精确度,提高了算法的收敛速度。在系统辨识问题中,该算法取得了很好的应用效果。
