奇异品质大米的外观特征分布研究

杨志晓 范艳峰 杨 柳

(河南牧业经济学院能源与智能工程学院1, 郑州 450011)(粮食信息处理与控制教育部重点实验室；河南工业大学2, 郑州 450001)

储粮品质随储藏时间和环境的改变会发生变化。近年来，采用计算机视觉、模式识别、机器学习等技术，从颜色、几何、纹理等特征进行自动品质检测，已成为非常有前景的粮食品质检测手段[1-3]。研究储粮外观特征变化规律，有助于实现储粮品质的快速检测。

粮食品质检测的研究主要聚焦于图像分割、特征提取、分类方法等方面。图像分割的目的是把粮粒图像从背景中提取出来，如对水稻品种采用阈值法边缘检测[4]和粒化阈值分类方法[5]，综合分水岭算法、形态测地活动轮廓和无边缘形态活跃轮廓的分割算法[6]，综合使用HSI(色调、饱和度和强度)背景颜色模型和形态学算子、分水岭变换以及基于投影面积和圆度的组件标记方法[7]，综合均值漂移滤波器、颜色梯度、标记分水岭变换的分割方法[8]，基于数学形态学和相关性粒度测量方法[9]等。

提取的粮粒特征包括图像区域、长轴长度、短轴长度、长宽比、周长、偏心率、色调、饱和度、强度、破损、裂纹、霉变、虫害等[5-10]。

采用的分类方法有AdaBoost，支持向量机[10]，主成分分析结合BP神经网络[11]，综合图像小波矩特征、最小欧式距离判别器和随机森林的方法[12]，主成分分析和层次聚类方法[13]，傅里叶变换与偏最小二乘回归法[14]，基于组合特征的稀疏表示和字典学习技术[15]，深度信念网络[16]等。

粮食是典型的散粒体，粮食品质由大量粮粒的品质综合体现。而粮食品质在每个粮粒的表现却具有随机不确定性。品质间的特征值域并不存在清晰的边界。由此带来的问题是，虽然可以根据已知品质粮食样本训练分类器，但在使用训练过的分类器预测新样本时，无法断言新样本的类别归属。这是由于在特征值交叠区，某一特征值的样本可能属于一个类别，也可能属于其他类别。而当前主流的机器学习方法将给定样本唯一地归属于某个类别，因而不能处理粮食品质的不确定性问题。尤其在检测将不同品质(如新与陈、优与劣、贵与贱、不同品种)混合的奇异粮食样本时，现有分类方法无法准确判断被试样本整体的品质、奇异性及奇异时的混合比。

从特征分布的角度考察粮食等散粒体，是一种较为有效的解决方法。特征分布反映大量粮粒样本品质的整体特性，具有可靠、稳定的优点。将不同品质粮食混合的奇异样本，其特征分布将发生改变。根据特征分布的变化情况，可推断出被试的品质、奇异性、混合比。以大米的颜色特征为例，研究大米颜色的分布随储藏时间的变化规律，提出一种基于特征分布的储粮品质检测及奇异性判断方法。

1 材料与方法

1.1 主要材料

大米，常温露天储藏。以7周为时间周期，获得相对储藏期分别为0、7、14周的大米样本，作为3个不同的大米品质类别。

1.2 大米颜色样本采集

对每个品质大米样本，随机选择195粒大米，分散放置于黑色背景平面上，拍摄图像。为便于观察，截取部分图像如图1a所示。

使用Python编程语言和scikit image图像处理库，将大米的原始图像变换为灰度图像，将灰度图像二值化。对二值化图像进行膨胀、腐蚀、闭合运算，将米粒图像与背景分割，获得米粒图像区域像素位置索引、质心、长短轴方位及它们的长度。

根据获得的上述信息，在原始图像上对米粒图像用矩形框将其标记，以便于观察是否有遗漏米粒或标记错误的区域。并绘制米粒图像区域的长、短轴半轴，如图1b所示。对每个米粒图像，选择质心、长短轴上共21个点，提取其RGB颜色和灰度特征，采样点如图1c所示。

图1 大米粒的原始图像、分割标记和颜色采样点

如此对每个品质的大米样本，分别获得15 795组RGB(红、绿、蓝)和灰度的颜色样本。为消除光照变化的影响，将每幅图像的大米颜色值按照极差标准化转换到[0,1]区间。

将建立的三个储藏期的大米颜色样本，视为3个品质类别，分别以标签0, 1, 2进行标记。如此得到行、列形状为(47 385, 4)的大米颜色特征值集和47 385个类标签的目标集。

1.3 数据处理

1.3.1 非奇异样本的目标概率分布估计

建立的3个大米品质类别，每个类别的所有米粒属于同一类别，即每个类别样本是纯的、非奇异的。对它们的大米颜色数据集，分别估计其颜色值概率分布，作为3个类别的相应的目标概率分布。

非奇异目标概率分布的估计方法是，将[0,1]区间进行N等分，分别对每个品质的大米颜色样本，统计计算各通道颜色值落在每个区间的频率，作为该颜色值的概率密度估计。它们即是非奇异样本的目标概率分布。

1.3.2 奇异样本的目标概率分布估计

所谓奇异样本，本文指将不同品质大米混合在一起的混合样本，如新与陈、优与劣、贵与贱、不同品种大米的混合等。为简化问题，暂考虑只有二元类别混合的情况。将两种类别的大米样本分别按照9∶1, 7∶3, 5∶5, 3∶7, 1∶9进行二元混合，且混合后的颜色样本数量与纯的样本数量相同。按照同样的方法，估计各个混合比下的样本颜色值分布，作为相应混合类别和混合比的目标概率分布。

2 结果分析

2.1 储藏大米的颜色值分布变化规律

图2展示了将[0,1]区间等分为30个区间，储藏期分别为0、7、14周的R, G, B,灰度的概率估计的分布。

可以看出，不同储藏期的大米颜色值概率分布呈现显著差别，主要表现为峰值右移，其中红色的峰值右移现象最为明显，说明不同储藏期的大米品质存在差异。图2即为3个纯(非奇异)类别c0, c1, c2的各颜色值的目标概率分布。

2.2 大米红色值非奇异样本的目标概率分布

从图2可以看出，三个品质的大米红色值的概率分布差别最大。选择红色作为主要特征。将标准化后的红色值区间[0,1]等分为30份，统计各个类全部样本落入每个区间的频率，得到的3个类别红色值概率估计的分布如图3所示。它们即是3个纯类别c0, c1, c2的红色值的目标概率分布。

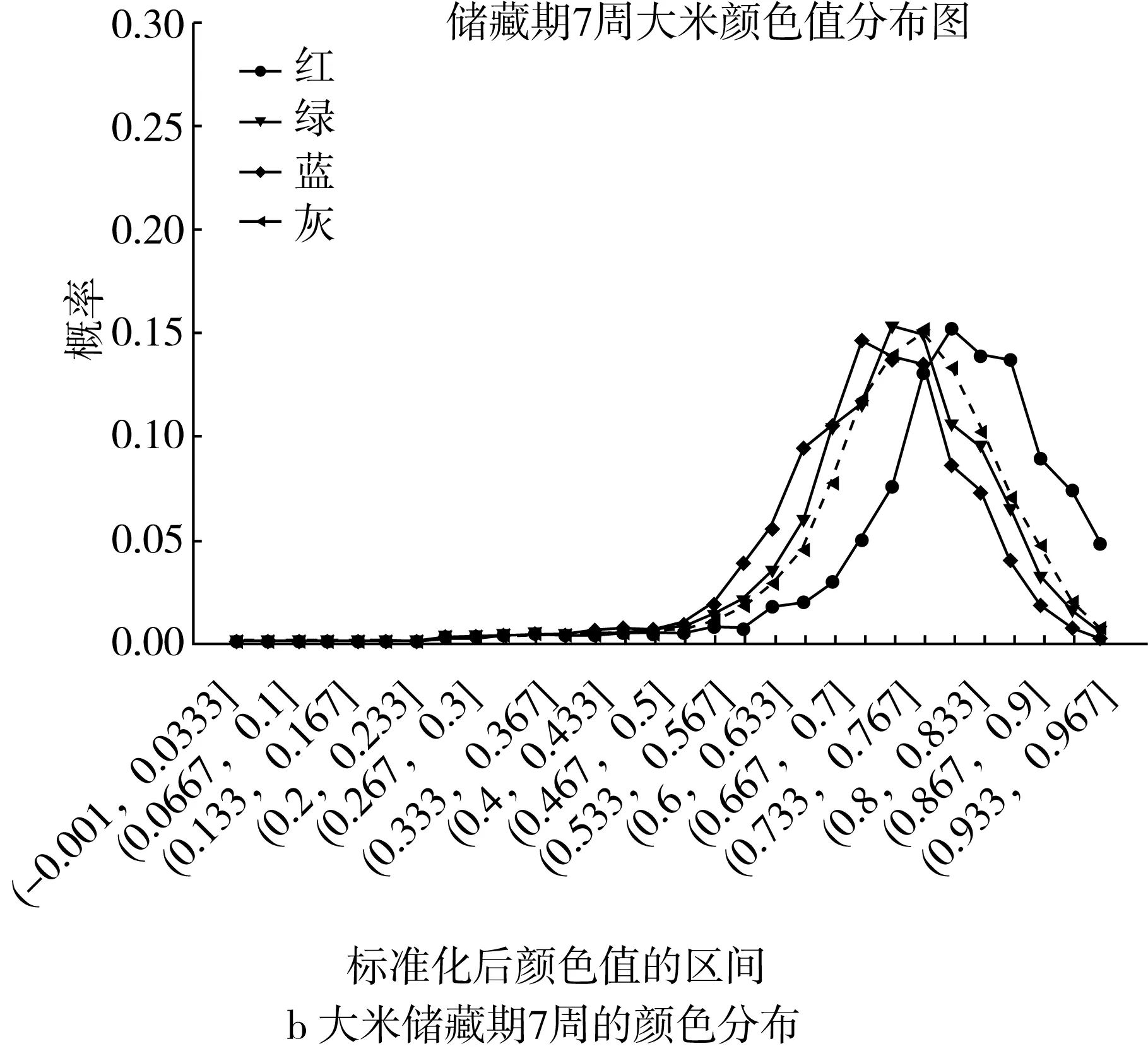
图2 不同储藏期大米颜色值的分布

图3 三个大米品质类别的红色值分布

图4 类c0和c2在不同混合比的红色值概率分布

2.3 大米红色值奇异样本的目标概率分布

奇异样本即为将不同品质大米混合在一起的样本，暂只考虑二元混合的情况。这里选择类0和2，分别按照9∶1, 7∶3, 5∶5, 3∶7, 1∶9进行二元混合，每次混合保持样本总数量为15 795，即为单个纯类别的样本数量。另外，将无混合的类0和类2分别视为它们以10∶0, 0∶10的比例混合。

对混合样本，将标准化后的红色值区间[0,1]等分为30份，统计各个混合比下样本落入每个区间的频率，作为样本的概率密度估计。得到的7种混合比样本红色值概率分布如图4所示。由于前10个区间的概率非常小，限于篇幅，表1给出了7种混合比样本的红色值在后20个区间的概率值。

将图4中c0和c2大米红色值不同混合比的概率分布，作为c0和c2的二元混合目标分布。它们将作为样本奇异性判别的参考标准。将这些概率分布作为基本分类样本，每个概率分布对应的样本类别混合比作为类标签，建立基于特征分布的分类样本数据集。

2.4 基于分布的大米品质奇异性判别

2.4.1 基于分布的大米品质奇异性判别方法

要判断被试样本的品质是否奇异，首先估计它的特征分布，与已建立的目标特征分布对比，将其划分为与目标特征分布最接近的样本所对应的类别。由此判定被试样本是否奇异(有无混合)，以及奇异样本的混合比。

表1 大米红色值在不同混合比的目标分布

若将特征X的值域区间等分为N份，则它在N个区间的概率分布可以表示为PX=[p1,p2,…,pN]. 记特征X的某个目标分布为PX0=[p10,p20,…,pN0]. 被试样本的特征X的分布为PX=[p1,p2,…,pN]. 构造均方误差函数如式(1)所示。

(1)

对特征X的所有目标分布{PX0(k)|k=1,2,…,K}，分别按照式(1)计算被试特征分布与它们的均方误差，可得到一组均方误差值{MSEX(k)|k=1,2,…,K}. 找到均方误差的最小值，将被试划分为取得最小均方误差的目标分布所对应的样本类别。

本文中，大米红色的目标特征分布有7个，即c0与c2按10∶0, 9∶1, 7∶3, 5∶5, 3∶7, 1∶9, 0∶10的比例进行混合所得到的概率分布，对应1个纯c0类别、5个奇异样本类别和1个纯c2类别。

基于特征分布的样本奇异性判定和分类方法可以描述为：

a)输入特征X的值域及等分区间数量N；

b)输入特征X的所有目标分布{PX0(k)|k=1,2,…,K}；

c)估计被试样本特征X的分布PX=[p1,p2,…,pN]。

d)按照式(1)计算PX与所有目标分布的均方误差{MSEX(k)|k=1,2,…,K}；

e)将被试划分为min{MSEX(k)|k=1,2,…,K}所对应的类别。

由于特征目标分布的类标签为大米品质类别及其混合比，则根据本算法的分类结果可以知道被试是否奇异(纯或混合)、奇异样本的混合物类别和混合比。

2.4.2 算法性能分析

为验证基于特征分布的散粒体奇异性判定和分类方法，按给定混合比，随机从c0和c2中选择共10 000个红色值，建立奇异样本，估计它的概率分布，分别计算它与各目标概率分布的均方误差，将其划分为使均方误差取得最小值的特征目标分布对应的样本类别。

重复操作1 000次，记录每次分类结果，统计分类正确的次数、分类错误的次数、以及错误划分到的类别及次数。

改变被试样本的混合比，重复上述实验过程。

改变红色值域等分区间数量N，重复上述实验过程。

实验结果表明，特征X的值域区间等分数量N较小时，分类结果存在误差。当N≥25时，分类算法对被试样本的分类准确率、召回率均为100%。本文取N=30。

一个c0和c2按5∶5混合的被试样本概率分布与所有目标概率分布的对比如图5所示。可以看出被试与5∶5混合的目标概率分布几乎重合，而与其他目标分布则存在明显差别。

图5 被试红色值概率分布与目标分布对比

图6给出了将c0与c2分别按10∶0, 9∶1, 7∶3, 5∶5, 3∶7, 1∶9, 0∶10的比例进行混合得到的各一个被试样本红色值概率分布与目标分布的对比，可以看出每个被试样本的红色值概率分布几乎与对应的目标分布重合。

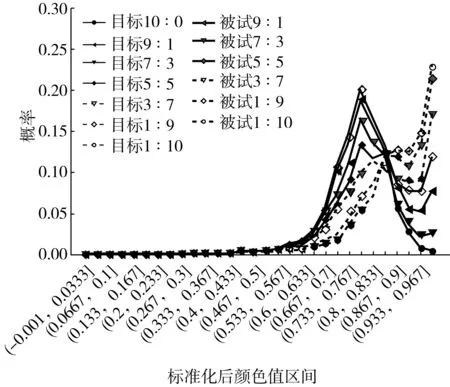
图6 不同混合比被试红色值概率分布与目标分布对比

从实验结果可以看出，所提出的基于特征分布的分类方法能够很好地判断被试样本是否奇异，并且在认为样本奇异时，能够量化其混合比。

基于特征分布的分类算法的计算开销主要在图像处理与特征提取、样本的概率密度估计和被试与目标特征分布间的误差计算，并不需要反复迭代，与常用的分类方法相比，其算力开销几乎可以忽略不计，因此具有优异的性能。

2.5 讨论

以大米为典型代表的散粒体特征分布由众多个体的统计特征综合体现，具有稳定性。少量个体的变化不影响整体特征分布。如果被试的特征分布发生了变化，则一定有相当数量的个体特征发生了变化，由此可以判定被试奇异。

只要不同“纯”类别的特征分布不同，它们二元混合后的特征分布就会发生改变，将被试的特征分布与已建立的目标分布对比，可以判断被试是否奇异，以及在奇异时推断其混合比。

大米的品质类别是可以穷举的，因此可以建立任何品质类别及两两间给定混合比下的目标特征分布，作为检测被试奇异性及奇异时推断混合比的依据。

被试可能存在实际混合比与已建立的目标分布所对应的混合比都不一致的情况。此时算法的运行结果将其划分到使均方误差取得最小值的目标分布所代表的类别。则实际混合比与识别结果存在误差。如果从实用的角度该误差不能接受(例如将实际6∶4的混合比推断为5∶5仍造成较大的经济损失)，可以通过考察更多二元混合比(如8∶2, 6∶4, 4∶6, 2∶8)的情况，以丰富不同混合比下的目标分布，将误差降低到可以接受的范围内。

本实验对大米主要考察其颜色尤其是红色特征。这主要是由于不同品质类别间红色特征分布差别最大。实际上，对其他颜色特征，以及纹理、几何形状等特征，都可以建立它们相应的目标特征分布，作为检测被试奇异性的依据。

3 结论

针对粮食可能存在的诸如新陈、优劣、贵贱等不同品质混合的奇异性问题，以大米为对象，分析了颜色分布随储藏时间的变化规律，研究了一种基于特征分布的散粒体奇异性识别方法，主要结论如下：

常温露天储藏大米在相对储藏期0、7、14周的颜色分布具有显著差异，主要表现为各颜色概率分布峰值右移，红色值概率峰值右移现象最为明显。

建立了3个相对储藏期大米颜色的各自的目标概率分布，建立了储藏期为0周、14周两类样本分别按9∶1, 7∶3, 5∶5, 3∶7, 1∶9比例混合的奇异样本红色值目标概率分布。

对被试样本，估计其红色值概率分布，将其划分为与目标概率分布取得最小均方误差所对应的类别。在颜色值域等分区间数量较小时，存在分类误差。当颜色值域等分区间数量大于等于25时，所提方法的分类准确率和召回率达到100%。

进一步的研究包括所提出的方法在更多品质和二元混合比下的有效性，并扩展至更多元的奇异样本。