双边约束下形状记忆合金梁的混沌运动

刘亚妮, 冯进钤, 沈晓娜, 李玉婷, 王迎宵

(西安工程大学 理学院, 西安 710048)

近年来, 碰撞振动系统的研究已引起人们广泛关注. Holmes[1]通过弹跳小球实验, 证明了碰撞振动系统中分岔和混沌运动的存在性； 文献[2]针对一类弹性碰撞振动系统的分岔控制问题, 提出了一种分岔预测及控制方法; 文献[3]研究了分段光滑碰撞振动系统的吸引域结构变化机理; 文献[4]研究了碰撞振动系统中的混沌控制, 从而提高了碰撞振动系统的工作效率.

形状记忆合金(SMA)是一种特殊材料, 具有形状记忆和伪弹性等效应. 基于这些特性, Tanaka[5]建立并分析了一维增量型本构模型; Lagoudas等[6]提出了一种用于SMA伪弹性响应的简化材料模型; 周博等[7-8]给出了形状记忆因子的概念, 并分别从细观力学角度以及宏观力学角度建立了SMA各种相变行为之间的形状记忆演化方程； Savi等[9]研究了形状记忆双杆桁架的动态响应; 张清泉等[10]研究了受轴向载荷的形状记忆合金梁的动力稳定性与混沌运动. 但上述关于SMA的研究均未考虑其迟滞环特性. 文献[11]分析了SMA的应力应变迟滞环特性; 文献[12-13]分别建立了受Gauss噪声激励的振动模型以及形状记忆合金简支梁在受轴向简谐激励和横向白噪声激励时的振动模型; 文献[14-16]研究了平面内随机激励的巨型磁致伸缩薄膜形状的记忆合金复合材料板的非线性动力学特性和最优控制, 以及磁形状记忆合金(MSMA)梁在轴向随机激励作用下的非线性动力学特性和最优控制. 在实际工程中, 形状记忆合金梁通常受双边刚性约束的影响. 基于此, 本文以具有双边约束的形状记忆合金梁模型为研究对象, 利用Melnikov方法得到系统产生混沌的必要条件, 所得结果可用于形状记忆合金梁的混沌控制.

1 双边约束形状记忆合金梁模型

平均密度为ρ、 高度为H、 长度为l、 横截面宽度为b的简支形状记忆合金梁模型如图1所示, 在其基底层的上方和下方均粘着厚度相同的形状记忆合金层, 其中基底层的厚度为d. 该形状记忆合金梁受轴向谐和激励J=j0+jcos(Ωt), 其动力学方程为

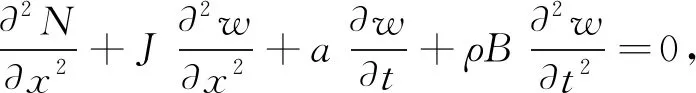
(1)

其中B为合金梁的横截面积,N为其弯矩,w为其横向位移,a为线性阻尼.

该梁受轴向谐和激励时的振动方程为

(2)

其中

图1 简支形状记忆合金梁模型

图2 形状记忆合金梁在双边约束下的截面

形状记忆合金梁在双边约束下的截面如图2所示, 其中形状记忆合金梁左右两侧的约束均为一U形槽. 在该约束条件下, 系统(2)的运动方程为

(3)

(4)

其中R为碰撞恢复系数, 一般描述为R=1-ξr0, +表示碰撞前的时刻, -表示碰撞后的时刻，g为线性刚度系数,δ为非线性刚度系数,τ为阻尼系数,ζ为负阻尼系数,f为谐和激励幅值.

2 未扰系统的同宿轨

令式(4)中ξ=0, 得到未扰系统方程

(5)

(6)

Hamilton函数为

(7)

图3 未扰系统(5)的轨线

当g=2.0,δ=2.0,h=1时, Hamilton量取不同值时未扰系统(5)的轨线如图3所示, 其中实线表示鞍点S的2条同宿轨.

根据H(m,n)=0, 推导出未扰系统同宿轨为

(mh(t),nh(t))T=

(8)

其中

T±表示同宿轨到达约束面的时间.

3 Melnikov函数

利用Melnikov理论[17-18], 系统(4)的Melnikov函数可表示为

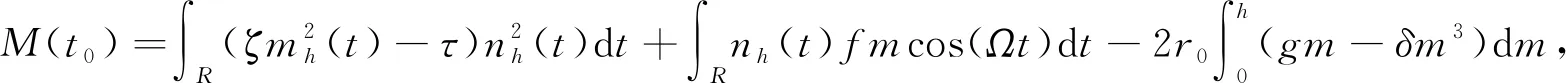
(9)

简化为

M(t0)=ζU1+τU2+fU3+r0U4,

(10)

其中

令

则

U3=2sin(ωt0)[sin(ωT0)W1-cos(ωT0)W2],

利用Melnikov理论, 系统(3)出现Smale马蹄混沌的必要条件为

(11)

4 数值模拟

为验证解析结果式(11)的正确性, 考虑不同约束位置情况下谐和力以及碰撞恢复系数对该系统混沌运动的影响. 令系统参数g=2.0,ω=2.2,δ=2.0,τ=0.15,ζ=0.015,ξ=0.1, 当式(11)取等号,h=1.0,1.1,1.2时, 系统的Melnikov临界线如图4所示, 其中线下为可能的混沌区域, 线上为非混沌区域. 由图4可见,h越大系统产生混沌解所需的碰撞恢复参数r0越大, 且临界值f随r0的增大而增大, 即较大的谐和力可促进混沌产生.r0越大系统损耗的能量越大, 更大的谐和力有助于2个势阱间的跃迁运动, 预示混沌运动的发生. 基于式(11)的临界条件, 当h=1.0,r0=2.0时, 得到临界值f≈4.1.

为验证上述结论的正确性, 在图4临界值下方取点A(4.0,2.0), 绘制在A点参数条件下系统的相图(图5中曲线)和Poincaré截面图(图5中黑点), 其中图5(A)初值(m,n)T=(-0.01,-0.01)T, 图5(B)初值(m,n)T=(0.01,0.01)T. 由图5可见, 在A点参数条件下, 系统做稳定的周期3运动, 对应的最大Lyapunov指数λ≈-0.12, 表明系统在该参数条件下做非混沌运动.

图4 Smale马蹄混沌生成的临界线

图5 f=4.0时系统(3)的相图和Poincaré截面图

在图4临界值上方取点B(7.0,2.0), 绘制在B点参数条件下系统的相图(图6中灰线)和Poincaré截面图(图6中黑点), 其中图6(A)初值(m,n)T=(-0.01,-0.01)T, 图6(B)初值(m,n)T=(0.01,0.01)T. 由图6可见, 在B点参数条件下, 系统运动杂乱无序, 对应的最大Lyapunov指数λ≈0.26, 表明系统在该参数条件下做混沌运动.

为进一步研究h与r0对系统运动状态的影响, 当f=7.0,h=1.0,1.1,1.2时, 系统最大Lyapunov指数随r0的变化曲线如图7所示. 由图7可见, 随着r0的增大, 最大Lyapunov指数由大于0逐渐变为小于0, 表明增大碰撞参数可抑制系统生成混沌. 在3个不同约束值中,h=1.1的曲线波动幅度较小, 其他两条曲线波动幅度较大, 表明约束值不同, 对系统混沌生成的影响也不同.

图6 f=7.0时系统(3)的相图和Poincaré截面图

图7 不同h值下最大Lyapunov指数随r0的变化曲线

综上, 本文基于非光滑系统的Melnikov方法, 研究了在轴向谐和激励下双边约束简支形状记忆合金梁的混沌运动, 得到系统具有混沌解的必要条件, 并利用数值仿真方法验证了该解析结果的有效性和正确性. 研究结果表明, 当系统参数取特定值时, 谐和激励幅值越大, 系统越容易做混沌运动, 但增大碰撞恢复系数可抑制混沌产生.