XGBoost启发的双向特征选择算法
2021-05-26刘兆赓李占山
王 丽, 王 涛, 肖 巍, 刘兆赓, 李占山
(1. 长春工业大学 计算机科学与工程学院, 长春 130012; 2. 吉林大学 人工智能学院, 长春 130012; 3. 吉林大学 计算机科学与技术学院, 长春 130012)
特征选择是机器学习领域中的一个重要问题, 可通过缩小特征维度提高模型的精度及运行速度, 减少运行时间. 在寻找最优特征子集过程中, 通过结合一些搜索策略去除冗余特征与不相关特征, 目的是在给定的泛化误差下选择维度最小的特征子集, 或者选择具有K个特征的最佳特征子集, 使其在原始样本上产生最小的泛化误差[1].
由于特征的选取方式与评价方式不同, 因此特征选择方法又分为过滤式方法、 包裹式方法及嵌入式方法[2]. 过滤式方法通常依赖于数据的固有属性, 如方差、 熵、 相关性等估计特征子集的重要程度, 不依赖于特定的学习器, 通常速度较快并具有可伸缩性[3]. 包裹式方法通过一些已有的机器学习算法评估所选的特征子集, 评估过程依赖于这些机器学习算法并与之不断交互, 通常产生的结果较好[4]. 嵌入式方法将特征选择过程融入学习过程中, 通过优化预先设计好的目标函数搜索最优特征子集, 并在学习过程中删除对分类结果影响较小的特征, 保留良好特征[5].
由于搜索空间会随着特征个数的增加呈指数级增长, 所以在分类问题中的特征选择是NP难问题. 对于包含n个特征的问题, 其搜索空间会有(2n-1)种可能的结果[6-7]. 目前, 对特征选择方法已有许多研究成果, 在分类问题中, 不同搜索策略产生的最优特征子集也不同, 因此也可分为穷举法、 随机方法以及基于启发式的特征选择方法等. 穷举法试图完全搜索特征空间以找到一个能正确区分所有类别的最小特征集合. 但当数据的特征个数较多时, 在时间和空间上很难计算和评估所有的特征子集, 因此在包含大量特征的数据集中很少用穷举法. 基于启发式的特征选择算法有定向搜索算法、 分支界限法、 最优优先搜索算法等[8]. 这些算法能在保持模型精度的同时找到最佳的特征子集[9]. 这类算法的优点是具有良好的时间复杂性, 特别是基于演化计算的方法由于其超强的全局搜索能力在特征选择问题中受到广泛关注[10]. 如文献[11]提出了通过基于特征的熵信息生成切割点序列表, 寻找最佳切点组合进行特征选择的改进离散化粒子群优化算法; 文献[12]给出了以特征为顶点、 以特征相关性为边构造无向图, 并将无向图导出为最小生成树, 通过处理最小生成树的方法进行特征选择.
集成学习是解决机器学习问题的重要方法之一[13], 本文受基于决策树的集成学习中极端梯度提升算法(XGBoost)的启发, 提出一种新的特征选择算法BSXGBFS(bidirectional search based on XGBoost for feature selection). 该算法首先考虑将XGBoost算法中用于构建集成树模型的指标选为特征选择问题中单个特征的重要性度量指标, 然后提出一种新的双向搜索策略更好地权衡如何使用多个特征重要性进行特征选择, 最后给出新算法BSXGBFS理论上的时间复杂度上界.
1 预备知识
1.1 特征选择问题
特征选择问题可描述为: 对于给定N个样本D个维度特征的数据集DataSetN×D, 特征选择任务就是从D个维度特征中选取d个特征(d≤D), 使得目标函数J(S)取最大值, 其中SubDataSetN×d是DataSetN×D的一个特征子集, 简记为S. 优化目标J一般为模型的分类准确率、 维度缩减率或二者的结合. 即特征选择的目的是通过选取特征数量尽可能少的特征子集S使得目标函数J(S)最大化. 求解特征选择问题时, 通常采用如下二进制编码方式将第i次选取的d维特征子集扩展到D维:

(1)

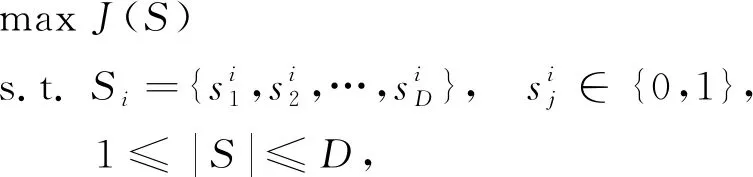
(2)
其中|S|表示在特征子集S中选取的特征数量.
1.2 XGBoost算法
极端梯度提升算法XGBoost是一种基于树的Boosting算法[14]. XGBoost算法相比于传统的梯度提升决策树算法, 创新性地利用了损失函数的二阶导数信息, 使得XGBoost算法能更快收敛, 保证了较高的求解效率, 同时还增大了可扩展性, 因为只要一个函数满足二阶可导的条件, 则在适当的情形下该函数便可作为自定义的代价函数而被使用. XGBoost算法的另一个优点是其借鉴了随机森林算法中的列抽样方法, 进一步降低了计算量和过拟合. 目前, XGBoost算法被广泛应用的原因不仅在于其训练后的模型表现好、 速度快, 能进行一些数据规模较大的计算, 而且其既能解决分类问题, 还能很好地处理回归问题[15].
XGBoost算法可表示为
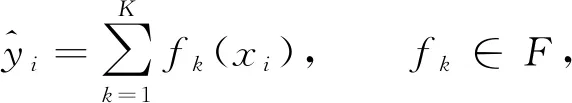
(3)
其中K表示树的棵数,F={f(x)=ωq(x)}(q:m→T,ω∈T)表示模型的函数空间,fK(xi)表示第i个样本在第K棵树中的分类结果. 由XGBoost算法的表达式可见, 该模型是迭代残差树的集合, 每次迭代时都会增加一棵树, 每棵树通过学习前(N-1)棵树的残差, 最终构成由K棵树线性组合而成的模型.

对任意结构确定的树, 有
其中C是所有树用于产生节点时使用的特征集合, GainC是每棵树用C中特征分割后产生的增益值, CoverC是树用C中的特征分割时落在每个节点的样本个数.
2 BSXGBFS算法设计
2.1 双向搜索策略
为能在特征选择问题中算法性能更好, 本文结合经典的前向特征选择和后向特征选择方法的优势, 提出新的双向搜索策略, 步骤如下:
1) 前向添加过程. 首先, 设空集为初始状态的特征选择目标集合, 并将候选子集中的全部特征根据式(4)~(6)中的一个重要性衡量标准A1进行评价并排序. 其次, 依次从中选择重要性高的特征添加到目标集合中, 并对加入新特征后的特征集合进行评价, 保留能提高分类准确性的特征. 经过若干次执行后, 得到初步的目标特征子集. 这种方法的优势是根据已经评价好的特征重要性度量结果做启发式, 能给出一个特征选择的方向, 即初步选定一个较好的搜索空间.
2) 后向筛除过程. 将步骤1)中得到的初步目标特征子集再根据式(4)~(6)中的另一个特征重要性指标A2或A3评价后的结果筛除一个最不重要的特征, 进一步提高分类准确性. 经过若干次执行后, 最终得到一个分类准确率较高且特征数目较少的特征子集. 这种方法能保证通过另一个特征评价指标进一步综合衡量出单个特征的实际重要程度, 进而保证删除冗余特征.
2.2 BSXGBFS算法描述
BSXGBFS算法进行特征选择主要包含两个过程: 构造迭代树模型和双向搜索策略. XGBoost算法中定义的整体损失函数为
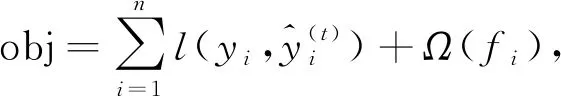
(7)

(8)
为降低树分割后的损失, 根据各子节点的权值进一步计算不同特征作分割点后带来的增益Gain, 有

即作分割点的特征产生的增益可表示为: 该特征节点左右分支的子节点总权值之和与用该特征作分割点前总权值之差.
先根据式(4)~(6)分别计算3种特征重要性, 并得到对应的特征重要性评价集合A1,A2,A3, 然后从这3个集合中选择2个, 作为执行双向搜索策略的特征评价集合. 在实际操作中, 会有6种可能的排列结果, 因此可利用多核CPU的优势一次性并行完成计算, 缩短计算时间, 并使结果趋于最优.
BSXGBFS算法的伪代码如下.
算法1BSXGBFS算法.
输入: Original feature setA;
输出: Objective feature setO;
O← Ø
depth ← 0
Initialization the three measures of feature importance Fcount, AvgGain, AvgCover
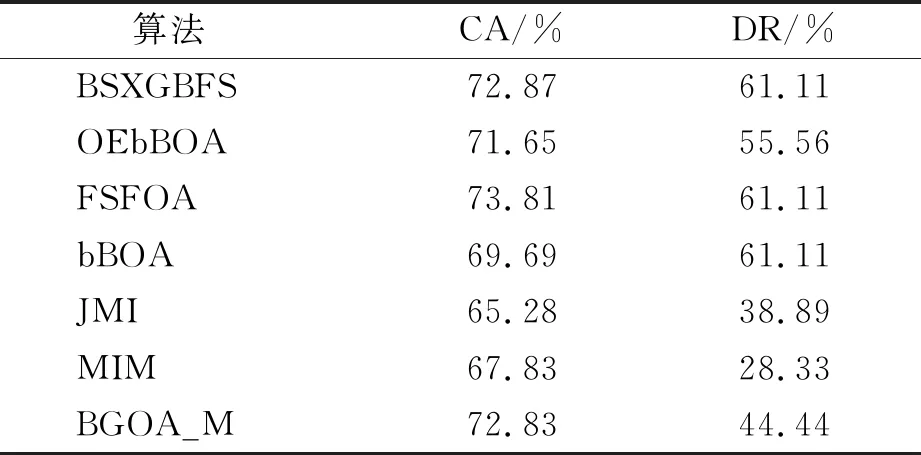
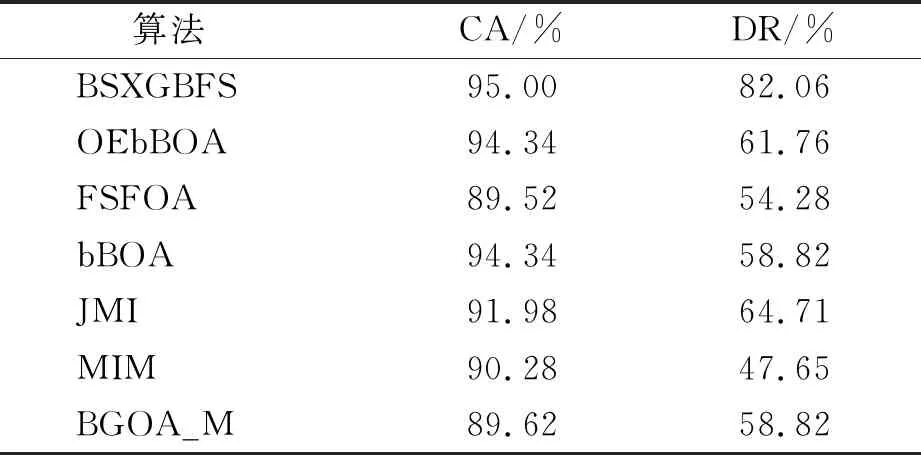
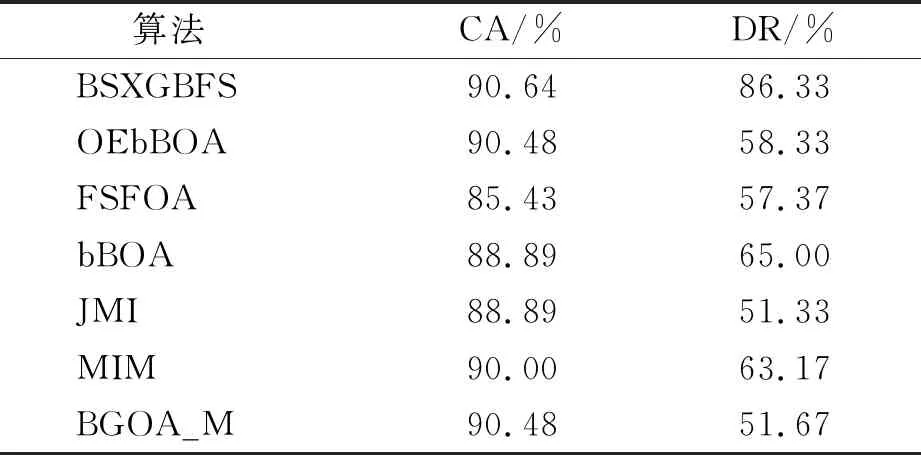
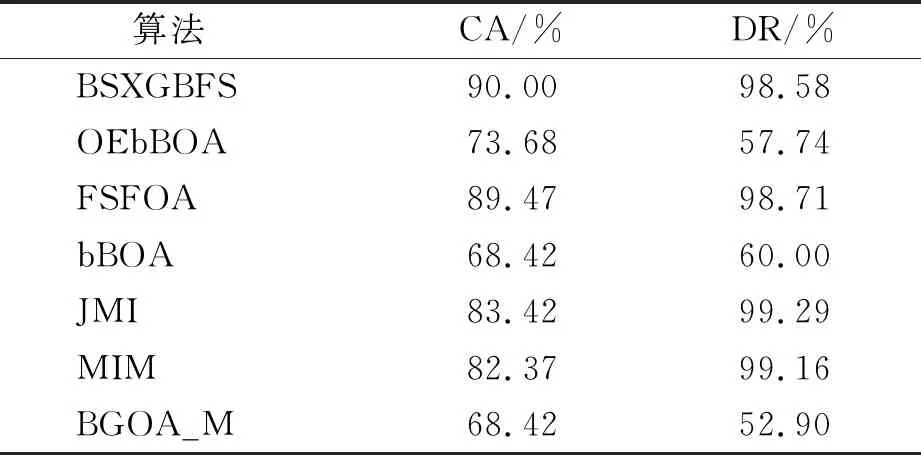
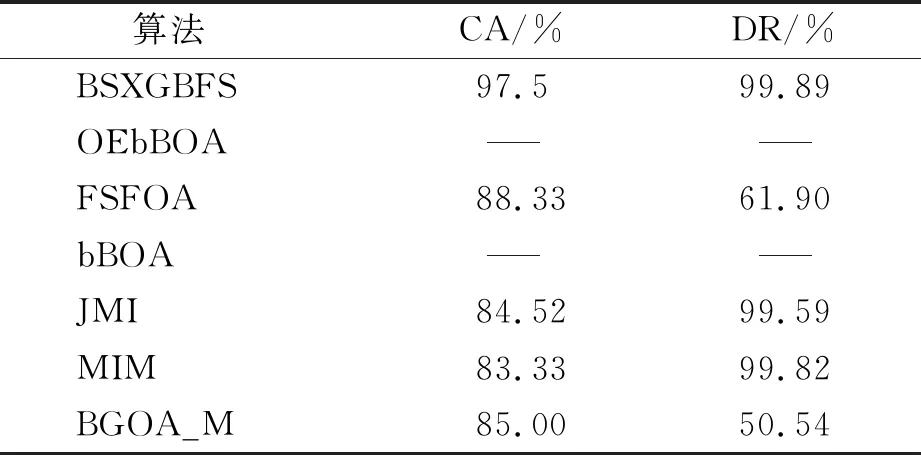
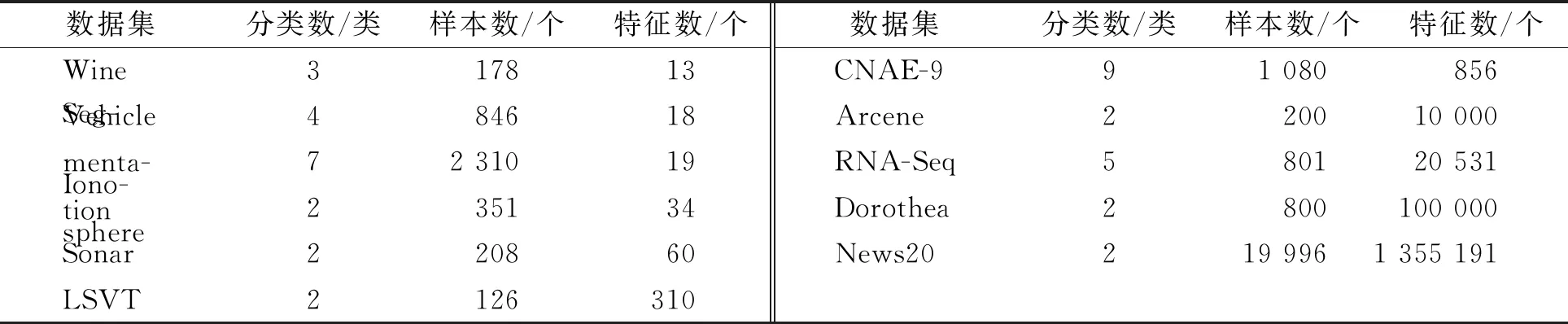
while depth for a inAdo Calculus the best feature segmentation pointak Generate left child node and right child node depth ← depth+1 Update ensemble model for tree in ensemble model do for node of tree do Calculate gain and cover generated by node Fcount ← Fcount+1 Gain ← Gain+gain Cover ← Cover+cover forainAdo AvgGain ← Gain/Fcount AvgCover ← Cover/Fcount GetA1from sortingAin descending order according to Fcount GetA2from sortingAin descending order according to AvgGain GetA3from sortingAin descending order according to AvgCover Select two set fromA1,A2andA3randomly, then rename them asB1andB2 ReverseB2 forbiinB1do O′←O∪bi ifJ(O′)>J(O) then O←O′ forbjinB2do ifbjinO O′←O-bj ifJ(O′)>J(O) then O←O′ returnO. O(MNlgN+MNKD+mlgm+2mT). 实验选择目前应用最广泛的UCI(UCI machine learning repository)数据库中的11个覆盖低维到超高维的标准数据集, 各数据集信息列于表1. 实验选择多策略二元蝴蝶优化特征选择算法(OEbBOA)[16]、 基于森林优化算法的特征选择算法(FSFOA)[17]、 基于蝴蝶优化算法的特征选择算法(bBOA)[18]、 使用联合互信息策略的特征选择算法(JMI)[19]、 使用互信息最大化策略的特征选择算法(MIM)[19]、 基于二元蝗虫优化算法的特征选择算法(BGOA_M)[20]作为与本文算法的对比算法. 实验中全部实验代码使用Python 3.6实现. 实验平台处理器为AMD Ryzen 7 1700, 内存容量32 GB, 硬盘容量2 TB. 表1 UCI的数据集信息 采用多数研究中常用的分类准确率(classification accuracy, CA)与维度缩减率(dimensionality reduction, DR)做实验结果分析的性能衡量指标[21-22]: CA=CN/AS, (9) DR=(AF-SF)/AF, (10) 其中CN表示分类正确的样例数, AS表示全部样例数, AF表示特征总数, SF表示进行特征选择后的特征数. 采用KNN(K=1)作为评价分类准确率的基分类器. KNN分类器具有易实现且参数较少, 能更好地反映特征选择算法自身性能的特点, 因此使用KNN测试特征选择算法的性能, 并用于对比实验[18-22]. 数据集的划分均采用70%的样例作为训练集, 30%的样例作为测试集. 实验结果列于表2~表12. 表2 BSXGBFS及其对比算法在Wine数据集上的测试结果 表3 BSXGBFS及其对比算法在Vehicle数据集上的测试结果 表4 BSXGBFS及其对比算法在Segmentation 数据集上的测试结果 表5 BSXGBFS及其对比算法在Ionosphere数据集上的测试结果 表6 BSXGBFS及其对比算法在Sonar数据集上的测试结果 表7 BSXGBFS及其对比算法在LSVT数据集上的测试结果 表8 BSXGBFS及其对比算法在CNAE-9 数据集上的测试结果 表9 BSXGBFS及其对比算法在Arcene 数据集上的测试结果 表10 BSXGBFS及其对比算法在10 000维内的数据集上分类准确率测试结果 表11 BSXGBFS及其对比算法在10 000维内的数据集上维度缩减率测试结果 表12 BSXGBFS及其对比算法在高维数据集上的测试结果 由表2~表12可见, 对于10 000维以内的数据集, BSXGBFS算法无论是在分类准确率还是维度缩减率上, 都存在较高的竞争力, 甚至在Ionosphere,Sonar,CNAE-9,Arcene这4个数据集上, 分类准确率和维度缩减率性能在全部对比算法中都达到了最优. 因此, BSXGBFS算法不存在如OEbBOA,FSFOA,BGOA_M等基于演化计算的特征选择算法需要过多牺牲维度缩减率换取分类准确率的问题, 而是在确保分类准确率的前提下兼顾了维度缩减率, 也进一步验证了采用特征重要性评价作启发式的合理性. 由表12可见, 在使用RNA-Seq,Dorothea,News20这3个数据集对BSXGBFS算法进行极限测试的过程中, 发现BSXGBFS算法具有可以进一步计算10 000维以上高维数据集的能力, 甚至在10万维Dorothea数据集和100万维News20数据集上都具有可计算性. 实验结果表明, BSXGBFS算法的性能与预期相符, 不仅在中低维数据集上的性能良好, 而且在高维数据集上也具有可计算性. 综上所述, 本文受集成学习算法XGBoost的启发, 提出了一种适用范围更广, 能处理高维数据的特征选择算法BSXGBFS. 对比实验结果表明, BSXGBFS算法不仅在中低维数据集上相比于其他算法更具竞争力, 同时在高维甚至超高维数据集上也具有良好、 可靠的计算能力.2.3 时间复杂度分析
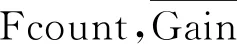
3 实验设计与分析
3.1 实验设计
3.2 实验分析