基于RLS-DLUKF算法的锂电池SOC预测方法研究

朱 磊，刘子博，李路路，潘庭龙，杨玮林

（江南大学物联网应用技术教育部过程研究中心，江苏 无锡214122）

准确地预测锂电池的SOC 值是保证电池高效使用、能量合理分配的必要条件，是实现风光等可再生能源持续利用、提高锂电池组电量均衡程度、保证电动汽车稳定运行[1]的重要前提。经典预测法、数据预测法和耦合算法预测法等是当下普遍使用的SOC估计策略。

常见的经典预测法包括安时积分法[2]、开路电压法[3]、阻抗谱法[4]等。安时积分法在计算过程中会不断累积误差并且无法将初始误差优化，预测精度较低；开路电压法在使用前后需要将电池静置一段时间且静置时间长短对测量的精度有很大影响，一般只适用于实验室等特定环境下对电池SOC 的测量；阻抗谱法的测试环境较为苛刻，需要建立复杂的函数方程并查表获得所需SOC 值，该方法计算复杂、工作量大且测量精度较低。数据预测法有BP人工神经网络法[5-6]、支持向量机法[7-8]等。BP人工神经网络法的弊端是精确的预测需要以足够多的数据为支撑，同时训练策略的不同会导致估算值出现较大的差异；支持向量机法计算复杂，容易存在过拟合问题。常见的耦合算法是将某一种算法和卡尔曼滤波算法的耦合，如使用自适应方法优化扩展卡尔曼滤波噪声协方差矩阵的自适应扩展卡尔曼滤波算法[9]、利用无迹卡尔曼滤波(UKF)[10]算法可以优化非线性系统及具有二阶泰勒展开精度的特点与多个模型进行融合的交互多模型无迹卡尔曼滤波[11]算法等。目前耦合算法预测法较为常见，尤其是与UKF 算法的结合使用，既可以获得较为准确的SOC，还可以获得较好的鲁棒性，但在强非线性系统中，UKF算法容易出现估计精度下降、计算速度减缓的问题。

本工作针对在强非线性系统中UKF 算法估计精度低的问题，首先对锂电池进行等效建模，然后通过递推最小二乘(RLS)算法在线识别出该模型的未知变量，并将其作为后续估计算法的输入变量，最后运用基于确定性采样思想的双层无迹卡尔曼滤波(DLUKF)[12]算法快速、准确地预测SOC。最终表明，DLUKF算法预测SOC比单一UKF算法性能更加优越，精确度更高。

1 锂电池的参数辨识

1.1 锂电池等效电路模型

考虑到RC电路反映电池的极化效应和扩散效应时效果良好，且因计算量和计算难度随着RC电路阶数的提高而增大，故建立如图1所示的电路模型。

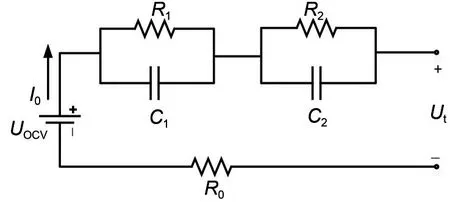
图1 二阶RC等效电路模型Fig.1 Two-order RC equivalent circuit model

电路模型中的电池处于开路状态时对应的端电压为Uocv，模型输出的电压值用Ut表示。电池内部阻值R0的变化是非线性的，电势与基准量存在偏差而产生的极化内阻为R1，相并联的为极化电容C1。用R2表示浓差电阻，相并联的为浓差电容为C2。由图1 可以建立如式(1)所示的电路方程

SOC的定义式为

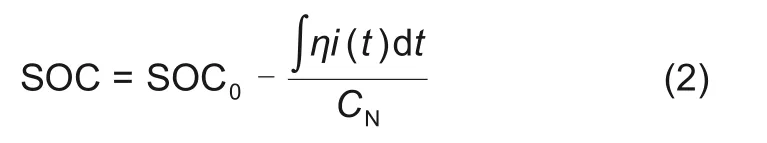
式中，I0为电路电流；SOC0为初始值；η为放电效率；CN为电池的额定容量。联立式(1)、(2)后变换处理可得状态方程

1.2 OCV-SOC特性曲线

本文通过脉冲功率特性实验(hybrid pulse power characteristics，HPPC)来获取OCV-SOC特性曲线，具体实验数据如表1所示。

表1 HPPC实验参数Table 1 HPPC experimental parameters

图2所示为OCV-SOC特性曲线。由图2可知：对比分析上述数据拟合出的六阶、七阶、八阶曲线，七阶曲线拟合效果较好、符合实际情况，对应的拟合函数如下

图2 OCV-SOC特性曲线Fig.2 OCV-SOC curve

1.3 电池模型参数辨识

离线参数辨识[13]的缺点主要是默认模型参数为定值，但电池的系列电阻、电容会在充放电过程中发生变化。如式(5)所示，将RLS 算法的先验估计值加入校正项得到后验估计值，以便在线识别出模型中的变量[14]。

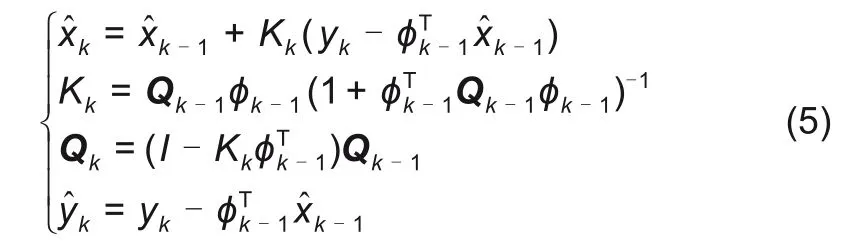
式中，m1、m2、m3、m4为所求模型参数的中间变量，m1=R1R2C1C2，m2=R1C1+R2C2，m3=R0+R1+R2，m4= R0R1C1+ R0R2C2+ R1R2C2+ R1R2C1。

由式(7)化简后的差分方程为

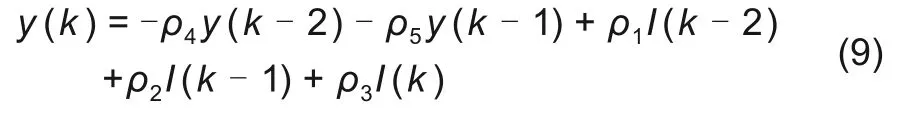
式中，y为输出，y = Uocv- Ut。

待辨识的参数矩阵为

通过联立式(7)和式(9)，通过RLS 算法可得到ρ 的解，再通过式(6)和式(8)即可计算出模型参数R0、R1、R2、C1、C2。

2 基于DLUKF的SOC预测

2.1 DLUKF算法估算流程

将两个UKF 算法内外嵌套形成DLUKF 算法。首先计算内层UKF 算法的时间更新值和量测更新值，得到内层估计值，然后将内层估计值进行加权平均作为外层UKF 算法的时间更新值，并进行外层UKF算法的量测更新，求出所需变量的估计值。DLUKF计算流程[12]如下

（1） 内层UKF算法

Step1：算法初始化。

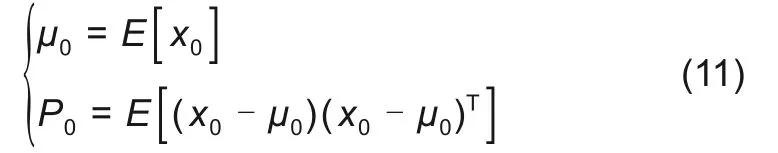
式中，

Step2：在k 时刻，引入基于比例修正思想的对称采样方法获得2n + 1 个采样点{χi,k}，i =0,1,…2n。

均值权值及协方差权值的计算式为

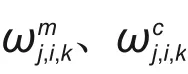
对采样点进行非线性状态函数传递和一步状态预测计算

由式(14)时间更新得到的预测值xi,k+1|k和预测协方差Pi,k+1|k可以产生H个新的带均值权值和协方差权值的采样点{ }ξ'j,i,k+1|k，j =0,1,…H，即量测更新为

采样点更新完成后，对均值权值和协方差权值进行更新

对内层UKF 的估计值进行加权融合，作为外层UKF的初始估计值

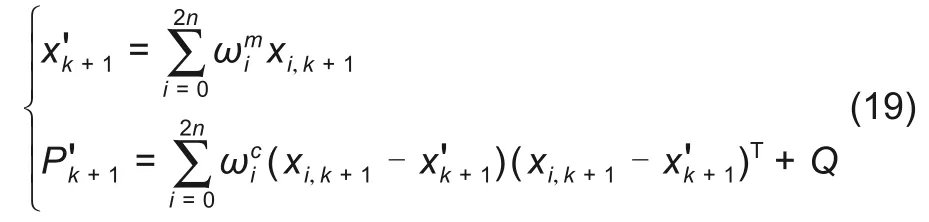
（2） 外层UKF算法

根据step2中选用的采样方法获取2n + 1个采样点{x'i,k+1},i = 0,1,…,2n,以x'k+1和P'k+1为基础进行外层UKF的量测更新

重复计算式(10)～(22)便可得到各个时刻的估计值xk。

2.2 DLUKF估计SOC流程

根据式(3)～(22)可得RLS 算法和DLUKF 算法联合估计电池模型参数及SOC的算法流程为：算法启动前，首先对RLS算法和DLUKF算法给定初值x0和P0，然后通过RLS算法对模型进行参数辨识，状态方程为式(10)，观测方程为式(9)，可得模型参数R0、R1、C1、R2、C2；对于DLUKF算法，状态方程和观测方程在式(3)中体现，其中输入量是电流I0，输出量是电池端电压Ut，通过内层UKF的量测更新得到N个估计初值，然后对估计初值加权融合并输出给外层UKF进行量测更新，最后得到SOC的估计值；接着再通过式(3)获得电池的开路电压Uocv；最后将该开路电压作为系统的一个输入量，进入下一时刻的参数辨识。通过以上方式将RLS算法和DLUKF算法联合形成一个整体的递推结构，实现参数的在线辨识并获得更高精度的SOC估计。

3 实验仿真与分析

3.1 模型参数辨识

本文使用三星INR18650-30Q钴酸锂电池为研究对象进行充放电实验。该锂电池的额定电压为3.61 V，充电终止电压为4.2 V，放电终止电压为2.5 V，最大充电电流为4 A，容量为3040 mA·h，重量为45.6 g，直径为(18.33±0.15)mm。

图3 参数辨识曲线Fig.3 Curves of parameter identification

图3 所示为RLS 算法在线识别五个参数的结果。图3(a)为电池欧姆内阻的变化曲线，在通电初期，电池的欧姆内阻较大且电压波动明显，随后逐渐减小并趋于稳定；图3(b)～(e)分别为极化电阻、极化电容、浓差电阻、浓差电容变化曲线，都随着SOC的降低而不断增大，最终趋于稳定。由图3的参数辨识结果可知：当给定初值不准确时，RLS算法能够及时修正各个参数与真实值之间的误差，并快速收敛到真实值附近。

3.2 UDDS工况下SOC预测

为了验证DLUKF算法在预测SOC时的快速收敛性和极高的预测精度等优点，本文在UDDS工况下分别采用UKF 算法和DLUKF 算法同时结合递推最小二乘法进行SOC 估计，并对两种算法的仿真结果进行对比。图4所示即为UDDS工况下的电流示意图。由图4可见，该工况下电流变化满足强非线性条件。实际测量值曲线的附近。

图4 UDDS工况电流Fig.4 Current of UDDS condition

图5 UDDS工况下锂电池SOC估计曲线Fig.5 SOC estimation curve of lithium battery under UDDS

图6 所示为两种算法估计的SOC 值的误差曲线。由图6 可知：DLUKF 算法估计值的误差均小于2%，平均误差为0.9%；采用单一UKF算法预测的SOC值误差最大约为3%，平均误差为1.3%。

图6 UDDS工况下SOC估计误差Fig.6 SOC estimation error under UDDS

图7所示为两种算法在UDDS工况下测得的电池端电压曲线。图7(a)为使用DLUKF 算法测得的电池端电压，曲线比较光滑，说明该算法跟踪精度高；图7(b)为使用UKF算法测得的电池端电压，曲线电压毛刺较多，对噪声抑制效果较差。

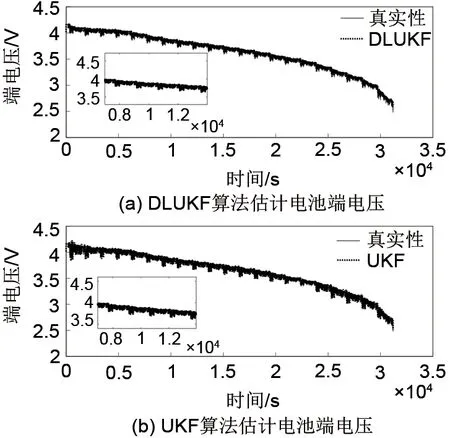
图7 UDDS工况下电池端电压估计值Fig.7 Terminal voltage estimation value under UDDS

图8为两种算法所测端电压的误差曲线。图8(a)为DLUKF所测端电压的误差，误差曲线较为平稳，始终在2%～4%范围内波动，说明DLUKF 算法不仅具有优良的稳定性，还具有较高的跟踪精度，这是由于该算法在在内外层UKF 的作用下，及时对滤波增益矩阵进行了修正；图8(b)为UKF算法测得的端电压的误差曲线，整体波动较大，并且初始误差较大。

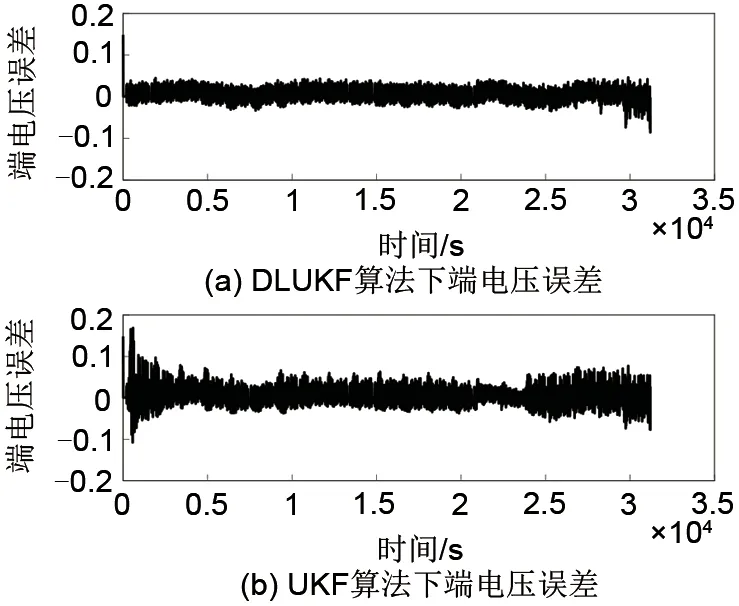
图8 UDDS工况下电池端电压估计误差Fig.8 Terminal voltage estimation error under UDDS

3.3 FUDS工况下SOC预测

为了进一步验证所提算法的有效性，本文通过FUDS 工况对DLUKF 算法和UKF 算法再次进行了分析。图9所示为FUDS工况下电流变化示意图。

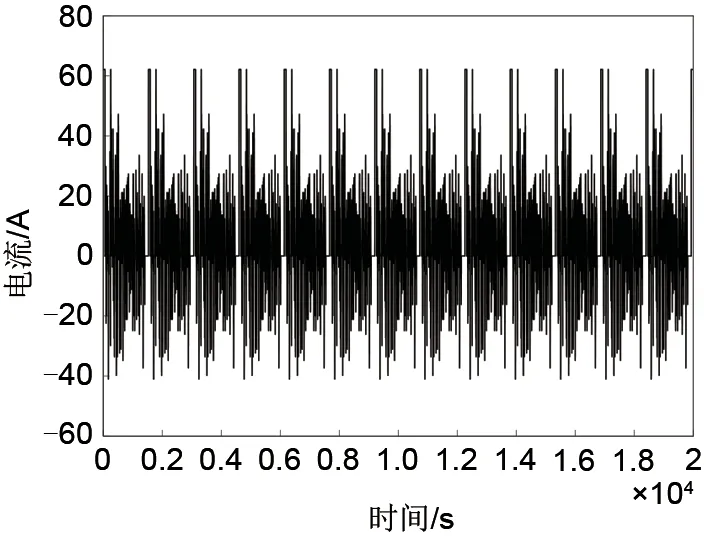
图9 FUDS工况电流Fig.9 Current of FUDS condition

图10 所示为FUDS 工况下两种算法SOC 估计值与真实值之间的比较。由图10 可知，当给定初值与真实值存在差异时，DLUKF 算法很快跟踪到真实值附近，而UKF算法则变化较为缓慢。

图11 所示为在FUDS 工况下两种算法对SOC预测的误差。从图中可知，DLUKF 算法预测SOC的误差在2%左右，UKF算法的误差在2%～4%之间。同时，由仿真结果可得，DLUKF 算法的平均误差为0.8%，采用单一UKF算法所预测SOC的平均误差为1.05%.

图12所示为DLUKF算法和采用单一UKF算法在FUDS 工况下所测端电压曲线。图12(a)为DLUKF 算法估计端电压曲线，从放大曲线可以看出，该曲线较为光滑、平稳，说明稳定性较好，跟踪精也很高；图12(b)为采用单一UKF 算法所测端电压曲线，从放大曲线可以看出，该曲线毛刺较多，没有紧密跟随在真实值附近，说明其跟踪精度较低，对噪声的抑制效果较差。

图10 FUDS工况下锂电池SOC估计曲线Fig.10 SOC estimation curve of lithium battery under FUDS

图11 FUDS工况下SOC估计误差Fig.11 SOC estimation error under FUDS

图12 FUDS工况下电池端电压估计值Fig.12 Terminal voltage estimation value under FUDS

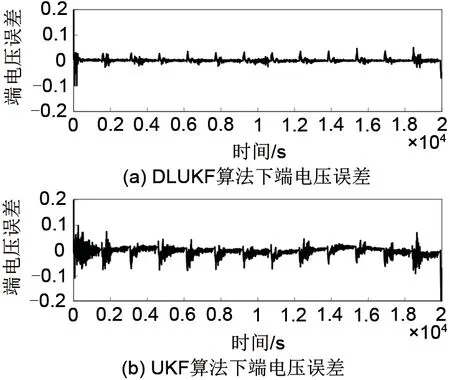
图13 FUDS工况下电池端电压估计误差Fig.13 Terminal voltage estimation error under FUDS

图13 为两种算法所测端电压误差曲线。由图可知，相对于UKF 算法，DLUKF 算法所测端电压误差更平稳，说明其稳定性较好、跟踪精度更高。

4 结 论

为了能够在复杂多变的工况中更准确地预测电池SOC，本文提出一种基于RLS-DLUKF算法的锂电池SOC 预测方法，在UDDS 工况和FUDS 工况下进行分析对比，得到结论如下。

（1）DLUKF 算法和UKF 算法都能够很好地预测锂电池的SOC。

（2）在不同的复杂工况下，如锂电池电流变化剧烈的情况下，UKF 算法对SOC 的预测容易出现稳定性较差、不能及时修正初始误差的情况；而DLUKF 算法在双层UKF 的作用下，能够快速、稳定地纠正给定值，更精确地预测出钴酸锂电池的SOC。

（3）综上分析，DLUKF 算法比UKF 算法更适合于锂电池SOC的预测。