高阶思维培养取向的信息技术有效应用研究
2021-05-26周雪花
周雪花
摘要:为进一步提高学生高阶思维的应用能力与培养学生高阶思维的有效性,文章提出基于信息技术构建高阶思维培养的初中数学课堂教学。在传统数学教学模式无法满足新课标发展要求的基础上,积极探索与研究了现阶段我国初中数学教学方式与教学理念,研究得出通过科学信息技术构建初中数学教学课堂对培养学生高阶思维发展具有实质意义。研究中:为进一步论证信息技术在高阶思维培养取向的可行性,以《幾何画板》为教学工具搭建了九年级数学课堂教学。
关键词:高阶思维培养;信息技术;数学课堂
中图分类号:G633.6文献标识码:A文章编号:1992-7711(2021)25-0075
高阶思维泛指在学习过程中通过自身理论与多元视角对数学知识的理解与重构而形成“高阶学习”的一种思维模式。基于构建主义视角分析高阶思维可将其定义为主动、意图、重构、真实及合作五维因素,这五个因素与特征在高阶思维中并非独立,而是通过协同、共生、交织后催化对事物的理解与再塑,通过高阶思维的培养,学生可以进一步提高数学知识理解能力,对培养学生的数学核心素养而言具有现实意义。
一、依托《几何画板》,加强学生知识理解
《几何画板》是近年来我国初中、高中数学教学中广泛运用的一款计算机工具性软件,相比传统信息技术与教学工具,《几何画板》具有实时性、工具性、灵活性及直观性的教学特点,从绘制、呈现、分析与研究,可进一步提高学生理解题意的能力,从而实现多元情境下的正确识别。此外,通过几何画板展示各种不同的情况,让学生观察、思辨,达到自主得出结论的目的。以《二次函数》题为例:已知二次函数y=x2-x+n,如抛物线与y轴相交于点A,过A作AB∥x轴交抛物线于另一点B,当S△AOB=4,求二次函数的解析式。
分析:在讲解分析的过程中,数学教师可利用《几何画板》与多媒体教学相结合的方式培养学生的高阶思维。首先,可通过多媒体视频回顾二次函数的性质,进而依托《几何画板》将二次函数y=x2-x+n的图像及y=x2-x+n和y轴交点的坐标A(0,n)展示出来,在学生观看后,再运用多媒体将过A作AB∥x轴交抛物线于另一点B,根据二次函数性质可知B(1,n),通过《几何画板》的展示,让学生对解题步骤及所需求的点的坐标值加深理解,进而得出答案。
根据以上结论,将《几何画板》运用到二次函数教学中,可以把抽象的知识点形象化,帮助学生直观地理解,加深学生对二次函数的理解,通过多媒体信息技术的辅助教学,使原本枯燥乏味的数学课堂变得充满趣味性。
二、依托《几何画板》,搭建小组合作学习模式
利用小组合作组织课堂讨论,教师可以在教学内容展开之前,引导学生用引导题引导学生检验讨论结果。例如:如图1,在《圆周角定理》课中,教师可以通过《几何画板》绘制,通过变换B、C两点的位置,以小组合作讨论的方式引导学生根据观察、比较、分析同弧所对的圆周角和圆心角的关系,加强中学生的逻辑推理能力,提高他们的观察能力,促使学生具备良好的识图能力。这种开放性、互动式的讨论活动,可以有效地增强学生的合作意识,使学生在潜移默化中完善自己的数学能力,并拓展学生的思维发展。
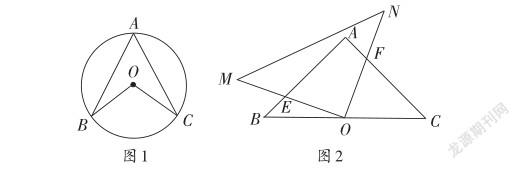
又如图2,两个全等的等腰直角三角形ABC和OMN,AB=3,点O为边BC的中点,△OMN绕着点O顺时针旋转,旋转过程中边OM,ON分别交边AB,AC于点E,F。1.在旋转过程中,线段AE与CF有什么数量关系?2.在旋转过程中,线段OE与OF有什么数量关系?3.在旋转过程中,四边形AEOF的面积变化?4.在旋转过程中,求△AEF的面积的最大值?
在解决这个问题的过程中,每一小问都通过几何画板演示,帮助学生找到解题的关键点,直接在几何画板上添加辅助线,更好地理解题意,从而快速解题。
通过小组合作学习模式与信息技术的融合,不仅可以提高学生学习的积极性,也可以活跃课堂气氛。在讨论过程中,教师要注意梳理、引导等问题,如学生在讨论过程中出现偏差。教师要主动梳理自己的思路,加强学生对教学知识的理解。这种讨论方式不仅可以提高学生思维的活跃度,而且可以有效地调动学生的主观能动性,通过学生讨论的形式,对教学内容有大致的了解,加强学生内化知识的效率和质量,有效激发学生参与数学教学的兴趣。此外,教师可以在学生积极讨论的基础上,开展小组合作讨论活动,增强学生的讨论兴趣,培养学生思维的发展,促进学生逻辑思维的形成,加速数学建模。
三、结论
综上所述,利用《几何画板》的基本功能来表现概念的“形态学”方法,能有效地加深学生对概念的理解和认识,对培养学生高阶思维具有现实意义,一方面避免学生因图形错误而出现错误,另一方面,可将抽象的知识点转化为形象化,帮助学生直观理解。
参考文献:
[1]张美婷,刘秋芳.转变复习模式促进学生高阶思维发展[J].中小学教学研究,2019(11):72-76.
[2]陈明.几何画板在数学新知拓展环节应用的课例研究[J].中小学教学研究,2017(3):7-10.
[3]吕云彬.让学生在“思考”的课堂中体会学习的快乐——一节初三数学复习课“二次函数中的面积问题”带来的思考[J].中小学教学研究,2014(7):54-56.
(作者单位:广东省珠海市第十中学519070)