基于微观机制的复杂应力状态下钢材韧性断裂行为研究

叶继红，范志鹏

(1. 江苏省土木工程环境灾变与结构可靠性重点实验室(中国矿业大学)，徐州 221116；2. 徐州市工程结构火安全重点实验室(中国矿业大学)，江苏，徐州 221116；3. 东南大学土木工程学院，江苏，南京 211189)

目前，金属材料断裂预测方法总体可分为两类：一类为传统断裂力学方法[1]；另一类为基于微观机制的断裂预测方法[2]。由于传统断裂力学方法是基于材料中已存在宏观裂纹假定，其不适用于无初始缺陷的韧性断裂问题。基于微观机制的断裂预测方法是根据金属材料的微观机理建立力学模型，其认为引起材料断裂的两种主要微观机理为空穴聚合型断裂机理及局部剪切带的形成。

空穴聚合型断裂机理是钢材韧性断裂的常见形式，空穴演化过程通常分为三个阶段：空穴形核、空穴扩张和空穴贯通[3-4]，如图1 所示。金属材料在低应力三轴度下断口部位会呈现剪切型微观断裂机理[5-7]，与脆性断裂形式不同的是材料在形成剪切型断裂前可承受明显的塑性变形。如图2所示，在低应力三轴度应力状态下，材料中空穴在形核后不仅没有扩张的趋势，相反空穴体积会随着塑性应变的增大而逐渐变小，直至突然压扁形成塑性剪切带[8]，引发剪切断裂。

图 1 空穴形核、扩张及贯通机理Fig. 1 The mechanism of void nucleation,expansion and penetration

图 2 塑性剪切带Fig. 2 Plastic shear band

基于微观机制的断裂预测模型在预测钢材延性断裂上具有明显优势，如Rice-Tracey 模型[9]、VGM 模型和SMC 模型[10]、GTN 模型[11]等，近年来这些模型开始广泛应用于钢材韧性断裂破坏研究。廖芳芳等[12-13]进行了多组Q345 钢材切口圆棒单轴拉伸试验，并采用校准后的VGM 模型和SMCS 模型对Q345 钢焊接节点的断裂行为进行预测，预测结果较好；黄学伟等[14]采用GTN 模型对梁柱焊接节点的断裂行为进行预测，得到了良好的预测结果。上述断裂模型应用于应力三轴度较高的钢材断裂行为预测时可获得较高的精度，但应用于以剪切断裂为主的低应力三轴度区时精度却相对很低，数值模拟结果离散型也较大。其原因是上述断裂模型没有考虑罗德角的影响，在低应力三轴度区的金属材料韧性断裂应变不再符合高应力三轴度区的拉伸断裂趋势。

为了改进上述模型的局限性，马昕煦等[15]在Rice-Tracey 模型基础上提出了一个罗德角依赖型的断裂模型，并将该模型用于钢管节点断裂预测分析，能够准确模拟钢管节点的剪切型断裂行为；黄学伟等[16]在VGM 模型中引入罗德参数的影响提出LVGM 模型，并用校准后的LVGM 模型对一组Q235B 钢节点试件进行断裂预测，预测结果与试验结果吻合良好。上述改进后的断裂模型虽然考虑了罗德角对材料断裂性能的影响，但仍缺乏微观断裂机理支持。闫伸[8]提出了考虑空穴形核的剪切断裂模型VNISFM 模型，并进行了多组材性试验验证了该断裂模型，弥补了现阶段低应力三轴度断裂模型缺乏微观断裂机理支持的局限性。但VNISFM 模型仍存在模型参数较多、校准工作量大的不足。

综上所述，国内外学者已对金属材料的断裂预测方法进行较多研究，但这些研究主要集中在材料处于单一高应力三轴度或低应力三轴度应力状态下，对复杂应力状态下的钢材断裂性能研究尚不充分。本文采用理论模型、有限元分析和断裂试验相结合的方式，对文献[8]的钢材韧性断裂模型进行了改进。采用Fortran 语言将断裂模型编写USDFLD 子程序，将其植入有限元程序ABAQUS，预测了十字型节点试件在复杂应力状态下的断裂破坏过程，验证了本文断裂模型的正确性。

1 应力状态表征

在复杂应力状态下，钢材的韧性可由材料断裂前承受的等效塑性应变(下文称为断裂应变)衡量。钢材在断裂前可承受的等效塑性应变越大，钢材的韧性越好，抵抗断裂的性能越强[17-18]。

为定量考察应力状态对钢材断裂应变的影响，需要引入应力空间概念。对于各向同性材料中任意一点P，引入主应力坐标系(σ1，σ2，σ3)，如图3 所示。直线OZ为静水轴，过原点且与静水轴垂直的平面为π 平面。θ 称为罗德角[19]，标志P点在π 平面上的投影位置(0≤θ≤π/3)。

图 3 材料点的应力状态Fig. 3 Stress state of material point

以O为原点，以静水轴为z轴，建立柱坐标系，主应力状态OP可由一组柱坐标(γ，ρ，θ)表示。由于γ、ρ 的值会随坐标轴位置的改变而变化，在韧性断裂研究中为便于建立塑性本构关系，通常采用等价坐标不变量(I1，J2，θ)表征一点的应力状态。其中，I1为应力张量的第一不变量，J2为应力偏张量的第二不变量。

等效应力σeq是三维应力状态向一维应力状态的一种数值等效，对钢材通常可取为von Mises 应力，如式(1)；应力三轴度T定义为静水应力与等效应力之比，如式(2)；罗德参数L定义为第二主应力位于第一、三主应力之间的相对位置关系，与罗德角θ 呈正相关，如式(3)。

2 韧性断裂模型的构建

2.1 体胞分析方法

钢材是一种宏观连续材料，可近似看作是由大量完全相同的代表性体积元(体胞)紧密堆积在一起构成。为研究这种材料变形、损伤和断裂的力学行为，可通过对简单的体胞模型进行分析[3]，从而将细观尺度上体胞基体材料与空穴共同作用得到的力学响应转化为宏观尺度上材料的整体材性。体胞模型的选取取决于空穴空间排列假定，其中最常用的假定为立方体胞模型。如图4 所示，钢材可看作是由图中完全相同的立方体胞堆积构成，且立方体胞中心含有一个球形空穴。

图 4 立方体胞模型Fig. 4 Cube cell model

体胞模型分析重点在于计算空穴体积百分比fvoid、等效应力σeq及宏观等效应变εeq。立方体胞模型中心含有单个形状为球体的空穴，根据其三重对称性，取体胞的1/8 进行有限元分析，建立主方向为(x，y，z)的直角坐标系，如图4 所示。

在ABAQUS 软件中建立立方体晶格体胞模型，如图5 所示，模型单元采用三维实体单元(C3D8R)。体胞的基体材料选用典型的Q345 材料，幂强化系数n=0.22，弹性模量和泊松比分别为E=205 000 MPa 和ν=0.3。体胞模型基于空穴的空间周期性分布而建立，在任意变形历程中三个外表面均需保持平面且平行于初始外表面，如图6 所示。

对立方体胞模型进行加载时，需要使体胞的应力三轴度T和罗德参数L在变形过程中保持为恒定常数，因此本文采用基于弧长法的ABAQUS/Riks 分析步进行加载。荷载以表面压强的形式分别施加于三个外表面，从而达到应力三轴度T和罗德参数L在变形过程中保持不变的目的。

图 5 立方体胞有限元模型Fig. 5 Cube Cell Finite Element Model

图 6 立方体胞模型边界条件Fig. 6 Cube cell model boundary conditions

2.2 体胞分析结果

2.2.1 高应力三轴度

对于高应力三轴度区(T≥0.5)，选取应力三轴度T在[0.6，3.0]、罗德参数L在[-1.0，1.0]范围内，共15 组不同的应力状态进行体胞模型分析。

以应力状态(T=2.0、L=-1)为例，图7 显示了体胞模型随塑性应变发展的演化过程。从图中可以看出，空穴随着塑性应变的发展逐渐长大，当塑性应变εeq达到0.3 时，相邻空穴间几乎已无基体材料，此时体胞失效。因此，高应力三轴度下体胞失效机理为相邻空穴贯通。

图 7 体胞模型随塑性应变发展演化过程(T=2.0、L=-1)Fig. 7 Somatic cell model evolution process (T=2.0, L=-1)

图 8 等效应力-应变关系Fig. 8 Equivalent stress-strain relationship

图8 显示了体胞等效应力-等效应变关系曲线，图中等效应力下降的拐点可看作体胞失效的临界点[20]。从图中可以看出：1)随着应力三轴度T增大，应力三轴度T相同的3 条曲线越来越接近，表示罗德参数L的影响越小；2)以L=-1 为例，图中以特殊符号标出了体胞失效临界点，临界应变值随着应力三轴度T的增加而减小。

2.2.2 低应力三轴度

对于低应力三轴度区(T＜0.5)，选取应力三轴度T范围为[-0.2，0.4]，变化间隔为0.1，罗德参数L范围为[-1.0，1.0]，变化间隔为0.25，共63 组不同的应力状态进行体胞模型分析。

以应力状态(T=0、L=0)为例，图9 显示了体胞模型随塑性应变发展εeq的演化过程。如图9 所示，空穴随着塑性应变发展而逐渐变小直至闭合，体胞失效机理为空穴闭合促使塑性剪切带形成[21]。

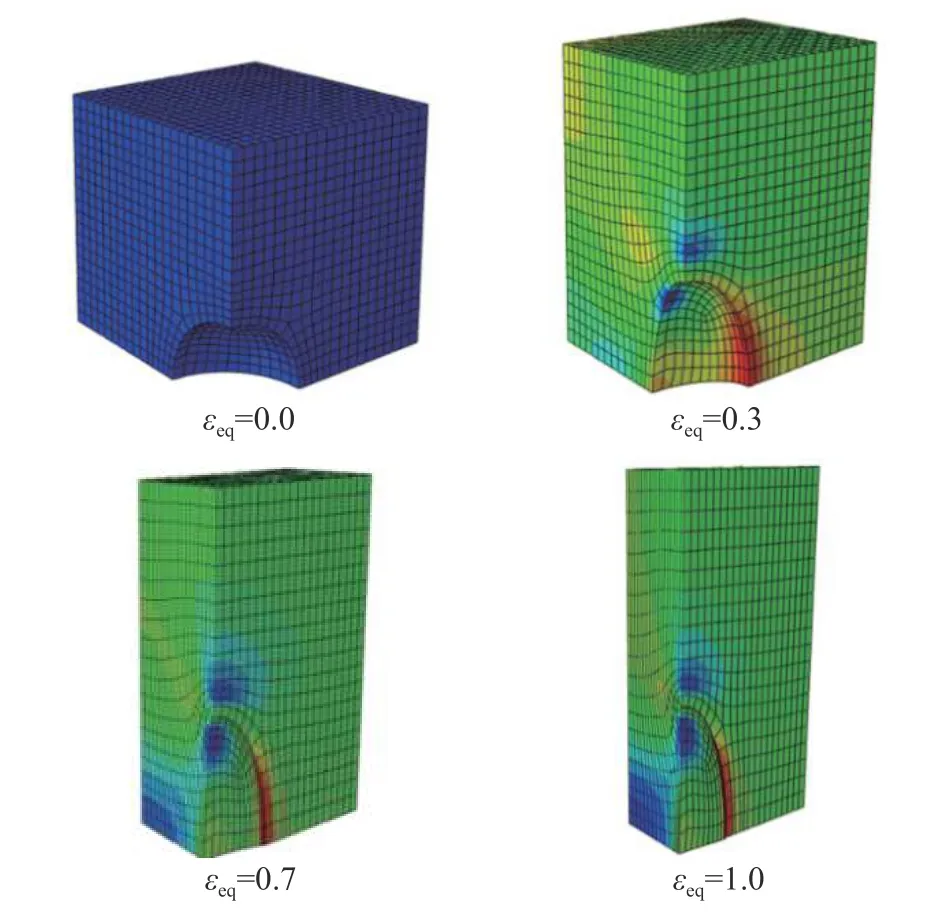
图 9 体胞模型随塑性应变发展演化过程(T=0、L=0)Fig. 9 Somatic cell model evolution process (T=0, L=0)

图 10 低应力三轴度空穴体积分数演化Fig. 10 Evolution of volume fraction of low stress triaxiality void

图10 给出了其中12 组有代表性的应力状态下的空穴体积分数演化曲线，图中空穴体积分数降为0 的点可看作空穴闭合临界点。从图中可以得出以下结论：1)应力三轴度T越高，空穴闭合的临界应变值越大，即临界应变值与应力三轴度T呈正相关；2)罗德参数值L越小，空穴闭合的临界应变值越大，即临界应变值与罗德参数呈负相关。

2.3 断裂准则推导

本文认为在微观尺度上体胞失效时刻对应宏观尺度上材料断裂起始时刻。因此，根据体胞分析结果得到体胞失效临界应变εcr与应力三轴度T和罗德参数L的关系式，再将其转化为宏观尺度上的材料断裂应变表达式即得到材料韧性断裂准则。

2.3.1 高应力三轴度

图11 显示了15 组不同应力状态下体胞失效的εcr-T数据点，在同一个应力三轴度T下，当罗德参数L分别为(-1，0，1)时，相同的应力三轴度T对应的临界应变值几乎重合。因此，在高应力三轴度下，罗德参数的影响很小，可近似忽略。

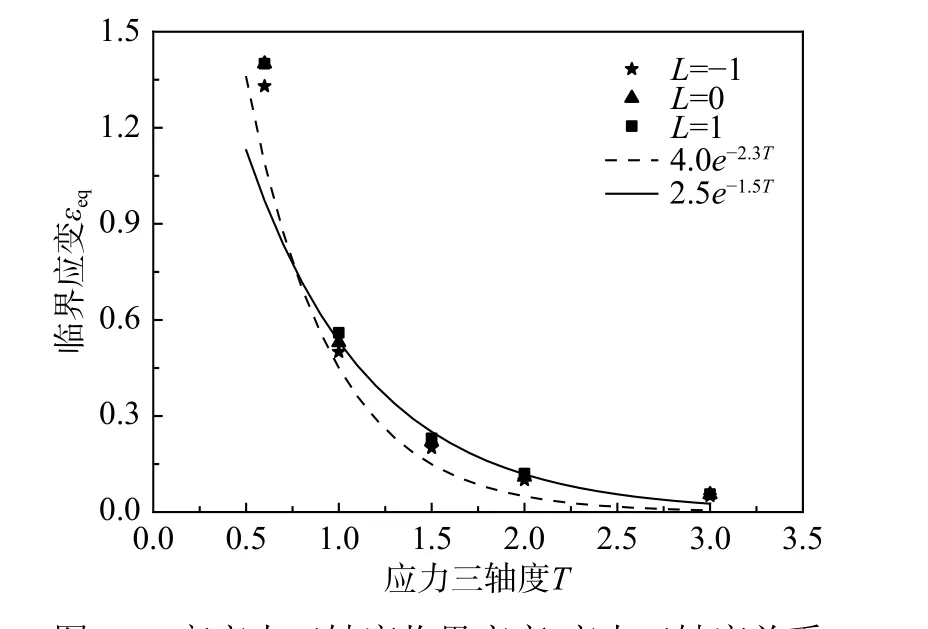
图 11 高应力三轴度临界应变-应力三轴度关系Fig. 11 The relationship of critical strain-stress triaxiality in high stress triaxiality area

2.3.2 低应力三轴度

1) 剪切断裂准则构建

基于低应力三轴度区体胞分析结果，本文参照Rice-Tracey 模型的幂指数形式，分别构造临界应变εcr与应力三轴度T的关系式以及临界应变εcr与罗德参数L的关系式：

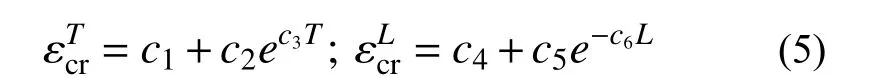
基于式(5)的形式，构造式(6)表示低应力三轴度体胞失效临界应变εcr与应力三轴度T和罗德参数L的相关性：

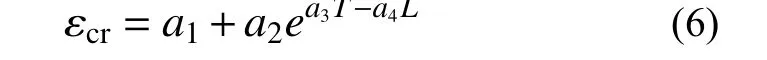
式中，a1、a2、a3、a4为自由参数。

图12 显示了63 组不同应力状态下体胞失效的εcr-T-L数据点，采用式(6)对图中的数据点进行拟合，得到a1=0.55，a2=0.51，a3=2.44，a4=1.43。

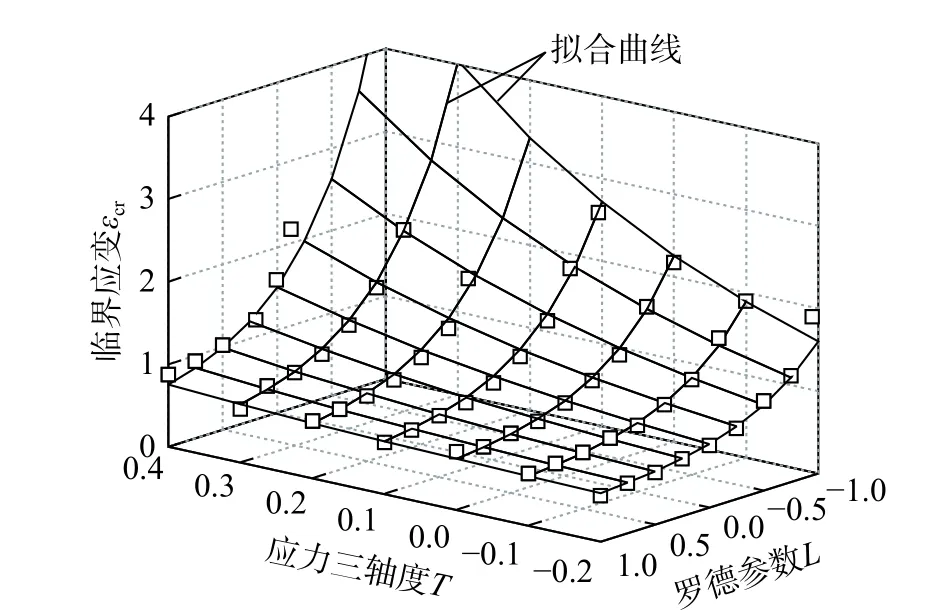
图 12 低应力三轴度临界应变-应力三轴度-罗德参数关系Fig. 12 The relationship of critical strain-stress triaxiality-Rod parameter in low stress triaxiality area

式中：εnc是导致空穴形核的等效塑性应变；εcr是导致空穴坍塌和局部剪切带形成的临界应变；p1、p2和εc是相应的系数；T为应力三轴度；n为幂强化系数。

由式(6)和式(7)得到空间应力状态下的剪切断裂应变计算公式(8)：

2) 剪切断裂公式简化

式(9)中含有4 个自由参数，校核工作量大，不利于工程实际应用。因此，根据现有的研究结果和数学方法[8,22-23]对式(9)进行简化，减少自由参数数量。

此外，应力三轴度T与罗德参数L有对应关系式(12)[8,22-23]，对L分别取T的一阶导数与二阶导数，并令T=0，有式(13)。

由式(13)、式(10)和式(11)有：

式(15)中参数(q3T-q4L)反映空穴演化的微观结构特征，其中罗德参数L的自由参数q4表示对空穴形状的影响程度。研究发现[22]，实际金属材料中空穴形状对材料性能的影响较小，可对自由参数q4进行简化处理。由于断裂应变对q4与幂强化参数n皆呈正相关[21]，故将q4近似地取为幂强化系数n。因此，式(15)可简化为式(16)：

综上所述，低应力三轴度区空间应力状态下的剪切断裂准则经简化后写成式(16)。

2.3.3 复杂应力状态

通过区分拉伸断裂模式和剪切断裂模式，联合式(4)和式(16)，以最低断裂应变作为极限断裂应变(εf)得到整体断裂准则，如式(17)。根据Bao 等[6]的研究结论，T≤-1/3 时钢材不会发生断裂，故本文断裂模型的极限断裂应变计算公式适用于T＞-1/3。

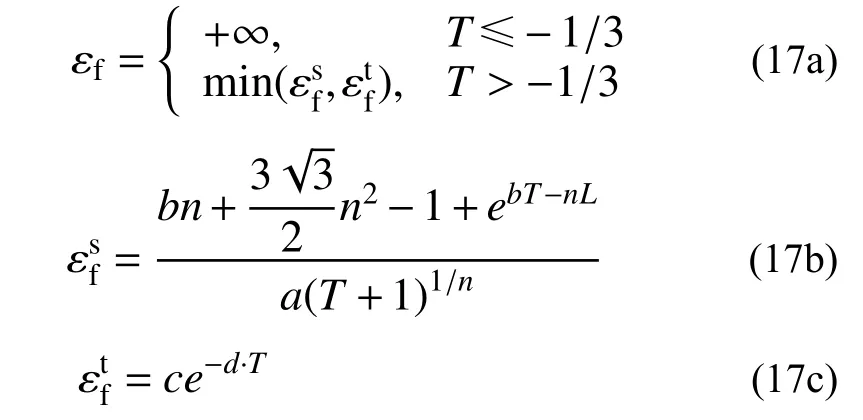
由于韧性断裂模型(式(17))描述的是材料在加载过程中应力状态基本保持不变时的断裂应变，故不能直接用于实际工程问题的计算。为定量描述材料损伤的累积过程，还需引入与塑性应变增量相关的损伤因子增量(ΔD)对韧性断裂模型进行调整，以考虑每个增量中的当前应力状态。

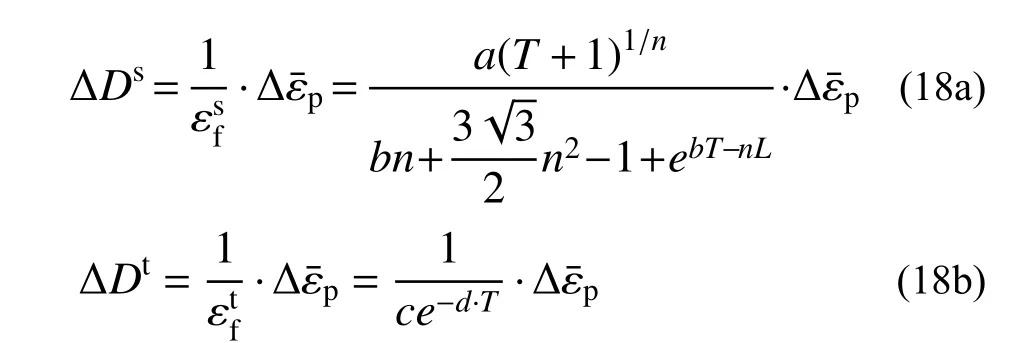
式中，ΔDs和ΔDt分别是由剪切荷载和拉伸载荷引起的损伤增量。

根据线性累计损伤理论[24]，累积每一加载步产生的损伤因子增量，定义总损伤因子D达到1 时材料产生破坏，故联合式(18)即可得到韧性断裂损伤模型：

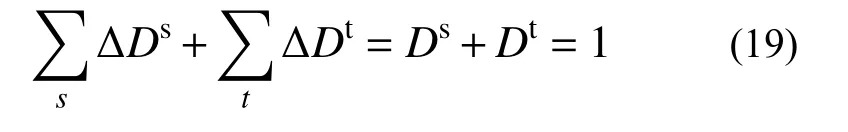
3 模型参数校核

本文基于文献[8, 22]完成的开槽圆棒试样NRB10、开槽平板试样GPS2 和剪切平板试样S0的单轴拉伸试验结果，通过ABAQUS 有限元模拟方法获得试件断裂起始位置的应力状态，在此基础对本文韧性断裂模型参数进行校核。

3.1 试验介绍[8,22]

NRB10 试 样、GPS2 试 样 及S0 试 样 均 由1200 mm 长、440 mm 宽和20 mm 厚的Q345 钢块切割而成，设计尺寸见图13。其中NRB10 试样和GPS2 试样为高应力三轴度区拉伸试件，S0 试样为低应力三轴度区剪切试样。试验采用MTS-810 材料试验系统，引伸计标距为50 mm，延伸率为30%。

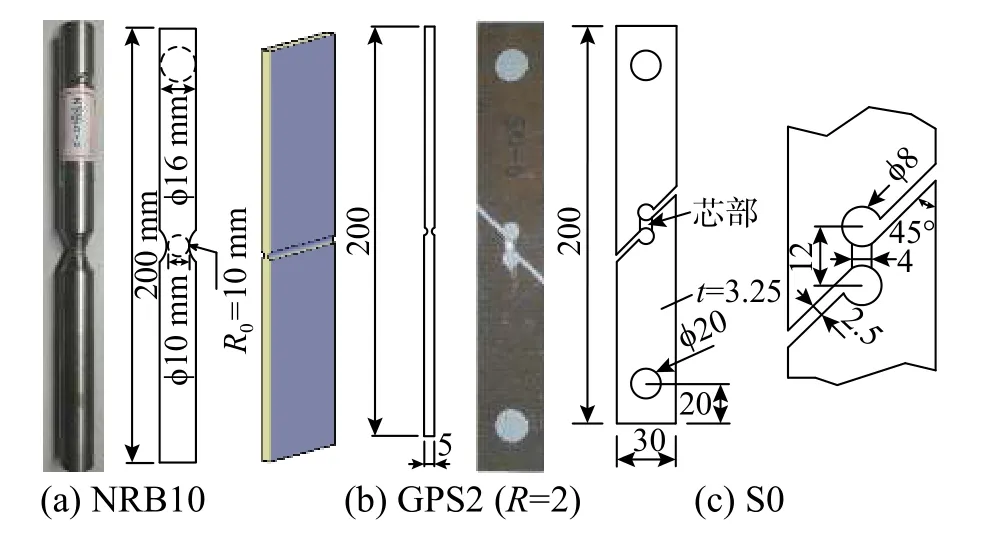
图 13 Q345 试样设计尺寸 /mmFig. 13 Q345 sample design size

3.2 数值模拟

对NRB10 试样、GPS2 试样及S0 试样分别进行数值模拟分析，以获得试样断裂起始位置的断裂应变和应力状态。在ABAQUS 软件中分别建立NRB10 试样轴对称有限元模型、GPS2 试样的1/8 模型、S0 试样沿厚度方向的1/2 模型，3 种试样的有限元模型及边界条件如图14 所示。根据文献[8]得到的超景深三维观测结果，Q345 钢材材料特征长度取为250 μm，因此对NRB10 试样、GPS2 试样有限元模型的槽口单元及S0 试样芯部单元分别进行加密，单元长度取为250 μm。

3.3 参数校核

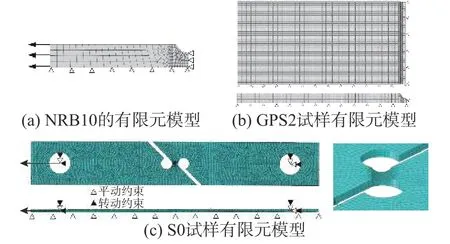
图 14 NRB10 试样、GPS2 试样及S0 试样有限元模型Fig. 14 Finite element model of NRB10, GPS2 and S0

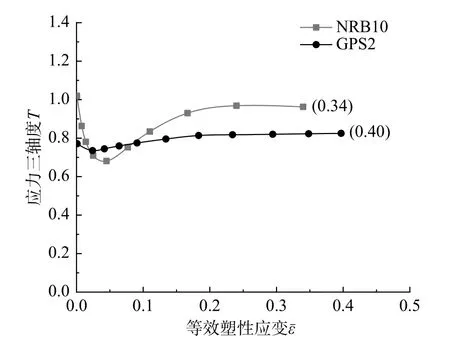
图 15 NRB10、GPS2 试验断裂起始位置应力状态Fig. 15 Stress state of NRB10 and GPS2 fracture start position

图 16 S0 试样断裂起始位置的应力状态Fig. 16 Stress state of S0 fracture start position

图15 显示了NRB10 试件和GPS2 试件断裂起始位置(槽口截面中心)的应力三轴度，图16 显示了S0 试样断裂起始位置(芯部外表面中心)的应力三轴度T和罗德参数L。如图15、图16 所示，断裂起始位置的应力状态在加载过程中不恒定，因此本文取平均应力三轴度Tav和平均罗德参数Lav表征断裂起始位置的等效应力状态[5-6]。平均应力三轴度Tav和平均罗德参数Lav分别根据式(20)和式(21)计算。

高应力三轴度下的NRB10 试样和GPS2 试样的平均应力三轴度Tav分别为0.85 和0.79，断裂应变分别为0.34 和0.40。低应力三轴度下的S0 试样平均应力三轴度Tav和平均罗德参数Lav分别为0.02 和-0.05，断裂应变为0.87。

将高应力三轴度下的两组Tav-εf对应关系{Tav=0.85，εf=0.34}和{Tav=0.79，εf=0.40}代 入 式(17c)，求解一组非线性代数方程，校核得到c=2.97、d=2.55。因此，断裂模型拉伸分支写成式(22)。

断裂模型剪切分支(式(17b))中含有2 个未知参数a、b，不能只由一组等效应力状态{T=0.02，L=-0.05，εf=0.87}直接校核。研究表明[22]，当应力三轴度高于1/3 时总会发生拉伸断裂，因此假设剪切断裂分支和拉伸断裂分支由轴对称拉伸应力状态(T=1/3，L=-1)作为分界。将T=1/3 代入式(22)得到另一组等效应力状态{T=1/3，L=-1，εf=1.265}。将这两组Tav-Lav-εf对应关系分别代入剪切断裂模型(式(17b))，其中幂强化系数n=0.22[8]，求解一组非线性代数方程，得到a=1.66、b=5.37。因此，断裂模型剪切分支写成式(23)。

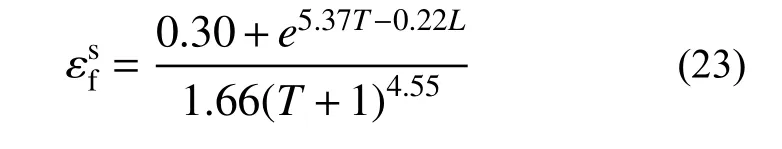
联合断裂模型拉伸分支和剪切分支参数校核结果，得到Q345 钢材在复杂应力状态下的断裂模型如式(24)。

4 断裂模型的应用与验证

本文提出的韧性断裂模型同时考虑了断裂中拉伸与剪切组合贡献，适用于拉-剪复杂应力状态下的钢节点断裂问题分析，为评估节点的安全性提供强有力工具。

4.1 试验介绍

本文采用十字型钢节点试件研究拉-剪复杂应力状态[25]，对模拟钢结构梁柱节点的断裂破坏行为具有一定的参考价值。本文设计了如图17 所示的Q345B 十字型钢节点试件(C12 试件)，其由16 mm厚的Q345B 钢板双面打磨至12 mm 后经线切割加工而成。

图 17 C12 试件尺寸 /mmFig. 17 Specimen size of C12 specimen

C12 试样中加工了一条初始间隙，该间隙用于模拟梁柱节点角焊缝焊接时未焊透而留下的间隙。间隙宽度为1 mm，长度为12 mm，间隙贯穿试件，共加工3 个相同试件。试验采用MTS Landmark 测试系统进行拉伸试验，通过引伸计测量50 mm 标距范围内的变形。

图18 显示了C12 试件的断裂破坏试验现象。如图18(a)，随着位移加载，试件初始间隙开始变宽，同时试件角部材料发生颈缩，在初始间隙上表面两角处开始产生裂纹；如图18(b)，裂纹产生后向两侧角部倾斜扩展，形成大约45°的倾角直至试样完全断裂。

图 18 C12 试件断裂破坏试验现象Fig. 18 Test phenomenon of C12 fracture and failure

4.2 断裂过程模拟及分析

采用ABAQUS 软件建立引伸计标距内的有限元模型，对初始缝隙两侧局部单元网格进行加密，缝隙附近加密区网格尺寸取0.25 mm，如图19 所示。

采用Fortran 语言编写断裂损伤模型(式(18)和式(19))的子程序，借助用户子程序USDFLD，将校核的断裂模型植入到ABAQUS 中。当单元的累积损伤D达到1 时，判断该单元失效，然后根据新的应力状态继续进行有限元计算，直到试样完全破坏。同时可根据单元的失效顺序预测裂纹的扩展方向。

图 19 C12 试件有限元模型Fig. 19 Finite element model of C12

将式(24)所示的断裂模型校核结果代入子程序对C12 试件在单调加载下的断裂破坏进行有限元计算分析，计算得到试样的荷载-位移曲线如图20 所示，可见有限元计算曲线与试验曲线吻合良好，同时还发现，C12 试件的试验曲线与模拟曲线的最后下降段曲线基本呈线性，因此将最后下降段的起点定义为断裂点[13,16]。

图 20 C12 试件的荷载-位移曲线Fig. 20 Load-displacement curve of C12

基于图20 得到的试样断裂荷载及断裂位移列于表1，表1 给出了试样断裂荷载及断裂位移模拟结果与试验结果的对比情况，可见预测误差均在15%之内，满足工程应用精度要求。因此，本文提出的韧性断裂模型具备良好的预测精度。

图21 显示了C12 试件数值模拟预测的裂缝扩展历程，C12 试件的断裂起始位置位于初始缝隙上表面两角，裂纹扩展路径与试验观测结果一致。因此，本文提出的韧性断裂模型能够准确捕捉十字型钢节点试件的断裂起始位置及裂缝扩展路径，并具有良好精度。

表 1 试验结果与断裂模型计算结果对比Table 1 Comparison of test results with fracture model calculation results

图 21 C12 试件模拟裂缝扩展历程Fig. 21 Crack propagation process of C12 specimen fracture simulation

图 23 C12 试件断裂起始位置罗德参数变化历程Fig. 23 Rod parameter at the fracture start position of C12

图22 和图23 分别显示了C12 试件断裂起始位置在加载过程中应力三轴度T和罗德参数L的变化历程。从图中可以看出，C12 试件断裂起始位置的应力三轴度T在加载过程中处于0.5～0.8 附近波动；罗德参数L在加载过程中处于0.1～0.9 附近波动，表明C12 试件在加载过程中缝隙两侧角部处于拉-剪复杂应力状态。因此，本文提出的同时考虑应力三轴度T和罗德参数L影响的韧性断裂模型，对预测结构钢材在复杂应力状态下的断裂行为具有良好工程应用前景。

5 结论

本文基于体胞模型空穴演化机理改进了现有的钢材韧性断裂模型，并校核了Q345 钢材断裂模型参数。以一组十字型钢节点试件为例，验证了改进后的韧性断裂模型用于预测钢节点断裂行为的适用性和准确性。主要结论如下：

(1) 本文采用体胞分析方法研究了钢材微观断裂机理，量化了空穴演化随应力三轴度及罗德参数的变化规律。体胞分析表明：① 应力状态对钢材韧性断裂性能的影响需要由应力三轴度T和罗德参数L这两个应力参数共同表征；② 在高应力三轴度区，空穴长大至失稳的临界应变值与应力三轴度T呈负相关，罗德参数L对临界应变值的影响很小，可近似忽略；在低应力三轴度区，空穴闭合形成塑性剪切带的临界应变值与应力三轴度T呈正相关，与罗德参数L呈负相关。

(2) 本文将体胞模型随应力三轴度T及罗德参数L的演化规律转化为宏观尺度上材料的整体材性，分别推导了高应力三轴度和低应力三轴度下断裂应变关于应力三轴度T和罗德参数L的表达式。与已有钢材韧性断裂模型相比，简化了断裂模型形式和参数校核过程。

(3) 对其他学者完成的3 组不同类型的Q345钢材材性试验进行有限元模拟分析，根据模拟得到的断裂起始位置的应力状态校核了Q345 钢材韧性断裂模型参数。

(4) 完成了一组Q345 钢十字型节点试件单轴拉伸试验，并用校准的断裂模型对其进行断裂预测分析，模拟预测误差小于15%且能准确捕捉钢材断裂起始位置及裂缝扩展路径，在拉-剪复合型应力状态下验证了本文的钢材韧性断裂模型的适用性和准确性。