输电塔线体系力学模型研究进展

陈 波，宋欣欣，吴镜泊

(1. 武汉理工大学道路桥梁与结构工程湖北省重点实验室，湖北，武汉 430070；2. 武汉理工大学土木工程与建筑学院，湖北，武汉 430070)

输电塔线体系是重要的电力能源基础设施，长期于野外恶劣环境下服役，容易发生损伤破坏，并造成严重的经济损失和次生灾害[1-6]。输电塔线体系的损伤破坏类型很多，在沿海地区频发强风引起的杆塔破坏倒塌事故[7-9]。近十年来，多个强台风“韦森特”、“天兔”、“黑格比”、“威马逊”、“彩虹”、“天鸽”等均给电网造成了很大破坏，很多服役多年的老旧输电线路发生了杆塔倒塌事故。在山地湿冷地区则多发覆冰灾害，引起大量输电线路覆冰倒塌。国内外多发输电线路的覆冰断线事故[10-13]。据不完全统计自20 世纪50 年代以来我国输电线路已发生冰灾事故上千次。2008 年我国南方遭受了严重的冰雪灾害天气，多个省份的电网遭受了严重的冰灾。国内外特别是我国西南地区发生过多起输电线路在地震作用下的灾害事故，造成了大量输电塔线体系的损伤破坏[14-17]。在沿海腐蚀性大气环境地区，则多发输电线路杆塔及金具的腐蚀损伤事故，也造成了严重损失。此外，国内外输电线路还发生过在下击暴流、龙卷风、高温断线等作用下的各类损伤破坏事故。由此可知，作为能源基础设施的输电塔线体系在服役过程中面临着各类自然荷载和环境效应的作用，多发灾变事故，造成了非常严重损失。因此，国内外均积极开展输电线路的监测评估与防灾减灾的研究和工程应用工作[3-4,18-19]。

输电线路的防灾减灾研究离不开输电塔线体系的力学模型。输电塔线体系是典型的高柔空间钢结构，具有刚度小、变形大、几何非线性效应显著等一系列特点。输电塔线体系与传统高耸结构相比既有相同特征也存在明显不同。相同之处是输电杆塔类似电视塔、通信塔等，具有高柔特征，低阶振型贡献占据了动力响应的绝大部分。显著不同之处是塔线体系中存在多跟输电线，而输电线从力学角度而言是具有小应变、大变形特征的悬索，具有非常显著的几何非线性效应。因此，输电塔线体系的力学模型和灾变分析方法非常复杂，国内外很多学者均开展了相应研究。输电塔线体系力模型的建立是开展输电线路监测评估和防灾减灾的基础和关键，它是综合了有限元、随机振动、变分理论、空气动力学、地震工程、计算机科学、结构分析理论和新材料科学等前沿科学的工程分析新技术，其研究工作还不有很多不足之处。本文在此就输电塔线体系力学模型研究现状和进展进行比较、论述与总结，在此基础上就输电塔线体系力学模型的发展进行展望。

1 输电线力学模型

输电线力学模型从早期的理论解析解阶段逐渐过渡到后来的非线性有限元阶段，经历了从简单到复杂，从宏观到微观的发展阶段[20-23]。早期以Irvine 为首的国外学者采用理论方法建立索的振动方程来描述输电线的性能[24-27]。随着杆系有限元和大变形理论的发展，输电线的模拟主要采用杆系有限元方法进行[4-5]，采用可拉不可压的杆单元模拟输电线，分别通过弹性刚度矩阵和应力刚度矩阵来考虑线性和非线性效应，这仍然是目前很多大型商业软件采用的方法。

由于当时计算机技术有限，进行大规模非线性有限元计算较为复杂和繁琐。因此，李宏男和白海峰[3]基于Hamilton 原理并采用等价线性化方法，通过建立等效的多质点模型来描述输电线的力学行为。21 世纪初以来，随着对输电线和悬索分析精度的要求，也伴随着计算机技术的迅速发展，大变形有限元计算方法和技术得到了迅速发展[28-29]。很多学者提出了各种类型的多节点索单元模型，通过将非线性刚度表述为初应力刚度矩阵和初位移刚度矩阵，显著提高了输电线及悬索的分析精度。但这些不同类型的高阶索单元往往缺乏显式表达式或根本无法进行显式表达，分析计算过程中需进行大量符号积分运算。因此，虽然计算精度很高，但计算量很大，耗时较长，效率较低。虽然计算桥梁单根斜拉索或悬索尚可以操作，但如果分析含有大量多分裂导地线的输电塔线体系时，由于计算模型规模宏大而效率低下，难以应用于实际工程。基于此，部分学者开展高精度索单元及其显式解的研究工作，并建立了几种多节点索单元的显式计算方法，结果表明这些方法在保证精度的前提下相比于符号积分算法可以极大提高计算效率。此外，输电线路的工程实际中往往需要掌握输电线股线的细部服役性能，因此部分学者也针对性地提出了分层股线模型、细观接触模型等描述股线性能的输电线模型。考虑到输电导线往往是采用多分裂形式使用，部分学者开展了分裂导线的研究工作，提出了典型分裂导线力学模型并开展了应用。以上这些力学模型方面的研究工作均对输电线的监测评估和防灾减灾研究提供了重要的支撑。

1.1 悬索理论分析模型

早期研究中，通常将输电线考虑为悬索进行其静动力性能的研究。Irvine 系统研究了悬索的振动特性，其研究结果常常作为理论解析解来衡量悬索的性能[24]。图1 显示了输电线分析模型，通过求解振动方程即可得到输电线的动力特性。对于输电线平面外振动而言，其频率ωv和振型 φv可表示为：

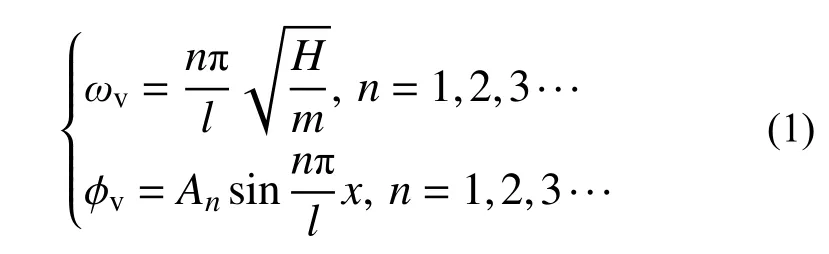
式中：H为输电线内力；l为输电线水平档距；m为输电线的线密度；x为输电线上某点距坐标原点的距离；An为振型系数。

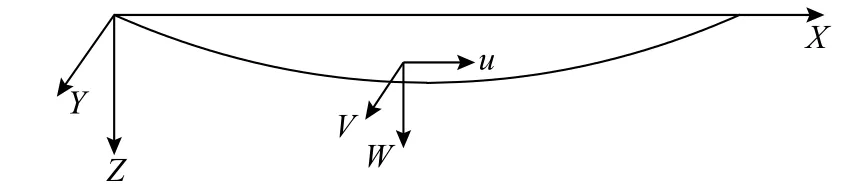
图 1 输电线分析模型Fig. 1 Model of a transmission line

式中：Bn为振型系数；h为输电线动张力增量；E为输电线弹性模量；g为重力加速度；A为输电线横截面积。上述超越方程一般可用图解法或数值方法求解。

1.2 杆系有限元分析模型

Irvine 所建立的悬索理论模型复杂，在理论解推导过程中引入了小弧垂假设。因此，对于实际悬索的分析计算存在一定的局限性。随着20 世纪计算机技术的应用，采用杆系有限元方法计算悬索得到迅速发展，因此输电线的计算方法也过渡到有限元方法。很多学者将输电线简化为多个只受拉不受压的杆系单元，陈政清等[30]基于虚功增量方程建立了空间杆系结构大挠度问题内力分析的UL 列示法。刘光栋和王解君[31]建立了空间杆系单元的几何非线性刚度矩阵的分解形式，基于最小势能原理得到了空间杆系单元的非线性几何刚度矩阵。基于杆系有限元模型，可将输电线刚度矩阵Kc表示为弹性刚度矩阵Ke和应力刚度矩阵Kσ之和：

式中：L为单元长度；H为输电线内力。输电线单元的质量矩阵则可采用集中质量矩阵或一致质量矩阵表达。将各单元质量矩阵和刚度矩阵组集，即可得输电线的的总质量矩阵和总刚度矩阵。

1.3 索单元分析模型

输电线的杆系有限元分析模型相较于Irvine 建立的悬索理论模型而言，考虑了应力刚度影响，具有明显进步。但是这种模型对于大弧垂、强非线性的大档距悬索而言，其分析精度有限，并且计算过程中非线性迭代收敛不易。造成这种现象的原因是杆系有限元理论对悬索的几何非线性性能的考虑不够精细。因此，基于索单元的输电线分析模型一直是研究的重点，很多学者提出了不同类型的索模型[32-45]。这些模型的基本思想是首先建立索单元应变ε 与形函数N、节点坐标Xe和节点位移Ue的关系。进一步地将输电线的刚度矩阵表示为基于索单元的弹性刚度矩阵Ke、初应力刚度矩阵Kσ和初位移刚度矩阵Kg之和：

式中：BL为线性几何矩阵；BN为非线性几何矩阵；L为单元长度；ξ 为单元等参变量；σ 为单元应力。输电线单元的质量矩阵仍然可采用集中质量矩阵或一致质量矩阵来表达。将各个单元的质量矩阵和刚度矩阵组集即得总质量矩阵和总刚度矩阵。

Peyrot 和Goulois[32]提出了一种分析任意形状输电线的迭代数值模型。他们采用索单元模拟输电线，并采用一个单独的子程序确定索单元的张力和切线刚度矩阵。对断线、不平衡覆冰荷载、风荷载作用下的结构进行了分析计算，考察了模型的有效性和收敛性。唐建民[33]建立了柔性结构非线性分析的杆单元有限元法。通过建立应变的非线性几何关系并考虑位移高阶量贡献，依据虚功原理建立了其力学模型。张其林[34]建立了连续长索非线性静动力分析的样条单元法。采用三阶B 样条基构建了索的等参元力学模型，该方法可以适用于松索、紧索及索系统的非线性静动力问题求解。唐建民等[35-36]基于悬索结构大变形特征，提出了一种基于欧拉描述的两节点索单元模型。进一步，他们提出了一种五节点等参数单元有限元模型。唐建民和沈祖炎[37]还提出了一种悬索结构非线性分析的滑移索单元法，建立了滑移单元非线性分析的力学模型。聂建国等[38]针对索长与悬索两节点之间的直线长度相近时迭代不易收敛的问题，提出了一种悬链线索单元的改进算法。杨孟刚和陈政清[39]基于抛物线假定建立了一种两节点悬链线索元非线性力学模型，同时推导了索端张力的精确表达式。武建华和苏文章[40]建立了一种四节点等参曲线索单元有限元模型，结果表明该模型具有精度高、收敛快的特点。胡建华和王连华[41]提出了一种索结构几何非线性分析的悬链线索单元模型，建立了单元刚度矩阵和单元等效节点荷载。张立新和沈祖炎[42]总结了不同索单元有限元模型的优缺点，指出了悬链线单元在精确分析索自重影响时的优点。研究表明：悬链线单元模型具有高精度、高效率的特点，同时适用于小垂度索和大垂度索。任伟新等[43-44]提出了一种新的两节点抛物线索单元。该单元静刚度矩阵表达式由动刚度矩阵的解析表达式对频率取零极限得到，具有较高的分析精度。通过数值算例和模型试验验证了该单元的准确性和高效性。Thai和Kim[45]提出了一种索结构的非线性悬链线索单元并推导了单元刚度矩阵和节点力表达式，通过结合增量迭代算法和Newmark 直接积分法实现了非线性方程的求解。

1.4 多质点分析模型

基于索单元的输电线计算方法虽然精度高，但是计算过程中需要进行数值积分，因此计算量大，较为耗时。为简化计算，李宏男等学者[46-47]考虑将输电线进行等价线性化处理而形成多质点模型。其基本思路是在平面内将输电线考虑为弹性质量-连杆体系，利用Hamilton 原理建立输电线的势能和动能表达式，并进一步对广义坐标求解而建立输电线的质量矩阵与刚度矩阵。在平面外通过将输电线简化为垂链模型建立其质量矩阵和刚度矩阵。

如图2 所示的输电线平面内简化为7 连杆体系。设各连杆的长度和转角分别为li和θi，则输电线单元转角和长度的广义坐标ξ 和δ 可表示为：

式中：mi和di分别为第i个质点的质量和距离坐标轴的竖向距离；xi和yi分别为第i个质点沿水平和竖向的位移；Ug和Ue分别为输电线的重力势能和弹性势能。

基于Hamilton 原理可建立输电线动能Tline、势能Uline和虚功Wline的能量关系[48]：

式中，t1和t2分别为非保守力做功的时间区间。

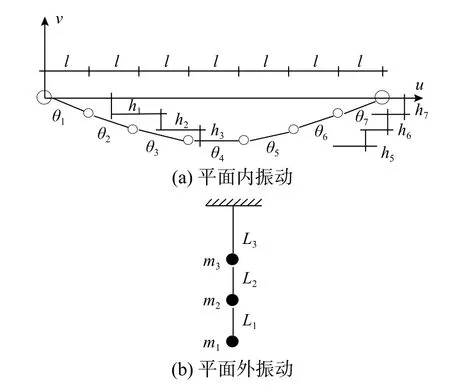
图 2 输电线的多质点模型Fig. 2 Multi-degree of freedom (MDOF) model of a transmission line

采用广义坐标表示输电线的动能、势能和虚功，就可以从Hamilton 原理表示的动力学变分形式推导得到输电线的运动方程。将输电线的动能用广义坐标和它们的一次导数表示，势能用广义坐标表示。非保守力在广义坐标的一组任意变分所引起的虚位移上所做的虚功可以表示为这些变分的线性函数，并将其代入Hamilton 方程可得输电线振动的Lagrange 方程[49-50]：

1.5 显式索单元模型

索单元具有分析分析精度高、适用面广、适用性好等一系列优点，但由于系统矩阵计算中需要复杂的积分运算，因此数值计算量非常大、计算效率较为低下，导致其在实际应用中受到很多限制。基于杆单元的计算方法计算速度快，但由于采用杆件模拟悬索而导致计算精度有限，特别是对大垂度输电线计算精度不理想。多质点分析模型基于Hamilton 原理和Lagrange 方程将输电线的几何非线性行为进行等价线性化，可以离线形成输电线质量矩阵和刚度矩阵，动力计算较为简洁快速，但精度有限，特别是无法计算输电线的内力响应，是其一个明显缺陷。基于悬索结构模型的缺点，很多学者开展了显式索单元的研究工作。Jayaraman 和Knudson[51]较早尝试建立了一种悬链线索单元模型。该模型具有显式刚度矩阵，具有计算精度高且运算量小的特点。袁行飞和董石麟[52]提出了一种二节点曲线非线性索单元模型。该单元克服了广泛使用的二节点杆单元精度低和多节点索单元模型复杂的缺点。基于拉格朗日坐标描述法和卡氏第一定理推导了索单元刚度矩阵的显式表达式，在保证分析精度的前提下有效地提高了分析效率。王春江等[53]提出一种考虑初始垂度影响的非线性索单元模型。运用虚功原理推导了考虑初始垂度影响的两节点非线性索单元表达式，并建立了索单元的单刚矩阵的显式表达式。通过建立该非线性索单元的修正项，给出了垂度影响因子的变化曲线。该非线性索单元兼顾了多节点索单元高精度的优点，同时具有节点少、求解效率高的优点。杨孟刚和陈政清[54]建立了一种两节点悬链线索元非线性模型。他们基于UL 列式的虚功增量方程和索的悬链线方程，并对索的自重影响未作任何的近似，推导建立了显式的索单元切线刚度阵。袁驷等[55]根据悬索结构的精确解析解，针对索结构找形构造了线性和非线性两大类共5 种单元。构造了与张力、荷载、悬挂点的坐标相关的精确索单元，推导建立了单元刚度矩阵的显式表达式。计算结果表明该单元具有精度高、收敛速度快的优点。多节点索单元自由度过多，分析计算效率低下。相较之下，三节点索单元自由度较少，同时三节点索单元计算精度与其他高阶索单元相比并不逊色。基于此，陈波等[56]建立了三节点显式索单元力学模型并将其应用于输电线的响应分析，结果表明这种显式索单元具有精度高、收敛快的特点。他们还建立了一种两节点曲线显式索单元模型[57]，该模型在非线性刚度矩阵中包含了显式初应力刚度矩阵和显式初位移刚度矩阵。输电线的非线性刚度矩阵Kc可表示为弹性刚度矩阵Ke和初应力刚度矩阵Kσ和初位移刚度矩阵Kg之和，其中初位移刚度矩阵Kg为：

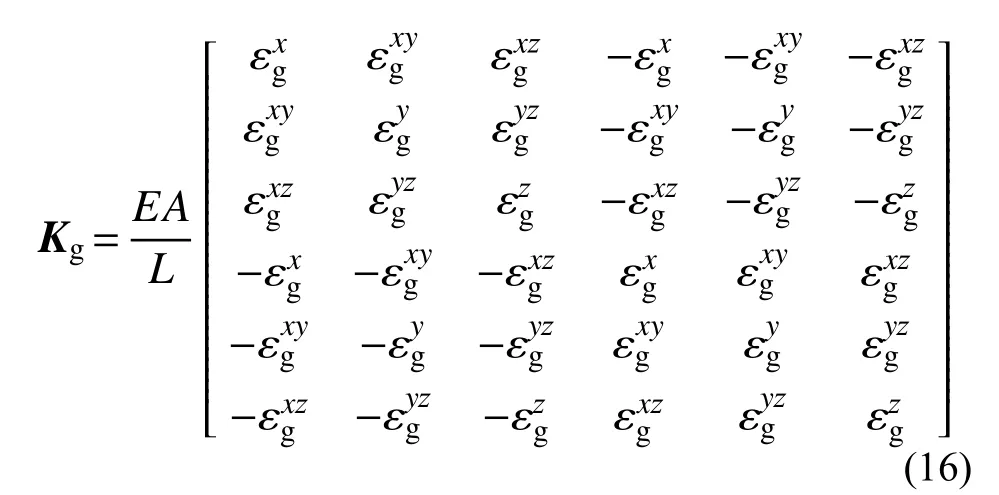
1.6 扭转索单元模型

输电线在服役过程中，由于覆冰作用将改变其外形，形成不规则截面(如图3 所示)。因此，输电线容易表现出扭转特性。以往部分学者基于杆系有限元方法建立了可以考虑扭转效应的杆单元模型来模拟输电线。但如前所述，杆单元模拟输电线存在一定误差，精度有限。而考虑覆冰扭转效应的索单元还较为欠缺。Nigol 等学者[58-60]开展了覆冰输电线驰振的研究。通过实验提出了输电线扭转刚度的计算公式，该公式可以考虑张力、档距、张力单导线扭转刚度的影响。但该模型只适用于小档距输电线，而对于大档距输电线误差较大。Wang 和Lilien[61]建立了一种改进的输电线扭转刚度公式，但该方法计算过程复杂。朱宽军和刘彬[62]研究了覆冰厚度对架空输电线路扭转刚度的影响，但忽略了覆冰的偏心影响。李嘉祥等[63]开展了覆冰分裂导线扭转刚度的研究。提出了一种考虑偏心的导线扭转刚度计算方法，并进一步研究了覆冰对输电线扭转刚度的影响。冯珂等[64-65]提出了一种输电线三节点扭转索单元模型。图4 给出了输电线三节点扭转索单元坐标系定义，该单元单个节点上具有四个自由度，包括三个平动自由度和一个扭转自由度。扭转索单元的刚度矩阵KN可表示为：

式中：KcS为应力刚度矩阵；KcL为弹性刚度矩阵；KcN为初位移刚度矩阵；Kice为偏心刚度矩阵；BcL为线性几何矩阵；BcN为非线性几何矩阵；Ncq为偏心刚度矩阵形函数；D为弹性矩阵；S代表输电线关于Z轴的静距；L为单元长度。

1.7 分层股线模型

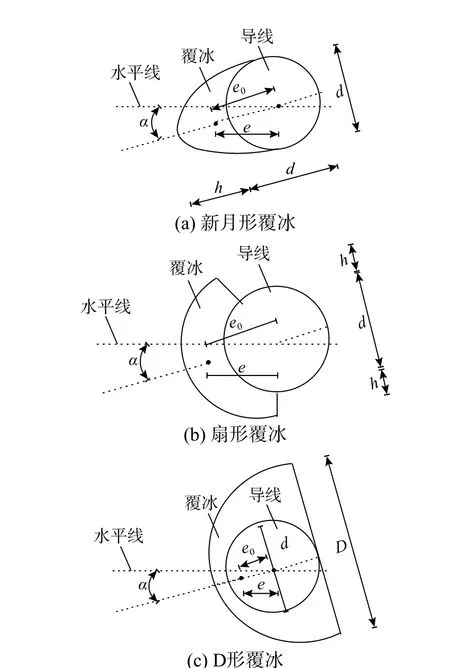
图 3 输电线不规则覆冰形状Fig. 3 Irregular ice shapes of a transmission line

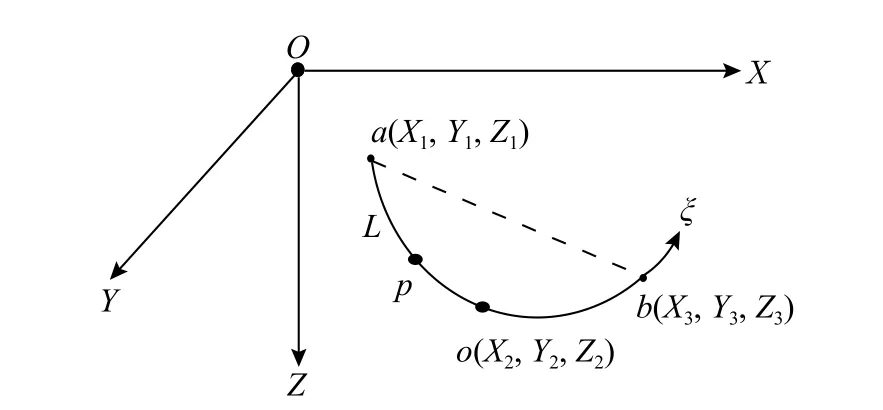
图 4 扭转索单元坐标系定义Fig. 4 Coordinate definition of torsional cable element

输电线实际上是由多根股线缠绕形成，而对于地线往往采用钢芯铝绞线构成。输电线各股缠绕复杂。在外荷载和温度等作用下，内部各股线表现出不同的力学性能[66-67]。如在输电线送电引起的高温作用下，容易发生内部钢芯受力减小而外层铝股承受主要张力的情况，从而导致输电线发生受力不均而断裂。因此，建立输电线的分层股线模型并研究输电线各层股线的受力特点具有重要的实际意义。陈波和龚小芬[68-69]提出了一种输电线的分层股线模型，该模型考虑了不同层股线间的挤压效应和泊松效应。通过建立各层股线承受的挤压力和股线纵向协调方程，求解各股线的内力。该模型实现了输电线分析从单根线层面向股线层面的改进。进一步地，邓静伟等[70]基于该分层股线模型研究了外层腐蚀对架空地线各层股线承载力的影响。

图5 给出了输电线各层股线的受力图，输电线受拉将导致各层股线产生轴向伸长和相邻层挤压。第i层股线沿导线轴向的应变Hi由两部分产生：一部分是由张力fi产生的轴向变形Hif；另一部分是由于泊松效应，层间挤压力pi产生的变形Hip。由弹性力学原理可得第i层股线的沿纵向的变形：

当输电线层数较多时将会产生正压力累加，则第i层股线承受的挤压力pi等于其外层股线各股层层间挤压力之和：

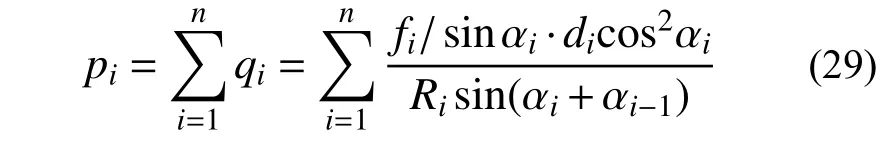
式中：Ri为第i层股线所在节圆半径；qi为第i层股线的正压力；di为第i层股线直径；fi为第i层单股线纵向张拉力；αi为第i层股线的螺旋升角；Ti=fi/sin αi为第i层单股线沿自身轴线方向的张拉力。

输电线第i层股线的横向变形ΔR由泊松效应产生的径向收缩Δr1和层间挤压力产生的径向压缩Δr2两部分组成。不考虑螺旋升角的变化则第i层股线纵向变形满足变形协调方程，由此推导可得：

式中：Ai为第i层截面积；Ei为第i层弹性模量。

图 5 输电线股线受力图Fig. 5 Forces of a transmission line

输电线各层股线承受的纵向力之和等于导线整体所受的张拉力：

式中：ni为第i层股线的根数；f为输电线承受的张力。通过求解式(31)即得各层股线内力。

1.8 细观接触模型

输电线的分层股线模型相比于整体输电线的模型而言，具有明显进步，它实现了股线层级的内力分析评定。在输电线的实际服役过程中，恶劣自然环境如腐蚀、覆冰、老化等容易引起股线的破坏，从而在股线表面造成损伤。即使是分层股线模型也无法详细描述输电线的细部受力特征，特别是无法有效掌握各股线之间的非线性接触效应。因此，有必要开展股线的细部承载力研究，这就需要建立输电线精细化的细观接触模型。基于此，吴永祥[71]提出了一种输电线的细观接触模型。该模型对于各根股线采用具有接触功能的实体单元建立，同时该模型可以反映股线的泊松效应和各根股线之间的挤压和接触滑移效应。该模型分析精度很高，可以考虑股线的细部损伤对整体输电线承载力的影响。

式中：B为股线单元几何矩阵；D为股线单元弹性系数矩阵；N为股线单元形函数矩阵；Ω 为股线单元积分区域。bs为作用于股线单元的荷载体积力向量；ps为作用于股线单元的外荷载分布力向量；A为股线单元外荷载作用面积分区域。

图 6 输电线细观接触模型示意图Fig. 6 Micro-contact model of a transmission line

各层股线在外荷载作用下将发生接触挤压作用，在股线之间形成接触面和接触应力。如图7所示，股线连接处分为接触面和目标面。接触面上的节点M与目标面发生接触，接触距离d必须大于或者等于零，这称为接触协调条件。如果接触距离小于零，则表示两个接触面之间发生了相互穿透，违反了接触协调条件。各股线之间的接触效应分析可采用罚函数法，接触力fn可表示为：

式中：Kn为各股线之间的接触刚度；d为股线接触面积之间的距离。

由于每根股线均可建立受力平衡方程，因此整个输电线的受力平衡方程实际上是一系列方程。输电线各股线之间的相互作用是一个非常复杂的非线性接触过程，因此其非线性接触效应的分析必须经过多次迭代方能完成。必须所有的股线都满足接触迭代收敛条件，则整个输电线的分析才能完成。进一步地，陈波和邓静伟[72]基于输电线的细观接触模型提出了一种架空输电地线股线接触效应分析方法及系统。此外，利用该模型张宇等[73]研究了股线挤压效应对架空地线受力性能的影响。

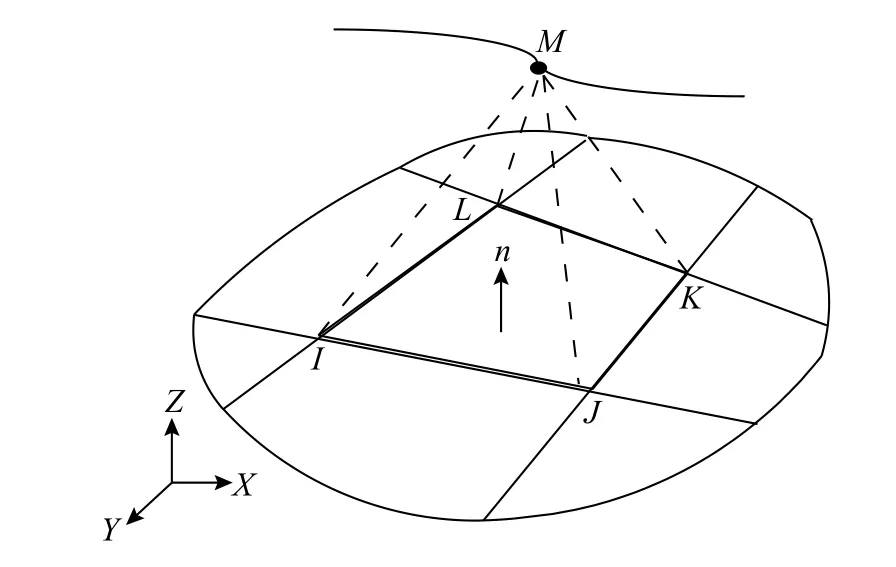
图 7 股线细部接触示意图Fig. 7 Deformation of a transmission line in radial direction

1.9 分裂导线模型

分裂导线由多根输电线及其中的间隔棒所组成[74-76]。间隔棒通常采用梁单元进行模拟。而现有研究中输电线可采用杆单元或索单元进行模拟，其刚度矩阵KSC为：

式中：nc为分裂导线的数量；nb为间隔棒数量；KC为单根导线刚度矩阵；KBR为间隔棒刚度矩阵。

围绕输电分裂导线的力学模型和响应，国内外学者也开展了系统研究。何锃等[77-78]建立了分裂导线扭转舞动的动力学模型。他们还建立了一种新单元的分裂导线力学模型。该模型假设输电线与间隔棒刚性连接，通过忽略位移导数的高阶项影响推导建立了分裂导线的单元刚度矩阵。进一步地，何锃和赵高煜[79]提出了分裂导线的新型三维有限元模型，推导建立了单元质量和刚度矩阵，实现了带防振锤分裂导线自由振动分析。刘小会等[80]利用一种三节点等参单元模型进行了分裂导线舞动非线性有限元分析。该模型中节点具有三个平动和一个扭转共计四个自由度，用欧拉梁单元离散间隔棒，利用虚功原理建立了覆冰分裂导线非线性振动方程。

晏致涛等[81]建立了一种基于结点六自由度的四分裂分裂导线力学模型。参数分析表明：弧垂、分裂间距、边界条件等对抗扭刚度均有较大的影响，间隔棒的数量不能显著提高输电线抗扭刚度。沈国辉和徐亮[82]建立了分裂导线的覆冰跌落模型，利用该模型研究了分裂导线与合成单导线的覆冰脱落的差异。通过参数研究考察了分裂导线和间隔棒数量对脱冰响应的影响。谢增和刘吉轩[83]提出了一种架空输电线路分裂导线扭转刚度计算新模型和方法。首先推导了子导线扭转时的实际张力公式，考虑输电线和两端高度差建立了分裂导线扭转刚度的力学模型和计算公式，该模型可以清晰地描述各种参数对分裂导线扭转刚度的影响。谢增和刘吉轩[84]还利用Hamilton 变分原理提出了一种改进的覆冰分裂导线舞动模型。通过引入一种新的分裂导线扭转刚度计算方法，建立了分裂导线固有频率公式和改进的覆冰分裂导线舞动分析模型。傅观君和王黎明[85]通过对分裂导线的扭转能量增量的分析，建立了分裂导线扭转刚度模型。进一步地通过真型分裂导线扭转试验验证了力学模型的准确性并开展了舞动机理研究。蔡君艳和刘习军[86]建立了带刚性间隔棒的覆冰四分裂导线耦合振动模型，基于该模型建立了覆冰四分裂导线舞动近似解析解。胡琴和于洪杰[87]基于力矩平衡关系，建立了以悬挂绝缘子轴向拉力、倾角为输入参量的分裂导线覆冰扭转力学模型。利用该模型开展了分裂导线等值覆冰厚度计算并在雪峰山试验基地开展了耐张塔3 分裂导线覆冰实测研究。刘小会等[88]建立了四分裂导线翻转的力学模型。他们从分裂导线的大角度转动出发，提出了新的输电线路翻转模型，该模型可以描述影响分裂导线翻转的各种因素。张志强等[89]建立了一种两分裂导线风致响应的等效分析模型及方法，便于工程应用上快速开展分裂导线风致响应计算。总体而言，虽然国内外开展了一些分裂导线的研究工作，但主要工作集中于分裂导线的静动力响应分析，对于分裂导线力学模型的研究还不完善，还有很多工作值得开展。

1.10 基于扭转索单元的分裂导线显式模型

为了提高分裂导线的分析精度，冯珂等[64-65]采用高精度的扭转索单元来构建分裂导线力学模型，同时通过建立质量矩阵和刚度矩阵的显式表示可以有效提高分析效率。分裂导线在服役过程中容易发生大变形和大转角。因此，分裂导线中的间隔棒通常采用考虑大转动的空间梁单元模拟。在建立分裂导线模型时，子导线采用每节点4 个自由度的悬索结构。通过对间隔棒空间梁单元模型进行自由度缩减使得两者可以有效组合。引入自由度缩减矩阵对间隔棒梁单元进行自由度缩减处理，可得缩聚后的间隔棒刚度矩阵KBR。基于扭转索单元的分裂导线显式模型的刚度矩阵KN可表示为：

2 输电塔力学模型

2.1 梁系有限元分析模型

梁系有限元模型可以考虑输电杆塔中各种主材、斜材、横隔材和辅助材的作用，因此可以准确地反映输电杆塔的静动力性能，并且便于商业有限元软件操作，受到了广泛的应用。在实际应用中可以根据分析精度的要求选择不同类型的梁单元。如在商业有限元软件中，模拟输电杆塔的杆件可以采用欧拉-伯努利梁单元，可以采用考虑剪切变形的铁木辛柯梁单元，还可以采用考虑截面翘曲自由度的梁单元等。

2.2 杆系有限元分析模型

基于梁单元的输电杆塔模型具有很好的分析精度，适用于各类静动力响应分析计算。但是对于普通工程设计人员而言，商业有限元软件操作过于复杂，同时杆塔结构设计过程中并不需要非常精细的有限元分析。因此，输电杆塔商业设计软件往往基于杆系有限元模型来分析输电杆塔的承载力状况。输电杆塔中的一些辅助材如果采用杆单元建模，则将导致杆塔部分位置变成可变体系，导致无法计算。因此，杆系模型中往往将辅助材等一些杆件简化，只保留主材、斜材、横隔材等主要受力构件。其计算结果为杆件的轴向应力，忽略了杆端的弯矩作用。

2.3 串联多自由度分析模型

输电杆塔杆件众多，空间三维有限元模型可以精确描述结构受力特征。但输电塔三维精确力学模型计算量很大，对于结构振动进行详细参数研究较为困难。此外这种精确三维力学模型的风荷载、地震作用和其他动力荷载样本也几乎不可能精确获得。因此，很多学者对输电杆塔结构采用二维串联多自由度模型以满足动力分析和参数研究的需要[93-95]。首先建立输电杆塔的精确三维有限元模型，形成其整体质量矩阵Mt和刚度矩阵Kt。进一步地基于三维模型确定结构主要的水平构件和附加质量较为集中的位置，可将这些位置设置为结构的节点层。在串联多自由度模型的建立过程中可抓住主要矛盾，略去次要因素，采用模型降阶的办法。首先将输电塔的结构构件和非结构构件的质量集中于所选择的n个节点层。节点层主要选择存在较多主要构件的平台之处。图8显示了输电塔典型的串联多自由度模型。

1) 对输电塔第j节点层中各节点施加总和为1 的水平力(j=1,2,···,n)。设第j节点层共有Nj个节点，求解静力平衡方程：

式中：f为荷载向量，该向量中除对应于第j节点层Nj个节点受力方向的元素值为1/Nj外，其余均为0；x为位移。

2) 确定第j节点层中各节点的平均水平位移。从位移向量x中选取第j楼层Nj个节点的位移值xm(m=1,2,···,Nj)并取平均值即得柔度系数δji(i,j=1,2,···,n)：

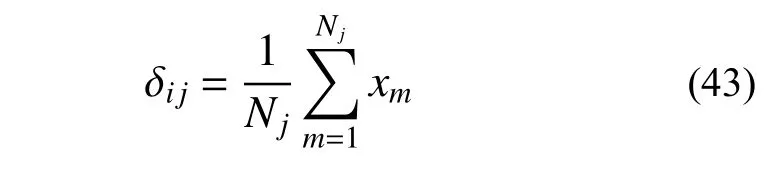
3) 重复以上操作可确定所有柔度系数并形成柔度矩阵Φ，求逆即可得输电塔的串联多自由度模型的刚度矩阵KD=Φ-1。

4) 模型的质量矩阵可采用集中质量矩阵：

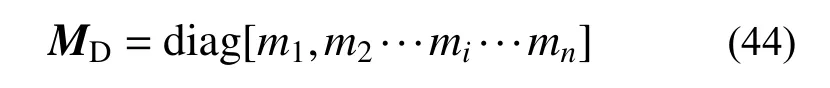
式中，mi为第i节点层的集中质量。

3 输电塔线体系力学模型

3.1 杆系有限元模型

基于不同类型的输电线模型和输电塔模型，即可构建不同的输电塔线体系力学模型。目前较多采用的是基于商业有限元软件如ANSYS、ABAQUS等构建的输电塔线体系模型。这些模型均采用杆单元模拟输电线，输电线刚度矩阵Kc可表示为单元弹性刚度矩阵Ke和应力刚度矩阵Kσ之和。输电线的质量矩阵可采用集中质量矩阵表示。采用空间梁单元建立输电塔模型。组集各输电塔和输电线的贡献即可形成输电塔线体系的力学模型：矩阵；nt和nl分别为塔线体系中杆塔和输电线的数量。

图 8 串联多自由度动力分析模型Fig. 8 Dynamic analytical model with lumped masses

输电塔线体系杆系力学模型可采用商业有限元软件建立，具有建模简单快捷的优点，便于开展塔线体系的各类风振地震、断线覆冰等静动力响应分析[96-102]。但这种力学模型在描述输电线非线性反应方面的精度稍显不足。此外，商业有限元软件的减振阻尼器模型非常有限，在输电线路的减振控制和参数研究方面具有明显不足。

3.2 索系有限元模型

针对杆系有限元模拟输电线精度有限的问题，有学者提出了输电塔线体系的索系有限元模型[103]。在该模型中，输电杆塔仍然采用梁单元建立三维空间有限元模型，而输电线则采用索单元建立。这样可以克服采用杆单元模拟输电线造成的非线性大变形响应精度有限的问题。输电线的刚度矩阵Kc可表示为弹性刚度矩阵Ke和初应力刚度矩阵Kσ和初位移刚度矩阵Kg之和。塔线体系的总刚度矩阵K为：

输电塔线体系的索系模型与杆系模型相比提高了整体分析精度，特别是对输电线的分析精度明显提高。但这种模型建模较为繁琐，目前只能依据编程实现分析，无法采用现有商业有限元软件操作，这给这种模型的应用带来了不便。

3.3 多质点动力等效模型

另外一种较为典型的输电塔线体系分析模型即为李宏男等[46-47]率先提出的输电塔线体系多质点力学模型（如图9 所示）。其基本思想与输电线的多质点模型类似，将输电塔线体系的动能T表示为广义坐标及其一阶导数，塔线体系的势能U单独用广义坐标表示。塔线体系非保守力在广义坐标的一组任意变分所引起的虚位以上所做的虚功可以表示为变分的线性函数：

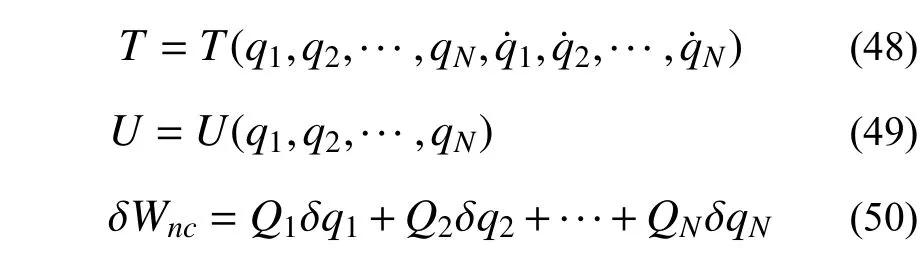
式中：Q1,Q2,···,QN为广义力函数。

对于塔线体系平面内和平面外振动可分别等效为悬索和垂链。一个包含多塔多线的输电塔线体系如图9 所示，体系的动能T和势能U可表示为：

将输电塔线体系式动能和势能的表达式代入拉格朗日方程，求解 ∂T/∂ξ˙i和 ∂T/∂δ˙i可得塔线体系的质量矩阵，求解 ∂U/∂ξi和 ∂U/∂δi可得塔线体系的刚度矩阵。输电线路由多个输电塔和多条输电线所组成，实际分析中通常选取有限数量的塔线即可反映系统的动力性能[104]。以一塔两线模型为例，塔线体系平面内振动的刚度矩阵Ki和质量矩阵Mi为：

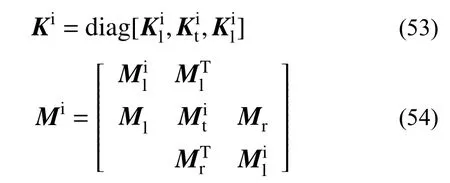
图 9 输电塔线体系多质点模型Fig. 9 MDOF model of a transmission tower-line system

3.4 索塔动力分析模型

输电塔线体系的杆系有限元模型、索系有限元模型和多质点模型各有优缺点。杆系有限元模型建模方便，便于采用商业软件操作，但是对输电线的分析模拟精度有限，并且计算工作量大，对于振动控制研究和参数分析略显不便。索系有限元模型虽然能够精确地分析输电线的静动力响应，但存在建模复杂、运算量大等问题，实际应用较为繁琐。多质点模型采用基于能量法则的非线性等效方法，运算速度快，便于进行振动控制分析和参数研究，但是对输电线的计算精度也较为有限。基于此，部分学者开始了索塔动力模型的研究工作。杨必峰和马人乐[105]建立了一种输电塔线体系的索杆混合模型。他们采用预拉力的直线单元模拟输电线，采用零应力的直线单元模拟输电塔，这种模型使输电线和杆塔的单元刚度方程形式得到了统一，便于分析计算。陈波和陈家鑫[106]结合不同模型的优点，提出了一种输电塔线体系的新型索塔力学模型。该模型的基本思想是对于输电杆塔采用串联多自由度动力分析模型，而对于输电线则采用索系有限元模型。同时在模型中还考虑了杆塔扭转刚度和输电线扭转刚度的影响。因此，输电线的分析计算依然采用非线性有限元方法，输电线的刚度矩阵Kc为弹性刚度矩阵Ke和初应力刚度矩阵Kσ和初位移刚度矩阵Kg之和。塔线体系的总刚度矩阵K和总质量矩阵M为：

采用这种模型优点非常明显，通过输电杆塔进行缩聚形成了串联多自由度动力分析模型，极大地减小了输电杆塔的动力自由度，便于进行动力响应分析和减振控制研究。考虑到塔线体系中的大变形大转角等非线性效应主要来自于输电线，通过采用显式索单元方法模拟输电线，可以准确有效地把握输电线的非线性效应，同时有效考虑了输电线和杆塔之间的动力耦合效应。由于该模型可以有效地描述塔线体系的动力偶联效应、输电线的强非线性效应，同时有效地兼顾了分析及效率和精度，大规模的多塔多线输电线路动力响应分析、减振控制分析和系统的参数研究可以有效地开展。基于这种模型，他们开展了输电塔线体系地震响应的研究和减振控制分析，取得了良好的效果[107]。

4 输电塔线体系力学模型的应用

相对于塔线体系力学模型的研究工作而言，基于塔线体系模型开展的强风强震、覆冰、断线以及减振控制方面的研究工作则较多。国内外很多学者均开展了较为系统的研究。目前塔线体系风荷载效应的研究主要是从普通季风、龙卷风、下击暴流、强台风等几个方面开展。在输电塔季风荷载效应方面，Tsui[108]、Mathur 等[109]、Liew 和Norville[110]、Yasui 等[111]较早开展了相关工作，他们采用不同方法研究杆塔的风致响应的特点和规律。进 一 步 地，Battista 等[112]、Loredo-Souza 和Davenport[113]研究了季风作用下的塔线体系动力耦合效应、阵风因子及杆塔抗风设计方法等。此外，各国学者还研究了不同地貌地区、不同结构参数、不同类型输电杆塔的风致响应特点及抗风设计方法等输电塔线体系风致响应问题[114-115]。国内这方面的工作虽晚于国外，但由于我国学者的努力，也开展了很多的工作如：李宏男等[12,116]、李正良等[117]、沈国辉等[118]、陈政清等[90]、瞿伟廉等[4,119-120]、梁枢果等[121]、李黎和尹鹏[122]、邓洪洲等[123]、刘春城[124]、张林林和李杰[125]、何敏娟等[126-128]，很多研究成果已经居于国际先进水平。

输电杆塔强风荷载效应方面，由于实测、实验困难以及相关基础理论的不完善，研究工作相对于季风荷载效应要少得多。Savory 等[129-130]研究了龙卷风作用下的输电导线的风荷载和风致振动问题。Ahmed 等[131]研究了龙卷风下输电杆塔的损伤破坏问题。Pecin 等[132]基于龙卷风响应谱研究杆塔的风致响应。Shehata 和Damatty[133-135]系统研究了输电杆塔和导线在下击暴流作用下的风荷载和风振响应问题。Li[136]、Darwish 和Damatty[137-138]通过参数研究考察了不同下击暴流类型和不同结构参数下输电杆塔的风振特性。国内众多学者也研究了下击暴流作用下的输电杆塔动力响应和倒塌问题[4,139]。由于实测和试验模拟的困难，输电塔线体系台风荷载效应的研究则更少[140-141]。总体而言，目前国内外在输电塔线体系风致效应方面的研究主要集中于季风荷载方面，在强风荷载效应方面的研究工作还很欠缺。我国主要自20 世纪八九十年代开始开展相关研究工作，目前研究水平与国外基本相当。

输电塔线体系的地震灾变效应研也是研究热点之一[142-147]。早期工作主要侧重于考察输电塔线体系的地震响应和塔线体系偶联效应，后期逐渐过渡到研究近场、远场地震效应以及非一致激励地震响应方面。近年来，针对输电塔线体系在地震作用下的倒塔破坏模式和损伤特点的研究也有相关开展[148-151]。由于在高海拔湿冷地区多发输电线路覆冰断线灾害，因此相关的研究工作也受到了很多重视。我国的相关研究工作开展晚于国外，但也取得了很多研究进展[152-153]。沿海强风地区多发的风致断灾害也受到了很多关注，相关的研究工作也有很多，其主要思路是基于输电塔线体系的模型研究断线对杆塔的动力冲击效应以及输电线的跌落效应[154-156]。利用输电塔线体系力学模型开展的防灾减灾的研究工作中还有一个非常重要的内容即为输电塔线体系的减振控制[6,157-159]。这方面的研究也已开展了较长时间，主要是针对风振和地震响应的控制[160-163]。相关研究工作具有几个非常明显的特点：1)多数工作为塔线体系的风振控制；2)减振控制方法较为类似，基本是采用被动耗能阻尼器、动力吸振器类减振装置；3)研究工作绝大部分以理论研究和数值模拟为主，控制装置实际应用很少。

5 结论

本文综述了国内外输电塔线体系力学模型的发展现状和技术要点。还简要评述了不同输电线模型、输电塔模型以及塔线体系模型的优缺点及适用范围。本文主要结论如下：

(1) 输电线的力学模型是塔线体系力学模型的核心。输电线的杆系模型概念明确，表达式简单，参数少且易于建模，为众多商业有限元软件所采用。但由于梁单元或杆单元模型无法充分考虑初始应变和初始位移等引起的输电线强几何非线性效应，因此计算精度有限，特别是对于大垂度输电线的分析精度不佳。

(2) 基于Hamilton 原理发展起来的多质点模型具有简洁高效的优点。但由于对输电线采用了等价线性化处理，因此对输电线的非线性效应模拟精度有限。后期发展起来的基于多节点索单元的输电线力学模型具有精度高、适用面广、适用性好等一系列优点。但由于隐式刚度矩阵计算需大量积分运算，因此该模型效率低下，不便于大规模工程应用。基于显式索单元的输电线力学模型有效地克服了上述模型的缺点，同时兼顾了计算精度和分析效率，非常适合于实际工程应用，具有广阔的应用前景。

(3) 随着输电线路防灾减灾发展，对其服役性能的精细化监测评估越来越受到重视。因此，针对输电线股线层级的精细化力学模型和精细分裂导线力学模型的需求将不断增加，这也是未来输电线性能评估的重要方向之一。

(4) 目前商业有限元软件所广泛采用的输电塔线体系杆系有限元模型具有建模简单快捷的优点，但对输电线的非线性动力响应模拟精度还需进一步提升。而基于精细索单元的塔线体系模型虽然具有很高分析精度，但操作复杂、不便于实际工程应用。因此，基于高精度索单元发展高效精确、易于使用的输电塔线体系力学模型仍然值得进一步深入研究，这也是输电线路防灾减灾未来的重要研究课题之一。