水平渗流作用下无黏性土接触冲刷细颗粒起动机理分析

2021-05-25梁发云

工程力学 2021年5期

张力，梁发云，王琛

(1. 同济大学岩土及地下工程教育部重点实验室，上海 200092；2. 同济大学地下建筑与工程系，上海 200092)

土石堤坝是重要的防洪构筑物，一旦溃决，将导致不可估量的损失。内部侵蚀是堤坝内部土颗粒被渗流带出的现象，是导致堤坝发生局部塌陷与失稳破坏的主要因素之一[1-2]。接触冲刷为其中一种，由平行于粗-细粒层界面的渗流引起[3]。接触冲刷导致细粒土在渗流作用下通过粗粒土孔隙冲出，会引发堤坝局部塌陷。美国的Teton 坝溃决系由坝基与心墙之间发生接触冲刷而导致心墙开裂造成的[4]；我国的沟后面板砂砾石坝由于坝体砂砾石填料严重分离而引发接触冲刷，最终诱发溃坝事故[5]。

接触冲刷的发生需要满足两个条件：几何条件和水力条件[6]。几何条件指粗粒层中的孔隙允许细粒土通过；水力条件是指渗流作用能够使细粒土被带出。对于几何条件，目前工程实践中一般认为，粗-细粒层的特征粒径之比(D10/d10)不大于10 时接触冲刷不发生[7]。对于水力条件，Иcтoминa[8]通过无黏性土接触冲刷试验的经验得到临界水力梯度与(D10/d10)tanφ的关系。Гoлбьдин等[9]认为接触冲刷的发生条件为细粒层特征粒径di与粗粒层孔隙直径D0之比小于0.7 且渗流雷诺数小于20。刘杰[10]总结分析前人试验结果，提出了无黏性土临界水力梯度的经验公式。陈群等[11]、朱亚军等[12]分别针对砂砾石与砂、砂砾石与黏性土开展了水平和竖向渗流条件下的接触冲刷试验，分析了几种不同水力梯度条件下对应的细粒土渗蚀程度。除模型试验外，计算接触力学方法和离散元法也被用于材料细观性质和物理过程的模拟[13-14]。常利营等[15-16]采用离散元方法，从细观上研究了接触冲刷的发生机理。

上述文献主要根据试验数据提出临界水力条件的经验公式，通常仅考虑粗-细粒土粒径之比，无法从细观上描述粗、细粒层接触面(以下简称“接触面”)上可动细粒土的起动机理。从细观上看，接触冲刷是渗流水产生的拖曳力使细粒土克服自重和粒间阻力运移而发生的。陶同康等[17]对水平渗流作用下接触面上的细粒土进行受力分析，根据力矩平衡推导出了无黏性土接触冲刷临界水力梯度(以下简称Jh,cr)的计算公式。邓伟杰[18]构建了砂砾石与黏性土间发生接触冲刷的细观模型，得到黏性土接触冲刷Jh,cr计算公式。然而，上述研究在推导过程中仅基于力矩平衡，始终假定可动细粒土为球形，缺乏实际接触面上细粒土粒径的分布特征以及起动位置特征的试验支撑。

本文依据无黏性土接触冲刷试验中接触面细粒土的粒径分布特征和可动细粒土的起动位置，针对上部为粗粒层、下部为细粒层的无黏性土层，对水平渗流条件下接触面上可动细粒土进行受力分析，建立了可动细粒土滑动失稳和滚动失稳的分析模型，推导了两种失稳模式下的Jh,cr计算公式，并通过试验数据对本文提出的公式与已有经验公式进行了对比分析。

1 接触面可动细粒土力学分析

无黏性土属于单粒结构，在接触冲刷条件下，发生失稳的是单个土颗粒。水平渗流作用下，当渗流作用使得接触面上的细粒土克服自重和粒间约束而运移时，接触冲刷发生。

1.1 接触面可动细粒土细观失稳模式

假设土体满足接触冲刷发生的几何条件，即粗粒层中的孔隙允许细粒土通过。此时，可动细粒土主要受水下自重W、渗流引起的拖曳力FD、颗粒侧压力FN和粒间摩擦力Ff的作用。由于实际堤坝工程中流场复杂，可动细粒土可能受到竖直向上的渗流产生的上举力FL，但在水平渗流条件下，上举力产生的作用较小，可以忽略[19]。

无黏性土接触冲刷的细粒土一般为砂土，其粒径较小且磨圆度较好，可先假定接触面处的可动细粒土为球体。滑动和滚动两种失稳模式中的失稳驱动力均为拖曳力FD，阻力来自重力W和粒间摩擦力Ff，其可动细粒土的受力如图1 所示。

图 1 可动细粒土失稳运动模式Fig. 1 Instability mode of removable fine particles

参考江胜华等[20]提出的块石滑动失稳条件，可动细粒土的滑动失稳条件可由下式确定：

在滚动失稳模式下，如图1(b)所示，Q点为该过程的转动中心，由此建立滚动失稳条件如下：

式中：FD为可动细粒土所受拖曳力；W为可动细粒土水下重力；f为可动细粒土与其他土粒之间的摩擦系数；FN为可动细粒土侧压力；Ff为粒间摩擦力；β1、β2、β3、β4分别为拖曳力、可动细粒土水下自重、可动细粒土侧压力和粒间摩擦力的力臂系数，与可动细粒土形状和颗粒接触位置有关，取值范围是0～1；di为可动细粒土的粒径。

可动细粒土水下自重W的计算见式(3)。渗流引起的拖曳力FD和颗粒侧压力FN由式(4)和式(5)确定[17]。粒间摩擦力Ff由式(6)确定。

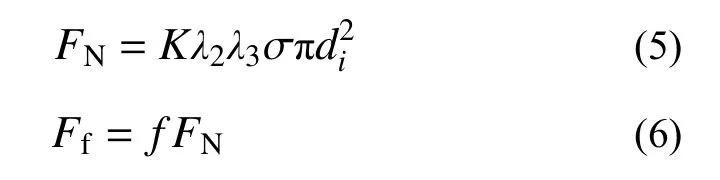
式中：γs为土粒重度，一般为26.5 kN/m3～27.5 kN/m3；γw为水的重度，一般为9.81 kN/m3；τ 为粗-细粒层接触面处的流动切应力；λ1为与流体流动切应力作用面积相关的修正系数；σ 为可动细粒土所处接触面上的竖向有效应力；λ2是与竖向有效应力作用面积相关的修正系数；λ3是与可动细粒土两侧侧压力作用面积相关的修正系数；K为侧压力系数。

1.2 接触面流动切应力

粗粒层的渗透系数大于细粒层，渗流流速也大于细粒层中的流速。因此，在包含接触面的一定区域内存在流速过渡区，在此过渡区内，流速由细粒层中的较小流速v2过渡到粗粒层中的较大流速v1，如图2 所示。

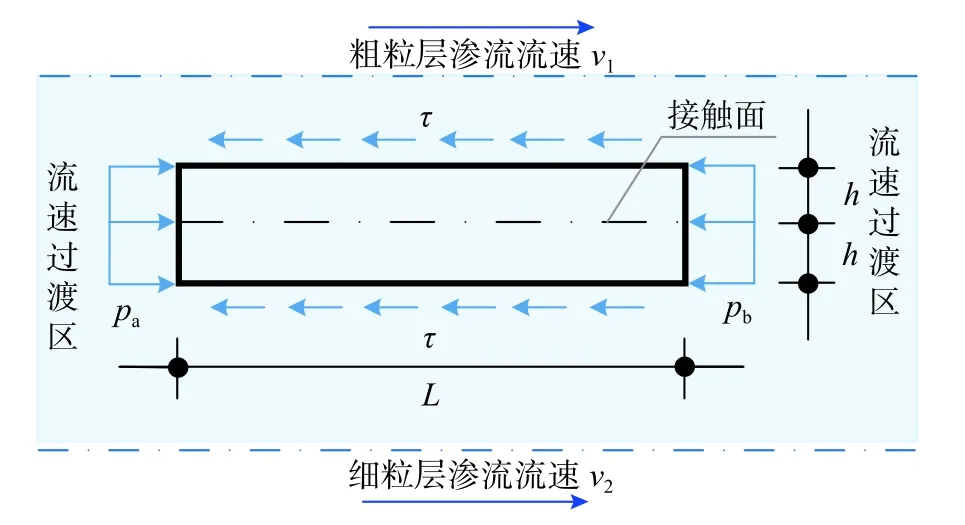
图 2 接触面隔离体受力分析Fig. 2 Force analysis of isolator at interface

细粒层的渗流速度小，流态通常可认为是层流；粗粒层中土颗粒粒径较大，流态为紊流状态，但根据紊流理论，水流在流体边界会形成边界层，在边界层内仍呈层流状态[21]。在接触冲刷发生前，土骨架和流场较为稳定，流体属于牛顿流体。因此，在包含接触面在内的一定区域内，渗流流态均可视为层流。

在包含接触面的层流区域内，以接触面为对称轴，取长为L、宽为1、高为2h的流层隔离体，如图2 所示。流层隔离体为一薄层，可认为隔离体两端静水压力为均匀分布，上、下表面的流动切应力均为τ。同一薄层的相邻隔离体间无相互作用[22]。由于接触面上、下均为土颗粒，实际隔离体上、下表面并非平面，上表面为隔离体内粗粒土表面积Ss,D，下表面为细粒土的表面积Ss,d。隔离体两端的静水压力差2y(Pa-Pb)与上、下平面的摩阻力之和互相平衡[17]，由力学平衡条件可得：

假设粗-细粒土均为直径统一的球体，总体积为V的土体内土颗粒体积Vs和土颗粒面积Ss见式(8)和式(9)，土颗粒体积Vs与总体积V之间关系见式(10)，联立可得体积为V的土体内土颗粒表面积如式(11)所示。

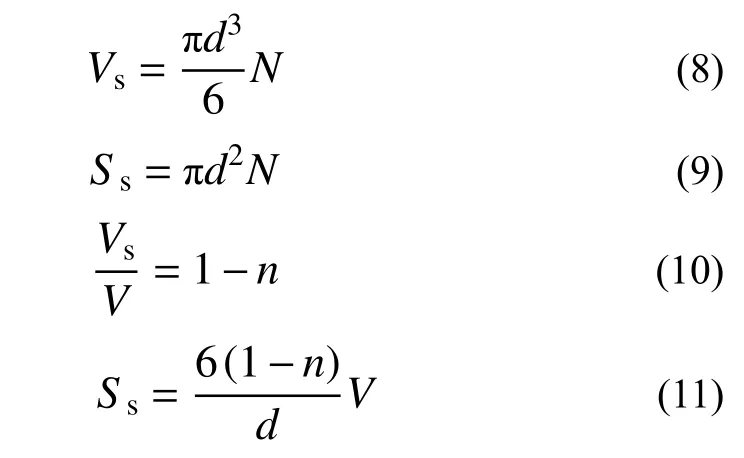
式中：d为土颗粒直径；N为单位体积内土颗粒的个数；n为孔隙率；Vs为土颗粒体积。

土体通常由多粒组构成，粒径并不统一。对于一定级配范围的同类土，采用等值粒径dκ代替d计算土粒面积Ss，由式(12)确定dκ。结合式(11)和式(12)，隔离体内粗粒土表面积为Ss=6Lh(1-n1)/Dκ，细粒土表面积为Ss=6Lh(1-n2)/dκ。

式中：dj为第j粒组的代表粒径；Fj为第j粒组的质量百分含量。

实际上，土颗粒并非完全规则的球形，因此，需要对隔离体内的土颗粒表面积Ss乘以形状修正系数α，结合式(7)、式(11)和式(12)可得流层隔离体上、下表面摩阻力之和为：

式中：下标1、2 分别代表粗粒层、细粒层；Dκ、dκ分别表示粗粒层、细粒层的等值粒径。

根据流层隔离体的力学平衡式(7)得到接触面附近的流动切应力τ 为：

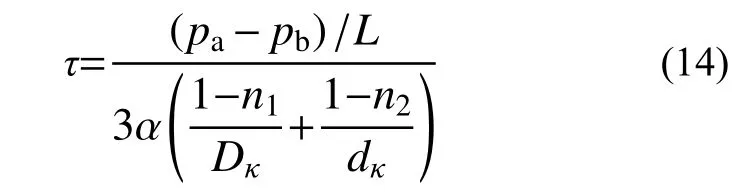
水平水力梯度Jh与隔离体两端的静水压力关系如下式所示：

式中：ΔH为沿渗流路径的水头损失；ΔL为渗透路径的长度。

将式(15)代入式(14)，可得由水平水力梯度Jh表达的接触面流动切应力τ 的计算式：

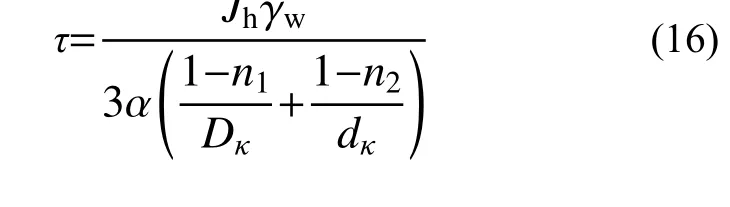
2 临界水力条件分析

2.1 可动细粒土滑动失稳

当可动细粒土滑动失稳，将式(3)～式(6)、式(16)联立并代入式(1)中，得到该失稳状态下的条件应满足：

式中，Jhs,cr为滑动失稳时的临界水力梯度，其计算式如下：

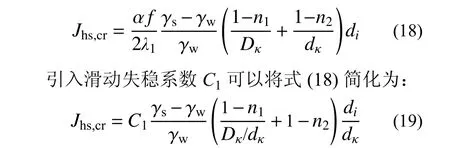
式中，系数C1=αf/ 2λ1，与颗粒形状及其与周围颗粒的接触方式有关。

2.2 可动细粒土滚动失稳

当可动细粒土滚动失稳时，将式(3)～式(6)、式(16)联立并代入式(2)中，得到该失稳状态下的条件应满足：

本文采用与Liang 等[23]研究中相同的试验条件来分析接触面细粒土的起动特征，研究发现，最先起动的可动细粒土位于粗颗粒间的孔隙。在玻璃珠与砂的试验组中，细粒土起动最先发生于试样接触面入水端的玻璃珠孔隙处(图3)；在石英砂和砂的试验组中，仅是位于石英砂孔隙较大处的细粒土发生了局部运移，位置1 处的可动细粒土运移到位置2 处(图4)。综上得到，位于接触面粗粒土孔隙处的可动细粒土上覆有效应力为0，即σ = 0。引入滚动失稳系数C2，式(21)可简化为：

式中，系数C2=αβ2/2β1λ1，与颗粒的形状及其与周围颗粒的接触方式相关。

图 3 玻璃珠与砂接触面细粒土起动Fig. 3 Entrainment of fine particles at interface between glass beads and sand

图 4 石英砂与砂接触面细粒土起动Fig. 4 Entrainment of fine particles at interface between quartz rubbles and sand

从式(19)和式(22)可以看出，接触面上可动细粒土滑动失稳或滚动失稳的Jh,cr均可表达为：

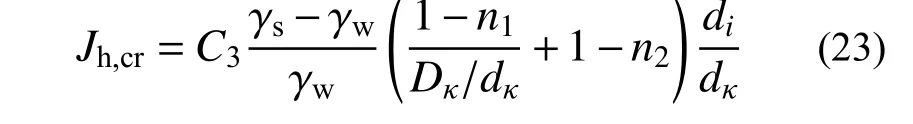
式中，失稳系数C3是与颗粒形状及颗粒接触方式有关系数，难以精确计算，可通过试验结果确定。

2.3 系数确定

Cyril 等[24]对粗粒土在上、细粒土在下的土样开展了接触冲刷试验，得到多组Jh,cr的试验值，试验结果如图5 所示。本文采用Cyril 等[24]得到的粗粒土C1～C4 与砂土B6 的接触冲刷试验数据来确定系数C3，土样物理指标见表1，试验得到的Jh,cr见表2。由于砂土B6 级配良好，取可动细粒土直径di=dκ，由式(23)可得系数C3，见表2 所示，通过线性回归可得C3=4.23d50/D50，如图5 所示。Jh,cr可由式(24)确定。

图 5 系数C3 与粗-细粒径比d50/D50 的线性回归Fig. 5 Linear regression of coefficient C3 and particle size ratio d50/D50

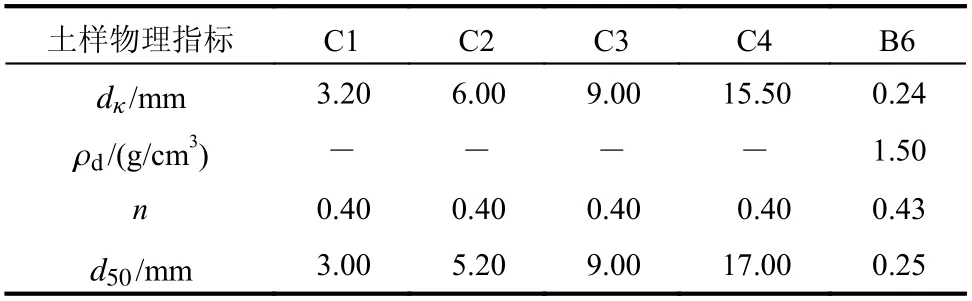
表 1 土样物理指标[24]Table 1 Physical properties of test soil

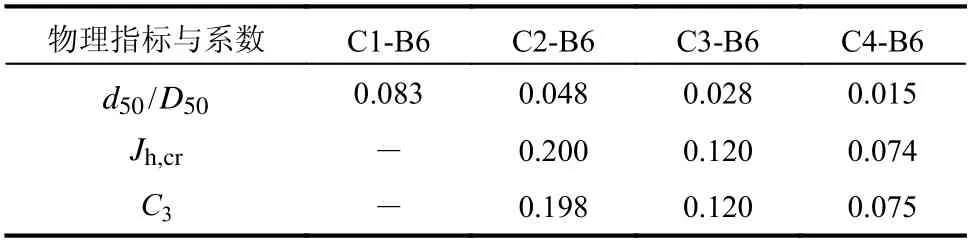
表 2 水平临界水力梯度与系数C3Table 2 Critical horizontal gradients and coefficient C3

3 算例分析

接触冲刷的发生需要满足几何条件和水力条件，判别流程如图6 所示。几何条件是土体的内在因素，水力条件是土体面临的外在因素。

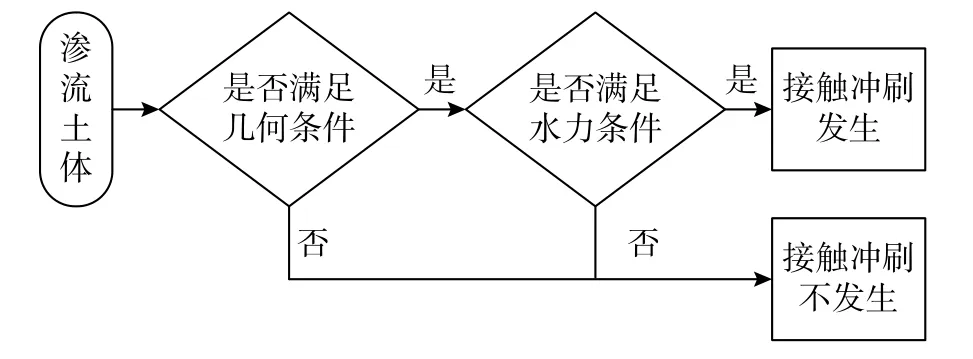
图 6 接触冲刷发生与否判别流程Fig. 6 Judgement of occurrence of contact erosion

3.1 Liang 等[23]无黏性土接触冲刷试验

Liang 等[23]对2 种土样进行了水平渗流条件下的接触冲刷试验，分别为上部石英砂和下部砂土，以及上部玻璃珠和下部砂土的不同情况，本文将其得到的Jh,cr试验值与式(24)得到的计算值对比分析。

对于石英砂和砂试验组，由于土样不满足几何条件，接触冲刷未发生。对于玻璃珠和砂的试验组，土样满足接触冲刷的几何条件，接触冲刷发生，接触冲刷水平临界水力梯度的试验值为0.60～0.62。

根据图7 中试样接触面粒径分布和砂土试样的对比以及试验用土的级配，取可动细粒土直径di=d50= 0.72 mm，Jh,cr理论计算的相关数据见表3。

图 7 玻璃珠和砂接触面细粒土粒径分布以及砂土试样Fig. 7 Fine particle distribution at interface between glass beads and sand

表 3 试验土样的物理性质指标[23]Table 3 Physical properties of test soil

将表3 中的数据代入式(24)得Jh,cr理论计算值为0.55，与试验值0.60～0.62 比较接近。

3.2 刘杰[10]无黏性土接触冲刷试验

将本文推导得到的Jh,cr计算公式与刘杰[10]提出的经验公式进行对比分析。假设细粒土为Liang 等[23]采用的福建标准砂，粗颗粒土为单一粒径土，即D50=D20=Dκ，取粗粒层孔隙率n1=0.4[24]。取可动细粒土粒径di分别为d50= 0.72 mm 和d15=0.13 mm，Jh,cr与粗、细粒径之比D/d的关系曲线如图8 所示。

由本文公式计算的Jh,cr随D/d增大而减小的趋势与刘杰经验公式所得结果一致，但刘杰经验公式无法考虑接触面上细粒土粒径分布特征，这点在本文公式中得到了改进。Liang 等[23]接触冲刷试验选用的福建标准砂为间断级配且细粒组含量较小的砂土，标准砂中的细粒组易通过颗粒间的孔隙滑落至土样下部，使得分布在接触面上的土颗粒以标准砂中的粗粒组为主，故取可动细粒土粒径di=d50，结果表明本文公式求得的Jh,cr与试验数据较为一致。Cyril 等[24]与Иcтoминa[8]试验所用细粒土均为级配良好的砂土，接触面上细粒土的特征粒径d10在0.10～0.16，取可动细颗粒粒径di=0.13 mm，该值恰好等于福建标准砂特征粒径d15，根据本文公式计算得到di=d15时的Jh,cr曲线如图8所示，与两位学者的试验结果较为一致。综上所述，本文Jh,cr计算公式有所改进之处在于，可以根据接触面上细粒土粒径分布特征选取可动细粒土粒径值，使得计算结果更贴近实际。

图 8 水平临界水力梯度与粗-细粒径比关系曲线Fig. 8 Calculated critical horizontal gradient versus particle size ratio

需要注意的是，可动细粒土粒径di取不同特征粒径值时，采用本文公式计算得到的Jh,cr差异较大，如图9 所示。采用该公式计算Jh,cr时，若di取值比实际值大，将导致Jh,cr计算值偏大。此时，实际水力梯度尚未达到Jh,cr计算值时，接触冲刷便已发生。特别地，若取可动细粒土粒径di为d85时，试验数据位于曲线下方，偏不安全；若取可动细粒土粒径di为d15时，试验数据位于曲线上方，偏保守。因此，可动细粒土的粒径di需根据接触面上细粒土粒径分布特征准确选取。

图 9 不同可动细粒土粒径下水平临界水力梯度与粗-细粒径比关系曲线Fig. 9 Calculated critical horizontal gradient versus particle size ratio with different removable fine particle sizes

当D/d≤10 时，接触冲刷不发生[7]。当10＜D/d＜50 时，Jh,cr主要受D/d和di的影响，特别是D/d＜20 时，Jh,cr变化率较大，主要是由于此时粗粒土间孔隙相对较小，当孔隙进一步减小，孔隙对流体的阻力急剧增大，导致颗粒起动所需的水力梯度明显增大。特别是当di较大时，颗粒起动所需的拖曳力较大，即所需渗流流速更大，由达西定律可知，接触冲刷所需的水力梯度也越大，此时，若粒径比变小，Jh,cr的变化会更为明显。当D/d＞50 时，Jh,cr随D/d增大的变化较小，受di的影响较大。因此，接触面上细粒土的细观粒径分布特征对Jh,cr有重要影响，当分布特征未知时，可采用d15作为可动细粒土粒径di。如果细粒土为间断级配砂土，粗、细粒组分离，采用d15作为di计算时的结果会偏保守。

不同粗粒层孔隙率n1下水平临界水力梯度Jh,cr随粗-细粒径比D/d的变化曲线如图10 所示，不同粗粒层孔隙率n1对应曲线较为接近，最大差值不超过0.06。但结果仍一定程度上表明，粗粒层孔隙率n1越大，水平临界水力梯度Jh,cr越小，可认为水平临界水力梯度Jh,cr与粗粒层孔隙率n1成负相关，但是n1对Jh,cr的影响较小。