泡沫清管器过盈量计算及其对清管效果影响
2021-05-25刘建林徐香玲程永桂
刘建林, 徐香玲, 程永桂, 张 云
(中国石油大学(华东)储运与建筑工程学院,山东青岛 266580)
在世界能源开发领域,油气在一次能源中所占的比例高达一半以上,且此数据持续增长,具有极好的发展潜力[1-3]。世界各地油气需求的快速增长促进了油气输送管道与区域配送管网的快速发展,使得油气管道在日常生产生活中的作用显得日益重要[4-9]。但与此同时,随着管路的增多、管龄增长和输送压力提高,油气管道在长久运行之后会出现管道结垢、杂质黏附等,从而引起一系列管道故障问题。这些管道故障会极大地影响其运输效率,甚至会造成管道堵塞和腐蚀[10]。目前在管道清洗方面存在的最大问题是在特定环境下清管效果并不明显,需要研发更加符合工程实际的清管工艺。工程中最常见的清管技术是采用清管器进行清理[11-13]。其中泡沫清管器由于具有密封性好、重量低、磨损率低、不易卡堵等优点,已成为应用最广泛的清管器之一[14-16]。该类清管器的工作原理为:清管器与管道之间实现了过盈配合,从而形成密封以隔绝前后流体,由此在清管器前后造成压力差,该压力推动清管器运行[17-18]。已有大量研究者研发了多种类型的清管器。Short[18]在一份工程报告中指出,尽管工业界已经在清管实践中积累了很多现场经验,但很难依据于此来优选清管器,目前对清管机制和清管过程中清管器的受力认识严重不足。Lino等[19]在试验环道上进行了大约800次清管实验,但是并没有得到任何具有借鉴意义的数据。Mendes等[20]首次对清管器的运动规律进行了研究,认为若清管器与管道内壁之间存在间隙,会使流体在清管器前后压差的驱动下进入间隙,从而会影响管壁与清管器之间的相互作用。在研究过程中发现,过盈量的设计对于清管器的正常工作具有至关重要影响。如果过盈量过大,可能会造成清管器的卡堵现象;过盈量过小,则会影响清管效果。韦永金等[21]指出,目前检测管道是否堵塞并进行清管的常用工具是聚氨酯泡沫清管器。但是由于管道内部情况复杂,结垢的分布及厚度情况未知,清管过程极为繁杂,需要多次投放聚氨酯泡沫清管器,因此极有必要对泡沫清管器的半径或者过盈量给出预测。陈浩等[22]发现清管器皮碗与管道之间的最大接触应力与二者之间的相对过盈量近似呈线性增长趋势,但是该工作未进行更进一步的理论计算并得到更为精确解答。Wang等[23]和王文达[24]设计了一种室内模拟清除油蜡混合物的实验装置,测试得到不同清管器硬度等条件下剥离蜡沉积物所需要的力,拟合得到关于剥离蜡沉积物所需施加力的经验公式。但是,由于其公式是纯经验公式,所以该方法尚未得到广泛推广。黄飞扬等[25]对清管器运动过程中的磨损机制进行了探究。戴斌等[26]和臧延旭等[27]的研究均指出,对于皮碗式清管器,过盈量过大会导致清管器皮碗的严重磨损,故而皮碗过盈参数的选取对于建立清管器皮碗的力学模型至关重要。此外段瑞溪等[28]对具有不同过盈量的多相流管道中的清管过程进行模拟实验,发现在长距离管道清管过程中,若旁通性较大(或过盈量较小),可能会使清管器失去清管效果。这些研究工作大都将清管器-管道结构作为一个整体进行探究,对二者之间相互作用的定量计算相对较少。笔者以泡沫清管器和其配合的管道为研究对象,建立3种模型,并对工程中常用的钢管及聚氨酯泡沫材料组成的清管器进行过盈量求解。采用有限元对管道内壁存在污垢的情况下进行模拟,分析具有不同过盈量清管器的清洗结果。
1 清管器过盈量计算
在实际工程中,为了实现较好的清管效果,泡沫清管器与管道一般都是进行过盈配合,在此过程中管道内壁和清管器都会产生挤压力。如图1所示,设管道内半径为r1,外半径为r2,泡沫清管器半径为r3,则相对过盈量可以定义为δ=(r3-r1)/r1,并且令管道与清管器之间的相互作用力为q(单位面积上的压力)。目前的设计手册中并没有明确给出这一过盈配合过程的弹性力学模型,其解析解更未给出,从而给工程设计带来一定困惑。分别采用平面应变模型、平面应力模型、空间轴对称模型以及数值模拟方法对此问题进行研究,并对计算结果进行全面对比,以筛选出适用于工程实际的模型。
1.1 平面应变解答
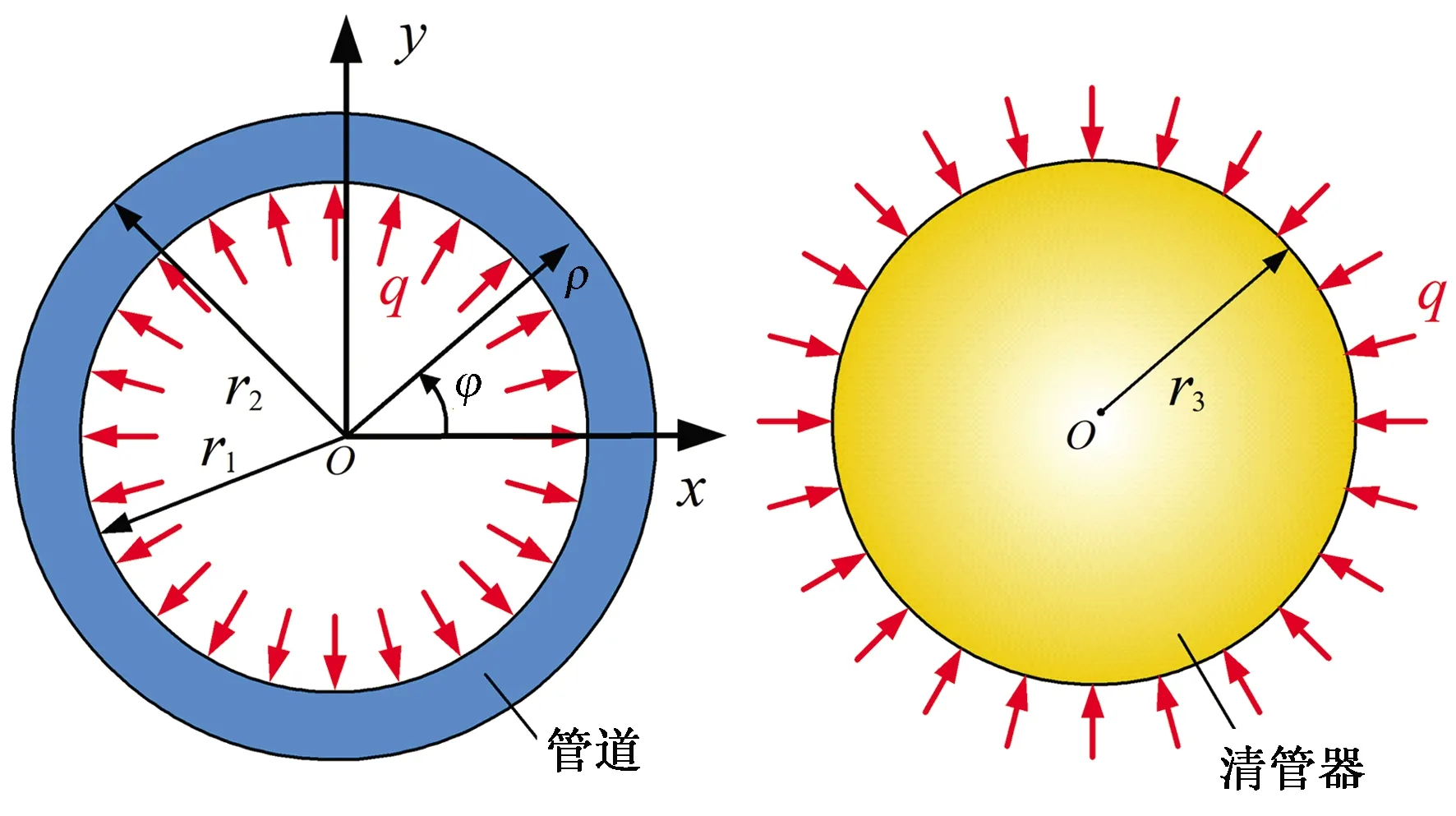
图1 管道及清管器受力示意图(侧视)Fig.1 Schematic of pipeline and pig (side view) under loads
如图1所示,在实际工程中,油气管道一般为轴对称结构,由于其长度较大,故此首先考虑采用平面应变模型进行简化解答。建立图示的极坐标系O-ρφ,其中ρ为任意一点的径向长度,φ为环向角度。管道内壁承受均布压力q,清管器外表面也承受同样大小的载荷。设管道弹性模量与泊松比分别为E1和μ1,清管器弹性模量和泊松比分别为E2和μ2。
对于平面问题的轴对称结构,可选择轴对称应力函数φ的通解为
φ=Alnρ+Cρ2+D.
(1)
式中,A、C、D为待定常数。
则应力分量为
(2)
进一步可以推得径向位移分量为
(3)
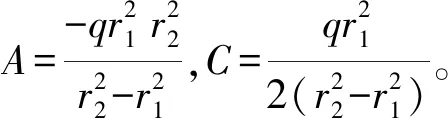
由此可以得到管道内壁的位移量为
(4)
对于清管器,其应力边界条件为ρ=r3,σρ=-q,则可以求得对应系数C=-q/2。
从而可以得到清管器外侧面的位移分量,表示为
(5)
由管道和清管器之间的变形协调关系可得
r1+u1ρ(r1)=r3+u2ρ(r3).
(6)
最终可以得到清管器和管道之间的相互作用力,表示为
(7)
1.2 平面应力解答
由于清管器两端自由,故此可以尝试采用平面应力模型进行分析。基于此假设,轴对称问题的径向位移解答为
(8)
则可以得到管道内壁的位移分量为
(9)
清管器外壁的位移分量为
(10)
结合变形协调关系可得到相互作用力为
(11)
1.3 空间轴对称解答
考虑到管道和清管器均为轴对称结构,但其纵向有一定长度,故此另外一个更加符合实际的模型即为空间轴对称模型。如图2所示,建立柱坐标系,其中r为任意一点的径向长度,φ为管道横截面内的环向角度。
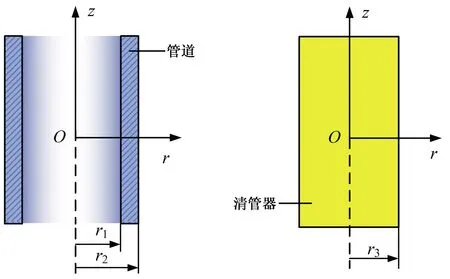
图2 圆柱坐标系示意图Fig.2 Schematic diagram of cylindrical coordinate system
首先对管道进行分析,其边界条件为
(12)
任意一点处径向位移为
(13)
其中
这一决策的提出,是依托当前信息技术时代“互联网+教育”的时代背景,对于教研工作的突破性创新,它能够克服时间、空间等不利条件的约束,利用网络技术,把小学数学教研工作落到实处。这首先需要做的就是要强化技术培训和相关网络知识的学习,能够使工作坊学员逐渐熟练工作坊研修操作平台,阅读研修须知,明确研修任务。当学员们掌握了平台使用和操作的基本技术之后,鼓励学员联系自己的数学教学实践积极地参加主题研讨、教学诊断、课例分享等研修活动,这样才能够保证研修活动的有效开展。
G=E/[2(1+μ)].
式中,G为剪切模量;Love位移函数φ(r,z)为重调和函数,需满足条件4φ=0,同时势函数φ(r,z)还需要满足位移边界条件和应力边界条件。
计算中选取符合上述条件的势函数为
φ=A1zlnr+A2z3.
(14)
式中,A1和A2为待定常数。
则应力分量为
(15)
(16)
式中,G1为剪切模量。
对于清管器,其边界条件为z=0,uz=0,τzr=0;r=r3,σr=-q。在任意一点处有σz=0。则选取符合边界的势函数为
φ=B1z3+B2zr2.
(17)
式中,B1和B2为待定常数。
其应力分量解答为
(18)
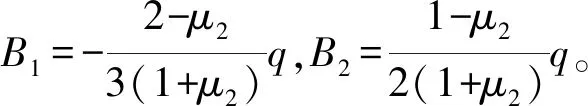
则可得到清管器径向位移为
(19)
式中,G2为清管器剪切模量。
泡沫清管器与管道之间变形协调关系为
r1+u1r(r1)=r3+u2r(r3).
(20)
则可以得到作用力q与过盈量δ函数关系为
(21)
1.4 模型比较
为进一步验证3个模型的有效性,开展有限元模拟,其结果对比如图3所示。
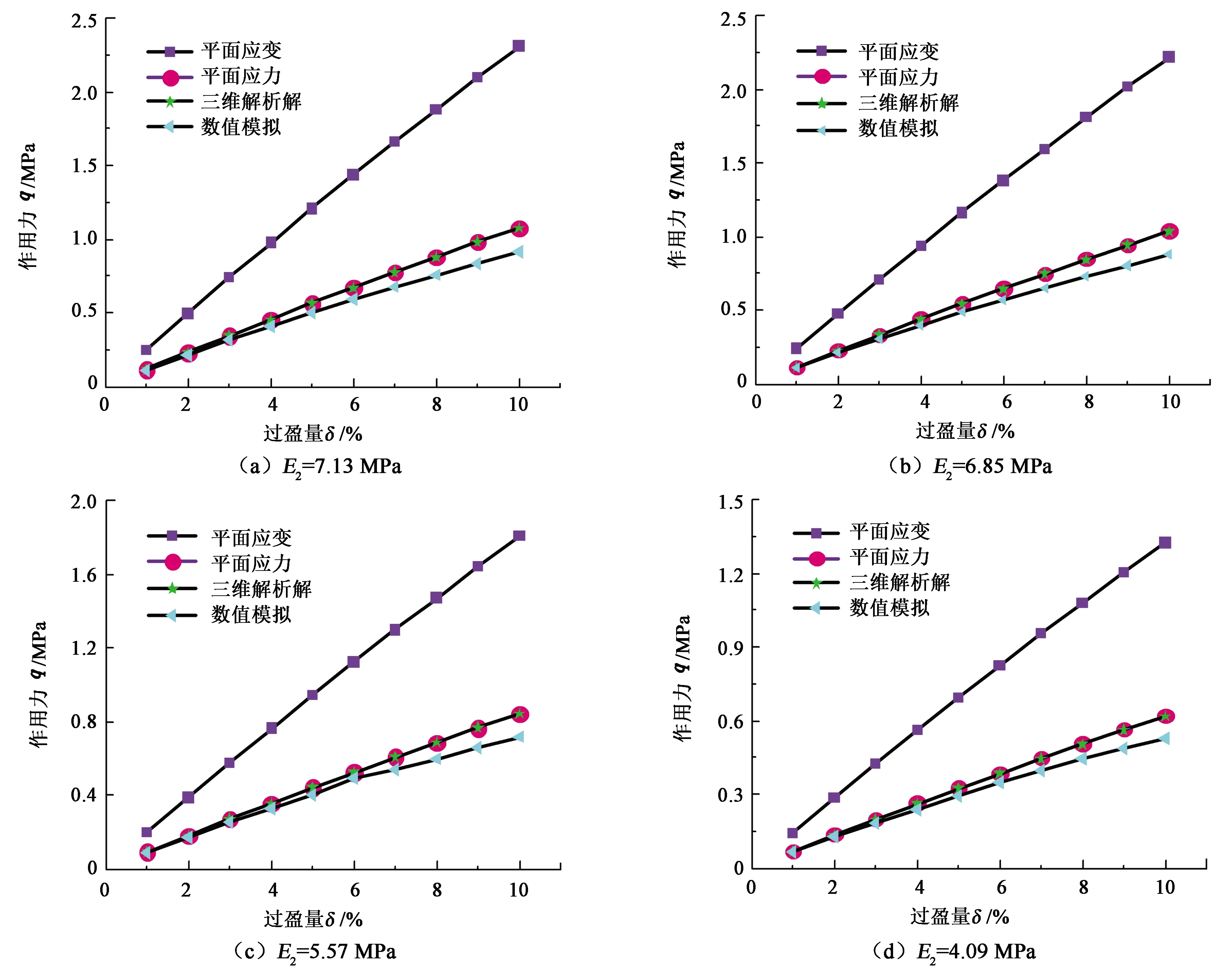
图3 四种不同清管器材料的接触力解答Fig.3 Contact force solutions for four kinds of pig materials
实际计算中,选取管道尺寸为Φ219 mm×6 mm,弹性模量E1为210 GPa,泊松比μ1为0.3。另外选取4种典型的聚氨酯泡沫材料,其弹性模量E2分别为7.13、6.85、5.57和4.09 MPa,泊松比为μ2=0.4。工程中要求的相对过盈量范围为1%~10%。
从图3中可见,3种解析模型所得到的解答与数值结果趋势一致,即相互作用力随着相对过盈量增大而增大,其曲线近似为直线形状。这是由于上述解析解表达式的分母中δ的系数接近于0,故而从量级上来看近似有关系q∝δ。另外,平面应力模型与三维空间解析模型的解答几乎重合,而此二者结果与数值解也比较接近。但是平面应变模型的解答与其余3个结果差别较大。这是由于现实中的管道并非无限长而且两端固定,故而并不严格满足平面应变模型条件,即轴向应变并不严格等于零。这一特点说明,在工程中对清管器结构进行建模分析时,不宜采用平面应变模型。
2 过盈量及其清管效果
2.1 过盈量及推力计算
在清管器实际运行中,它与管壁接触从而产生摩擦力。考虑到清管器在实际清管过程中一般保持匀速运行,因此推动力与摩擦力保持平衡,则有
2πR2p=πRlqfs.
(22)
其中
式中,R为装配之后的实际半径;fs为管道与清管器之间的动滑动摩擦系数;p为推动清管器前进的实际压强;l为清管器长度。
则公式(22)可以化简为
p=qlfs/(2R).
(23)
通过式(23),若给定外加推力,则可以求解泡沫清管器半径及过盈量。
计算中选取一些符合工程实际的参数:被清洗的管道Φ219 mm×6 mm,现场确定的压强为p=0.5 MPa,摩擦系数为fs=0.2。根据这些参数可以确定r1=103.5 mm,r2=109.5 mm。管道钢的弹性模量为E1=210 GPa,泊松比μ1=0.3。泡沫清管器采用的是聚氨酯发泡材料,可选取其中一种聚氨酯泡沫的弹性模量为E2=7 MPa,泊松比μ2=0.4,选取泡沫清管器的长径比为l/d=1.9,其中d为管道外壁直径,此处的d=219 mm,则近似选取清管器的长度为l=427 mm。将这些参数代入式(23),可以解出泡沫清管器的相对过盈量δ=2.82%,这个结果符合工程中经验公式的选取范围,即1%~10%。
由式(23)可以看出,推动力p与过盈量δ之间存在一定的函数关系。通过该平衡方程也可以得出一种确定施加推力的方法。例如计算中针对3组管道,其参数分别为DN200(Φ219 mm×6 mm)、DN400(Φ406 mm×10 mm)和DN600(Φ610 mm×14.2 mm),其中l/d=1.5。若δ=3%,则可求得此3组管道对应的推动力p分别为4.130 1、4.043 2和4.031 6 MPa。
需要说明的是,在实际工程应用中,泡沫清管器的设计尺寸并非固定,通常选择其长径比l/d的取值范围为1.3~2。仍然以 DN 200系列管道为例,选择长径比l/d分别为1.3、1.6和2,可以计算出所需要的推动力p,其结果如图4所示。由图4可见,推动力随着过盈量增大而增大,这说明过盈量较大时,其摩擦力较大,故而根据摩擦定律可知所需要的驱动力也相应变大。根据量级分析可知,外加推动力与过盈量之间的关系大致为p∝δ-2,此与图4结果是一致的。
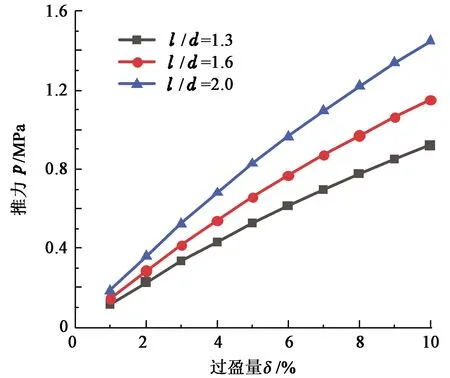
图4 三种不同长径比泡沫清管器对应的 过盈量与推力关系Fig.4 Relationship between interference and thrust of foam tube cleaner with three different aspect ratios
2.2 材料性质对过盈量影响
工程应用中油气管道的材料大部分为钢材,主要有碳钢、合金钢、铸钢等几种,它们的主要力学性能参数如表1所示。而聚氨酯泡沫清管器的弹性模量取值与图3的给定数值一致。
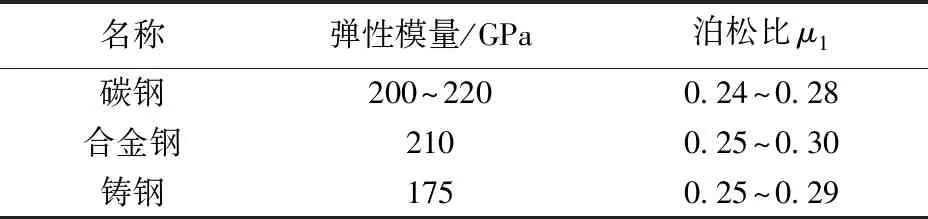
表1 工程管道常用材料参数Table 1 Normal material parameters of pipes in engineering
对工程中常用的碳钢进行分析。其弹性模量一般不是固定值,计算中取其泊松比μ1分别为0.24、0.25、0.26、0.27和0.28,则对应于4种典型的聚氨酯泡沫材料(与图3参数一致),对尺寸为Φ219 mm×6 mm的管道进行过盈量求解,所得结果如图5所示。
由图5结果可知,过盈量随着碳钢的弹性模量增大而变小,这说明钢管材料越硬,则其变形较难,故而过盈量较小。并且由图5可见,泊松比越大,过盈量越小。经过计算可知,对于碳钢管道和聚氨酯泡沫材料,对于给定的工程参数,求得的过盈量为2%~5%,符合工程上过盈量的变化范围。
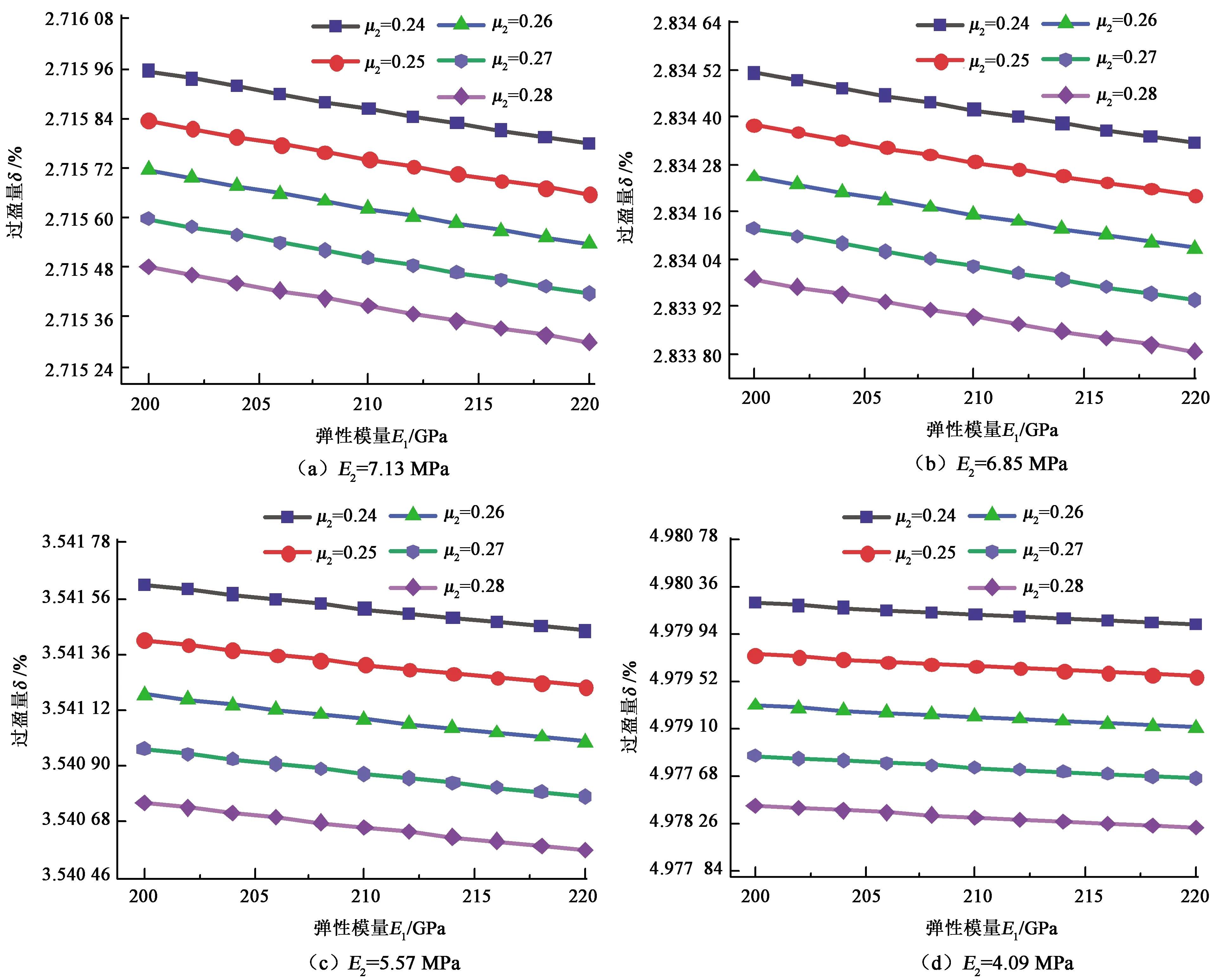
图5 碳钢材料管道-清管器结构的过盈量Fig.5 Interference of carbon steel pipe-pig system
对于合金钢和铸钢制成的管道,其弹性模量分别为定值210及175 GPa,其中合金钢的泊松比为0.25~0.30,铸钢的泊松比为0.25~0.29。经计算可知,过盈量对泊松比的变化并不敏感,其数值随着泊松比变化接近常数。但是过盈量受聚氨酯泡沫材料的弹性模量E2影响较大,当E2增大时,其数值变小。例如,取μ1=0.3,当弹性模量分别为7.13、6.85、5.57和4.09 MPa时,其过盈量分别为2.72%、2.83%、3.54%和4.98%。经计算可知,对于合金钢和铸钢制成的钢管与聚氨酯泡沫材料进行配合时,所得到的过盈量均在3%~7%之间,亦符合工程实际需求。同时发现,钢材弹性模量对于过盈量的影响远不如聚氨酯泡沫弹性模量对其影响,前者的变化范围约为10-6量级,而后者的变化范围则约为10-2量级。这是由于二者弹性模量的数值差异非常大,甚至达到104量级,也就是说二者材料软硬程度差别非常大。由此可见,在工程设计中,合理选择聚氨酯泡沫的材料参数对于得到理想清洗结果有重要意义。
3 过盈量对清管效果影响
采取有限元对清管过程进行数值模拟。在建模过程中,在管道内壁设置一层油蜡混合物,污垢密度为890 kg/cm3,动力黏度为260 mPa·s。采用一段管道进行模拟,管道内半径r1为103.5 mm,外半径r2为109.5 mm,污垢厚度t为20 mm。对3组不同半径的泡沫清管器(具有不同的过盈量)进行清管模拟,模拟速度均采用3 000 mm/s。模拟中的管道与清管器结构如图6所示。图中的红色区域表示污垢,设置为均匀厚度,蓝色区域表示管道内部空间。本次模拟采用ABAQUS软件,对于管道和清管器,定义为线弹性材料,选取其弹性模量和泊松比分别为210 GPa、0.3以及7 MPa、0.4。采用线性缩减积分计算,将管道及清管器分别划分为1 700个单元,此二者选择C3D8R网格单元,该网格能保证比较精确的位移结果。为符合实际情况需要,将污垢定义为欧拉体,采用Eulerian网格,该网格能够更好地观察到污垢的形态变化。此处将污垢划分为5 200个单元,定义其密度和动力黏度分别为890 kg/cm3及260 mPa·s,并定义管道内部空间均为污垢可能达到的区域。对于管道与清管器之间的接触设置,采取罚函数(Penalty)法,定义其摩擦系数为0.2。最后结合实际情况以及前面的计算结果,将管道两端设置为固定约束,清管器两端自由。模拟采用动态、显式(dynamic、explicit)分析步进行求解。
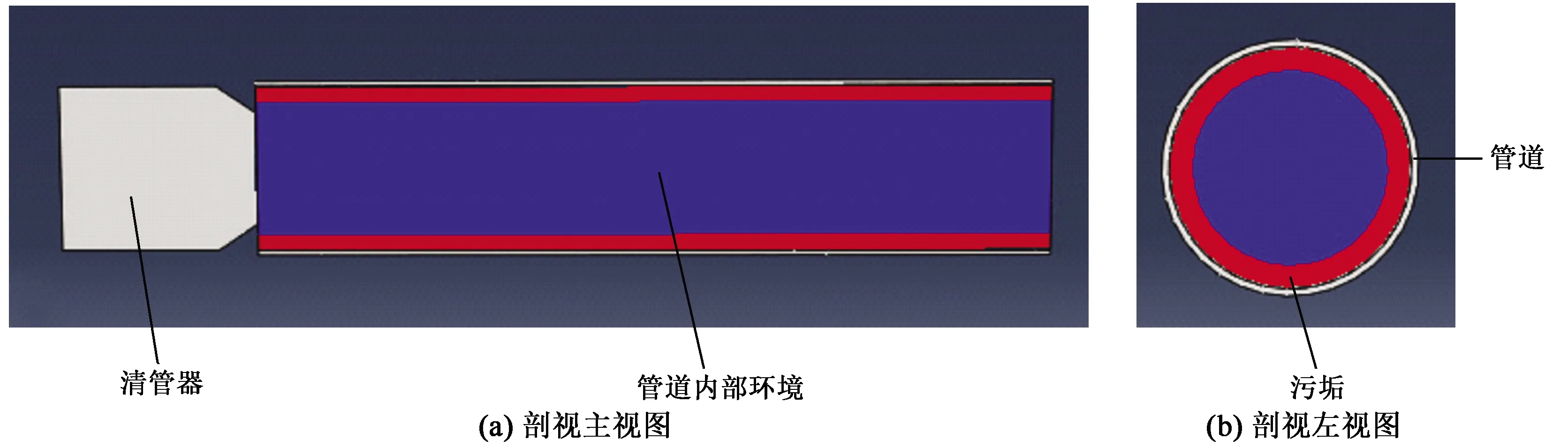
图6 清管器与管道配合Fig.6 Matching of pig and pipeline
考虑污垢存在,则此时的过盈量为δ=[r3-(r1-t)]/(r1-t)。首先考虑第一种情况,即过盈量δ=0,此时清管器外径与污垢恰好接触。当清管器从管道中通过时,此时的清管效果如图7所示。由图7可以看出,清管器通过管道后并没有将污垢完全剥离,只是对极少数的部分有清除作用,如图中黄色圆圈所示。此时清管之后的管壁中仍然有大量污垢,清管效果并不明显。
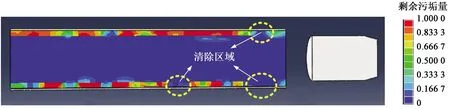
图7 清管器外壁恰好与污垢接触时的清管效果Fig.7 Pigging effect when outer wall of pig just contacts with the dirt
然后考虑第二种情况,即泡沫清管器与污垢直接接触,但有一定的旁通性,此时的过盈量取为δ=1.1%,其模拟结果如图8所示。由于所设置的污垢接近于流体,故此当清管器运行时会加强污垢的流动性,此时大部分污垢可以在管壁脱离,但是仍有一些污垢未能清除。这些残留在管道内部的污垢,还需要进行后续的清管工序才能驱走。
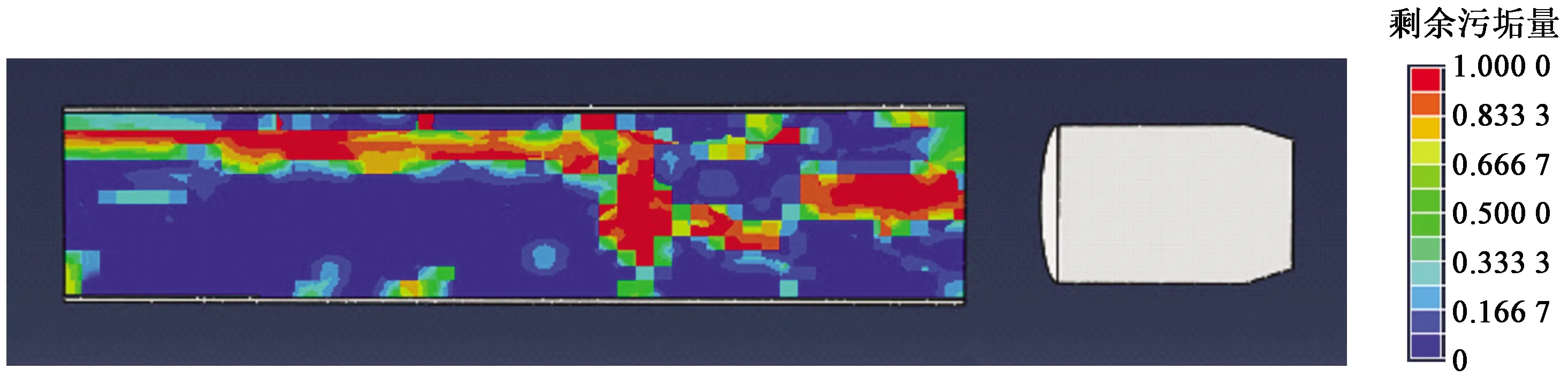
图8 旁通情况下的清管效果Fig.8 Pigging effect of bypass condition
最后,改变过盈量的数值,取其为δ=3.2%,则其模拟结果如图9所示。很明显,采用过盈配合的清管方式,相比于以上两种清管方式,能够达到最优的除垢效果,在理想的模拟环境下,可以将污垢完全在管壁剥离,并且污垢不会残留在管道内部。
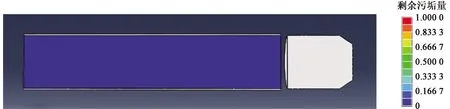
图9 过盈配合情况下的清管效果Fig.9 Pigging effect of interference fit
4 结 论
(1)得到的管道与清管器之间的相互作用力与相对过盈量的函数关系表明平面应力模型和空间轴对称模型与数值结果非常接近,符合工程实际。
(2)基于推动力和摩擦力的平衡方程,给出了工程中一种求解过盈量的方法。根据推力与相对过盈量之间的函数关系,验证了工程中常用管道-清管器结构的过盈量都满足工程设计需求,即在1%~10%之内。
(3)基于确定的过盈量计算的理论模型,针对具有不同过盈量的泡沫清管器结构,对其清除油蜡混合物的过程进行模拟的结果验证,即必须合理选择过盈量,才能得到最佳的除垢效果。
