含外表面轴向裂纹管道评估模型预测精度统计推断

2021-05-25郭凌云

中国石油大学学报（自然科学版） 2021年2期

郭凌云, 周晶

(1.大连理工大学海岸与近海工程国家重点实验室,辽宁大连 116024; 2.大连理工大学建设工程学部土木工程学院工程抗震研究所,辽宁大连 116024)

近年来随着既有管道的老化,管道失效时有发生,严重地影响了油气等物质的正常运输[1-2]。为了更好地对管道进行运营管理,研究管道的失效状态,确定管道的临界失效内压至关重要。目前,中国关于管道失效模型的研究主要集中在腐蚀管道上[3],针对含裂纹管道的失效研究则比较匮乏。有关含裂纹管道的评估主要借鉴锅炉等压力容器的失效规范,并且适用范围有限。因此研究含裂纹管道的失效机制对于完善我国管道基础规范意义重大。关于含裂纹管道失效,一些研究基于工程经验、实验和有限元模拟进行拟合,并形成一些模型,如CorLAS模型[4]、Battelle模型[5]和SINTAP规范[6]等。大多数模型虽然便于操作,但忽略了预测过程的不确定,故而产生极大隐患。因此,应对预测模型的误差分布进行研究,但有关裂纹管道误差统计的分析尚处于探索阶段,研究成果匮乏、分析片面、研究深度有限,如Mahmoud等[7]主要停留在采用均值和变异系数等统计学参数对模型误差进行分析上;Cosham等[8]仅对比了NG-18模型和BS7910:2005规范管道失效内压的散点分布等。针对该问题,利用极大似然估计法(MLE)[9]进行参数拟合,结合Kolmogorov-Smirnov检验(K-S检验)[10]对预测精度分布规律进行拟合优度测量,从而选择满足检验的最优拟合分布。笔者基于机器学习和统计学相关理论对内压荷载下含外表面轴向裂纹管道的评价模型预测精度进行分析。

1 轴向外裂纹管道评估标准

利用7种常用的裂纹管道计算模型进行分析,包括:Battelle、CorLAS、API RP 579、SINTAP/FITNET FFS、BS7910:2019、R6和GB/T 19624-2019在用含缺陷压力容器安全评定[4-6,11-18]。除Battelle和CorLAS模型外,其余模型均采用FAD图进行评价,如图1所示。当点B位于蓝线以内时,结构安全;位于蓝线以外时,结构失效;位于曲线上时,结构处于临界状态。直线OB与失效应力曲线的交点A为管道预测失效点,据此可得临界失效压力。值得注意的是,除Battelle模型将裂纹剖面简化为矩形截面进行计算外,其他规范中一律简化为半椭圆状裂纹剖面计算,简化剖面的深度和长度分别为裂纹剖面的最大深度和长度。

Lr=σref/σy,

(1)

Kr=KI/Kmat.

(2)

图1 裂纹管道失效评估Fig.1 Failure assessment diagram of crack-containing pipeline

1.1 Battelle 模型

Battelle模型是美国Battelle实验室于20世纪60、70年代开发的用于预测仅承受内压的含有轴向表面裂纹管道的爆破压力半经验模型,又称ln-sec模型或NG-18方程[4]。该模型基于流动应力和断裂韧性两个破坏准则确定爆破压力,表示为

(3)

其中

σf=σy+68.95,

式中,a为裂纹深度,mm;c为裂纹半长度,mm;t为管壁厚度,mm;D为管外直径,mm;σf为管道材料流应力,MPa;p0为管道预测极限内压,MPa;M为Folias鼓胀系数;E为弹性模量,MPa;Cv为夏比冲击能,J;Ac为夏比冲击试样的净横截面积(全尺寸试样截面面积为80 mm2,2/3尺寸试样截面面积为53.55 mm2),mm2。

1.2 CorLAS模型

CorLAS模型为CC技术公司开发的评估管道完整性的常用工具[5]。该模型与Battelle模型类似,考虑两个独立的失效准则:流动应力准则和断裂韧性准则。爆破压力计算式为

(4)

其中

σcrit=min{σf,σ1},σf=(σy+σu)/2.

式中,σcrit为许用应力,MPa;σ1为基于韧性准则的裂纹局部破坏应力,MPa。

σ1可通过求解J=Jc获得,其中Jc=Cv/Ac。式中,J为抗断裂性,计算过程详见文献[4]附录A,kJ/m2;Jc为J积分的临界积分,表示断裂韧性,kJ/m2。

1.3 SINTAP/FITNET FFS

SINTAP是欧洲共同体基于断裂力学针对缺陷结构所编制的评价规范[6],并由多所研究机构发展为FITNET FFS商定评价程序,广泛用于各类金属部件的评估中[11]。在SINTAP评价规范中,根据所提供的材料数据的详尽程度分7个等级,即Level 0～Level6。主要利用Level 1对压力裂纹管道进行评估,该等级分为Level 1A和Level 1B。

当管材有屈服平台时,采用Level 1A评估准则进行研究,表示为

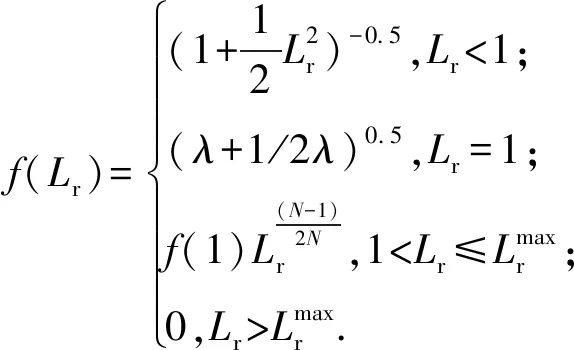
(5)

其中λ=1+(EΔε)/σy,Δε=0.037 5(1-σy/1 000);N=0.3(1-σy/σu)。

当管材无屈服平台时,采用Level 1B进行评估,表示为

(6)

其中

μ=min[0.001(E/σ0.2);0.6].

式中,σ0.2为无屈服平台金属材料的屈服强度,MPa。

本规范的荷载比Lr计算式为

Lr=pm/(1-ζ)σy.

(7)

其中

ζ=ac/[t(c+t)].

式中,pm为薄膜应力,MPa,适用于a/t≤0.8。

1.4 BS7910:2019

BS7910:2019是英国标准委员会于2019年发表的金属结构缺陷评估标准,记为BS7910[14]。该标准分3个评价等级,即Option 1～Option 3。采用Option1等级进行评估,Option 1的计算过程与SINTAP的Level 1一致,分为材料有无屈服平台情况,见式(5)和式(6)。其Lr和Kr的表达式为式(1)和式(2)。σref和KI的计算过程和应用范围详见该规范附件P和附件M。Kmat计算式为

(8)

1.5 R6

R6是由英国中央电力局发布的评估金属缺陷结构方法,分3级评价,即Option1～Option3[15]。其中Option 2A是Option 2的近似,是常用的评估选项,因此采用Option 2A进行研究。Option 2A的表示与SINTAP的Level 1和BS7910:2019的Option1相同,如式(5)和(6)所示。

Lr的表达式为

Lr=p/pL.

(9)

塑性破坏极限内压pL有全局解和局部解两种形式。其中全局解是轴向方向不稳定而造成的全面爆破,依赖于屈服准则,可用Tresca和Von Mises准则进行研究,结果记为R6-1和R6-2;局部解是壁厚方向上的不稳定而导致的局部塌陷,结果记为R6-3,具体计算见文献[4]附录B。

Kr计算见式(2),其中KI的计算详见该规范IV.3.4.3节。Kmat基于Rolfe-Novak-Barsom模型[16],计算式为

(10)

1.6 API RP 579

API RP 579是由美国机械工程师协会与美国石油协会共同研究的缺陷承压设备适用性评价规范[17],记为API,包含3个等级,即Level 1～Level 3。利用Level 2进行分析,表示为

(11)

Lr和Kr可用式(1)和(2)计算。σref和KI的计算过程及适用范围详见该规范9B.5.10和9C.5.10节,其中KI与R6计算一致。Kmat的计算与R6规范中的Kmat规定一致,用式(10)进行求解。

1.7 GB/T 19624-2019 在用含缺陷压力容器安全评定

Lr和Kr的计算见式(1)和式(2)。σref的计算过程与BS7910的σref一致,见该规范附录A.4。但该规范并未对含外表面裂纹管道的KI进行规定,由于规范中内表面裂纹管道的KI计算与规范BS7910计算一致,故本文中参考BS7910的KI计算对其分析。此外,Kmat与BS7910的Kmat计算一致。

2 数据实验

分析含裂纹管道预测爆破内压,收集含裂纹的管道爆破数据,且满足要求:①管道径厚比为D/t>22;②缺陷类型为外表面轴向裂纹;③裂纹剖面为半椭圆或矩形剖面,且裂纹深度小于壁厚的0.8倍;④所受荷载仅为内部压力。

根据以上条件,从文献中筛选出爆破实验数据89组[19-27],参数范围见表1。

表1 实验数据的参数范围Table 1 Parameters range of test data

需要注意,由于各规范适用范围不同,因此并非所有规范都能计算出每组实验的预测压力。其中Battelle,SINTAP,BS7910和GB模型可预测89组数据;CorLAS可预测84组数据,而R6和API可预测74组数据。

3 统计推断

基于89组数据计算含裂纹管道失效压力p0,并将其归一化(p0/pC),获得预测精度PA。基于极大似然估计法(MLE)和Kolmogorov-Smirno检验(K-S检验)对PA分布进行参数估计和拟合优度评定。

3.1 假设分布及其参数确定

采用Melchers等[28]提出的常用误差分布模型对PA的分布进行假设,即正态、对数正态、Gumbel、Frechet和Weibull分布。采用MLE[9]对其参数进行估计,似然函数为

(12)

式中,L(θ,x)为似然函数;xi为数据样本;n为样本容量。

3.2 拟合优度评定

拟合优度评定是机器学习中确定数据分布特征的重要组成。结合数据特征,采用Kolmogorov-Smirno检验(K-S检验)进行拟合优度分析[10]。该检验是基于累积频率Fn(x)和假设分布函数F(x)的偏差D判断样本是否服从假设分布,表示为

(13)

式中,Fn(x)为观测累积分布对应值;F(x)为假设分布对应值;D为累积分布与假设分布偏差。

获得D值后,该检验根据Kolmogorov表计算对应P。当P大于置信度α(取0.05)时,接收H0,即从统计意义上认为,样本服从假设分布,反之亦然。因此最优分布需满足P>α,且偏差D最小。

4 分析与讨论

图2和表2分别为不同模型的PA分布情况和不同假设分布的拟合优度。基于图2和表2的数据拟合情况,确定不同规范的PA最优拟合分布(P>0.05,D最大),见表3。

基于表3不同模型的PA分布,绘制其概率分布,见图3。利用PA大于1、小于0.5和介于0.5与1之间的概率分别代表预测结果危险性、保守性和集中性,并进行计算见表4。综合以上计算结果,按图3的PA分布从右到左依次分析模型的预测性能。

图2 不同模型的PA分布Fig.2 Distribution of PA for different models

CorLAS模型的PA服从参数为0.935和0.287的正态分布,并具有如下性质:①直方图具有多峰性;②所服从分布的峰值出现在1附近,且高度最低,即离散度最高;③危险性对应概率为40.02%,远高于其他规范。这些特性说明该组规范预测虽然正确性较高,但预测稳定性能低,预测结果最为危险。因此采用此规范进行预测时,应慎重使用其预测结果。

Battelle模型的PA用参数为0.848和0.208的Gumble分布进行描述。相较于其他规范,该规范的预测精度有以下特点:①直方图呈现多峰性;②所服从的分布峰值位置偏左,且高度低;③危险性概率为12.53%,保守性的概率为17.21%。这些特点均反映了该规范的预测性能不稳定,危险性和保守性均偏高。因此该规范所计算的结果也应谨慎使用。

表2不同模型的PA的假设分布拟合优度Table 2 Goodness-of-fit of PA hypothetical distribution for different models

表3 不同模型PA的最优拟合分布Table 3 Best-fit distribution of PA for different models

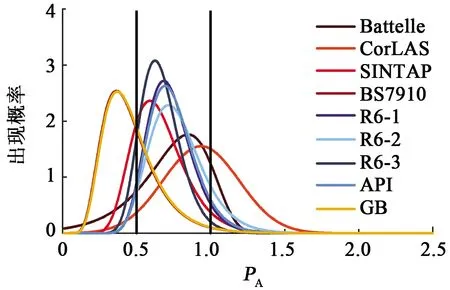
图3 不同模型PA的分布概率密度Fig.3 Probability density diagram of PA for different models

R6-1、R6-2、R6-3和API规范预测性质相近,都具有以下特点:①直方图为单峰分布,预测结果稳定;②服从对数正态分布,且峰值位置相差不大,在0.7附近;③集中性,介于0.5到1.0之间的概率超过80%。因此该组规范的预测性质明显优于前两组。分析该组规范彼此间差异,基于预测性能相差不大时,推荐危险性较低的预测模型的原则,结合峰值高度、危险性、保守性可以得出:①R6-3的危险性为1.72%,非常理想,但保守性偏高,为9.79%,总体预测效果最优;②R6-1和API的危险性偏高,约6%,但稳定性和保守性均衡,故预测效果次之;③R6-2危险性相对最高,为11.99%,但保守性和稳定性均衡,故组内最差。因此使用该组规范进行预测时,推荐顺序为R6-3、R6-1(或API)和R6-2。

表4 不同模型PA的预测性能Table 4 Prediction performance of PA for different models

SINTAP规范的PA服从参数为-0.451和0.275的对数正态分布。其预测特点有:①直方图为单峰,预测稳定性高;②峰值出现位置偏小,约为0.6;③保守性概率偏高,为18.99%,危险性概率较低,为5.04%。相较其他规范,该模型的预测稳定性较好,危险性也较低,但保守性偏高。因此在预测管道失效内压时,该规范的优先级低于第三组规范。

BS7910和GB规范的PA预测分布几乎重合,呈对数正态分布,其分布性质有:①直方图为明显单峰;②分布的峰值位置出现在0.4附近;③保守性概率约为65%,危险性概率约为1.6%。以上特性反映:该组规范预测相对稳定,但过于保守,可能会造成材料一定程度上的浪费。因此建议该组规范适用于安全系数要求比较高的工况。

观察第三组规范和第五组规范,发现: BS7910和GB规范的荷载比和断裂比的算法相同,R6-1、R6-2、R6-3和API规范中计算断裂比的方法相同。该现象表明:当断裂比和荷载比的计算方法均相同时,预测分布基本重合,反映上述模型中的两种FAD曲线无明显区别。当仅有断裂比的计算方法相同时,预测值的分布形状及位置会表现出一定的相似之处,即断裂比对于预测模型的预测性能有较大影响。综上所述,对采用FAD图评价的模型来说,两种FAD曲线彼此间无明显差异,受断裂比的影响较大。