超声临界折射纵波测量应力的温度影响
2021-05-25李玉坤于文广李玉星陶建中
李玉坤, 于文广, 李玉星, 张 玉, 陶建中, 程 磊
(1.中国石油大学(华东)储运与建筑工程学院,山东青岛 266580; 2.国家石油天然气管网集团有限公司油气 调控中心,北京 100020; 3.国家管网集团西部管道有限责任公司,新疆乌鲁木齐 830000)
工程结构工作应力的无损检测对保障工程结构的安全具有重要意义[1]。工程结构内部应力较大带来诸多不利影响[2-3],包括翘曲变形[4]、应力腐蚀开裂[5]、过早疲劳破坏[6],在工程结构的服役阶段必须高度重视工作应力的测量。超声波法是当前无损检测工程结构工作应力的有效方法。ROSSINI等[7]认为超声波法具有高分辨率、高渗透力和对人体无伤害的特点,是工作应力无损检测发展方向上最有前途的技术之一。超声波法测量应力基于声弹性理论,通过超声波传播速度的改变量计算被测工程结构的应力[8]。超声波法测量应力具有无损、快速、可适用范围广等特点,但也有着影响因素多的缺点,其中温度、耦合状态、被测点的粗糙度等因素直接影响了超声波法测量应力的精度和现场可应用性[7]。Fraga等[9]研究指出在众多影响超声波测量应力因素中,温度影响程度最显著。Salama等[10-11]、Chern等[12]、Heyman等[13]及Kobori等[14]测量了超声波波速随温度的变化量,定义了热-声系数,明确了该系数随应力变化规律。Weaver等[15]研究指出超声波传播速度的温度依赖性表现为超声信号的扩散或压缩。Nikitina等[16]利用超声波法测量管道双轴应力,发现超声纵波和横波速度对温度依赖性之间的差异,给出温度影响程度。贾大伟等进一步得到超声波波速与温度变化呈线性关系[17]。Lobkis等[18]指出温度和应力对超声波传播的影响差异可以使两种效应分离,为温度对超声波测量应力的修正提出理论支持。Dhawan[19]利用导热系数和高阶弹性常数,用梅森理论(Mason theoretical)方法确定了单晶GaAs-NW的超声衰减和热弛豫时间随直径和表面粗糙度函数。目前已有较多超声应力测量温度依赖性的研究成果,但缺乏超声应力测量的温度依赖性的机制解释,多采用试验数据拟合温度影响公式,缺少理论与试验的相互验证,影响了工程推广应用。笔者从超声LCR波在被测结构中传播规律入手,研究超声LCR波测量应力公式中声弹性系数和零应力下飞行时间与温度的关系,分析温度影响超声LCR波测量应力的机制,推导超声LCR波测量应力的温度补偿公式。设计可消除声楔块和耦合剂影响的一发两收超声换能器,开展不同温度下LCR波零应力飞行时间测量试验。
1 理 论
1.1 声弹性理论
如图1所示,超声LCR波是一种在材料内部特定深度传播且平行于材料表面的纵波。EGLE和BRAY[20-23]已经通过试验证明:相比于其他形态的超声波,超声LCR波对应力有更高的敏感性。第一临界角可表示为

(1)
式中,v1和v2分别为波在介质1和介质2中的传播速度,m/s;θLCR、θS和θL分别为第一临界角、折射波剪切角和纵波折射角,(°)。

图1 临界折射纵波生成示意图Fig.1 Generation of critical refraction longitudinal wave
在材料弹性限度内,基于应力与声飞行时间成线性关系,用超声LCR波法测量应力;当超声LCR波沿着应力方向传播,传播速度与应力关系[20]为
(2)
式中,v11为平行于加载方向的波传播速度,m/s;ρ0为材料零应力下的初始密度,kg/m3;λ,μ为二阶弹性模量,Pa;l,m,n为三阶弹性模量,Pa;σ11为平行于加载方向上应力,Pa;k0为材料的体积弹性模量,Pa。
材料的体积弹性模量可表示为

(3)
式中,E为弹性模量,Pa;ν为泊松比。
对于处于零应力状态下的被测材料,式(1)可表示为
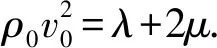
(4)
式中,v0为超声LCR波在零应力试件内的飞行速度,m/s。
将式(4)代入式(2),消去密度,得

(5)
将式(3)代入式(5)中,得

(6)
化简得

(7)
KL定义为临界折射纵波的声弹性系数,其表达式为

(8)
对式(7)取微分,得

(9)
超声LCR波传播速度变化很小,近似取v11=v0,式(9)可化简为
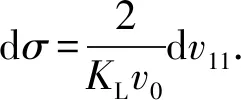
(10)

(11)
式中,t和t0分别为有应力和零应力介质中超声LCR波飞行时间,s。
由式(11)可知,超声LCR波的声弹性系数KL和超声LCR波在零应力试件中的飞行时间t0对测量应力变化量Δσ有直接影响,而温度变化直接影响着这两个量的数值,得到这两个量在不同温度下的数值是保证超声波测量应力准确性的关键。因此探讨温度对超声波法测量应力的影响机制,应进一步探究温度对KL和t0的影响规律。
1.2 温度影响机制
1.2.1 温度对超声LCR波声弹性系数KL的影响
临界折射纵波声弹性系数KL由二阶和三阶弹性模量表示,对其进行推导简化。根据弹性力学可知,材料的二阶和三阶弹性系数可表示为
(12)
将式(12)代入KL中,进行连续推导得
(13)
超声LCR波的声弹性系数KL是材料弹性模量E和泊松比ν的函数,声弹性系数KL随弹性模量E增大而减小,随泊松比ν增大而增大。常温范围内(-10 ~ 40 ℃),金属材料的弹性模量和泊松比受温度影响极小,基本保持不变[24]。因此在常温范围内,超声LCR波的声弹性系数KL可以视作常数,不受温度影响。
1.2.2 温度对零应力下LCR波飞行时间影响
零应力(free-stress)条件下超声LCR波在试件中飞行时间t0同样受温度影响,t0T记为某温度下超声LCR波在零应力试件的飞行时间。t0T可通过变温试验条件下超声LCR波在零应力试件中的波速v0,T和在超声波传播声程L0T表达。
将式(4)中各阶弹性系数用弹性模量和泊松比表达得

(14)
式中,ρT为任意温度下密度,kg/m3;v0T为任意温度零应力状态下超声波波速,m/s;L0T为超声波传播距离,m。
ρT用体积膨胀系数和给定温度下的密度ρ0表示为

(15)
式中,αV为体积膨胀系数,℃-1;ΔT为温度变化量,℃。
故任意温度零应力状态下的超声波波速可表达为
(16)
联立式(14)与式(150得任意温度下零应力状态超声波飞行时间为
(17)
由式(17)可知,任意温度下超声LCR波在零应力试件的飞行时间t0T与参数L0T、E、ν、αV、ΔT、ρ0有关。在常温范围 (-10 ~ 40 ℃) 内,E、ν、αV、ρ0变化十分微小,视作常数。因此t0T对温度的依赖性归于L0T对温度的依赖性和温度变化量ΔT。在材料热胀冷缩效应下,温度影响超声换能器的尺寸,有效声程L0T将发生变化。
1.2.3 超声LCR波测量应力温度补偿公式
超声LCR波的声弹性系数KL和超声LCR波在零应力试件中的飞行时间t0对测量应力变化量Δσ有直接影响。声弹性系数KL是材料弹性模量E和泊松比ν的函数。常温范围内(-10 ~ 40 ℃),金属材料的弹性模量和泊松比受温度影响极小,基本保持不变。因此在常温范围内,超声LCR波的声弹性系数KL可以视作常数,不受温度影响。超声波测量应力温度补偿公式为

(18)
2 不同温度下零应力LCR波飞行时间测量试验
2.1 超声LCR波应力测量试验平台
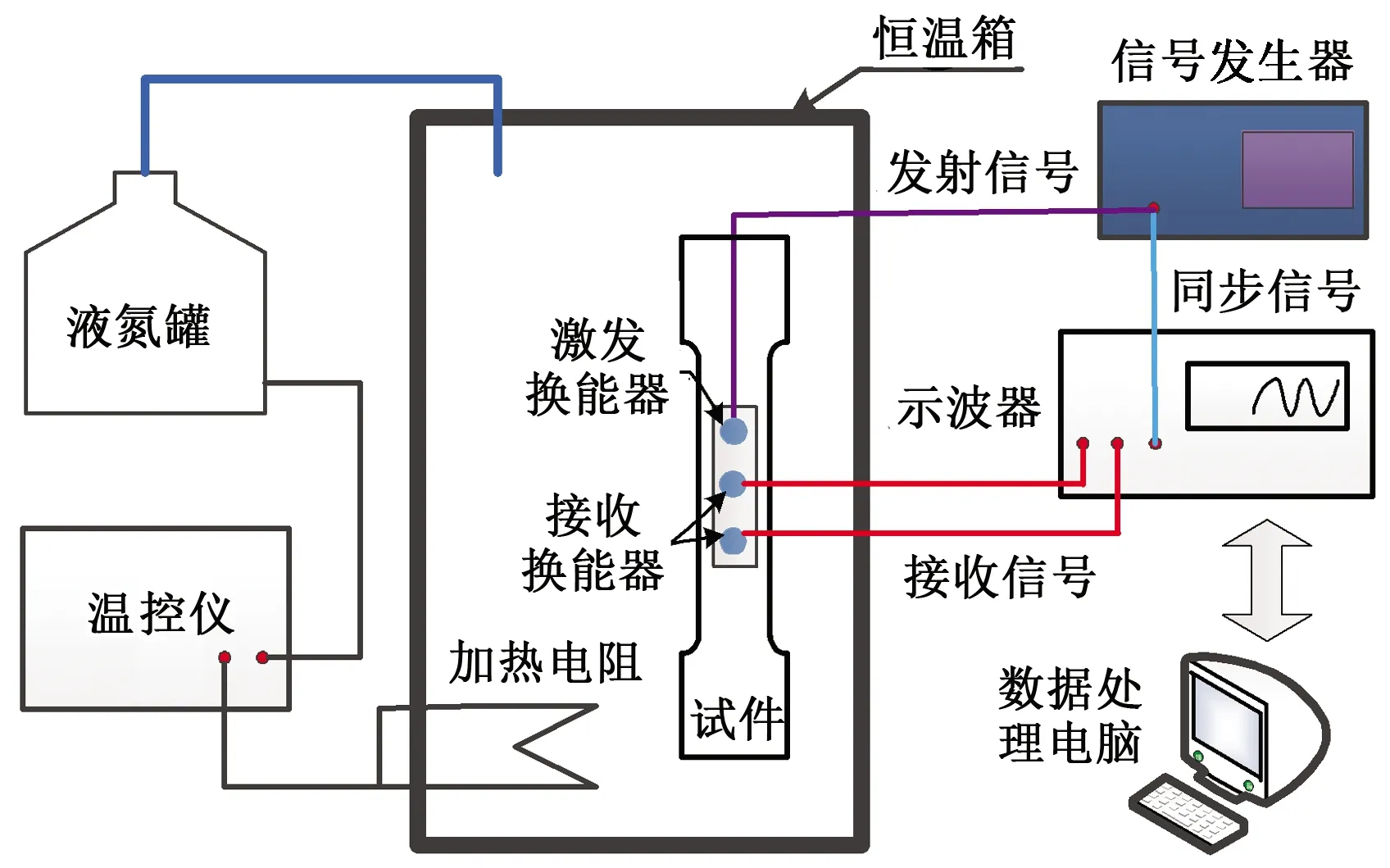
图2 超声LCR波应力测量试验平台Fig.2 Experimental platform for stress measurement of ultrasonic LCR wave
如图2所示,超声LCR波应力测量试验平台包含超声测量系统和控温系统。超声测量系统包含数据处理电脑、超声波信号发生器(奥利巴斯5072PR)、数字示波器(GWINSTEK GOS-2204A)、超声换能器(一发两收)、A36钢试件。控温系统包含控温器、电阻丝加热器、液氮瓶及管路、恒温箱。控温系统的温度调节范围为-50~80 ℃,精度为0.2 ℃。
超声测量系统工作原理为信号发生器激发高压脉冲信号,其中一束作为发射信号传送到超声发射换能器,另外一束作为同步信号传送到数字示波器;超声发射换能器将接收到的高压脉冲信号转换为超声波信号(5 MHz),超声波信号在被测介质中传播,超声接收换能器接收超声波信号,将超声波信号转换为电压信号;接收信号与同步信号都传递给数字示波器,数字示波器将采集的信号传递给电脑;电脑对超声接收信号和同步信号进行对比处理,得到超声波在介质中飞行时间。
如图3所示,本试验所用试件均从同一块A36钢板中切割得到。试件加工完成后进行退火处理(加热到450 ℃保温2 h,然后再随炉冷却),以消除初始应力。为了去除氧化物和减少孔隙度,试验前用质量分数为5%的稀盐酸对试件进行化学表面处理。

图3 试件Fig.3 Specimen
如图4所示,为解决超声换能器声楔块和耦合剂对准确测量超声LCR波飞行时间的影响,采用一发两收超声换能器。
2.2 一发两收超声换能器温度影响
为消除超声换能器声楔块和耦合剂对测量超声LCR波飞行时间的影响,设计制作了专用的一发两收超声换能器。超声LCR波的传播过程:发射换能器—声楔块—耦合剂—A36钢—耦合剂—声楔块—接收换能器。接收换能器1和接收换能器2所测的超声LCR波飞行时间为

(19)
式中,t1和t2分别为接收换能器1和接收换能器2测量超声波飞行时间,s;tC为超声波在耦合剂中的飞行时间(假设耦合剂均匀分布),s;tLg为超声波在声楔块中传播Lg路程的时间,s;tL1和tL2分别为超声LCR波在A36钢中传播L1路程和L2路程的时间,s。
t2和t1的差值为
t2-t1=(tLg+tC+tL1+tL2+tC+tLg)-(tLg+tC+tL1+tC+
tLg)=tL2.
(20)
t2与t1的差值为超声LCR波在A36钢中传播L2路程的时间。一发一收超声换能器所测超声波飞行时间为超声波在声楔块、耦合剂、A36钢中飞行时间总和。采用一发两收超声换能器,两个接收换能器所测时间差值为超声波在A36钢中传播L2路程的时间。由此可知,采用一发两收超声换能器,可有效去除声楔块和耦合剂的影响,准确得到超声波在A36钢中的飞行时间。

图4 一发两收超声换能器示意图和实物图Fig.4 Schematic and physical diagrams of one-send and two-receiver ultrasonic transducer
对于一发两收超声换能器,温度影响主要有:①温度变化对超声LCR波在A36钢中传播速度的影响;②温度变化对传播声程L2的影响(超声换能器热胀冷缩)。在式(18)中,L2代替L0。
温度变化时,声楔块热胀冷缩,引起声楔块覆盖的被测工件中的声程L2变化,从而引发有效声程的变化。因此当温度变化ΔT时,声程LT为
LT=L2(1+αlΔT).
(21)
式中,αl为声楔块的热膨胀系数。
温度升高使得声程增大,引起声时差增大,即对应力测量结果产生误差。
任意温度下零应力状态超声波飞行时间为

(22)
2.3 变温试验测量温度对LCR波飞行时间影响

图5 零应力变温试验装置Fig.5 Zero stress variable temperature experimental device
如图5所示,利用搭建的超声LCR波应力测量试验平台开展试验,将一发两收超声换能器和A36钢试件放置于恒温箱中,耦合剂采用硅油。利用控温系统调节恒温箱内温度,温度范围为-4.2~28.2 ℃。每调节一次温度,待恒温箱内温度稳定后,利用超声测量系统保存两个接收换能器接收到的超声波信息。试验结束后对数据进行分析处理。
试验中采用一发两收超声换能器,图4是换能器的照片,其中L2=15 mm,超声频率为5 MHz,换能器和被测介质的倾斜角为28°。
3 试验结果与讨论
3.1 试验结果
利用超声LCR波应力测量试验平台开展变温试验,温度范围为-5~30 ℃。测量超声LCR波在A36钢试件中的飞行时间。对超声波数据进行处理,提取接收换能器1和接收换能器2的超声波信号,计算得到超声LCR波在A36钢中L2声程下的飞行时间Δt。根据测量数据,作出超声波飞行时间随温度变化的曲线,见图6。

图6 超声波飞行时间随温度变化曲线Fig.6 Change curve of ultrasonic flight time with temperature
如图6所示,接收换能器1测量的超声波飞行时间t1与温度T呈线性关系,t1随温度T升高而线性增加,拟合公式为t1=3.922T+6 983.4。说明温度每升高1 ℃,超声波飞行时间t1将增加3.922 ns。t2与温度T同样呈线性关系,t2随温度T升高而线性增加,拟合公式为t2=4.356 7T+9 668.1。说明温度每升高1 ℃,t2将增加4.356 7 ns。Δt与温度T也呈线性关系,Δt随T升高而线性增加,拟合公式为Δt=0.434 6T+2 684.7。说明温度每升高1 ℃,超声波飞行时间Δt将增加0.434 6 ns。
3.2 讨 论
为分析超声波飞行时间的温度依赖性,定义超声波各参数受温度影响程度为温度系数Z,将t1、t2和Δt传播速度v的温度系数整理,得到Zt1=3.922 ns/℃,Zt2=3.922 ns/℃,ZΔt=3.922 ns/℃。
Zt1 根据试验结果验证式(17)。温度范围为-5 ~ 30 ℃,A36钢弹性模量E和泊松比ν可视为常数。式(17)中各参数取值为:弹性模量E=2.0×1011Pa,泊松比ν=0.26,初始密度ρ0=7 850 kg/m3,体积膨胀系数αV=3.6×10-5℃,热膨胀系数αl=1.8×10-4℃,声程L2=0.015 m。 图7 公式计算和试验测量曲线Fig.7 Formula calculation and experimental measurement curve 将A36钢各参数代入式(17)中,温度变化量取-5 ~ 30 ℃,计算得到不同温度下超声LCR波在A36钢中飞行时间t0T。图7为公式计算和试验测量曲线。由图7可知,由式(17)计算得到的超声波在A36钢中L2声程下飞行时间t0T与温度T关系为t0T=0.435T+2 686.6;通过试验测量得到的超声波在A36钢中L2声程下飞行时间Δt与温度T关系为Δt=0.434 6T+2 684.7。 对比图7中两条曲线可知,公式计算得到的曲线公式和试验测量曲线公式呈现出很好的一致性。试验和计算得到的温度系数(关系曲线的斜率)相差小于0.1%。试验结果充分验证了理论推导公式的精度。 (1)声弹性系数是弹性模量和泊松比的函数,随弹性模量增大而减小,随泊松比增大而增大;在常温范围内(-5~40 ℃),金属材料弹性模量和泊松比基本保持不变,声弹性系数可以视作常数。在常温范围内,零应力下飞行时间与声程(传播距离)成正比,与温度变化量成反比。在材料热胀冷缩效应下,温度影响超声换能器尺寸,有效声程进而发生变化。 (2)设计的一发两收超声换能器有效消除了声楔块和耦合剂的影响,显著降低温度影响水平。一发两收超声换能器的两个接收换能器所测时间差值为超声LCR波单纯在A36钢中的飞行时间,去除声楔块和耦合剂的影响,准确得到超声波在A36钢中的飞行时间。设计的一发两收超声换能器对温度的依赖性仅为一发一收换能器的10%。 (3)推导了超声波测量应力的温度补偿公式。试验测量和理论计算得到的飞行时间与温度关系曲线表现出很好的一致性,两种方法得到的温度系数(关系曲线的斜率)相差小于0.1%。试验结果充分验证了补偿公式的准确性。
4 结 论
