Taylor定理教学探究

周艺璇

(四川民族学院 理工学院，四川 康定 626000)

在高等数学中，Taylor定理是最重要的定理之一，本质上是用相对简单的多项式函数逼近较复杂的一般函数。在求极限、求导数、求积分、不等式证明、函数性态分析、判定级数敛散性以及近似计算等方面都有着重要应用[1-4]。同时，它也是数值分析、常微分方程、最优化理论等数学分支的重要理论基础。Taylor定理高度的抽象性、严密的逻辑性往往使得初学者望而生畏。为了帮助学生理解和掌握Taylor定理，适当演绎和证明Taylor定理是非常必要的。

1 多项式逼近函数问题

由微分在近似计算中的应用可知，若f(x)在x0处可导，则

f(x)=f(x0)+f(1)(x0)(x-x0)+o(x-x0)。

其中f(x0)+f(1)(x0)(x-x0)可以看作一次多项式P1(x)，从而有f(x)=P1(x)+o(x-x0)。若忽略高阶无穷小，则可以用来P1(x)逼近f(x)。谢惠民教授在《数学分析习题课讲义》[5]中以例题6.1.3为例，严格证明了：与任意线性函数相比，P1(x)总能找到x0的某个邻域U(x0)，使之与f(x)的差值更小。因此，在一次多项式中，用P1(x)来逼近f(x)是最优的。这也是高等数学教材选择用微分近似公式引入的原因。

事实上，多项式的优势是很明显的，它只涉及加法、乘法和减法三种运算，并且求导、求值都很方便。因此，如何利用多项式来描述一个给定的函数就是我们接下来逼近问题的重点。

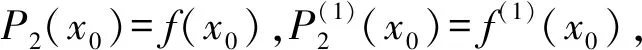
通过对P1(x)与P2(x)进行对比分析，我们发现为了进一步提高精度，n次多项式Pn(x)首先得具有与P1(x)和P2(x)类似的构造，其次它的各阶导数都存在。于是假设f(x)在x0处n阶可导，是否存在n次多项式Pn(x)=a0+a1(x-x0)+a2(x-x0)2+…+an(x-x0)n，使得f(x)=Pn(x)+o((x-x0)n)?下面我们说明Pn(x)的存在性和唯一性。

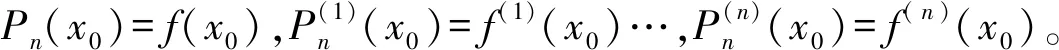
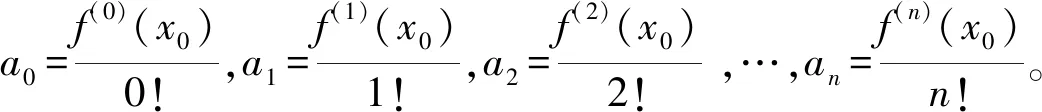
为了验证求得Pn(x)的逼近f(x)的效果，选择验证Pn(x)逼近f(x)所产生的误差也就是f(x)-Pn(x)是否是o((x-x0)n)是最为直接且方便的方法。如果是，得到的Pn(x)就是f(x)的很好的一个逼近。

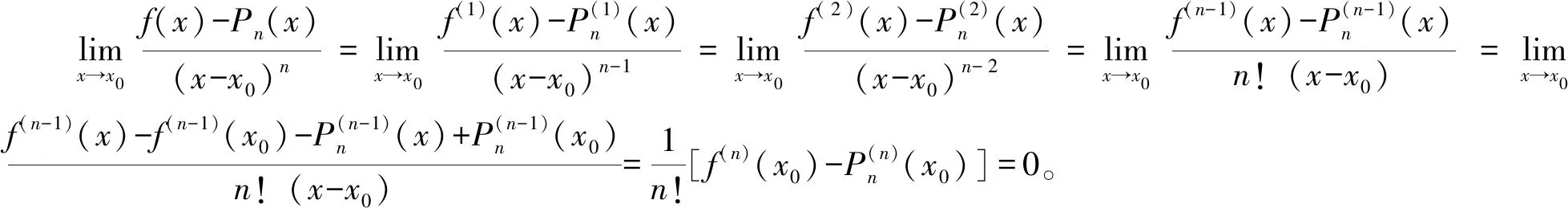
至此，我们已经说明高次多项式可以很好的逼近一般函数。通过这样一个详细的推演，不仅能使学生更加清晰Taylor定理的整个证明过程，而且还能激发学生进一步深挖课本知识的兴趣。从实际教学过程来看，利用直觉发现问题、提出猜想在解决问题的过程中起着关键性作用。而形式推导则是验证猜想的重要方法。这种处理方法，在能力提升方面，既可以培养学生的创造性思维，也可以锻炼学生的逻辑推演能力，进一步地能更清楚的认识几个微分中值定理之间的内在联系，从而构建起相关理论的框架，为之后专业课程的学习提供扎实的基础。在知识讲授上，既能巩固微分中值定理，又能比较自然的引出Taylor公式，从而使得学生更易于接受并掌握Taylor定理。从实际教学效果来看，确实取得了满意的效果。

2 Taylor定理

把上述结论上升为定理，即第1种形式的Taylor定理。

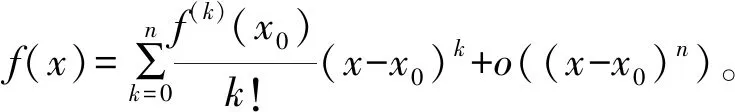
从某种意义上讲，余项Rn(x)=o((x-x0)n)也是一个误差。即Pn(x)逼近f(x)所产生的误差。通常Taylor公式被用于做近似计算，但是带Peano余项的Taylor公式在实际应用中是有一定缺陷的。具体在于：

(1)精确度不够。它只给出了余项的定性描述，说明余项是高阶无穷小。

(2)误差无法估计。具体的阶数没有体现，从而不能对误差进行定量分析。

(3)适用范围较小。带Peano余项的Taylor公式若要和f(x)划等号，前提必须是x与x0靠得比较近。

那自然就会产生下面一个问题：怎么样克服Taylor公式Peano余项的缺点，而保持它的优点。即它的右端仍然是一个多项式，但误差项是可以进行定量分析的具体的表达式。另外还要扩大它的适用范围，比如，是否能将附近的范围扩大到区间上？这个区间是否可以无限？带着这些疑问，再次回顾旧知。

如果f(x)在区间[a，b]上可导，并且假设x0∈[a，b]，x=x0+Δx∈[a，b]，则根据Lagrange中值定理有f(x)=f(x0)+f(1)(ξ)(x-x0)，其中ξ介于x0与x之间。

于是猜测：如果f(x)在区间[a，b]上二阶可导，那么f(x)的表达式会不会在形式上有类似的推广。即f(x)=f(x0)+f(1)(x0)(x-x0)+f(2)(ξ)(x-x0)2。

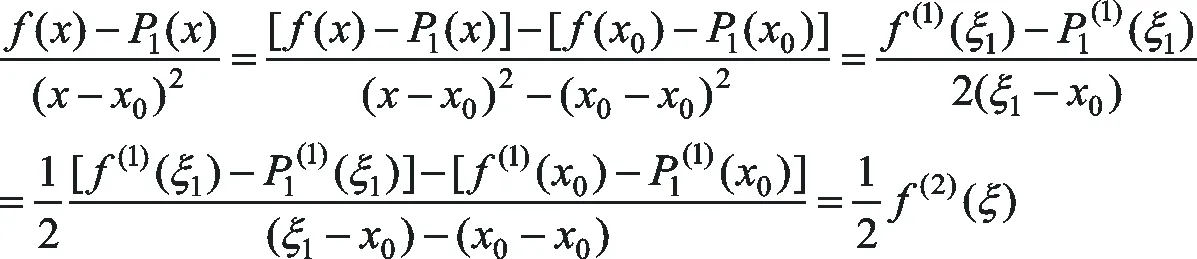
于是我们修正猜测，并总结出：如果f(x)在区间[a，b]上二阶可导，则

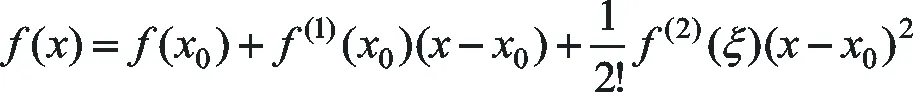
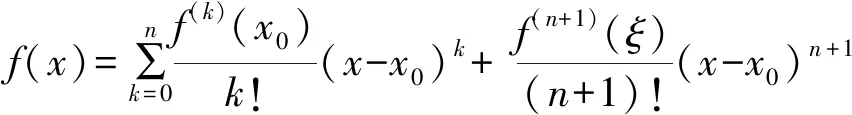
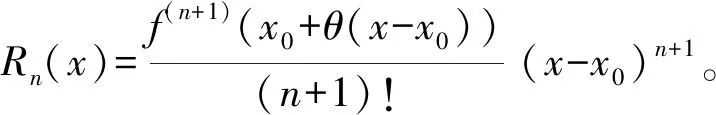
3 两种形式的Taylor定理的比较

(1)条件不同。Peano要求函数在x0处n阶可导，而Lagrange要求函数在区间n+1阶可导。

(2)余项的表达式不同。Peano余项是一个高阶无穷小，而Lagrange的余项是具体的表达式，即对Lagrange余项可以进行定量分析。

(3)在带Lagrange余项的Taylor公式中，x是区间I上的任意一点，没有要求在x0附近。所以这个公式在整个区间上都是适用的。并且这个区间既可以是有限的，也可以是无限的，从而扩大了适用范围。

(4)求解方法不同。带Lagrange余项的Taylor公式是由Cauchy中值定理求得的，而带Peano余项的Taylor公式则是反复应用L’Hospital法则证明。

但从本质上讲，两者都是用多项式逼近f(x)得到的，并且都是用已知点的信息：函数值，各个阶导数值等来表示未知点。

类比是提出数学问题和猜想的一个重要途径。通过使用类比的思想方法来探究Taylor定理，能更进一步让学生加深对Taylor定理的理解与掌握。

4 举例

以y=sinx为例，从几何直观理解Taylor定理。当x0=0时，有

借助matlab数学软件，作出正弦函数sinx以及n取五次、七次、十五次时对应的多项式函数P5(x)，P7(x)，P15(x)具体的函数图像如图1。

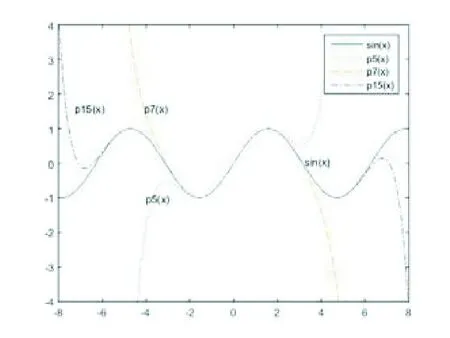
图1 当x0=0时，y=sinx与多项式函数P5(x)，P7(x)，P15(x)的图像对比

不难看出，随着次数的增加，多项式逼近sinx的效果越好，误差越小。考虑到matlab数学软件作为学习、研究和应用数学的一种工具，在后续的一些数学及工程课程的学习有着较为广泛的应用。我们可以将程序源代码告诉学生，让学生自己在课后操作，从而加深学生对于数学理论的理解，培养学生的科学计算、建模等技能。

程序源代码：

>>x=-8：0.01：8；

y1=sin(x)；

y2=x-x.^3/factorial(3)+x.^5/factorial(5)；

y3=x-x.^3/factorial(3)+x.^5/factorial(5)-x.^7/factorial(7)；

y4=x-x.^3/factorial(3)+x.^5/factorial(5)-x.^7/factorial(7)+x.^9/factorial(9)-x.^11/factorial(11)+x.^13/factorial(13)-x.^15/factorial(15)；

plot(x，y1，‘-’)

gtext(‘sin(x)’)

hold on

plot(x，y2，‘：’)

gtext(‘p5(x)’)

hold on

plot(x，y3，‘--’)

gtext(‘p7(x)’)

hold on

plot(x，y4，‘-.’)

gtext(‘p15(x)’)

axis([-8 8 -4 4])

legend(‘sin(x)’，‘p5(x)’，‘p7(x)’，‘p15(x)’)

另一方面，这也从几何直观上说明多项式函数是可以逼近一般函数的。但是前提条件是多项式函数要在开区间上n+1阶可导。由此可见，用多项式研究函数必然会给我们带来极大方便。

5 结束语

用上述方式讲授Taylor定理是比较严密的。同时，对数学中的难点，特别是证明思路和余项的比较相对全面。在讲授中，采用启发式教学方法引导学生自主探索Taylor公式，并将数学理论知识与函数图像相结合，增加了直观性。这样不仅能达到复习加深已学过知识的目的，还能提高学生学习的主观能动性，使之对学习内容产生浓厚兴趣，从而激发其智力因素，加深掌握已学知识，培养、提高逻辑思维能力和数学素养，达到满意的教学效果。