基于正交试验的高速井泵优化设计

陈建华，周晨佳，王雪，蒋小平，2，潘慧山，曹玲

(1. 江苏大学国家水泵及系统工程技术研究中心，江苏 镇江 212013； 2. 南京农业大学国家信息农业工程技术中心，江苏 南京 210095)

高速井泵结构紧凑，性能优越，维护方便.通过提高泵的转速不仅能够提升泵的水力性能，而且可以缩小泵的体积、减轻泵体重量，在节约材料的同时降低生产成本[1].近年来，高速井泵在石油、化工、航天航空等新兴产业得到广泛应用[2].

为了进一步提高高速井泵的水力性能，对叶轮的优化设计必不可少.叶轮的水力设计是一个多参数优化问题，其进出口直径、进出口宽度、叶片数、出口安放角等都对泵的性能有较大的影响[3].为了解决这一多因素问题，通常采用正交试验方法进行优化设计.通过正交表能够科学地选择其中一部分典型方案，这将大大减少试验工作量[4].李彦军等[5]选择叶轮叶片进口安放角、出口安放角、包角和叶轮外径4个因素进行正交试验方案的设计，并利用极差分析方法得到各因素对泵扬程和效率的影响程度.王洪亮等[6]以深井泵叶片数、叶轮后盖板与反导叶最底端轴向距离、进出口直径等7个因素为对象，对18组叶轮进行正交试验，得到了水力性能提高的最优模型.刘迎圆等[7]以深井离心泵为例，选取空间导叶的进口冲角、包角、叶片出口安放角和叶片数4个因素，分析了空间导叶不同结构参数对泵性能的影响规律.孙永利等[8]以捡拾辊转速、喂入口离地高度、作业速度为试验因素，以捡拾损失率、粉碎长度合格率为试验指标，进行正交试验设计，考察了各试验因素对捡拾粉碎装置工作性能的影响．

文中采用正交试验方法对100QJ10型高速井泵的叶轮进行优化设计，选取叶片出口宽度、叶轮出口直径、叶片数、叶片出口安放角、叶轮进口直径、叶轮后盖板与反导叶最底端轴向间距、叶轮出口斜切角度等7个因素，每个因素选取3个水平，共设计18组叶轮，并和同一个导叶进行装配.应用计算流体动力学软件CFX 15.0对18组叶轮进行数值模拟，分别获得其额定工况下的扬程和效率，利用极差分析法分析对水泵性能影响的主次因素，得到最优设计方案，并通过其内部流动分析探讨最优设计方案性能提高的原因.

1 正交试验优化设计

100QJ10型高速井泵的设计参数分别为流量Qd=10 m3/h，单级扬程H=20 m，转速n=6 000 r/min，级数9级，比转数ns=122，其半剖图如图1所示.数值模拟得到原模型在设计流量下的单级扬程为20.86 m，效率为55.68%.

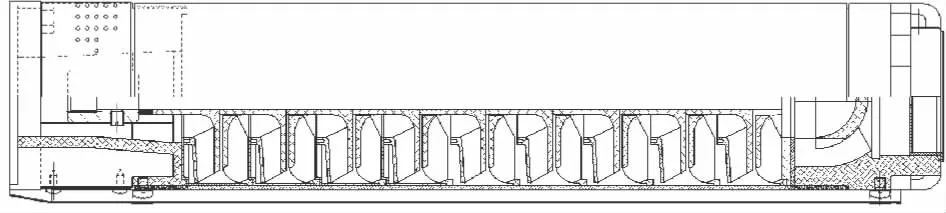
图1 原模型半剖图

1.1 试验目的

1) 分析高速井泵叶轮不同几何参数对效率、扬程的影响规律，找出影响性能的主次因素.

2) 设计要求尽可能提高扬程，通过正交试验分析各因素对扬程的影响，获得扬程最高的方案.

1.2 试验因素和试验方案

所选取的高速井泵模型来自浙江省某企业，该泵采用立式结构，进口端垂直吸入，出口端垂直向上流出，泵轴通过联轴器与电动机直联.模型泵叶轮几何参数分别为叶片出口宽度b2=6.0 mm，叶轮出口直径D2=79.5 mm，叶片数Z=6,叶片出口安放角β2=21°，叶轮进口直径D1=39.0 mm，叶轮后盖板与反导叶最底端轴向距离h=4.0 mm，叶轮出口斜切角度15°，导叶几何参数分别为进口直径84.5 mm,出口直径390.0 mm,叶片数z=6. 在导叶已确定的情况下，叶轮的设计是高速井泵性能好坏的决定性因素.根据专业理论和设计经验，选取叶片出口宽度b2(A)、叶轮出口直径D2(B)、叶片出口安放角β2(C)、叶片数Z(D)、叶轮进口直径D1(E)、叶轮后盖板与反导叶最底端轴向距离h(F)和叶轮出口斜切角度(G)为试验因素，选用三级泵对其进行正交优化.原模型叶轮和导叶三维实体如图2所示.

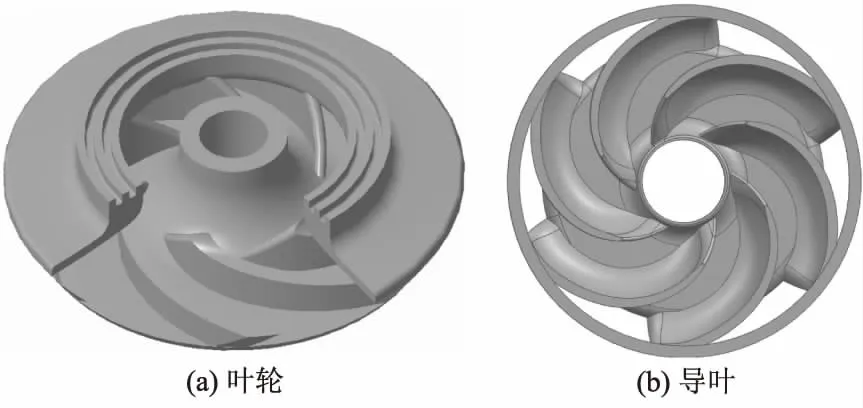
图2 叶轮和导叶实体图

新设计的叶轮要求应与已有的导叶、泵腔匹配，故在不影响高速井泵正常运行的前提下，根据原模型的结构参数以及设计经验，选取合理的水平，以期在该水平范围内使扬程最高，如表1所示.选用 L18(37) 正交表，确定试验方案，如表2所示.

表1 因素水平表

表2 试验方案

2 数值模拟及外特性试验

2.1 数值模拟

2.1.1 三维建模及网格划分

由于高速井泵级数较多，因此数值模拟时需要合理选择级数.文献[9]提出，当多级离心泵的级数增大时，其性能与两级模型基本一致.考虑到计算时间和试验采用了三级泵这一因素，文中选取三级模型进行数值模拟.根据所给的初始模型数据，利用三维造型软件Creo 3.0对各水体部分进行三维建模，然后将其分别导入ICEM中划分网格.整个计算域采用混合网格，导叶部分结构复杂，叶片扭曲严重，容易出现负网格，采用非结构化网格，其余部分采用结构化网格.对交接面网格进行设置，以防止其网格尺寸相差过大.最终单级叶轮网格数约为500 000，总网格数约为5 400 000，叶轮和导叶网格如图3所示.

图3 计算域网格

2.1.2 求解控制及边界条件

划分好网格后，将各部分导入CFX 15.0软件中进行前处理设置.全流场设为三维不可压稳态黏性湍流流场，采用标准k-ε湍流模型，速度和长度分别求解[10-11].整个计算域分为旋转部分的叶轮和其他静止部分.边界条件设速度进口和压力出口.各流体区域采用interface命令进行数据传递，默认湍流强度为5%，固壁边界条件采用无滑移边界条件[12-13].在求解控制中，应用SIMPLEC算法，采用二阶迎风格式离散差分方程，设置最大时间步为1 500，收敛精度为10-5.对扬程进行监测，以此观察数值计算效果，并保证扬程曲线波动在0.1%以内.

2.2 试验验证

2.2.1 外特性试验

为了验证模拟数据的准确性，在浙江台州某企业井泵试验台上对100QJ10型原型泵进行外特性试验，试验台精度为2级.试验时，通过调节阀门控制流量变化，用流量计显示和监控流量大小.压力表测量出口压力，表位差为1.6 m，通过计算可以得到泵的扬程.电压、电流以及功率等数据可在试验终端直接读取.

2.2.2 外特性对比

为了分析模拟结果与试验结果的差异，将2种情况下的单级扬程和效率在不同工况下对比，结果如图4所示.可以看出，在额定流量10 m3/h处，数值模拟的单级扬程为20.86 m，效率为55.68%，而试验的单级扬程为20.39 m，效率为54.16%，相对误差分别为2.25%和2.72%.尽管两者存在一定误差，但变化趋势较为相近，因此可认为此数值模拟具有一定的可信度.

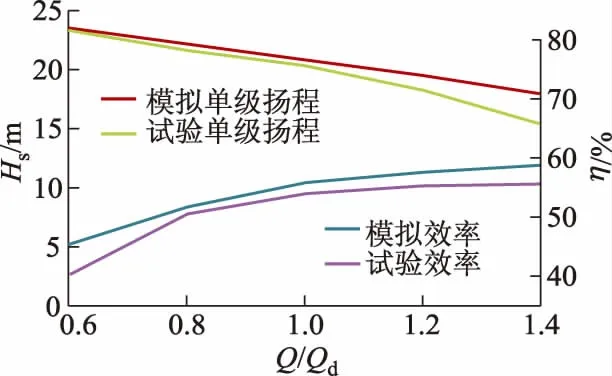
图4 模拟与试验结果对比

3 正交试验结果分析

通过数值模拟，得到18组正交试验方案下的水力性能.选取单级扬程和效率作为评价指标，在额定工况下，对18组方案的数值模拟结果进行分析，如表3所示.极差分析结果如表4，5所示.表中，Ki为每个因素i个水平之和，ki为每个因素i个水平的平均值.通常情况下，ki值越大，该水平下水力性能表现越好.极差R为每个因素中ki的最大值和最小值之差，表示每个因素对性能的影响程度，其值越大说明该因素对试验指标的影响越大，反之则为不重要因素.

表3 正交试验结果

通过对表中的极差值进行对比，可以发现，所选几何参数对高速井泵扬程和效率影响的主次顺序依次为C，G，B，D，A，E，F，对效率影响的主次顺序依次为G，C，D，B，A，E，F.对于单个因素，可以比较其ki值大小确定该因素3个水平对该试验指标的相对最优水平.以因素A为例，由于k3>k2>k1，因此因素A的3个水平对于扬程的影响依次为A3，A2，A1.

表4 额定点扬程分析

表5 额定点效率分析

表6为各因素的3个水平对扬程和效率的影响顺序.

表6 各因素对性能影响的主次顺序

根据设计要求按扬程最高组合选择优化方案，并进行数值模拟，得到额定点的单级扬程为24.61 m，效率为52.47%.对比正交试验的18组方案，最高单级扬程是第8组，其单级扬程为23.37 m，效率为53.7%.相较于第8组方案单级扬程提高了1.24 m.因此确定最终优化方案为A3B3C3D3E3F1G1，该方案下叶轮优化模型各几何参数分别为叶片出口宽度b2=6.5 mm，叶轮出口直径D2=80.5 mm，叶片出口安放角β2=27°，叶片数Z=7，叶片进口直径D1=40.0 mm，叶轮后盖板与反导叶最底端轴向间距h=3.5 mm，叶轮出口斜切角度为0°.

4 优化模型的内流场分析

4.1 外特性分析

为了分析优化方案不同工况下的定常流动，在5个工况(Q= 6，8，10，12，14 m3/h)下对优化模型进行三级高速井泵数值模拟，并进行外特性试验，将模拟数据和试验数据进行对比，如图5所示，可以看出，两者变化趋势依然较为接近.

图5 优化模型试验值与模拟值对比

4.2 内部流动分析

通过对比优化模型和初始模型的水力性能可以发现，优化模型的单级扬程提高了约4 m，换算到九级泵体，其总扬程将提高约36 m，这对该高速井泵性能的提升是十分显著的.为了更进一步研究其性能提高的原因，从内部流动情况来进行深入分析.针对正交试验得到的最终优化模型，选择额定点及其附近的2个工况点，分别对比分析优化模型在额定流量、偏小流量以及偏大流量3种工况下的速度分布与压力分布．

4.2.1 速度分析

图6为优化模型泵在3种工况下首级叶轮中间截面的相对速度矢量分布，可以看出：叶轮内速度分布均匀，无明显回流及旋涡；在靠近叶轮出口处，速度有明显增大，造成这种情况的原因，一定程度上是受到泵腔内壁的影响；随着流量增大，叶轮内流动的高速区逐渐增加，低速区逐渐减少.

图6 叶轮中间截面相对速度矢量分布

4.2.2 静压分析

图7为优化模型泵在3种工况下首级叶轮中间截面的静压分布，可以看出：3种工况下静压都由叶轮进口向出口均匀递增，在此过程中动能逐渐转化为压能；在叶片背面靠近进口处压力相对最小，甚至存在负值，这是由于流体刚进入叶轮，叶片做功能力较弱，静压变化不稳定；在叶片工作面尾部压力达到了最大值.

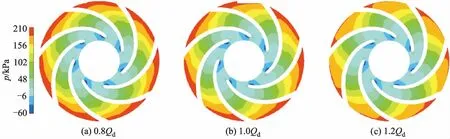
图7 叶轮中间截面静压分布

4.3 优化模型与原模型对比

4.3.1 叶轮中截面静压分布对比

图8为额定流量工况下原模型与优化模型首级叶轮中间截面的静压分布对比，可以看出，优化模型的进出口压差值明显大于原模型，静压梯度变化更为明显，这说明优化模型的扬程要明显高于原模型.

4.3.2 泵体中截面静压分布对比

图9为额定流量工况下原模型与优化模型泵体中间截面的静压分布对比，可以看出：无论是原模型还是优化模型，静压值都随着叶轮的级数增大而增大；对于单个叶轮，首级叶轮的进出口压差要大于次级和末级叶轮，说明首级叶轮的扬程相对较高；优化模型与原模型的进口段静压基本相同，但在出口处，优化模型明显高于原模型，进出口压差也远大于原模型，因此具有更高的扬程.

图8 原模型与优化模型首级叶轮中间截面静压分布对比

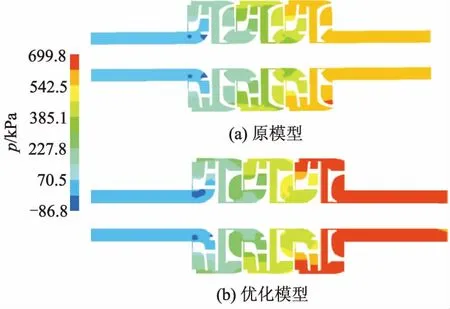
图9 原模型与优化模型泵体中间截面静压分布对比

5 结 论

采用三级泵体进行数值模拟，模拟结果与试验数据吻合良好，可以较好地用来预测高速井泵的水力性能.

1) 采用正交试验设计法研究了叶轮各几何参数对高速井泵性能的影响，结果表明，在适当的因素水平范围内，叶片出口安放角和叶轮出口边的斜切角度对高速井泵的效率、扬程影响较大.

2) 高速井泵优化模型的水力性能与其内部流动关系紧密，计算得到的最优化模型的泵体内无旋涡与回流，能量损失小，静压梯度增大，其扬程能得到极大地提高.