微元法教学现状及教学策略

安磊

摘要：高中物理之所以既难教又难学其中一个重要因素是研究问题相比初中更加具有一般性，一般性的过程其物理量往往是变化的，要解决这个问题就需要掌握科学的物理思想方法，这些思想方法隐藏在知识背后给教与学带来了极大的障碍。微元法是中学物理思想方法中非常重要的一种，其思想就是将整体或整个变化过程无限分割成个体或若干小过程来分析，减小了研究的难度，掌握好微元法，可以提升学生科学思维，为学生提供一个科学的视角去思考问题。本文围绕微元法展开，阐述在教学过程中该如何使用微元法并突破教学困境。

关键词：微元法;高中物理;突破策略

中图分类号：G633.7    文献标识码：A    文章编号：1992-7711（2021）20-0095

从“探究匀变速直线运动位移-时间规律”开始，微元法思想就渗透在整个高中物理教与学的过程中，高中教材中相当多的地方用到了这种思想，但自始至终都没有明确提出这个思想。不仅学生遇到涉及微元法问题无从下手，就是任教老师在很多时候也不能很好地使用这种思想。因此加强微元法在教学中的研究具有普遍而深刻的意义。

一、微元法在高中物理教学中存在的问题

1.对微元法在教学中的作用不重视物理知识

物理解题方法是显性的，教学目标是清晰明确的，而物理思想方法是隐性的、不明确的，因此在课堂中教师很少引导、培养学生微元法的思想的建构。

2.所需数学知识教学进度滞后

微元法从学生学习高中物理开始就会涉及，使用该方法时需要用到数学中“极限”的思想，具体运算过程中往往还会用到数列求和等知识，而此时数学还远远没有讲到这些内容，这种学科之间的关联、辅助作用因教學进度被弱化，缺少数学的表达，导致很多微元法的科学推理过程无法进行。

3.对微元法适用情形、使用方法不清楚

任何一种物理思想方法均有一定适用情形，微元法也不例外，由于教材中自始至终均没有涉及微元法概念的界定和适用情形，导致一些教师与大多数学生对该方法的适用情形是不清楚的，什么情形用微元法、用微元法能解决什么问题。

二、教学策略

1.备课时充分了解学情

掌握微元法需要经历记忆、领会、应用三个基本阶段，教师需要深化理解中学教材中的知识点，熟悉哪些知识点、规律背后蕴藏了微元法的思想，同时要了解使用微元法需要的数学知识学生是否已经掌握，从而制定科学合理的教学目标。

2.归纳总结教材中微元法适用情形及方法

总结归纳高中物理中使用微元法的情形后我们可以得出结论：当所研究的问题中的核心物理量发生连续变化或者我们研究的对象无法用已有的模型、规律去解决时就可以考虑使用微元法，使用微元的思想后一定可以将无法解决的问题变为可以用已知模型、规律去解决。

2.1微元分割方法[1]。使用微元法首先要对研究过程或对象进行无限分割常见的分割方法有以下几类。

（1）线分割。线元，是最常用的微元，通过线分割可以得到质点、点电荷、电流元等。例如分析环形电流产生的磁场时可以将环形导线线分割为无数段小圆弧，取其中一段圆弧，可以将其看成是直线，从而得到直导线电流元，由安培定则可以判断电流元磁场方向，由磁场叠加原理，将每段电流元产生磁场叠加得到环形电流内部磁场方向。

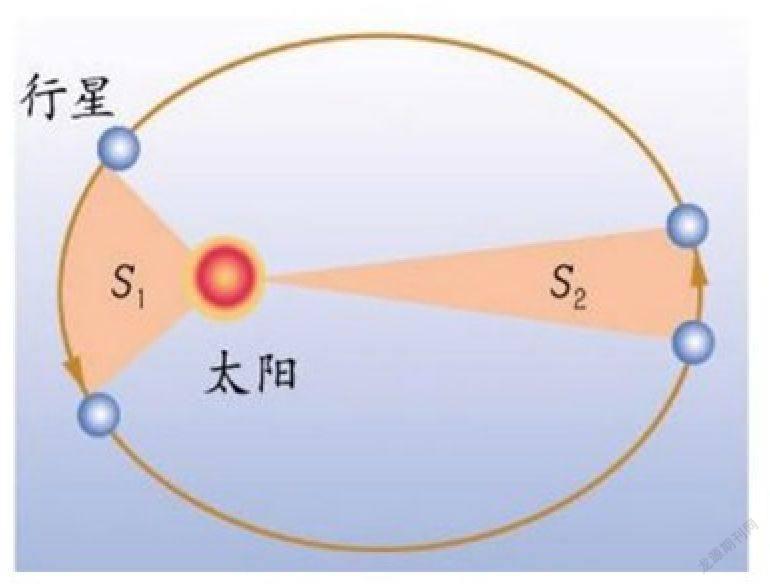
（2）面分割。比如说在人教版必修二第六章第一节“行星的运动中”，学到过开普勒三大定律，其中分析行星在近日点和远日点的速率之比，就用到了面分割微元，如图所示，行星的运动轨迹是椭圆且速率是变化的，但是分割后取的某一小段时间内就可以认为行星是做匀速圆周运动，将整个行星运行轨迹的面分割成几个小扇形，求出扇形面积，利用开普勒第二定律即可求得近日点和远日点的速率之比。

（3）体分割。对体积分割得到的微元叫体积元，从而可以得到质量元、点电荷等。例如在求解质量分布均匀球体对过其直径的轴的转动惯量时，可以将球体无限分割成一个个的质点，求出质点对改轴的转动惯量，再累加就可求出整个球体对转轴的转动惯量。

（4）过程分割。在物理的学习中很多情形是将物理过程分割为许多微过程，选取其中的一段极短时间Δt，在这段极短时间内某些变化的物理量可以看成是不变的量，这样我们就可以用已有的物理规律求出该微过程中重要的物理量，再用累加求和的方法最终解决问题。我们以2013年全国高考课标1卷第25题的第二问为例来说明过程分割的情况

例：如图，两条平行导轨所在平面与水平地面的夹角为θ，间距为L。导轨上端接有一平行板电容器，电容为C。导轨处于匀强磁场中，磁感应强度大小为B，方向垂直于导轨平面。在导轨上放置一质量为m的金属棒，棒可沿导轨下滑，且在下滑过程中保持与导轨垂直并良好接触。已知金属棒与导轨之间的动摩擦因数为μ，重力加速度大小为g。忽略所有电阻。让金属棒从导轨上端由静止开始下滑，求：电容器极板上积累的电荷量与金属棒速度大小的关系;金属棒的速度大小随时间变化的关系。

分析：金属棒下滑过程中速度逐渐增大，我们无法判断其是否在做匀加速直线运动、其加速度满足什么规律、安培力满足什么规律等问题，因此无法用已知的规律直接求解，要求解其速度我们必须先找出加速度、安培力满足的规律，我们将下滑过程分割为无数微过程，在这极短的Δt过程中我们可以认为金属棒受到的安培力为恒力，大小为BLi，金属杆做匀加速直线运动，从而列出牛顿运动定律。金属杆切割的电动势在这段时间内均匀增加，电容器的电荷量均匀增加，由电动势、电容、电流的有关知识即可求解这个问题。

2.2微元法使用的一般步骤及示范。使用微元法首先要根据具体的情景对研究过程或对象进行无限分割，前面已经详细分析了分割的不同情形，分割的微元越精细，微元所遵循的规律就越精确。

在无限分割下研究的变量可视为常量，这里一定要注意我们关注的核心物理量才看作是常量，并不是所有物理量都看作是常量，根据已有知识、规律写出微元所遵循的物理规律。随后检查各微元是否都遵守该规律，这些规律是否具备叠加的特征，是矢量叠加还是标量叠加，这些一定要弄清楚，对核心物理量进行递推、累加从而达到精确逼近。以上操作步骤可归纳为：选择合适的微元分割方式——写出各微元遵循的规律——递推或累加得到整体的规律。

结语：以上讨论给我们很多启发，教师要制定科学合理的教学目标，要对教材中物理思想方法进行归纳总结，要形成清晰明确的使用步骤才能让我们的教学更有针对性，效果更好，更好地落实物理核心素养。

参考文献：

[1]王溢然中学生物理思维丛书分割与积累【M】.安徽，中国科学技术大学出版社2015：79-95

[2]杨振东.微元法教学困境及其突破策略探析[J].湖南中学物理，2020，35（10）：48-51.