基于改进R/S估计算法的网络流量长相关性分析
2021-05-21荣红佳盛虎闫秋婷
荣红佳,盛虎,闫秋婷
(大连交通大学 电气信息工程学院,辽宁 大连 116028)*
水文专家H.E.Hurst经过长期研究发现水文数据存在长相关性(长记忆性),即某一阶段河流流量的数据变化将对以后很长时间的流量数据产生影响.而在此之前的水文数据研究都忽略了水文数据长相关性的存在,从而导致数据模型和流量预测数据不准确[1-2].为了纪念Hurst的发现,使用Hurst指数来描述一个时间序列的长相关性.H.E.Hurst 1951年提出传统R/S估计算法对Hurst指数进行估计,为随机信号的长相关特性分析奠定了基础.Hurst指数估计在股票趋势分析、网络流量预警、交通调度、反恐战备等领域中起着至关重要的作用.而如今大数据时代的来临,带来了海量的数据资源,更是为Hurst指数的研究带来重大的支持.
Hurst指数计算的准确度直接影响着系统模型和预测的准确度,为了提升R/S估计算法的准确性,学者们提出了不同类型的R/S改进算法,对算法性能进行了评价.Mandelbrot B.B.和 Wallis J.R.给出重标极差R/S估计算法鲁棒性分析[3];Lo,Andrew W给出一种改进型R/S估计算法,将长相关分析推广到非高斯信号分析[4];Giraitis L和Kokoszka P等人于2003年给出一种基于V/S统计量的重标度方差估计算法,并分析了算法的可靠性[5].
本文针在对比分析以上研究成果的基础上,对传统R/S估计算法中的重新标度方法进行改进和优化,给出一种基于序列长度公约数的改进R/S估计算法,一定程度上提升了算法准确度和计算速度.此外,将算法应用于真实的网络流量数据长相关特性分析,得到了较好的分析结果.
1 Hurst指数和传统估计算法及相关对比估计算法介绍
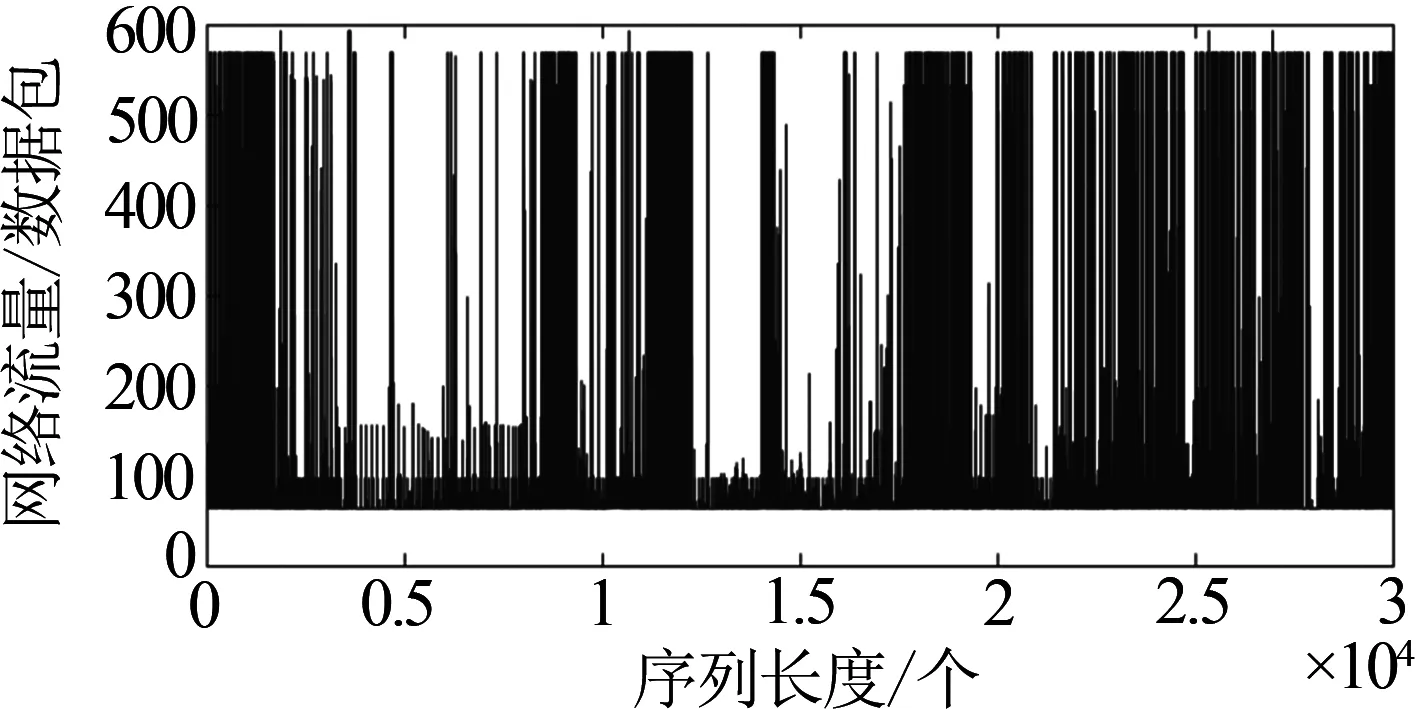
Hurst指数用于测量随机序列的长相关或长记忆特性,当H=0.5时,时间序列就是标准的随机游走,可以认为现在时刻对未来不会产生影响,时间序列是没有记忆性的[6].当0.5 传统R/S估计算法提供了一个标准化的时间序列统计方法,用于揭示随机过程中的长期相关性.传统R/S估计算法是目前为止最常用的Hurst指数估计方法之一,基本思路是研究不同时间尺度条件下时间序列的变化,分为不相关的时间序列和相关的时间序列,研究整体与局部之间自相似性客观存在的统计特性.传统R/S估计算法首先将数据分成长度相等且互不重叠的子序列并计算子序列的均值和离差[8-10],进一步计算极差和标准差得到RS值的标准差,估计得到Hurst指数. 具体的,针对长度为n的时间序列x1,x2,…,xn,传统R/S估计算法的基本步骤如下:首先对序列进行重新标度,重新标度的参考值集合dn={1,2,…,n},即将序列按照集合d中的取值分为n组子序列,每个子序列的长度满足: (1) 然后再对以上每个子序列进行特定的运算,最后得出Hurst指数的值.从式1中可知,传统的重新标度方法中参考值的合集取到了从1~n的所有值,或者间隔某一定数量进行取值,两种方法都未对信息进行刻意筛选,前者导致计算量过大,从而计算效率低,后者几乎必然会导致信息的丢失,从而导致计算出现偏差. 残差方差估计算法针对长度为n的时间序列x1,x2,…,xn,将序列分成大小为m的子块,其中每个子块的部分和为Y(t),最小均方线为a+bt,然后计算其余数的样本方差: (2) 该方差正比于m2H,利用log-log图进行最小二乘拟合,得到拟合直线的斜率为2H,进而可以得到Hurst指数的估计值H. Higuchi估计算法对长度为n的时间序列x1,x2,…,xn,重新构造成一组新的数据: (3) 式中,m,k为整数,分别为初始时间和间隔时间.设定时间间隔为k,则可以构造出k组新的序列.Higuchi法的计算公式如下: (4) 如果给定的序列具有长相关性,那么满足E(Lm(k))∝CmH-2.利用log-log图进行最小二乘拟合,得到拟合直线的斜率为H-2,由此可以得到Hurst指数的估计值H. 所以,传统R/S估计算法中重新标度过程对计算量和准确度影响极大.本文就传统R/S估计算法中重新标度过程提出改进,在提升计算效率和准确度方面具有实际的意义. 对传统R/S估计算法进行改进,首先对时间序列进行重新标度,重新标度的合理性直接影响其计算自相似序列Hurst指数的准确度,算法在重新标度的过程中,第一要考虑信息的完整性,当序列的长度与份数不能整除时,会有一部分信息丢失,从而造成计算出现偏差;第二要考虑计算的效率,例如将序列完全离散化或者直接使用整个序列进行计算,导致包含的信息量过大而没有计算意义. 考虑到以上两点,本文给出了一种基于序列长度公约数的重新标度方法,在1~n的分组策略中,利用公约数可以被整除的特性,挑选出了基于序列长度公约数的集合,既保证了计算时不会出现信息丢失,保证了估算的准确度,由于避免了一些没有意义的计算,也一定程度上提高了计算的效率,节省了计算的时间.针对长度为n的时间序列x1,x2,…,xn,算法的基本步骤如下: (1)找到一个略小于序列长度的参考值n′,其满足n′=μn,μ为一个非常接近1的数,例如μ=0.99,这样可以保证在重新标度时,不会取到整个序列. (2)找到参考值n′公约数的集合d={d1,d2,…,dk}, (5) 其中,i为整数,由于d为公约数的集合.同时d1,d2,…,dk大小依次递增,即公约数从小到大进行排列,为了保证序列在重新标度时,每个子序列的长度不至于太小,所以d1大于dmin,dmin是一个大小合适的数,例如取dmin=50. (3)对序列进行重新标度,将序列分为k组子序列,其每个子序列的长度满足 (6) 其中,dk取自序列长度公约数的集合.得到子序列 (7) (4)计算子序列的均值: j=1,2,…,Ni (8) (5)计算子序列的离差: j=1,2,…,Ni (9) (6)计算累积离差: i=1,2,…,k,j=1,2,…,Ni (10) (7)计算极差: Ri=max(zij)-min(zij), i=1,2,…,k,j=1,2,…,Ni (11) (8)计算标准差: i=1,2,…,k,j=1,2,…,Ni (12) (9)计算RS值: (13) (10)将计算出的各子序列的RS值求平均: (14) 并计算其标准差: (15) 为了分析基于序列长度公约数的改进R/S估计算法的准确性和计算速度,首先采用功率谱快速傅里叶变换方法合成分数阶高斯噪声(FGN:Fractional Gaussian Noise).该合成方法的原理是利用谱合成法构造一定参数的分数阶布朗运动的功率谱密度函数,对功率谱密度函数进行傅里叶逆变换得到分数阶布朗运动随机序列,经过一阶差分便可得到FGN随机序列[11-12].再设定合适的H参数就可以进行FGN的仿真过程.仿真合成Hurst指数分别为0.85、0.8和0.75的长度为30 000的FGN序列,图1给出了H=0.75的FGN序列. 图1 H=0.75的FGN序列 使用改进后的R/S估计算法,对相应H值的FGN序列拟合后的结果如图2所示.其中,星形折线为应用改进后R/S估计算法计算的Hurst值,实线为传统R/S估计算法拟合值,三角折线为Hurst指数为0.75的真实值,点划线为多项式拟合后的Hurst指数估计值,代表了Hurst指数的趋势. 图2给出了改进R/S估计算法和传统R/S估计算法计算H=0.75的FGN序列的对比图,图3将图2中局部区域进行放大,并对直线斜率值进行了标注,对比上图中直线的斜率,可以看出点划线代表的改进R/S估计算法的斜率值更接近三角折线代表的真实值斜率,计算误差也较传统R/S估计算法小,当计算H=0.8和0.85时的FGN序列也可以得出同样的结论. 图2 改进R/S估计算法对H=0.75FGN序列的拟合 图3 改进R/S估计算法对H=0.75FGN序列的拟合局部放大图 表1 本文方法传统Hurst估计算法准确度和计算速度对比 针对长度为30000Hurst指数分别为0.75、0.8和0.85的FGN序列,采用传统R/S估计算法、改进R/S估计算法、残差方差估计算法、Higuchi估计算法进行估计并记录估计值和计算速度.表1给出了四种算法在Intel(R) Core(TM) i5-8250处理器,8G内存,MATLAB2016b版本计算机运行得到的估计值和计算耗时数据,对比数据可以看出在准确度方面: 改进R/S估计算法计相比其余三种估计算法的准确度更高;在计算耗时方面:四种方法耗时从小到大分别为:Higuchi估计算法、残差方差估计算法、改进R/S估计算法、传统R/S估计算法,改进R/S估计算法虽然速度并不是最快,但是相比传统R/S估计算法计算速度提升较大. Hurst指数作为自相似性网络流量的重要指标,对网络流量数据长相关特性的定量研究已成为网络流量特性研究的重点内容,如何快速、有效地估计Hurst指数对于网络流量相关业务的应用具有重要的意义[13-15].为了验证前面所介绍的基于序列长度公约数分段的改进R/S估计算法的有效性,本文采用美国贝尔实验室名为BC-Oct89Ext.TL的网络流量数据结合改进R/S估计算法对自相似性网络流量进行分析和研究.从实际网络流量分别获取五段长度为30000的数据,得到五份原始样本数据并展示其中一份数据样本如图4所示. 图4 网络流量样本数据 利用改进R/S估计算法计算五段网络流量样本数据的Hurst指数,得到的结果如表2所示. 表2 网络流量样本数据Hurst值 从表2可知,应用改进R/S估计算法计算的Hurst指数值介于0.5~1之间,说明网络流量数据具有长期相关性,即该序列具有正的持续性,而且H值虽然在0.5~1之间但更偏向1,H值越大,说明这种正持续性越强.并且随着H值的增大,网络流量数据具有的长相关性变强.应用传统R/S估计算法在计算数据Ⅲ和Ⅴ的Hurst指数值时;应用残差方差估计算法在计算数据Ⅴ的Hurst指数值时;应用传统R/S估计算法在计算数据Ⅲ和Ⅴ的Hurst指数值时;应用Higuchi估计算法在计算数据Ⅱ的Hurst指数值时出现了大于1的情况,无法刻画网络流量数据的长相关特性,计算结果没有意义,因此就准确性和有效性来说,改进R/S估计算法计算结果更精准,因此采用改进R/S估计算法计算得出的Hurst指数值在刻画网络流量数据长相关特性方面显得尤为重要. 本文在计算准确度以及计算速度方面将改进R/S估计算法和传统R/S估计算法、残差方差估计算法、Higuchi估计算法进行对比,从表1中可以看出,改进R/S估计算法对H值不同的FGN序列估计结果相比传统R/S估计算法的计算结果更加准确,计算耗时更少,同时改进R/S估计算法相比残差方差估计算法、Higuchi估计算法,其计算结果也更加准确.对传统R/S估计算法进行重新标度是计算自相似序列Hurst指数的一个有力工具,消除了传统R/S估计法中存在的短期依赖性,扩大了长相关序列适用范围.此外,通过对比H值分别为0.75、0.8、0.85时,传统R/S估计算法和改进R/S估计算法计算自相似序列Hurst指数的计算速度分别提升了9.76倍、10.25倍、10.48倍,极大的提升了计算效率.由此可见,利用公约数分段法对比传统R/S估计算法中随机分段法,由于省去了算法内部一些无意义的计算,所以在计算速度上要上升一个档次,在有限的时间内运用改进R/S估计算法计算自相似序列的Hurst指数极大的缩短了运算时间,提高了后续的计算效率. 表2给出了五段网络流量样本数据经过改进R/S估计算法和传统R/S估计算法计算得出的Hurst指数值,对比了两种方法,发现无论在准确性还是有效性方面,改进R/S估计算法都优于传统R/S估计算法. 传统的R/S估计算法在重新标度方法上存在欠缺,当序列的长度与分段数不能整除时,会有一部分信息丢失,从而造成计算出现偏差,而且传统R/S估计算法在计算长相关序列Hurst指数时效率偏低,无法体现与其他方法在计算序列H值的优势所在.采用公约数分段法对传统R/S估计算法进行重新标度,可以在准确度和效率方面带来明显提升.改进R/S估计算法在网络流量数据分析结果验证了算法的有效性,对网络流量数据长相关性分析提供了一种有效方法.2 基于序列长度公约数的改进R/S估计算法

3 基于序列长度公约数的改进R/S估计算法仿真分析
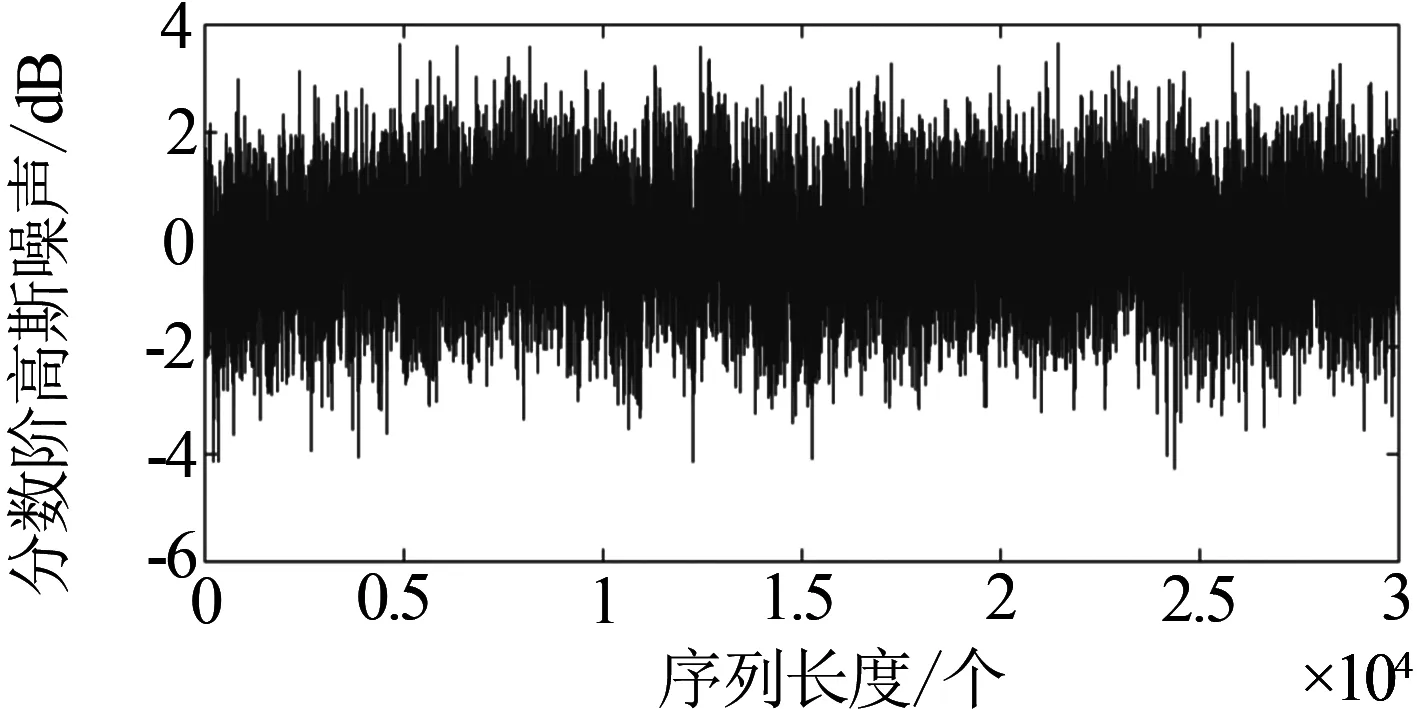
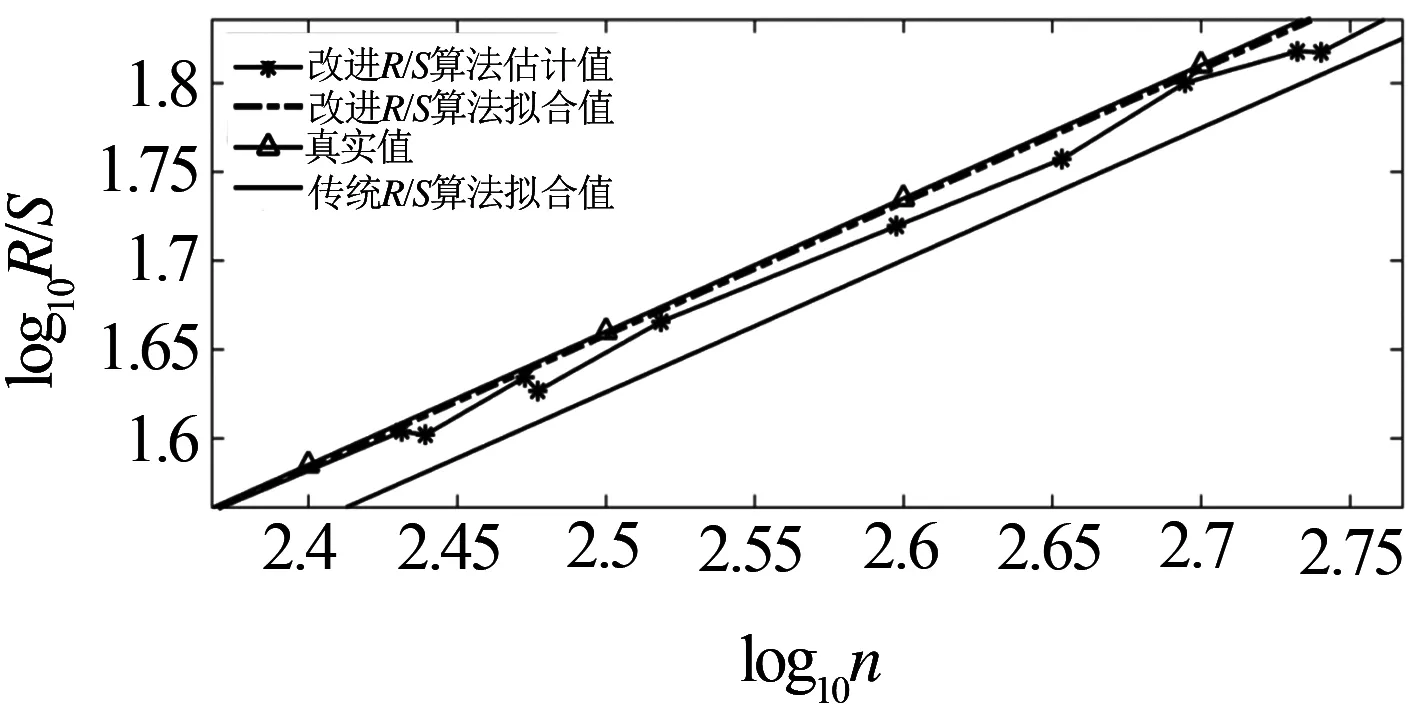
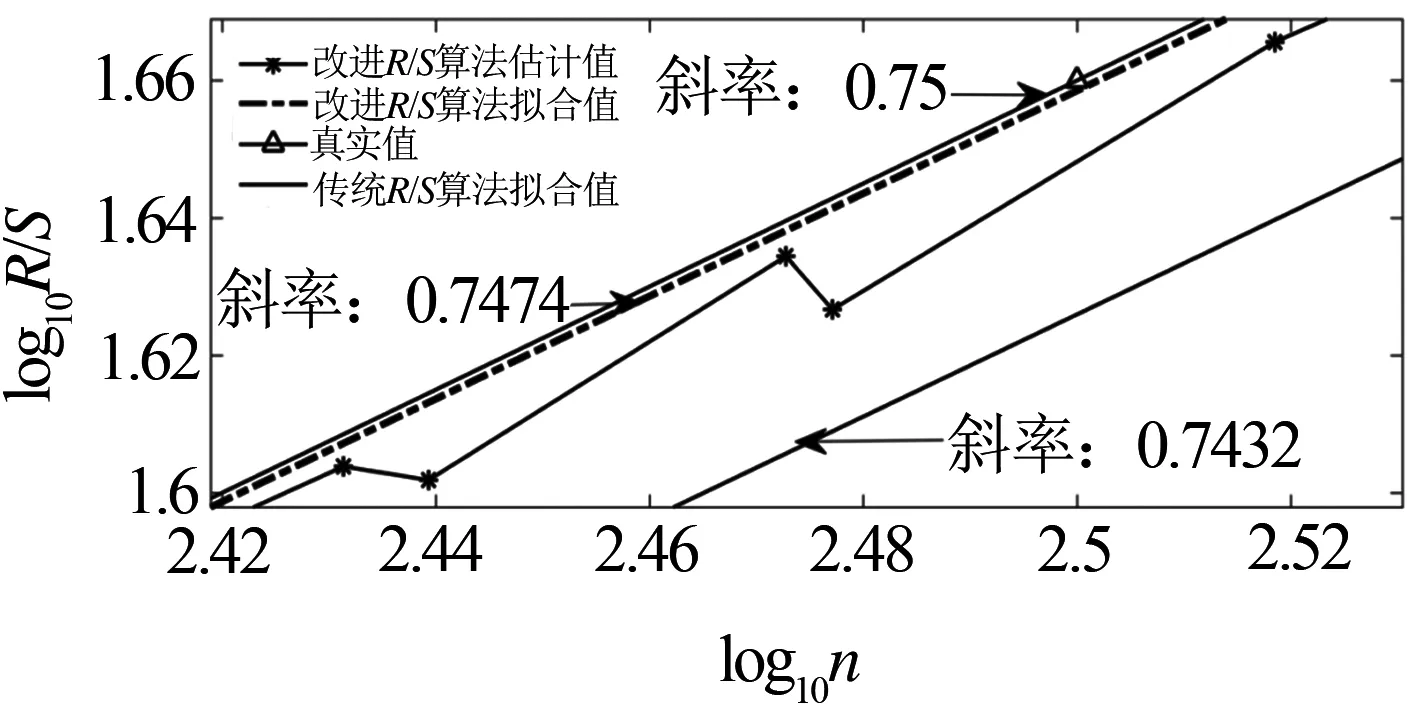
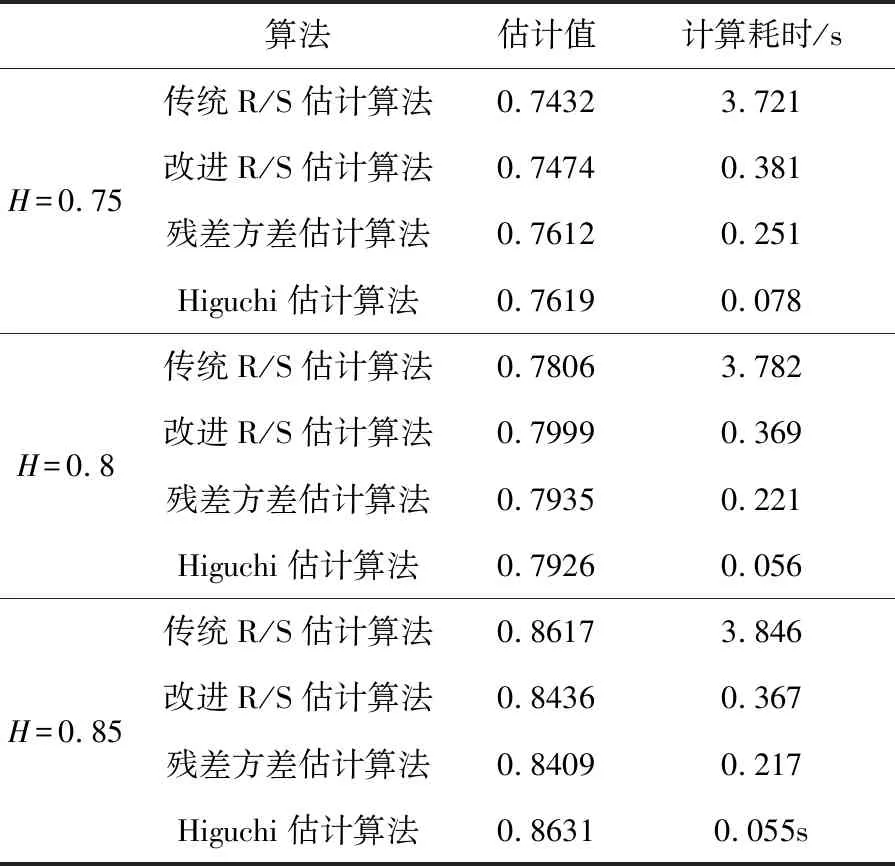
4 改进R/S估计算法在网络流量数据分析中的应用
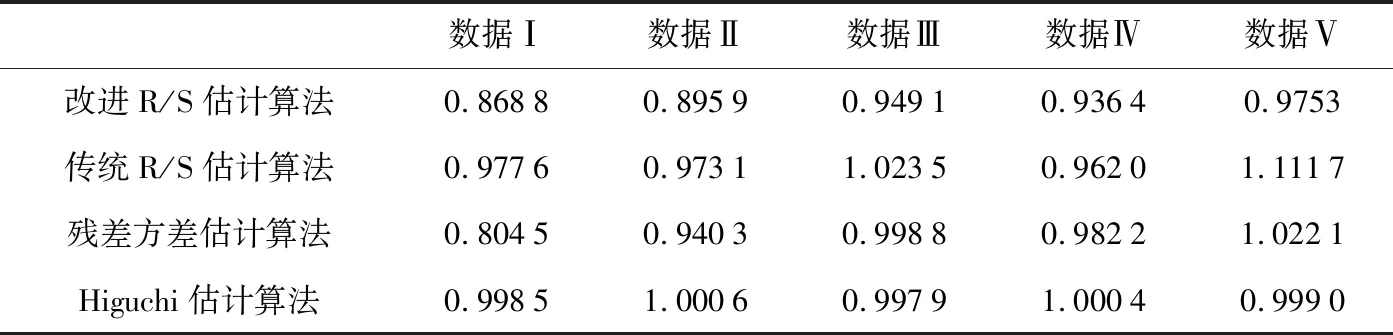
5 结果分析
6 结论
