一种基于键合图模型的未知输入观测器设计

杨大鹏，马付建,刘宇,张生芳，沙智华

(大连交通大学 机械工程学院，辽宁 大连 116028)*

随着控制系统结构和操作的日益复杂化，尤其是系统时变(time-varying LTV)、非线性(non linear)等特性越发明显，经典的线性定常系统(linear time-invariant system LTI)理论已经不能很好地适用于控制系统的特性分析及综合问题[1].系统的复杂化也带来了系统干扰问题，而干扰的存在会诱发系统故障.能否在故障发生时及时地识别故障状态，确定故障位置及故障严重程度对于故障诊断及消除显得尤为重要.由于建模的简化处理,且系统存在一些未知的输入干扰及环境噪声, 各方因素都会直接影响到系统性能,会导致误报.近几十年以来，学者针对故障诊断问题在航空、机电及能源等系统做了大量的研究[2-4].

在解耦干扰方面, 未知输入方法已发展出了很多方法, 如频域方法、未知输入观测器方法、几何方法等[5].其中未知输入观测器(unknown input observer UIO)是系统故障解耦重构的有效方法.其基本思路是通过系统输出的测量来实现系统的重构, 将观测器与系统的输出之差作为残差来判断系统是否存在干扰[6].在进行未知输入观测器设计时，需要对系统结构特性进行分析.其中，系统的不变零点特性对应观测器的存在条件.而通过研究有限结构特性，残差方程的固定极点特性对系统稳定性影响至关重要[7].针对线性时不变系统，未知输入观测器的主要研究方法有几何法[8]、代数法[9]、键合图方法[10-11]等.由于时变特性带来的系统有限结构尤其是不变零点特性的改变，模论方法结合系统键合图模型方法可有效解决线性时变系统未知输入观测问题[11-12].目前，滑模控制[13-14]、线性矩阵不等式[15]、自适应[16]等方法已在非线性系统UIO设计中得到较多的应用.

本文主要针对线性定常与线性时变系统的未知输入观测问题进行研究.在建立系统键合图模型并进行系统特性分析后，采用广义逆矩阵构建系统未知输入观测器.该观测器的设计可以有效运用到系统满足匹配条件的状况.通过对一直线电机模型进行仿真分析，在不同系统及未知输入特性状态下可有效对未知输入进行观测，证明了所提出方法的可行性和有效性.

1 问题描述

考虑一类具有未知输入的线性系统

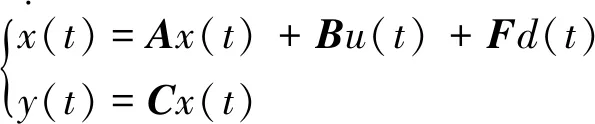
(1)

式中：x(t)∈Rn,y(t)∈Rp,u(t)∈Rm分别为系统的状态、测量输出和控制输入;d(t)∈Rq为系统干扰和建模不确定性等未知输入; 控制输入u(t)和未知输入d(t)有界且无限连续可导.当不存在系统干扰时，线性定常模型用∑(C,A,F)表示，而∑(C(t),A(t),F(t))对应线性时变系统.假设矩阵B，F为列满秩矩阵，矩阵C为行满秩矩阵.

系统强的可探测性(strong detectability)与未知输入观测器的存在与否相关.而强可探测性与最小相条件相关，系统∑(C,A,F)需满足系统零点δ∈(复平面)同时满足如下条件：

(2)

当系统满足强可探测性，并同时满足rank[CF]=rank[F]=q时被称为满足观测器匹配条件(observer matching condition)，该条件为某些未知输入观测器的充要条件.但该条件不能总是得到满足.针对不满足匹配条件的系统，滑模观测器方法可有效解决该问题，并从线性系统扩展到非线性未知输入观测器问题.

2 观测器设计

针对线性系统，文献[17]运用代数学方法提出如下状态观测器：

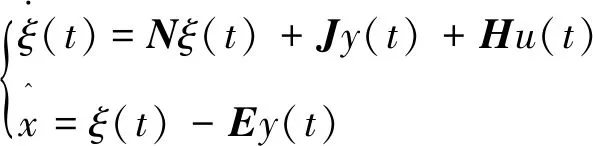
(3)

对于矩阵Am×n，如果其列为线性不相关，那么矩阵ATA可逆.矩阵A的广义逆矩阵可表示为A+=(ATA)-1AT.此时该广义逆矩阵为矩阵A的左逆矩阵：A+A=In.

如果其行为线性不相关，那么矩阵AAT可逆.矩阵A的广义逆矩阵可表示为A+=AT(ATA)-1.此时该广义逆矩阵为矩阵A的右逆矩阵：AA+=Im.

2.1 线性定常系统观测器设计

针对式中的线性定常系统∑(C,A,F)，根据假设条件未知输入矩阵F满足列线性独立.所以矩阵F的广义逆矩阵F+为其左逆矩阵，即F+F=Iq.式中的状态方程可以表达为：

(4)

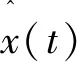
(5)

(6)

式中矩阵N，J，H，E的计算方法及步骤可通过文献[18]查得.通过广义逆矩阵结合代数学方法得到的系统及未知输入观测器系统框图如图1所示.

图1 系统及未知输入观测器系统框图

2.2 线性时变系统观测器设计

线性时变系统∑(C(t),A(t),F(t))通过广义逆矩阵构建状态及未知输入观测器的方法及步骤与上述对线性定常系统∑(C,A,F)类似.区别主要在各矩阵参数具有时变特性，进而影响系统特性，尤其是不变零点.而不变零点与系统的逆系统的极点相关联，从而影响系统稳定性.线性时变系统的状态及未知输入观测器如下式所示：

(7)

令P(t)=I+E(t)C(t)，线性时变系统∑(C(t),A(t),F(t))存在全阶观测器的条件为：

(1)N(t)为Hurwitz矩阵；

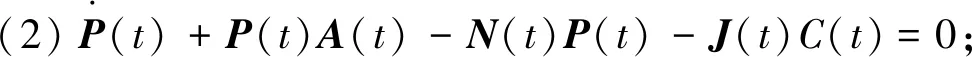
(3)P(t)F(t)=0；

(4)H(t)=P(t)B(t).

(8)

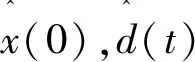
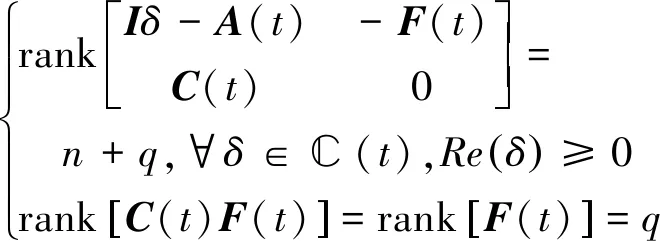
(9)

2.3 键合图方法确定系统强可探测性

如上所述，设计系统状态及未知输入观测器的第一步便是确定系统是否满足强可探测性.这一过程主要分为两步：一是判定匹配条件rank[CF]=rank[F]是否满足，二是系统可探测性是否满足.对于一般系统，此条件的判定过程较为复杂.

键合图是针对多种系统的一种图形化的建模工具，在系统分析过程中有独特的优势.对于单输入输出系统∑(C,A,F)，当其键合图模型中仅存在一条因果路径(causal path)时系统即满足匹配条件.而系统的可探测性与系统的不变零点属性相关. 对于线性定常系统∑(C,A,F)，是否存在零值的不变零点可通过键合图模型进行快速判断.而零值的不变零点的存在不满足强可探测性条件.所以对于系统键合图模型的分析，首先应确定是否存在零值的不变零点.键合图模型可以根据系统分析目的的不同采用不同的因果关系(causality)设置.采用积分因果关系的键合图模型(BGI)可以确定是否存在不变零点.而具有微分因果关系的键合图模型(BGD)可用来确定是否存在零值的不变零点.进一步通过采用双向因果关系的键合图模型(BGB)来确定不变零点的值，当不变零点的实部小于零，强可探测性即得到满足.

3 实验仿真

本节通过一个直流电机系统来验证本文方法的有效性，该系统建模后得到如图2所示的键合图模型，其数学模型如式所示.

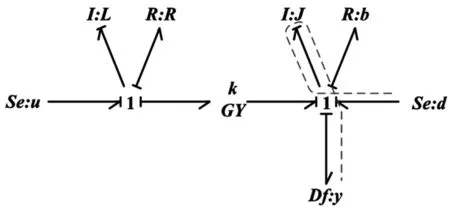
图2 系统键合图模型(积分因果关系)

(10)

通过对系统键合图模型在不同因果关系下的因果路径进行分析，可知该系统可观可控.系统参数如表1所示.

表1 直流电机系统各参数值

通过对系统BGI、BGD及BGB键合图模型分析可知，系统存在一不为零的负值不变零点(δ= -500)，所以系统满足匹配条件及强可探测性条件.由此可见，系统存在如式的未知输入观测器.

3.1 线性定常系统仿真

通过计算可得式中各参数矩阵的具体数值：

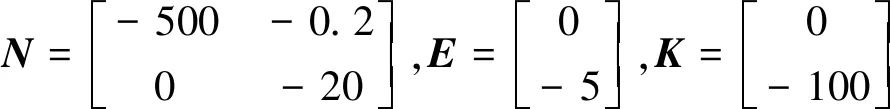
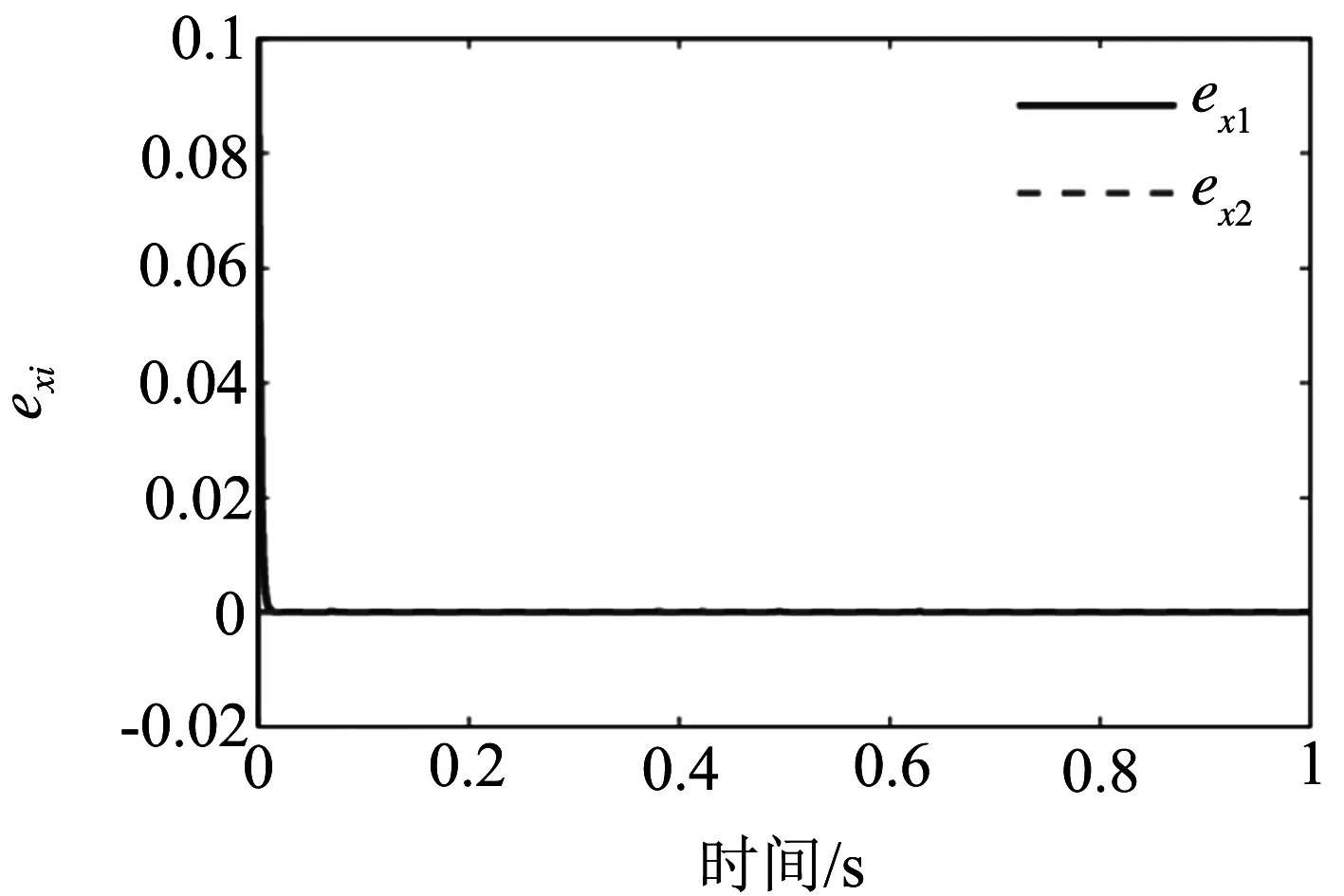
图3 系统∑(C,A,F)状态观测残差分析

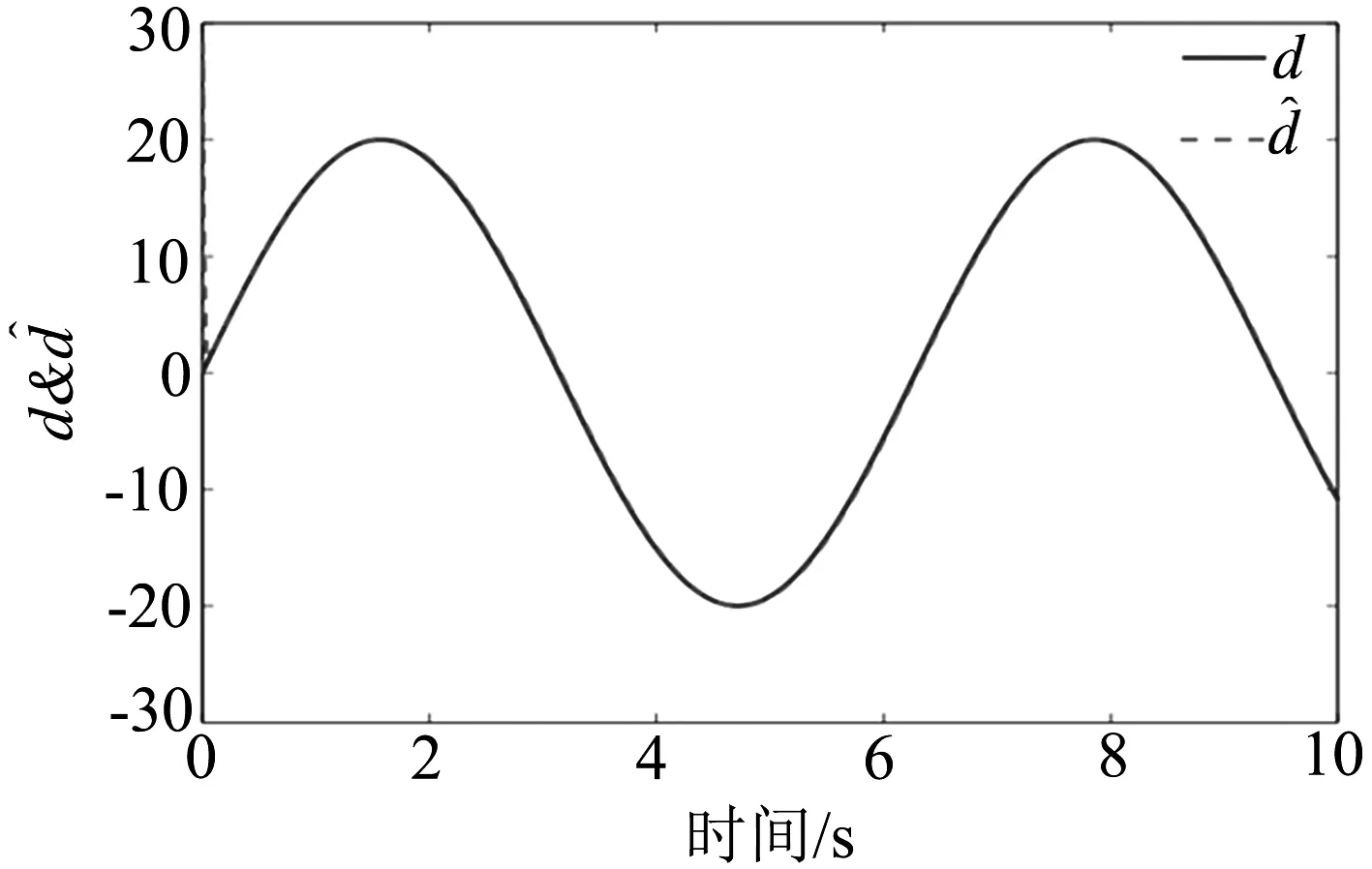
图4 系统实际未知输入变量与未知输入观测量对比

通过图3和图4的仿真结果可以看出，所构建的系统状态及未知输入观测器可以快速准确的对系统∑(C,A,F)的状态及干扰输入变量进行观测.

3.2 线性时变系统仿真

针对线性时变系统仿真，令表1中的参数k=cos(t)+1.2,系统∑(C,A(t),F)变为时变系统，即矩阵A(t)具有时变参数.因为时变特性引起的系统零极点属性的改变，时变系统的难点在于极点配置.通过矩阵计算，时变系统∑(C,A(t),F)的不变零点仍满足δ= -500.系统∑(C,A(t),F)具有式形式未知输入观测器，通过矩阵计算各参数矩阵为：

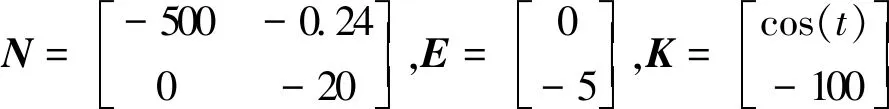
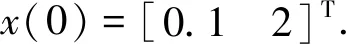
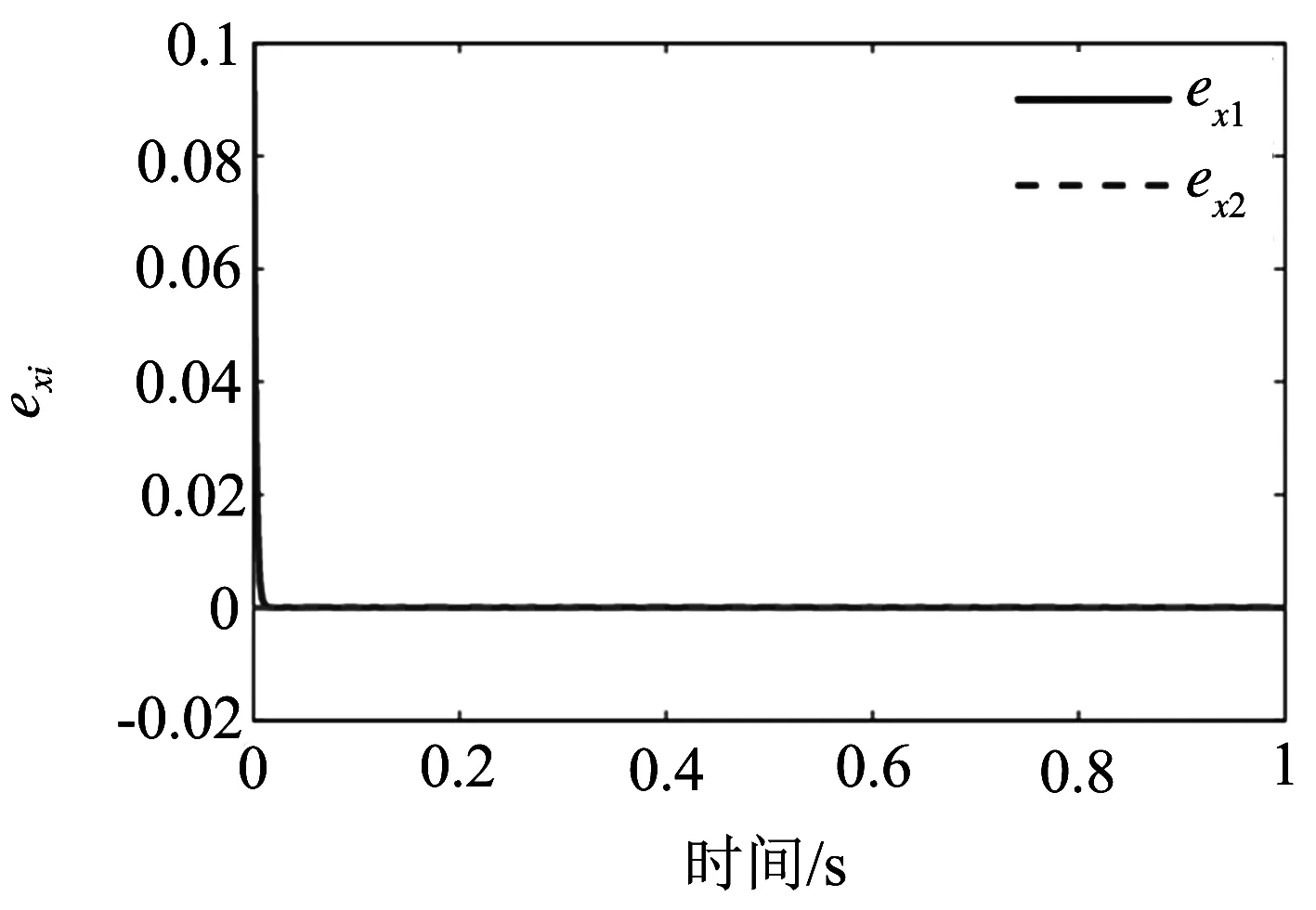
图5 系统∑(C,A,F)状态观测残差分析

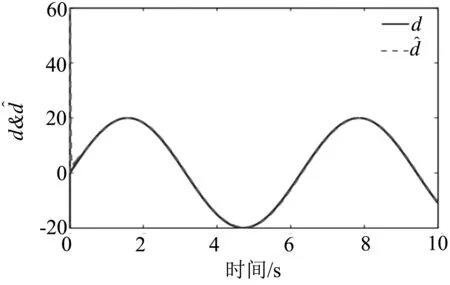
图6 时变系统未知输入实际与观测量对比

通过图5和图6的仿真结果可以看出，对时变系统∑(C,A(t),F)所构建的系统状态及未知输入变量观测器也可以快速准确的对的状态及干扰输入变量进行观测.

4 结论

本文提出了一种针对满足匹配条件的线性定常和线性时变系统状态变量及未知输入变量观测器设计方法.该方法利用广义逆矩阵结合代数学方法构建未知输入观测器.针对系统是否满足匹配条件，利用线性系统键合图模型给出了图形化判定方法.同时给出了利用键合图模型对线性定常和时变系统不变零点及观测器极点配置的方法.本文所提未知输入观测器方法不需要复杂的计算,适用范围更广. 最后,将本文设计的未知输入观测器应用到直流电机系统的未知输入重构中,仿真结果表明了本文所提方法的可行性和有效性.