基于试验设计的空调管路结构参数优化设计

王枫，周文广,2

(1.大连交通大学 机车车辆工程学院，辽宁 大连 116028;2.柳州铁道职业技术学院 动力技术学院，广西 柳州 545616)*

振动是评价空调品质的一项重要指标.空调振动的主要激励源是压缩机，管路是空调振动的主要传播途径[1].空调管路由于压缩机的振动传递容易产生振动，严重时会加速管路的疲劳断裂导致冷媒泄漏，缩短空调使用寿命.因此优化空调管路结构，尽量消除管路振动，提升空调产品性能，具有重要的现实意义[2].

近年来国内外学者在空调管路的振动特性和结构优化方面做了大量研究.S.K.LOH和卢建伟[3-4]采用样机试验的方法验证了空调管路的模态分析结果和谐响应分析结果，表明运用有限元分析技术可以对空调管路进行优化设计.Naohiro[5]通过研究管路的振动情况，得出管路直径和长度是影响管路振动的主要参数.单国伟和B.A. Khudayarov[6-7]采用改变管路长度的方法实现了改善管路模态特性的目的.张晓伟和O.O.R Famiyesin[8-9]研究了管路壁厚对管路模态和振动响应的影响，通过增加壁厚改变管路的固有频率值，改善了管路的模态特性和降低了管路振动的最大位移值.刘浩友[10]通过调整管路的弯曲半径，降低了管路振动的最大位移值和最大应力值.赵文龙[11]通过优化管路的空间角，使管路固有频率远离压缩机激振频率，避免了管路共振.目前的研究都是通过单参数优化来改善管路模态特性和降低管路振动响应，实现提升管路抗振性能的目的.实际上管路的不同结构参数对管路振动性能均有影响，单参数优化未必获得系统的全局优化.比如增加壁厚和管路长度虽然可以改善管路的振动特性，但也增加了系统的质量.如果片面追求管路的设计余量而忽略经济性，则会提高生产成本.因此有必要对空调管路进行多参数多目标优化，通过优化管路结构参数降低管路振动响应，提升管路抗振性能的同时减小管路的质量从而降低生产成本，获得最佳的管路设计方案.

为此本文提出了一种基于试验设计和遗传算法的空调管路结构多目标优化设计方法，不仅提升了管路抗振性能，还实现管路的轻量化.首先利用正交试验设计及方差分析法来确定不同结构参数(包括管路长度、管路折弯半径，壁厚以及管路空间角度)对管路振动最大位移和振动最大应力的影响显著性大小，挑选出显著结构参数，并通过二阶响应面近似模型拟合显著结构参数与管路振动最大位移、振动最大应力及管路质量的映射关系，最后采用非劣排序遗传算法(NSGA-II)对二阶响应面近似模型进行目标值寻优，获得最终的管路优化方案.

1 空调管路振动理论基础

空调管路结构是一个多自由度振动系统，其振动微分方程可表示如下[12]：

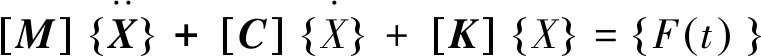
(1)

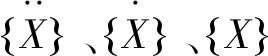
为了得到空调管路的模态特性，即固有频率和振型，需要进行模态分析.模态分析时一般忽略阻尼且激振力为零，因此振动微分方程(1)可简化为：

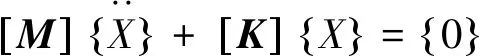
(2)

因为自由振动能够分解成一组简谐振动的叠加，可设上式有简谐形式解：

X={X0}cosωt

(3)

式中：{X0}代表振型，ω代表振型对应的固有频率，将式(3)代入式(2)化简可得：

([K]-ω2[M]){X0}={0}

(4)

由于{X0}为非零向量，则矩阵([K]-ω2[M])对应的行列式为0，即：

det([K]-ω2[M])={0}

(5)

求解微分方程(5)的特征值ωi及对应的特征矢量{Xi}，即可得到系统固有频率及振型.

为了得到空调管路承受压缩机对其施加的周期性激振力时的振动响应大小，需要对管路进行谐响应分析.谐响应分析时，式(1)中的激振力{F(t)}和位移量{X}都设为简谐函数，频率相同为ω，以复数形式可表示为：

{F(t)}={Fmaxeiψ}eiωt=({F1}+i{F2})eiωt

(6)

{X}={Xmaxeiψ}eiωt=({X1}+i{X2})eiωt

(7)

将式(6)和(7)代入式(1)可得：

(-ω2[M]+iω[C]+[K])({X1}+i{X2})=

({F1}+i{F2})

(8)

求解式(8)即可得到管路的振动响应值.而这些求解过程通过合理设置有限元分析软件得以实现.

由式(8)可知，空调管路的振动特性由质量矩阵、阻尼矩阵、刚度矩阵和激振力共同控制，因此在不改变激振力大小和激振频率的情况下，可以通过改变管路长度、折弯半径、壁厚以及空间布局等结构设计参数的方式来提高管路的抗振性能，避免发生共振和引起过大的振动响应.

2 空调管路的有限元分析

2.1 空调管路有限元模型的建立

将某空调管路的三维模型导入ANSYS Workbench进行模型简化和网格划分，所建有限元模型如图1所示.考虑到冷凝器和蒸发器体积大且振动位移小，故将与冷凝器和蒸发器连接的两段管路的末端施加固定约束.压缩机底座的橡胶垫面和气液分离器的底部也施加固定约束.有限元模型中管路的材料为紫铜，四通阀的材料为黄铜，压缩机材料为钢，压缩机底座材料为橡胶.

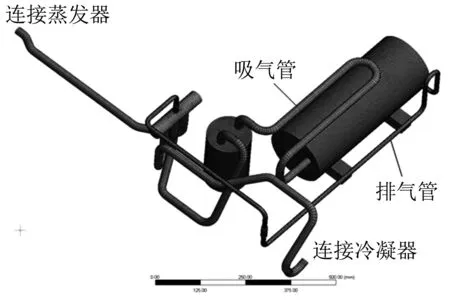
图1 空调管路有限元模型

2.2 空调管路模态分析

利用ANSYS Workbench软件对空调管路进行模态分析.本文研究的空调管路系统中，涡旋压缩机的工作频率为60 Hz，根据管路模态分析所提取的频率至少为工作频率2倍的原则，本文提取了管路的前16阶模态列入表1[13].由表1可知，管路的第6阶固有频率值为61.458 Hz，和压缩机的工作频率60Hz很接近，极易引起管路共振.提取空调管路的第6阶模态振型图，如图2所示. 管路振动的最大位移值发生在吸气管U形弯处，吸气管在水平方向上前后摆动.

表1 空调管路系统前16阶固有频率 Hz

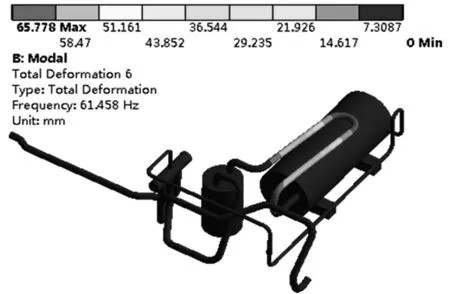
图2 空调管路第6阶模态振型图

2.3 空调管路谐响应分析

空调管路振动的主要激振力是涡旋压缩机因转子不平衡旋转而产生的激振力[14].基于60 Hz下涡旋压缩机激振力的工况，在压缩机有限元模型的转子中心施加一个9 967.2 N·mm的切向力矩和大小为561 N的径向力来代替压缩机转子不平衡旋转而产生的激振力.本文应用模态叠加法对空调管路进行谐响应分析.后处理得到的位移云图和应力云图分别如图3、4所示.

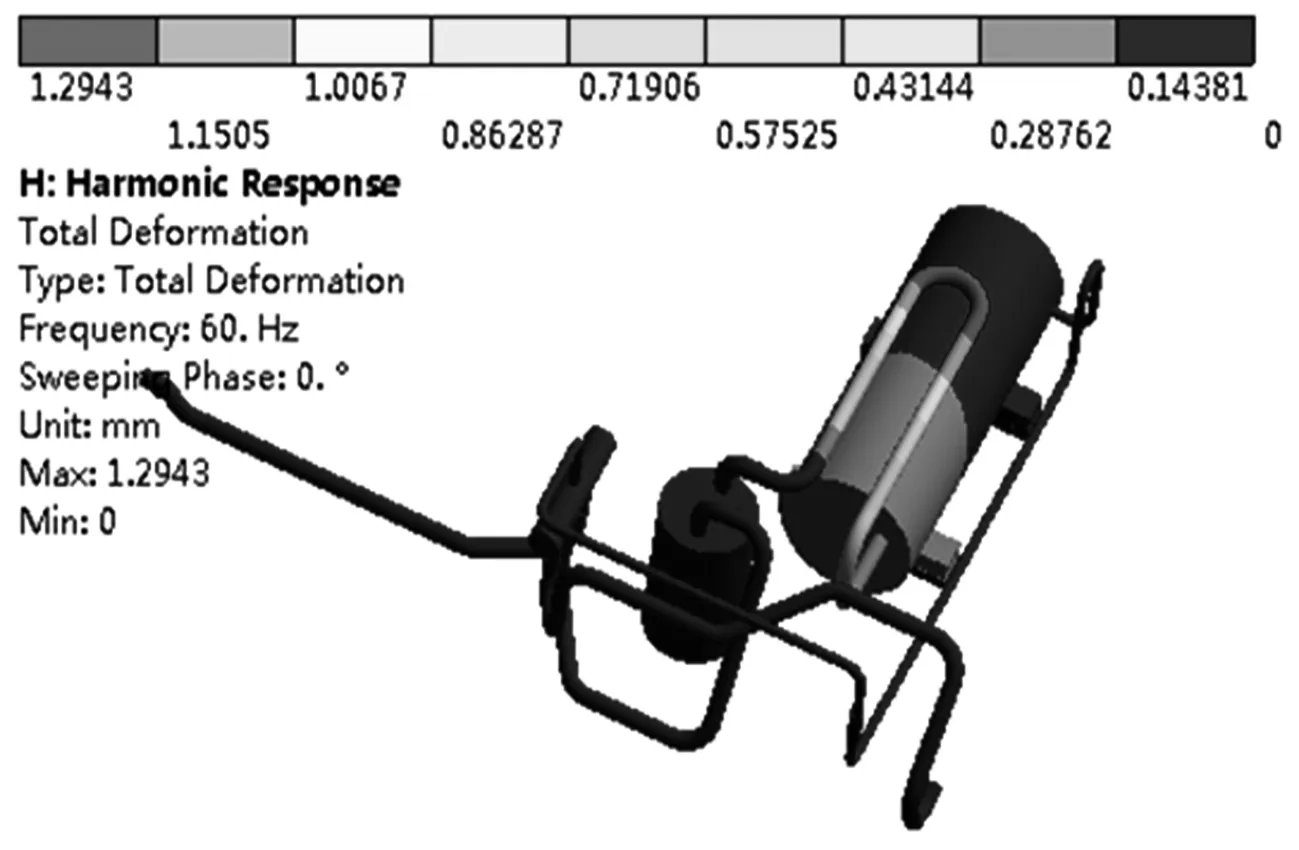
(a) 管路系统位移图

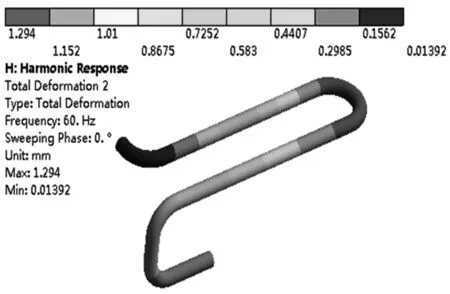
(b)吸气管位移图图3 空调管路谐响应分析位移云图

(a)管路系统应力图

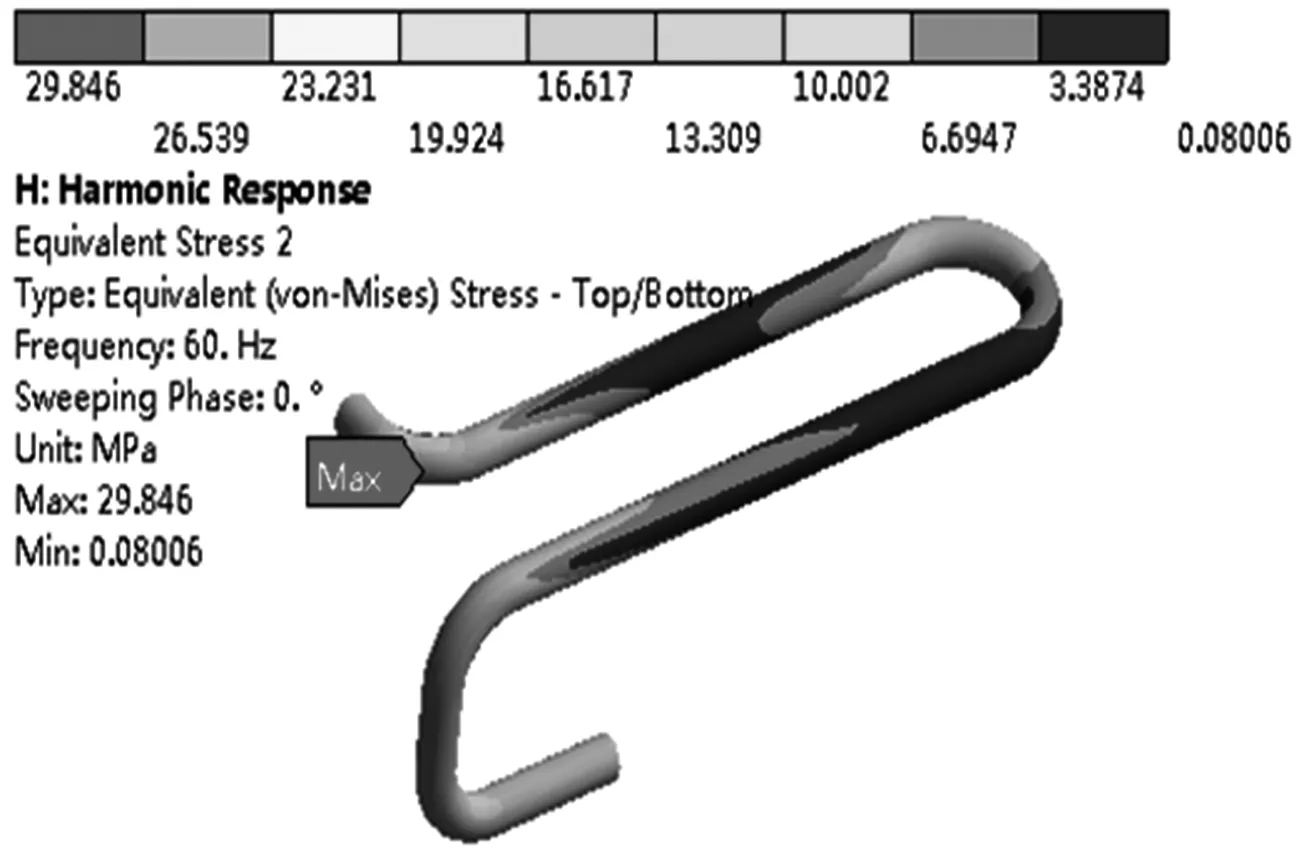
(b)吸气管应力图图4 空调管路谐响应分析应力云图

由图3可知，管路系统中振动位移最大的部件是吸气管，最大位移为1.294 3 mm，位于U形弯的端部.由图4可知，管路系统中最大应力为29.829 MPa，发生在吸气管离气液分离器最近的折弯位置.一般情况下，管路位移应小于1 mm，应力小于20 MPa[10].从谐响应分析结果可知，吸气管的最大位移和最大应力值都超过允许值，吸气管容易产生疲劳损坏.

由空调管路的模态分析结果和谐响应分析结果可知，吸气管是空调管路中极易产生共振和引起过大振动响应的部件，因此有必要对吸气管进行结构优化设计来改善管路的模态特性和降低管路振动响应，使空调管路固有频率远离压缩机工作频率，避免发生共振现象，实现提高管路抗振性能的目的.

3 空调管路结构优化设计

3.1 正交试验及参数影响显著性分析

为了确定管路不同结构参数及其交互作用对管路振动性能的影响显著大小，采用正交试验和方差分析相结合的方法对其进行研究[15].基于空调管路的模态分析结果和谐响应分析结果，确定吸气管为优化对象，在不改变吸气管两端位置的情况下，选取吸气管的管路壁厚x1、折弯处与压缩机端部之间的管路长度x2、管路折弯半径x3、管路空间角x4和U形管的长度x5这5个结构参数(如图5所示)作为试验因素.吸气管的振动最大位移值和最大应力值为试验指标.

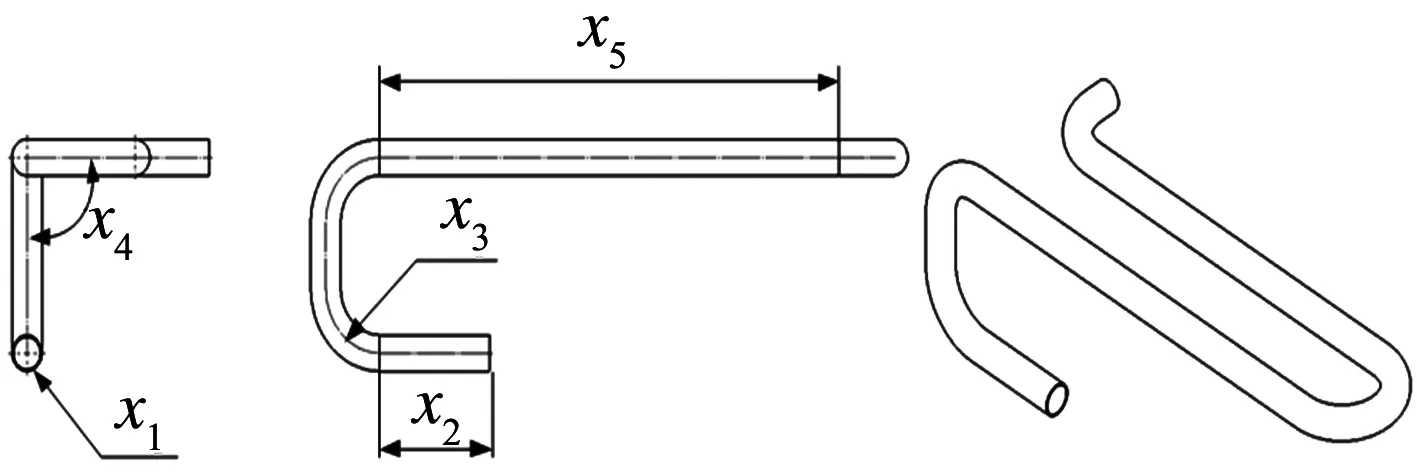
图5 正交试验因素示意图

选用5因素2水平有交互作用的正交表L32(231)安排试验，各试验因素及其对应水平如表2所示.

表2 正交试验因素水平表

根据表2的各结构参数水平重新进行有限元仿真计算，得到吸气管在在各个因素水平下管路振动最大位移值和振动最大应力值.并运用方差分析中的F检验法来判定各试验因素及其交互作用对管路振动最大位移和最大应力的影响显著程度[16].选取显著性水平α=0.25，当变量的F值大于临界值F0.25(1,16)=1.42时，认为该因素作用显著，否则不显著.空调管路振动最大位移和振动最大应力的正交试验显著性分析表分别如表3和表4所示.

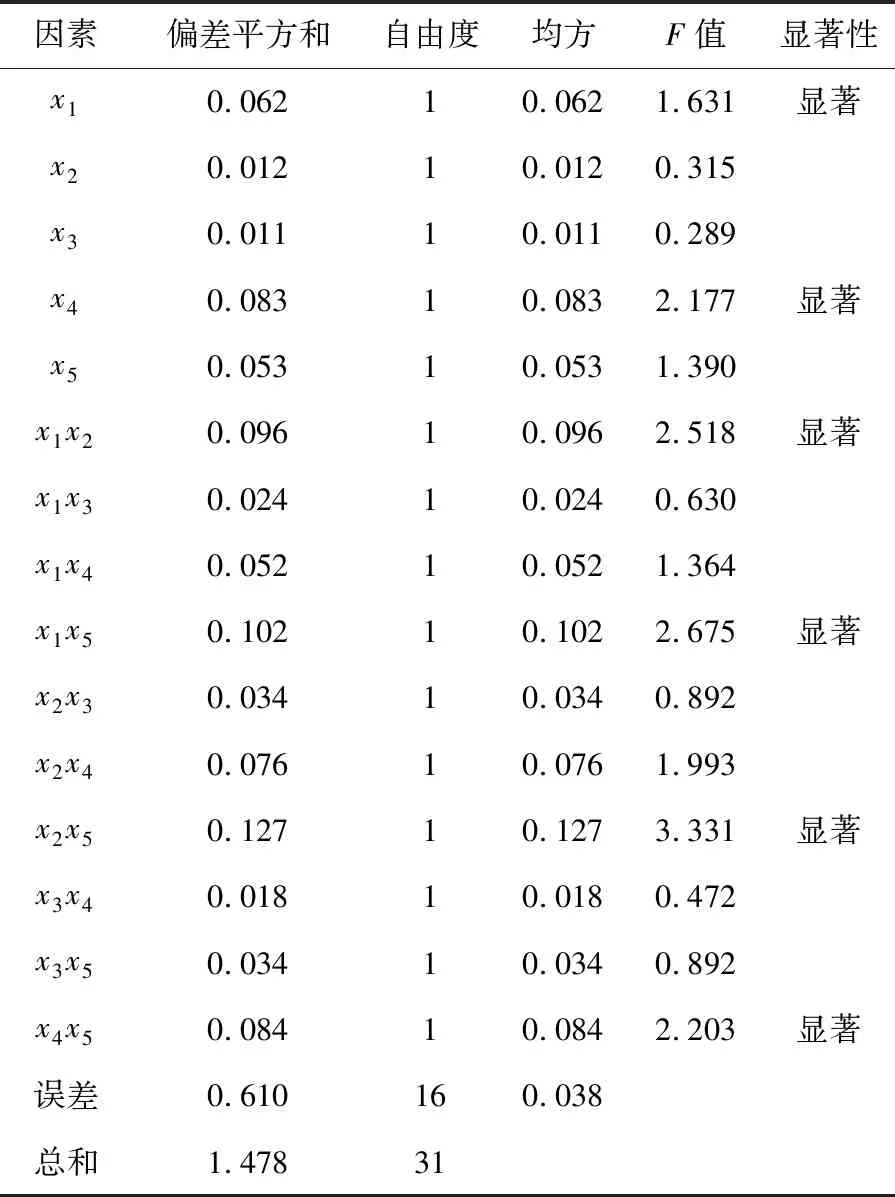
表3 管路振动最大位移正交试验显著性分析表

(1) 管路结构参数对管路振动最大位移影响

由表3中可知，在所研究的管路结构参数中，不同因素对管路振动最大位移的影响显著性大小顺序为折弯处与压缩机端部之间的管路长度和U形管长度的交互作用>壁厚和U形管长度的交互作用>壁厚和折弯处与压缩机端部之间的管路长度的交互作用>空间角和U行管长度的交互作用>空间角>壁厚.

(2) 管路结构参数对管路振动最大应力影响

由表4可知，在所研究的管路结构参数中，不同因素对管路振动最大应力的影响显著性大小顺序为空间角>折弯处与压缩机端部之间的管路长度和U形管长度的交互作用>壁厚和U形管长度的交互作用> U形管长>空间角和U形管长度的交互作用>壁厚和折弯处与压缩机端部之间的管路长度的交互作用>壁厚和空间角的交互作用>折弯处与压缩机端部之间的管路长度和空间角的交互作用>壁厚.

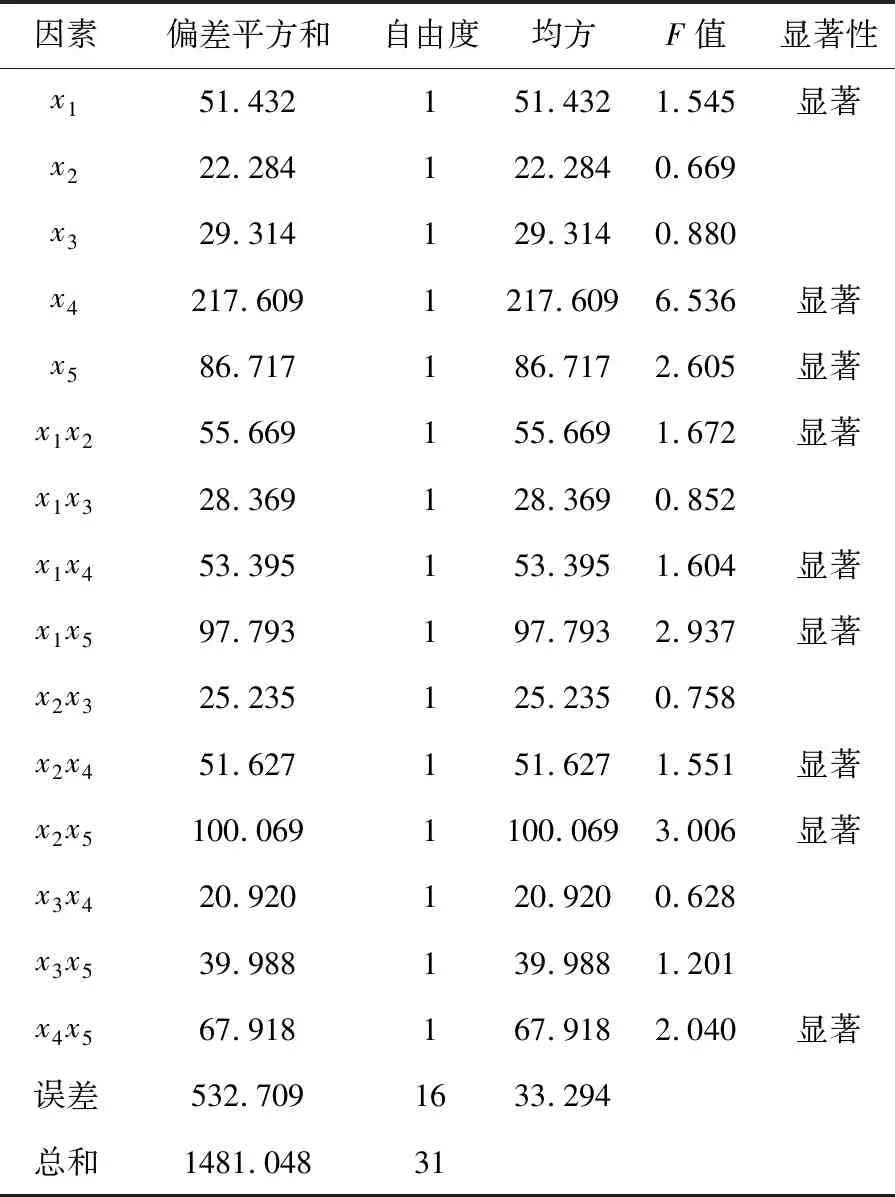
表4 管路振动最大应力正交试验显著性分析表

综上可知，管路结构参数中的管路壁厚x1、折弯处与压缩机端部之间的管路长度x2、管路空间角x4和U形管的长度x5以及它们之间的交互作用对管路振动性能的影响较为显著.只要对这四个影响显著的结构参数进行优化，即可达到改善管路的振动性能和提升管路抗振性能的目的.

3.2 管路响应面模型构建

在空调管路的有限元分析中，管路振动最大位移和振动最大应力是管路结构参数的隐式函数，没有明确的表达式.响应面模型是采用多元回归方程来建立因子与响应之间的函数关系.因此采用二阶响应面近似模型来拟合管路结构参数与响应目标之间的函数关系，其形式为：

(9)

式中：b0为近似模型常数项；bi为近似模型一次项系数；bij为近似模型平方项和交叉项系数；m为设计变量数，取值为4.

为了保证构建二阶响应近似模型的样本点在整个函数的取值空间内分散均匀，且样本数据有代表性，运用均匀试验设计方法对管路结构参数进行试验设计[17]，由于篇幅所限，取部分均匀试验设计结果如表5所示.

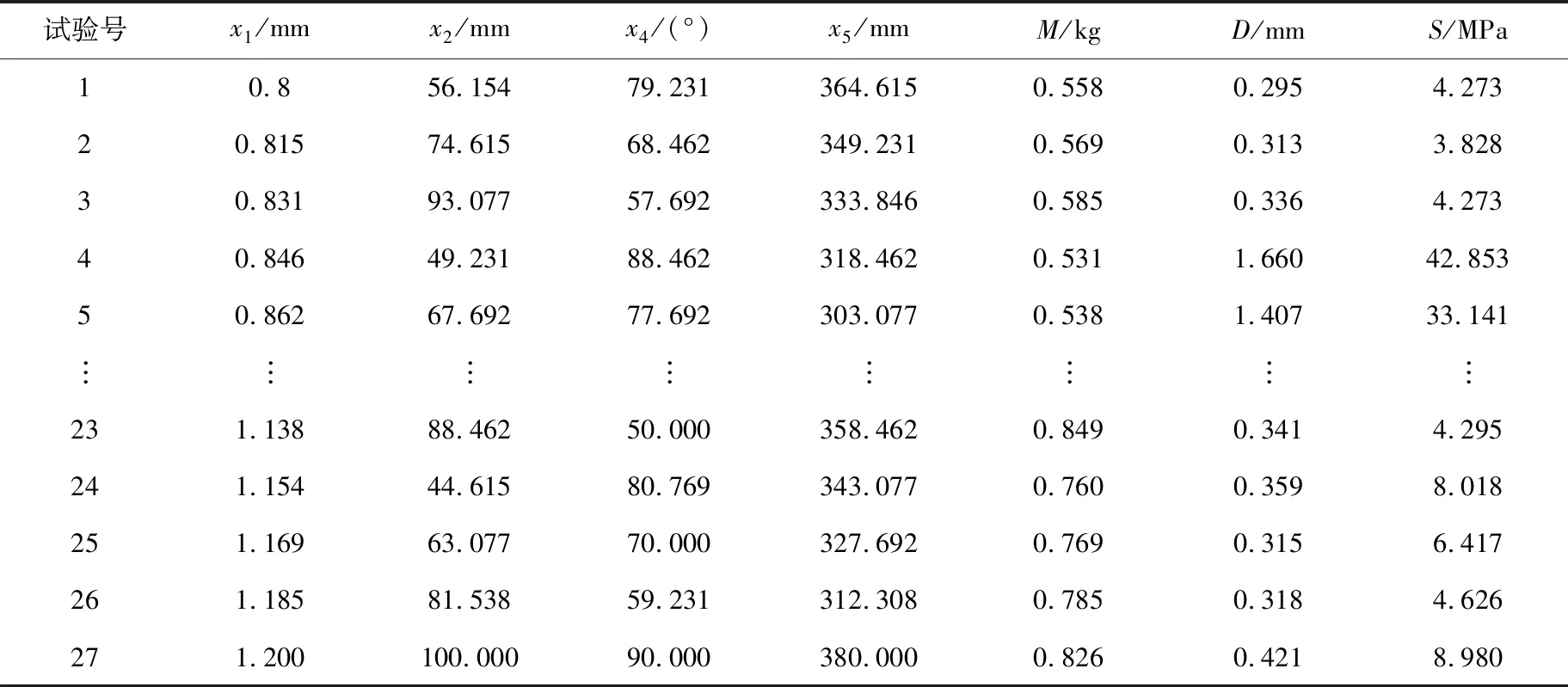
表5 均匀试验设计数据(部分)

根据表5可拟合出管路质量的二阶响应面表达式为：

(10)

管路振动位移值的二阶响应面表达式为：

(11)

管路振动应力值的二阶响应面表达式为：

(12)

3.3 空调管路优化设计

以上文得到的管路结构参数与响应目标之间的映射关系为优化模型，管路质量最轻，管路振动最大位移最小，管路振动最大应力最小为优化目标，则空调管路的优化数学模型可表示为：

(13)

多目标优化求解不存在唯一的全局最优解，而是不同目标在不同权重系数下组合的一系列解的集合，这个集合也被称为Pareto最优解集[18].非劣质遗传算法(NSGA-II)是基于Pareto最优概念演化来的一种改进的非支配排序遗传算法，且求解精度高、收敛快.故本文采用NSGA-II求取Pareto前沿.算法中初始种群数设置为100，交叉分配指数为20，变异分配指数100，经400次迭代计算后，得到Pareto前沿，如图6所示.

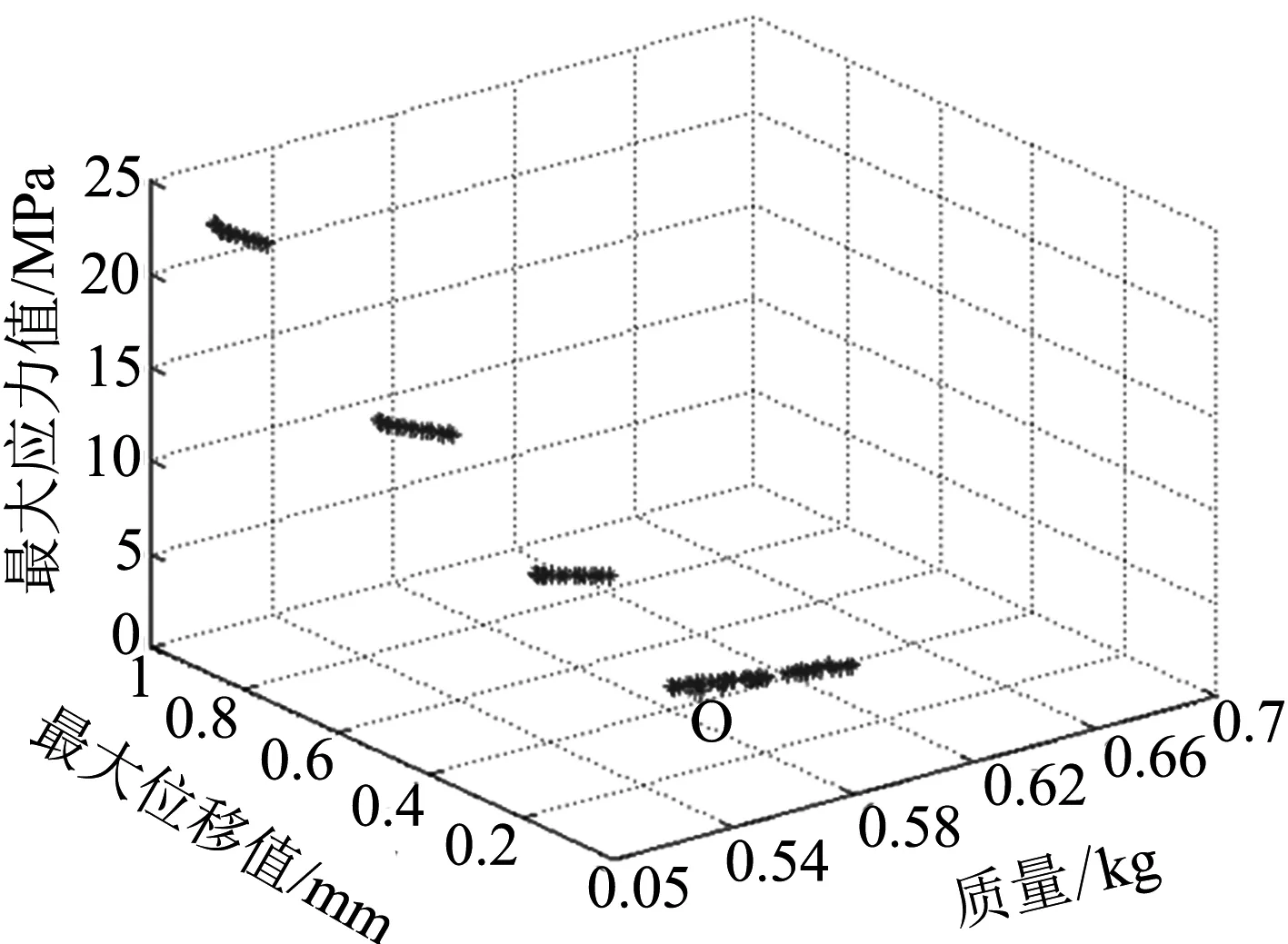
图6 NAGS-II算法Pareto最优解集

在Pareto最优解集中，考虑到将管路质量、管路振动最大位移和管路振动最大应力同时处于一个相对最优的条件下，选取管路振动最大位移和最大应力均较优的O点作为满意解(如图6所示).将O点所对应的管路进行谐响应分析，其结果如表6所示.由表6可知，优化后管路质量从0.779 kg减小到0.567 kg；管路系统最大位移由1.294 mm下降到0.304 mm，小于管路设计的位移允许值1 mm；管路系统最大应力由29.829 MPa下降到3.957 MPa，小于管路设计的应力允许值20 MPa.优化后的空调管路系统模态分析结果如表7所示.从表7可以看出，优化后的空调管路系统的前16阶模态的固有频率均避开了压缩机的工作频率60 Hz，大大降低了管路共振的可能，管路的抗振性能得到很大的提高.

表6 优化前后设计变量和目标响应对比

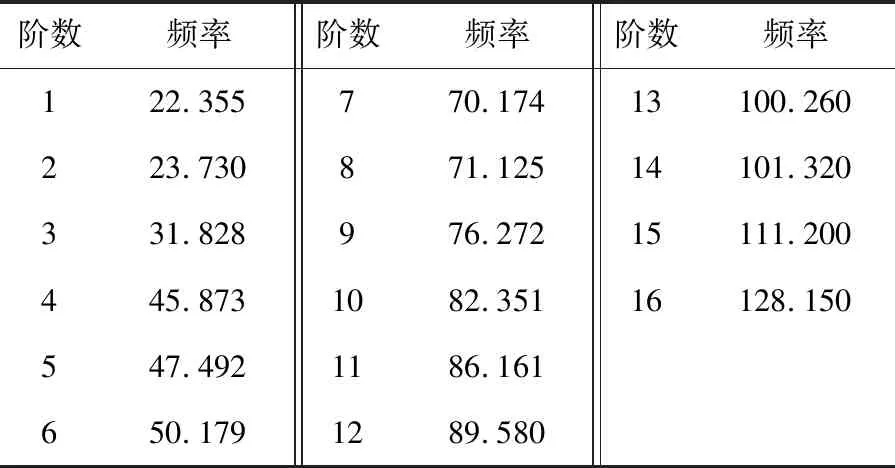
表7 优化后的空调管路前16阶固有频率 Hz

4 结论

(1)由空调管路系统的模态分析和谐响应分析可知，吸气管的第6阶固有频率与压缩机激振力的频率值相接近，因此引起剧烈振动;

(2)通过正交试验和方差分析，获得了管路结构参数中的管路壁厚、折弯处与压缩机端部之间的管路长度、管路空间角和U形管的长度以及它们之间的交互作用对管路振动性能有显著影响;

(3)通过采用非劣质遗传算法(NSGA-II)对拟合的二阶响应面近似模型进行目标值寻优，研究结果表明，优化后的管路质量下降了27.21%，管路振动最大位移下降了76.5%，管路振动最大应力降低了86.73%，且管路的固有频率远离了压缩机的工作频率，大大降低了系统共振的可能性.研究结果表明通过试验设计对空调管路结构进行多参数和多目标优化设计是可行的.