匀变速运行轨道车辆非平稳随机振动分析

殷明娟，赵岩

(1. 大连交通大学 机械工程学院，辽宁 大连 116028；2. 大连理工大学 工程力学系，辽宁 大连 116023)*

车轨耦合振动是一类典型的动力学问题，由于轨道不平顺具有随机的本质，由其诱发的轨道车辆振动具有显著的随机振动特征，并显著影响列车的运行舒适性和疲劳可靠性[1-3].车辆轨道耦合系统振动的频率成份与轨道不平顺波长和车辆行驶速度密切相关.车辆行驶速度在很多文献中被假设为一个常量，这对于轨道车辆平稳运行分析是恰当的.而实际轨道车辆运行必然经过加速或减速过程，此时由于速度的变化，轨道车辆的随机振动成为非平稳过程.在变速移动载荷对于结构振动行为的影响方面，Zibdeh等[4-5]研究了移动随机荷载作用下复合梁结构振动问题，讨论了载荷移动的速度效应和材料铺层的方向效应.Michaltsos等[6]采用常幅值、变速特征移动载荷模拟双轴车辆载荷，讨论了加速和减速等不同情形下结构动力学响应.Yin等[7]基于协方差等效原则研究了变速车辆作用下桥梁非平稳随机振动问题.

本文开展了匀变速运行轨道车辆非平稳随机振动研究.分别采用多刚体模型、三层离散点支撑有限元模型模拟车辆和轨道系统，并通过赫兹接触关系建立了车辆-轨道耦合运动学方程.在考虑轨道车辆匀变速运动过程中，提出从空间平稳轨道不平顺功率谱转换时域非平稳不平顺功率谱方法，能够在每一时间段内有效模拟速度的连续变化过程.考虑不同车轮多点完全相干效应，应用虚拟激励法将非平稳振动分析转换为确定性的时域逐步积分分析，通过构造适当的精细积分格式实现了有效的求解.

1 车轨耦合系统动力学方程

1.1 车辆动力学方程

考虑如图1所示车轨耦合系统，将车辆系统动能和势能分别表示为系统自由度的函数，考虑阻尼以及系统所受外载荷，可得相应的车辆系统运动方程

图1 车轨耦合系统

(1)

其中，[Cv]为车辆系统的阻尼阵；{p}为车辆系统的外载荷向量；[Ev]为作用力指示矩阵.

1.2 轨道系统动力学方程

轨道系统采用三层离散点支撑模型，钢轨服从Euler梁假定，采用有限元进行轨道模型离散，可得轨道系统动力学方程

(2)

1.3 车轨耦合系统运动方程

通过轮轨关系建立车轨耦合系统运动方程，假设车轮与弹性轨道之间的相互作用按线性赫兹理论连接.对于图1所示的车轨耦合系统动力学模型，4个耦合接触力可表示为

pi=kh(uti+ri-uwi),i=1,2,3,4

(3)

其中，khutiuwi和ri分别为接触刚度、接触点轨道位移、车轮位移和轨道不平顺.轮轨接触点轨道位移uti由形函数分解得到.

基于式(3)给出的耦合力边界条件，可以得到车辆与轨道耦合系统动力学方程

(4)

2 车轨耦合系统非平稳随机振动

2.1 匀变速行驶下演变轨道不平顺谱

假设轨道不平顺r(x)为以空间坐标为自变量的零均值平稳随机过程，其相应的以空间圆频率Ω为自变量的自功率谱密度函数Sr(Ω)已知.通过速度与位移之间关系式x=vt可以将随机轨道不平顺由空间域转换到时间域r(t).在t∈[t0,t0+Δt]的区间内，假定列车匀变速v(t)=v0+at行驶，其中v0为初速度，a为常加速度.利用一阶摄动可以得到匀变速运动情形下轨道功率谱St.

2.2 车轨耦合系统非平稳随机振动分析

方程(4)可以应用Newmark方法等进行时域逐步积分计算，但精细积分方法具有一定优势，对于线性、多项式、三角函数等类型载荷，可以获得高精度数值解[8-9].下面建立匀变速行驶下车轨耦合系统时域分析的精细积分格式，将运动方程(4)表示成状态空间形式

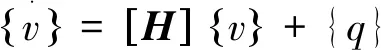
(5)

假定已知tk时刻车轨耦合系统的状态向量为{v(tk)}，则在tk+1=tk+Δt时刻，系统的状态向量{v(tk+1)}可以按下式进行计算

(6)

其中，[T(Δt)]=exp([H]Δt)是指数函数矩阵，{vp(t)}是特解向量.

给出特解{vp(t)}的推导，方程的外载荷向量为

(7)

在t∈[tk,tk+1]时间内，考虑四个接触轮位置轨道不平顺的相干效应，基于虚拟激励法构造匀变速虚拟轨道不平顺

(8)

其中，ti(i=1,2,3,4)为不同车轮之间轨道不平顺作用的滞后时间，g(ω,vtk,t)为调制项.

将虚拟轨道不平顺(8)代入方程(7)，得到

(9)

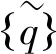
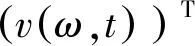
(10)

由功率谱密度响应，进一步可计算响应的时变标准差.

3 数值算例

3.1 方法验证

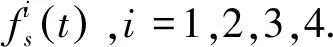
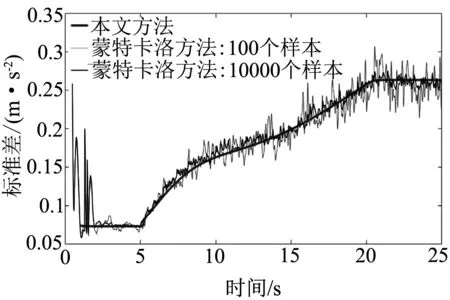
图2 车体垂向加速度响应对比

假定列车为匀加速运动，加速度为3.89 m/s2.初始速度为50 km/h，匀速行驶5 s，之后加速行驶15 s，速度达到260 km/h，再匀速行驶5s.图2给出了Mote Carlo方法与本文提出方法进行变速运动下车体垂向自由度非平稳标准差响应的对比验证结果.其中蒙特卡罗方法分别计算了100个样本和10 000个样本.从图中可以看到对于100个样本的蒙特卡罗方法存在一定跳跃偏离，而对于10000个样本的蒙特卡罗方法与本文给出的随机振动方法计算结果符合非常一致，验证了本文方法的正确性.

3.2 匀变速过程演变功率谱响应

分析频率区间为fl=0.1，fu=10，采用50个分析频点.初始速度为50 km/h，进行匀加速运动，加速度分别为2.41 m/s2，0.56 m/s2，最终运行速度达到180 km/h.采用本文分析方法进行上述匀变速情况车辆非平稳随机振动分析.计算结果如图3所示.图3(a)和3(b)分别为加速度等于2.41 m/s2和0.56 m/s2时车体垂向加速度功率谱响应计算结果，从图中可以看出随着时间的变化功率谱的形状与峰值都发生相应的变化.当加速度比较小时，功率谱响应单位时间的变化会更平稳；而加速度比较大时，功率谱响应单位时间的变化会增大.

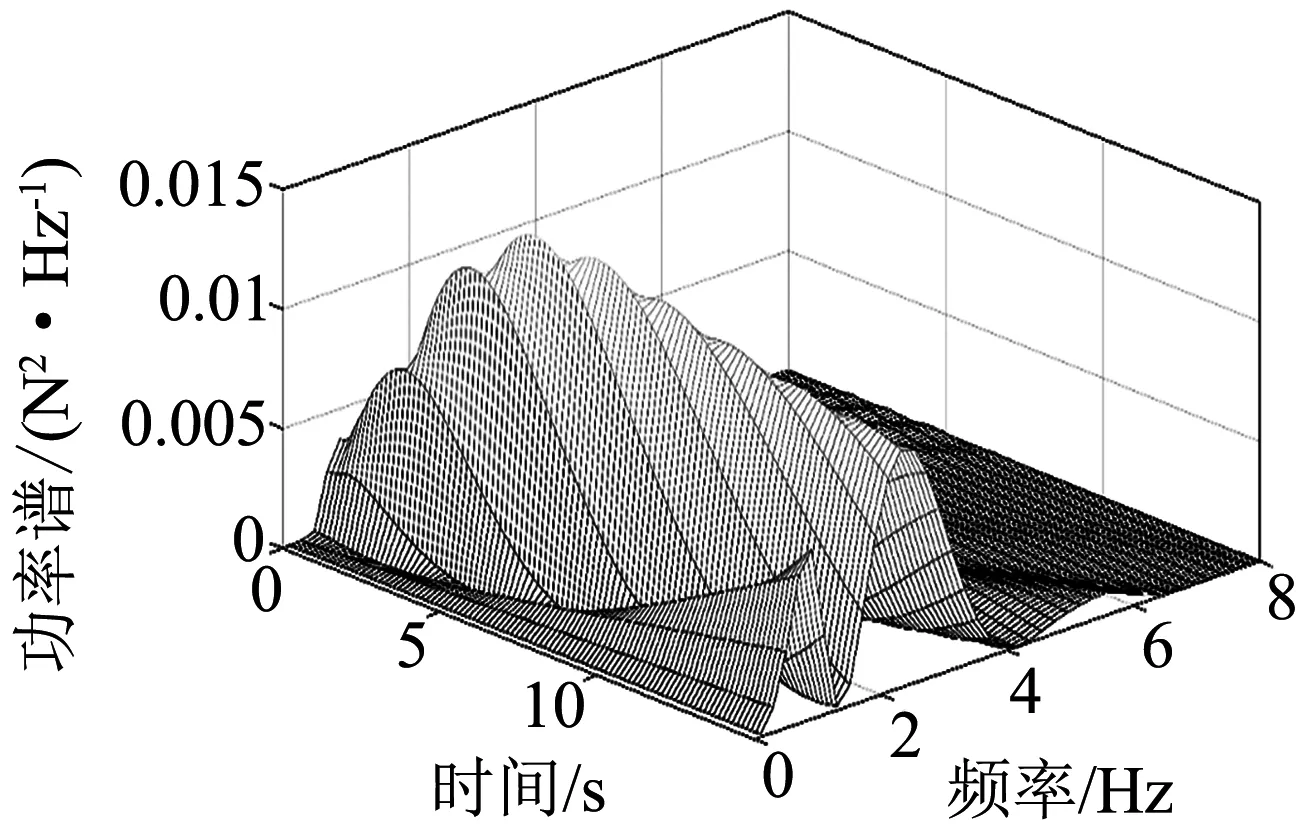
(a) 加速度为2.41 m/s2

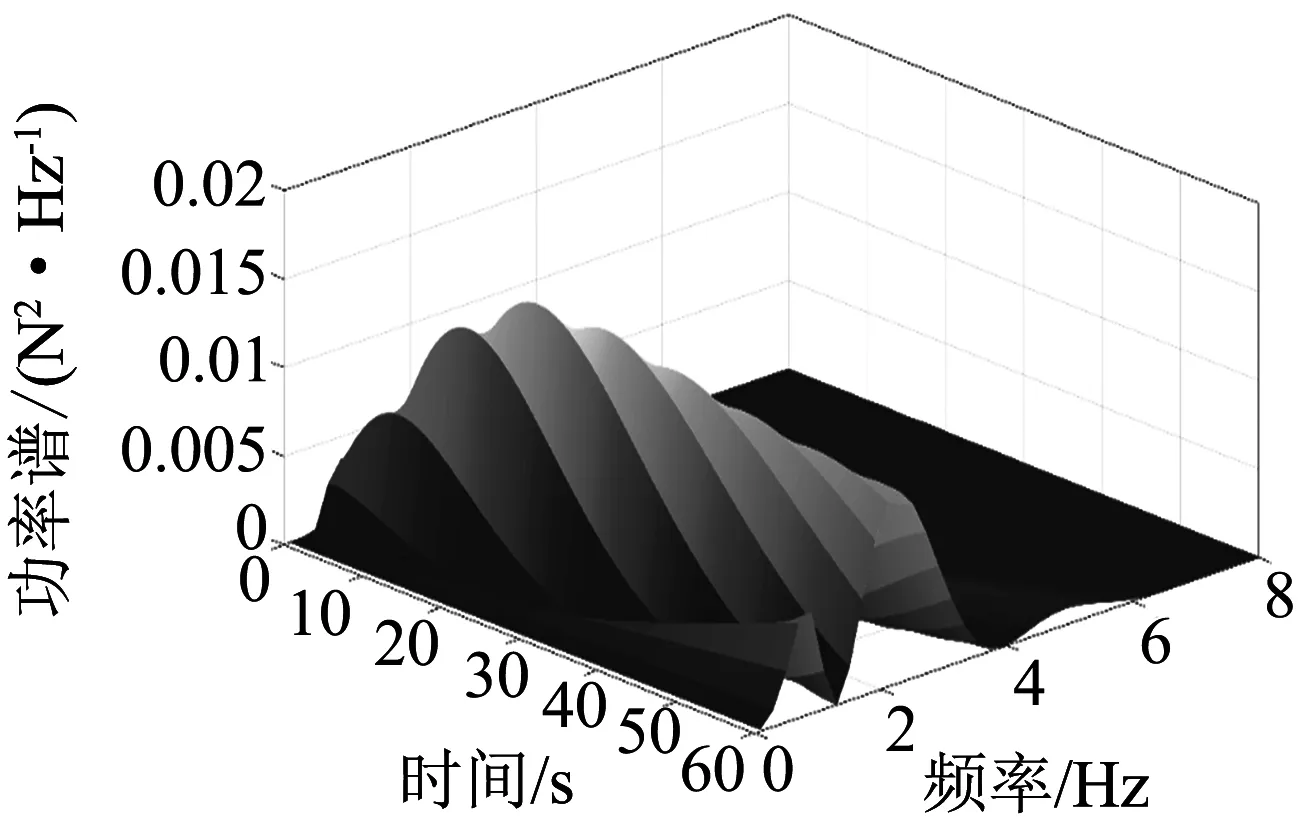
(b) 加速度为0.56 m/s2图3 车体垂向加速度功率谱

3.3 轮轨激励的完全相干特性

列车在轨道上行驶受到轨道不平顺的激励，4个车轮所受激励都具有同样载荷作用特性，也即激励之间是完全相干的，但存在相位差的载荷作用特性.假定分析频率区间为fl=0.1，fu=10，采用50个频点.进行匀加速度运动，加速度为1 m/s2；初始速度为5 km/h，最终速度为20 km/h.从图4中可以看出功率谱在时-频空间分布更为复杂，出现了无规律分布的多个峰值.假定车轮1和车轮2为第一组，车轮3和车轮4为第二组.如果两组所受激励是同向的，则车体垂向响应会出现波峰；如果两组所受激励是反向的，则车体垂向响应会出现波谷.同向激励情况的激励相位相差为2kπ,k=1,2,…,n；反向激励情况的激励相位相差为(2k+1)π,k=1,2,…,n.

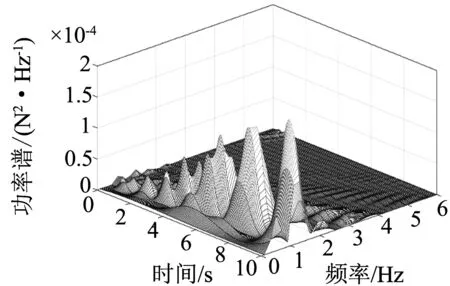
图4 完全相干效应对车体垂向响应的影响

4 结论

本文建立了轨道不平顺作用下匀变速运动情形车轨耦合系统的非平稳随机振动分析方法.采用刚体车辆动力学模型与离散点支撑轨道有限元模型相互耦合的动力学系统进行了随机振动响应分析，计算结果与Mote Carlo方法对比，表明所建立的方法正确性.匀加速运动情形车辆非平稳随机振动分析表明，随着时间的变化功率谱的形状与峰值都发生相应的变化.分析了车轮所受激励的相干特性，该特性是形成时-频空间功率谱分布复杂性的一个主要原因.这些工作为进一步采用更为精细的弹性体模型模拟实际车辆系统，并进行变速情形下系统的动力学行为特征分析打下了一定的基础.