带有Smith增长率的计算机网络蠕虫传播模型研究

施键兰，李英国

(1.福州工商学院工学院，福建 福州 350715;2.福建师范大学数学与信息学院，福建 福州 350117)

0 引 言

如今计算机网络和人们的日常生活联系得越来越紧密。在给人们带来便利的同时，计算机网络也面临着各种各样的威胁。 随着计算机的广泛应用，人们开始关注与计算机相关的网络安全问题。 在众多威胁网络安全的技术中，网络蠕虫作为一种特殊的计算机程序实现技术，对计算机网络系统具有巨大的潜在威胁。 网络蠕虫是程序员插入计算机程序中的一组指令或程序代码。 这些指令或程序代码破坏计算机网络的功能或数据，可能影响计算机网络的使用，并可能自行复制。 计算机网络蠕虫是一种典型的试图连接到主机并主要通过网络传播到其他计算机的程序。 感染是网络蠕虫威胁的主要特征之一。 网络蠕虫感染不仅提高了网络蠕虫的生存率，而且对网络资源造成了破坏和威胁。 随着计算机网络的发展，网络蠕虫越来越流行，网络蠕虫的威胁越来越严重，反网络蠕虫的任务也越来越艰巨。 因此，了解控制计算机网络蠕虫传播的规律是很有意义的。

通过数学建模方法，建立动力学模型分析计算机网络蠕虫的工作开始于20世纪90年代初期，有学者考虑到网络蠕虫和生物流行病毒的相似性，利用其与生物流行病类似的建模方式来建立计算机网络蠕虫模型，并且分析计算机网络蠕虫模型的动力学行为，为以后计算机网络蠕虫的建模和研究奠定了基础。 历经几十年, 网络蠕虫模型的研究已经逐步走向成熟，模型的研究方法也不断完善。 通过建立数学模型探究网络蠕虫的传播规律，这是目前最常用的研究途径。 根据计算机网络蠕虫的传播机制，结合网络蠕虫的传播特点，建立并研究新的网络蠕虫传播模型以及网络蠕虫模型的分析仍然有许多工作需要进一步考虑,为计算机网络蠕虫防控提供了很好的理论支撑。

现实生活中，计算机网络蠕虫传播系统的演化过程中，有时会使得计算机网络蠕虫传播系统的稳定性发生翻转，对于计算机网络蠕虫传播模型而言，一旦系统失去稳定状态，会进一步导致系统崩溃，可能造成难以估计的有害影响。 对于微分方程描述的网络系统，有研究指出，当系统网络受到恶意软件攻击，受感染节点的稳定性发生变化时，网络利用率下降，并且引起网络性能下降，会严重阻碍网络的正常运行。 因此，研究网络蠕虫的传播模型，对于网络优化和网络安全课题显得非常迫切和重要。 这不仅在理论上很重要，在工程应用中也很重要。

近年来，许多学者开始关注计算机网络蠕虫传播模型动力学行为影响，得到了一些比较好的结果。 文献[1]借助生物学领域已有的数学模型来对计算机网络蠕虫进行研究,提出经典的SIR网络蠕虫模型。 在此基础上，不少学者对计算机网络蠕虫传播模型加以改进并进行研究。 文献[2]提出了计算机网络蠕虫传播的非线性和线性模型，给出了非线性和线性模型中无蠕虫平衡点全局稳定性的充分条件。 文献[3]研究了一类具有非连续免疫策略的计算机网络蠕虫模型，证明了模型平衡点的存在唯一性。 文献[4]提出了网络蠕虫在潜在机制下的传播模型，论证了网络蠕虫传播平衡点的局部稳定性。文献[5]研究了一个具有密度依赖和有限抗蠕虫能力的计算机网络蠕虫模型，分析了系统平衡点的局部稳定性和存在性。 文献[6]建立了基于隔离潜伏机制的网络蠕虫模型，并应用数学工具证明了系统平衡点的局部稳定性。文献[7]建立了基于复杂网络理论的一个网络蠕虫传播模型，分析了模型平衡点的稳定性。文献[8]建立了新的网络蠕虫传播模型。 研究了网络蠕虫的传播规律。 文献[9]利用非线性微分动力学系统研究了网络蠕虫的局部稳定性等传播动力学行为。 文献[10]提出了具有抗蠕虫能力的计算机网络蠕虫传播模型，并且研究了模型平衡点的稳定性。

Logistic模型是假定网络计算机数量的相对增长率是网络计算机数量成正比的基础上而建立的，Smith模型是假定网络计算机数量的相对增长率由于网络资源的限制与该时刻网络的剩余资源成正比，根据文献[11]，由于Logistic增长率不如Smith增长率符合实际中的计算机网络增长情形，本文在文献[10]基础上，提出了一种连接到网络的外部计算机数量符合Smith增长率的计算机网络蠕虫传播模型。

1 模型建立

如果把网络中一台路由器或计算机主机当成一个节点。 节点分为免疫节点、感染节点与易感节点。 以R(t)表示时刻t的计算机网络免疫节点数；I(t)表示时刻t的计算机网络感染节点数；S(t)表示时刻t的计算机网络易感节点数。 基于以上假设，文献[1]建立以下SIR计算机网络蠕虫传播动力学模型：

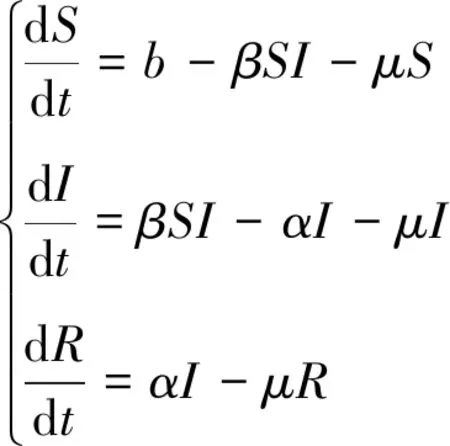
(1)

其中，b表示外部计算机接入到网络的速率，β表示计算机网络感染节点与易感节点的感染率系数，μ表示计算机网络节点的自然淘汰系数，α表示计算机网络节点的免疫状态返回到易感状态的概率。

在此基础上，文献[10]考虑了外部连接到网络的计算机数量符合Logistic增长率的SIR计算机网络蠕虫传播动力学模型：

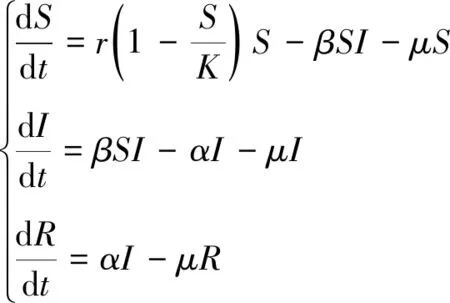
(2)

其中，K表示最大化的网络容量，其余参数的含义同系统(1)，其中r>μ。

由于Logistic增长率不如Smith增长率符合实际中的计算机网络增长情形，本文提出了一种更通用的计算机网络蠕虫传播模型，其中连接到网络的外部计算机数量符合Smith增长率：

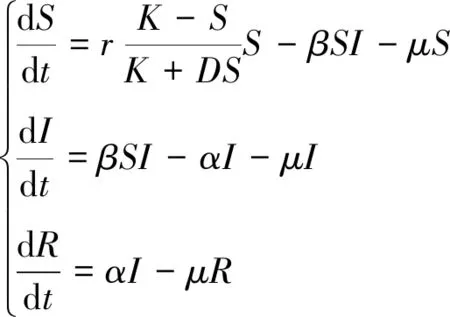
(3)

D是一个比例系数，它表示网络中由于资源的限制造成的对计算机节点增长的影响。 当参数D>0时，节点数量具有Smith增长率，当D=0时，系统(3)退化为系统(2)。

由于系统(3)前两个方程不包含R变量，所以可以考虑如下系统：

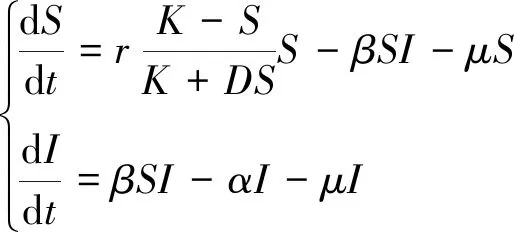
(4)

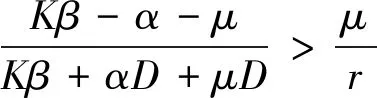
2 稳定性分析

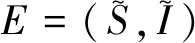
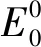
(λ-r+μ)(λ+α+μ)=0，

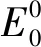
定理2

证明系统(4)在E0处的特征方程为

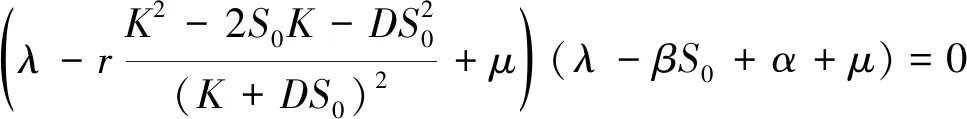
(5)

解得

定理3

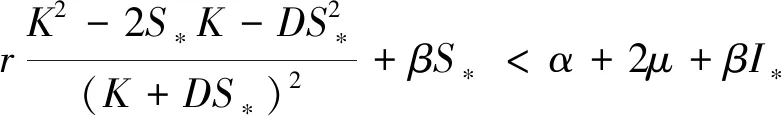
证明系统(4)在E*处的特征方程为

(6)

解得

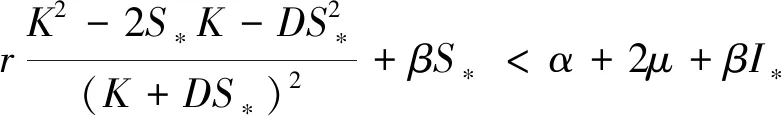
3 数值模拟

由于地方病平衡点在计算机网络系统中非常重要，在本节中，为了验证定理3的正确性，对式(4)进行数值模拟如下：取K=100，r=2，D=β=μ=α=1，根据定理3，得到地方病平衡点渐近稳定，具体情形如图1，图2所示。

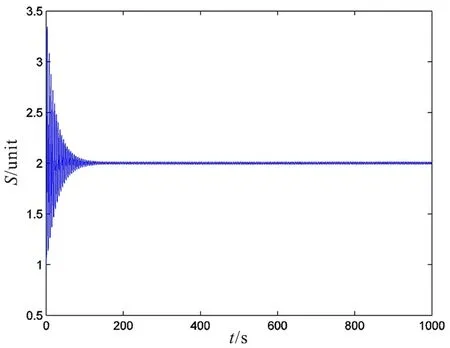
图1 地方病平衡点数值仿真t-S平面Fig.1 t-S plane numerical simulation of endemic disease equilibrium point

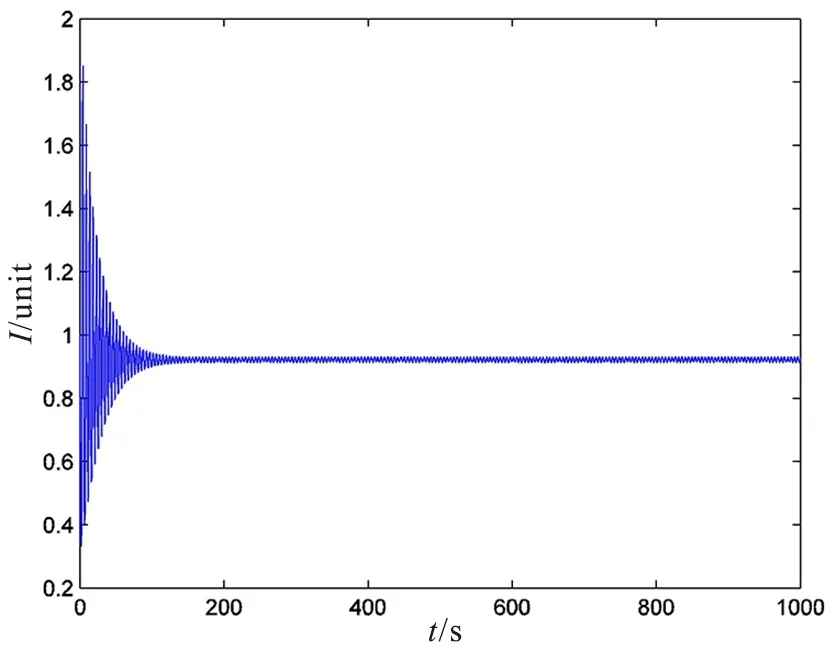
图2 地方病平衡点数值仿真t-I平面Fig.2 t-I plane numerical simulation of endemic disease equilibrium point

4 结语

计算机网络蠕虫的防治是网络安全领域的一项重要课题，是一项复杂而长期的任务，有必要深入研究计算机网络蠕虫的传播原理，为有效防治计算机网络蠕虫提供理论依据。 本文在前人研究工作的基础上提出了一种带Smith增长率的计算机网络蠕虫传播模型。 讨论了平衡点的稳定性，上述研究结果对网络蠕虫的预防和网络环境的优化具有重要的理论意义。

为了评估本文的网络蠕虫传播模型在现实计算机网络中的有效性，有必要收集大量的网络数据进行估算，对模型中涉及的参数进行统计分析，从而预测网络的理论动力学行为，并观察网络的实际动力学行为。如果网络的实际动力学行为符合本文的预测，模型是有效的。除此之外，本文的模型还需要进一步的修改和分析来适应现实网络，比如考虑时滞因素，分析模型中的霍夫分岔动力学行为，即周期震荡行为，设计控制方法把不稳定的网络平衡点变为稳定等等，以上是下一步的研究目标。