基于T-S模糊神经网络模型求解Black-Scholes方程

2021-05-20袁亚蕊李战辉

闽江学院学报 2021年2期

袁亚蕊，李战辉

(1.集美大学诚毅学院，福建厦门 361021;2.阿里巴巴网络技术有限公司，浙江杭州310000)

0 引言

1973年，Black和Scholes提出了经济和金融市场中著名的随机偏微分方程Black-Scholes方程[1]。它通过构建标的资产当前市场价格和到期日之前剩余时间的函数求解期权的价格。Black-Scholes方程背后的基本思想是，对给定资产的投资可以对冲卖出或购买适当数量的期权。利用Black-Scholes方程进行期权定价时，对方程的求解一直是难点问题。目前，关于Black-Scholes方程解的相关研究大多采用数值法。Andalaft等用有限元方法得到了实物期权定价问题的解[2]。Fadugba等提出了期权定价的Crank-Nicolson有限差分法来求解Black-Scholes方程[3]。甘小艇等将美式看跌期权问题简化为与之等价的变系数抛物型方程，构造了两个全离散二次有限体积格式并验证其解的存在唯一性[4]。Rad等提出使用径向基点插值方法(RBPI)求解Black-Scholes方程[5]。吴蓓蓓等研究了Black-Scholes欧式期权定价模型的三次三角B-样条配点法[6]。Cervera等利用人工神经网络求解Black-Scholes方程[7]。

模糊神经网络技术利用神经网络理论，通过处理数据来确定其性质(模糊集和模糊规则)。模糊神经网络模型汇集了模糊理论与神经网络模型的优点，既具有神经网络的学习能力和计算能力，又具有模糊系统的优势。神经网络模型已经成功地应用于从图像识别、语音识别、时间序列分析到偏微分方程的数值逼近等一系列问题的数值拟合。这种数值拟合应用表明，模糊神经网络模型可以有效的对复杂函数进行逼近，对训练样本的要求比较低。其中，T-S模糊神经网络模型结合了神经网络自适应能力和模糊逻辑定性方法，具有较强的逼近拟合能力。本研究利用T-S模糊神经网络模型的逼近能力，在Cervera等人的神经网络模型的基础上，提出一种更高效的求解Black-Scholes方程的方法，即采用T-S模糊神经网络模型求解Black-Scholes方程并通过数值拟合验证该方法的有效性。

1 基本模型

1.1 Black-Scholes方程

本文用T表示到期日，St(0≤St<+∞)表示在t(0≤t≤T)时刻股票价格，F(t,St)表示在t时刻股票期权的价格，K表示执行价格，r表示无风险利率，σ表示波动率，那么Black-Scholes方程可以表示为：

(1)

在使用方程(1)进行期权定价时，虽很难求出解析解，但可以根据具体的边界条件求出方程的解析解或数值解。对于欧式看涨期权，方程的边界条件为F(T,St)=max(ST-K,0)；对于欧式看跌期权，方程的边界条件为F(T,St)=max(0,K-ST)[8]。方程在这两种情况下都有显式解，且求解过程相似，避免重复，本研究以欧式看涨期权为例。当边界条件为F(T,St)=max(ST-K,0)时，求解方程(1)，可以得到：

F(t,St)=StN(d1)-Ke-r(T-t)N(d2),

(2)

这里

(3)

(4)

1.2 T-S模糊神经网络模型

T-S模糊神经网络模型能不断修正模糊子集的隶属函数，具有很强的自适应能力。本研究使用的T-S模糊神经网络模型是由前件网络和后件网络组成，其网络结构如图1所示。

图1 T-S模糊神经网络模型的网络结构Fig.1 The network structure of T-S fuzzy neural network model

T-S模糊神经网络模型的前件网络有4层。第一层为输入层，节点数和输入向量的维数相同，该层有n个结点。第二层是计算隶属度函数，第三层是运算出模糊规则的适用度，第四层进行归一化运算。

在第二层，对于输入量x=[x1,x2,…,xn]′，根据模糊规则计算各输入变量xi的隶属度函数：

(5)

在第三层，将各隶属度进行计算，使用模糊算子为连乘算子：

(6)

在式(6)中，

在这一层，结点总数为m。

在第四层，结点总数也为m，可以实现归一化运算：

(7)

T-S模糊神经网络模型的后件网络由r个并列子网络构成，这些子网络结构相同且均运算出一个输出量。子网络有3层，第一层为输入层，第二层可运算出模糊规则的后件，第三层为输出层。

在子网络第二层有m个结点，每个结点有一条规则，可以对每条规则的后件进行运算，即：

(8)

在子网络第三层，可以运算出输出值yi：

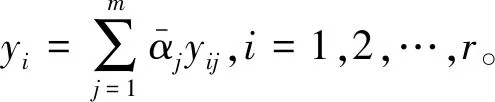
(9)

2 采用T-S模糊神经网络模型求解Black-Scholes方程的框架

为了计算Black-Scholes方程的解，将求解区域划分为均匀网格。考虑在离散的网格点(ti,Sj)(i=1,2,…,Nt,j=1,2,…,NS)满足方程(1)，则原问题可以转化为

(10)

(11)

式(2)中欧式看涨期权的价格用Ca来表示。为了评价T-S模糊神经网络的逼近效果，给出如下误差函数：

(12)

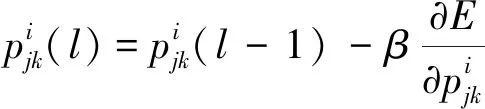
(13)

在式(13)中，β为T-S模糊神经网络模型的学习率。

T-S模糊神经网络模型参数diji和biji的修正：

(14)

(15)

3 数值实例

将求解区域划分为均匀网格,Nt=NS=11,21,31。在离散的网格点上，根据适当的边界条件，K=10,r=0.1，σ=0.4,0≤T-t≤1，0≤St≤45，对欧式看涨期权的Black-Scholes方程求解。输入数据的维数为2，模型输出数据的维数为1，设定隶属度函数个数为4。首先根据式(5)中的隶属度函数计算输入变量的隶属度，模糊规则计算采用式(6)计算得到αj，接着利用式(7)进行归一化运算，再采用式(8)、式(9)计算出T-S模糊神经网络模型的输出值。系数和参数采用式(13)～式(15)进行修正。经过模糊神经网络计算，最终得到了很好的Black-Scholes方程的近似解。

由图2、图3可知，网格每个方向等分点(Nt=NS=11)相同时，随着迭代次数1 000增加至10 000，误差函数的值呈下降状态。由图3可知，Nt=NS=11,21,31时，即网格点数增加，迭代10 000次，误差函数的值从小于0.1减小到0.01左右，呈下降状态。文献[7]的神经网络法在Nt=NS=11,21,31时，迭代10 000次，误差均在0.1左右。在图3中，T-S模糊神经网络模型求解Black-Scholes方程使用的等分点数、迭代次数与文献[7]中神经网络法相等时，误差函数的值却小于文献[7]中神经网络法。在图2中，当迭代次数为1 000时，误差函数的值就达到了0.1。可见本研究使用T-S模糊神经网络模型的结果精度高，收敛速度快。