非均质土中海上风电单桩基础动力响应特性
2021-05-19孔德森邓美旭李亚洲
孔德森,刘 一,邓美旭,李亚洲
1) 山东科技大学山东省土木工程防灾减灾重点实验室,青岛 266590 2) 山东科技大学大学土木工程与建筑学院,青岛 266590 3) 中铁建工集团山东有限公司,青岛 266100
风能源已经逐渐成为取代传统能源发电的一种主要形式,具有无污染、可再生等特点,是一种取之不尽、用之不竭的新能源[1]. 我国具有漫长的海岸线,近海资源丰富,空间区域广阔,海上风电场逐渐成为风力发电的开发重点[2−3]. 大直径单桩基础由于其制作与安装方便快捷、相对于群桩而言受力条件明确、造价经济等优势,在海上发电领域得到了广泛应用[4]. 大直径单桩基础在服役期间内受到来自风、洋流、波浪等水平荷载的作用,其水平循环受荷特性显著[5]. 研究大直径单桩基础在水平循环荷载下的动力响应特性,对于消除安装工程中的隐患,保证服役期间正常使用均具有重要意义.
关于水平循环荷载下单桩基础动力响应特性,国内外学者进行了相关研究,并且取得了一定的成果. Leblanc等[6]和Peng等[7]利用离心试验研究循环次数、桩径、荷载大小以及砂土密实度对模型桩侧向位移的影响. 郭鹏飞等[8]基于非饱和土的动力控制方程,考虑横向惯性效应,建立了三相非饱和介质中桩的竖向动力响应连续介质模型,得到了桩侧土体剪应力及竖向振动位移的表达式. 张光建[9]对ABAQUS进行二次开发建立土体刚度衰减模型,重点研究了不同影响因素下大直径单桩基础水平位移的发展趋势. Basack与Banerjee[10]基于数值模型研究了层状土中桩基础在横向荷载作用下的响应,同时利用现场试验数据对模型进行了验证,并进行了参数化研究.Bhattacharya与Adhikari[11]对桩‒土相互作用进行了实验研究,结果表明,考虑桩‒土相互作用时设计出的基础结构使用寿命更长. 朱斌等[12]研究了砂土中大直径单桩离心模型试验结果,定义了临界循环应力比,给出了其与循环折减系数的关系.Kuo等[13]和Achmus等[14]建立了砂土的循环刚度衰减模型,得到了桩‒土体系在N次循环后的承载变形特性. 但是对于水平循环荷载作用下非均质土中海上风电单桩基础动力响应特性的研究比较少.
本文以海上风电单桩基础为研究对象,采用有限元分析软件ABAQUS建立了非均质土中海上风电单桩基础数值计算模型进行研究,在模型中将桩基础受到的波浪、洋流、风荷载等效成双向对称循环荷载,对水平循环荷载作用下桩身水平位移、桩身剪力、桩身弯矩、桩内外壁土抗力沿埋深变化特性进行了研究,并对不同循环次数下桩身水平位移进行了对比分析.
1 数值计算模型的建立
1.1 模型概况
以我国东海某近海海域风电场为例,建立了非均质土中海上风电单桩基础数值计算模型,由于荷载和结构的对称性,选择半个物理模型的桩土体系进行建模,数值模型为半圆柱体. 为了忽略边界条件对桩土体系的影响,在几何模型上,用大尺寸来模拟半无限空间体,土体直径取20D (D为桩径),土体高度取2hem(hem为桩的嵌固深度),该尺度可满足最小边界尺寸和计算精度的要求[15−16].
ABAQUS中通过桩‒土表面定义接触属性以模拟桩与土之间的剪力传递和相对位移,采用主‒从接触算法,选择刚度大的桩体为主控面,土体表面为从属面,桩‒土法向行为采用硬接触,切向行为采用摩尔‒库伦摩擦罚函数形式,界面滑动摩擦系数选取为土体内摩擦角)[17],接触对采用面对面接触与有限滑移. 边界条件是约束断面处y方向位移,约束模型侧面x和y方向位移,模型底端为固定约束. 桩体和土体都采用8节点6面体线性减缩积分三维实体单元(C3D8R),采用扫掠的方式对网格进行划分,从而使网格更加合理. 为了减小计算误差,同时也为了缩短计算时间,采用为边布种的方式,在桩土接触面附近单元网格划分得较细,而在远离接触面的土体,网格划分的相对稀疏. 在实际状况中,假定海床泥面处位移为零,土体内部是有应力存在的,因此在施加水平荷载前必须进行初始地应力平衡[18−19]. 本文采用ODB导入法进行初始地应力的平衡. 非均质土中海上风电单桩基础数值计算模型如图1所示.

图1 非均质土中海上风电单桩基础数值计算模型Fig.1 Numerical model of offshore wind power monopile foundation in heterogeneous soil
为了模拟桩‒土之间的非线性,根据土层性质采用基于Mohr-Coulomb破坏准侧的理想弹塑性本构模型来模拟,孔位学等[20]认为在非关联流动法则条件下采用剪胀角 ψ =φ/2所得到的滑移线场与Prandtl理论一致. 桩周土及桩端土参数列于表1.桩体采用线弹性模型来模拟,桩的物理力学参数列于表2,其中15 m位于水中,1 m位于水面之上.

表1 桩周土及桩端土参数Table 1 Parameters of soil around pile and soil at pile end

表2 桩的物理力学参数Table 2 Physical and mechanical parameters of pile
1.2 荷载的确定与施加
为了建模方便和获得较强的规律性,采用的分析步为静力通用分析步,将海上风电单桩基础在工作期间受到的波浪、洋流、风等荷载等效成双向对称循环荷载[21−23]的形式来模拟非均质土中海上风电单桩基础动力响应特性,在模型中沿x轴方向不断循环加载. ABAQUS中采用周期型幅值曲线来定义水平循环荷载[24],周期型幅值曲线用傅里叶(Fourier)级数表示.
t≥t0时,幅值表达式为:
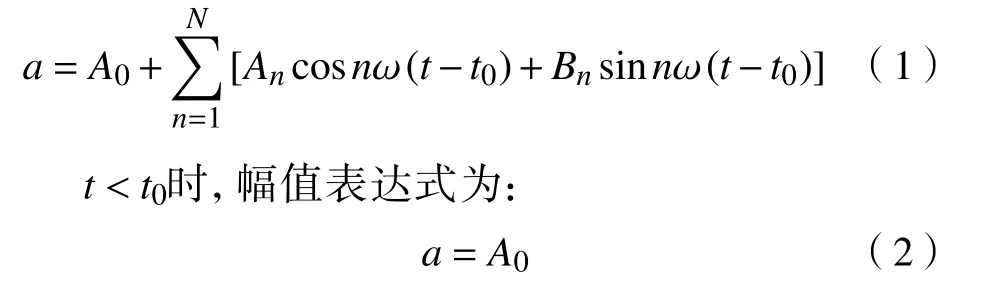
式中: ω 为圆频率,其值为 ω =2πf,f为 频率,t0为起始时间,A0为初始幅值,An为cos项的系数(n=1,2,3 , ···,N),Bn为 sin 项的系数.
1.3 桩侧土抗力分析
桩侧土抗力分布如图2所示. 由图(a)可知,水平荷载施加之前,初始土压力沿桩周均匀分布,初始有效压力值为 σ0. 荷载施加之后,土压力沿桩周分布形式出现了变化. 由图2(b)可知,施加水平荷载之后,桩周顺载侧有效土压力增大到 σmax,桩周逆载侧有效土压力减小至 σmin. 阴影部分Ⅰ区为桩周逆载侧减小的土抗力,阴影部分Ⅱ区为桩周顺载侧增加的土抗力. 施加水平荷载之后,作用在桩身的净土抗力Pnet为Ⅰ区和Ⅱ区之和[25−26].
2 数值计算结果分析
在模型中定义参考点,将参考点与水面处桩身横截面建立分布耦合约束,在参考点上施加水平循环荷载. 由于不同循环时桩身位移、桩身剪力、桩身弯矩和桩侧土抗力沿埋深随着时间的变化规律一致,循环的次数增加必然造成计算时间的增大,且对不同时间点的规律变化几乎无影响,循环次数较大时意义不大,为了节约计算时间,且不影响其规律分析,故本文对第20次循环时水平循环荷载作用下桩身位移、剪力、弯矩、桩内外壁土抗力沿埋深变化特性进行了研究,并对不同循环次数下桩身位移进行了对比分析.
2.1 水平极限承载力的确定
由于海上风机单桩基础桩径较大且采用钢管桩,桩身强度非常大[2],且桩的水平荷载‒位移曲线为缓变型,该曲线没有明显的拐点,可以认为是渐进式破坏,所以海上风机单桩基础的水平极限承载力主要由桩体的水平变形控制. 采用位移控制法,对桩顶施加0.3 m的水平位移,在有限元软件ABAQUS后处理中提取水平支反力和桩身水平位移的相关数据,然后利用绘图软件Origin绘制水平支反力与水平位移之间的关系曲线,得到桩顶荷载位移曲线,如图3所示.

图3 桩顶荷载位移曲线图Fig.3 Load‒displacement curve of pile top
根据允许变形法[9],将桩顶水平位移达到0.02D时对应的水平荷载,确定为海上风机单桩基础的水平极限承载力. 根据荷载位移曲线,当位移为0.1 m时对应荷载1.31 MN,为了反映单桩基础所受的荷载水平,单桩上施加的水平循环荷载幅值的大小为其水平极限荷载Fu的一定比值,为了避免荷载幅值过小或过大对分析结果造成影响,故取水平荷载幅值为0.6Fu,根据工程资料,荷载频率取为0.1 Hz进行研究.
2.2 桩身位移
对第20次循环时前5 s和后5 s桩身位移沿埋深变化规律进行分析,第20次循环时桩身水平位移变化曲线如图4所示.
由图 4(a)可知,191~195 s泥面处桩身水平位移分别为 13.7、25.3、26.4、17.2和1.83 mm,随着时间的增加,位移先增加后减小,且位移增加的幅度越来越小,减小的幅度越来越大,由于荷载呈对数形式增加—荷载逐渐增大且增大的幅度逐渐减小,造成桩身位移增加幅度变小,193 s时桩身泥面处位移最大,屈曲现象最明显,由于193 s之后荷载呈指数形式减小—荷载逐渐减小且减小的幅度逐渐增大,故桩身位移减小幅度增加. 193 s时与192 s时荷载值相同,但泥面处位移值比192 s时增加了 1.1 mm,194 s时与 191 s时荷载值相同,泥面处位移值比191 s时增加了3.5 mm,正向卸载与正向加载相同荷载值下桩身位移增大,说明循环荷载作用下桩身位移是不断累积的,不同时间点的桩身位移零点位于泥面下32~34 m,桩绕桩身轴线上某一点转动,表现出刚柔桩的性质.
由图 4(b)可知,196~200 s泥面处桩身水平位移分别为−13.7、−25.7、−26.8、−17.5和−1.82 mm,由于荷载和结构的对称性,负向荷载与正向荷载作用时桩身位移规律一致,关于y轴大致呈对称分布;196~200 s时桩身位移零点主要位于泥面下34~36 m范围内,桩身位移零点相比正向加载时发生了下移,这可能是由于循环过程中桩周土体软化引起的.

图4 第 20 次循环时桩身水平位移变化曲线. (a)前 5 s;(b)后 5 sFig.4 Horizontal displacement variation curves along the pile shaft during the 20th cycle: (a) first 5 s; (b) next 5 s
2.3 桩身剪力
对第20次循环时前5 s和后5 s桩身剪力沿埋深变化规律进行分析,第20次循环时桩身剪力变化曲线如图5所示.

图5 第 20 次循环时桩身剪力变化曲线. (a)前 5 s;(b)后 5 sFig.5 Shear force variation curves along the pile shaft during the 20th cycle: (a) first 5 s; (b) next 5 s
由图5(a)可知,随着时间的增加,桩身剪力先增加后减小,且剪力增加的幅度越来越小,减小的幅度越来越大,193 s时泥面处桩身剪力最大,正向卸载与正向加载相比相同荷载值下剪力是增加的. 由于桩周土体的抵抗作用出现反向的剪力值,不同时间点的桩身剪力反弯点位于泥面下7~9 m范围内. 191~192 s为正向加载过程,桩身剪力零点下移,193~195 s为正向卸载过程,桩身剪力零点逐渐上移. 不同时间点的剪力沿x轴正方向最大值均位于泥面处,沿x轴负方向最大值均位于泥面以下31~32 m范围内,此范围内应适当的增加壁厚,提高抗剪强度.
由图5(b)可知,负向加载时桩身剪力曲线与正向加载时桩身剪力曲线关于y轴大致呈对称分布,规律类似.
2.4 桩身弯矩
对第20次循环时前5 s和后5 s桩身弯矩沿埋深变化规律进行分析,第20次循环时桩身弯矩变化曲线如图6所示.
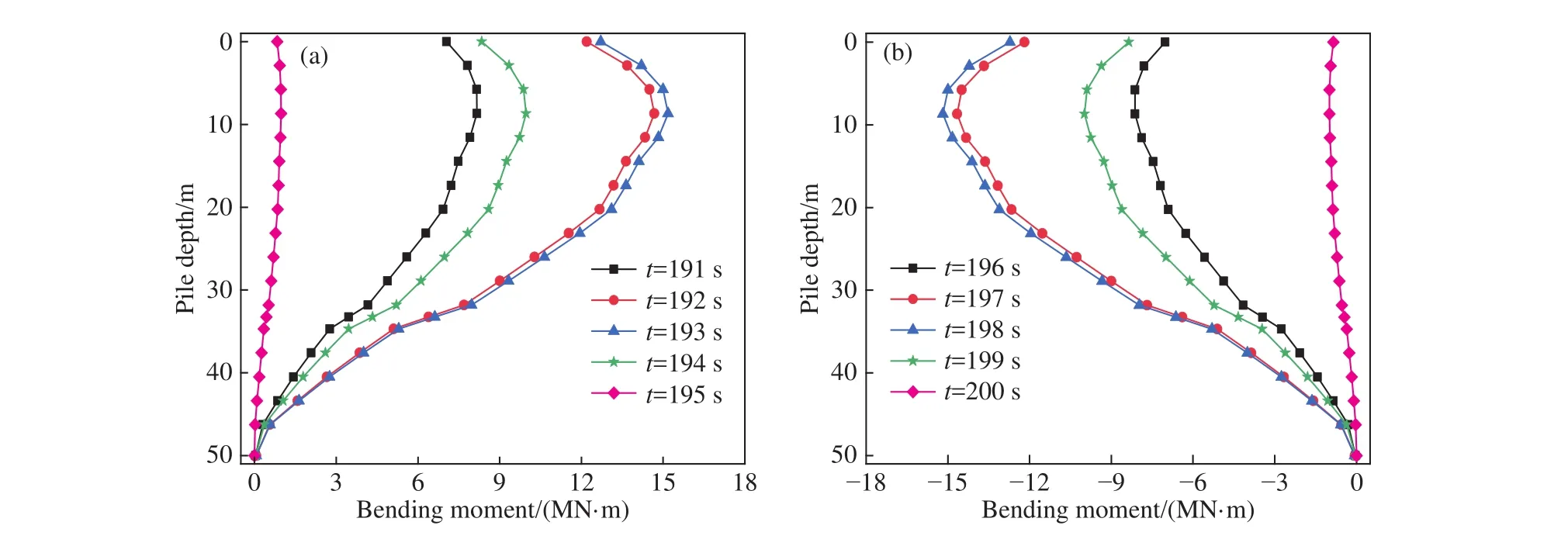
图6 第 20 次循环时桩身弯矩变化曲线. (a)前 5 s;(b)后 5 sFig.6 Bending moment variation curves along the pile shaft during the 20th cycle: (a) first 5 s; (b) next 5 s
由图6(a)可知,桩身弯矩由泥面处开始沿埋深先增大后减小,随着时间的增加,弯矩先增大后减小,且弯矩增加的幅度越来越小,减小的幅度越来越大. 不同时间点下桩身弯矩均没有出现反弯点,最大弯矩均位于泥面下7~9 m范围内,说明此范围内最容易发生破坏,在实际的工程设计时,此处桩身的壁厚或强度应适当增加,以减小桩体在该位置的转角. 随着时间的增加桩身最大弯矩对应的桩的埋深位置先增大后减小,与剪力零点表现出来的规律一致.
由图 6(b)可知,后 5 s桩身弯矩曲线与前 5 s关于y轴大致呈对称分布,规律类似.
2.5 桩侧土抗力
对第20次循环时前5 s和后5 s桩外壁土抗力沿埋深变化规律进行分析,第20次循环时桩外壁土抗力沿埋深分布曲线如图7所示.
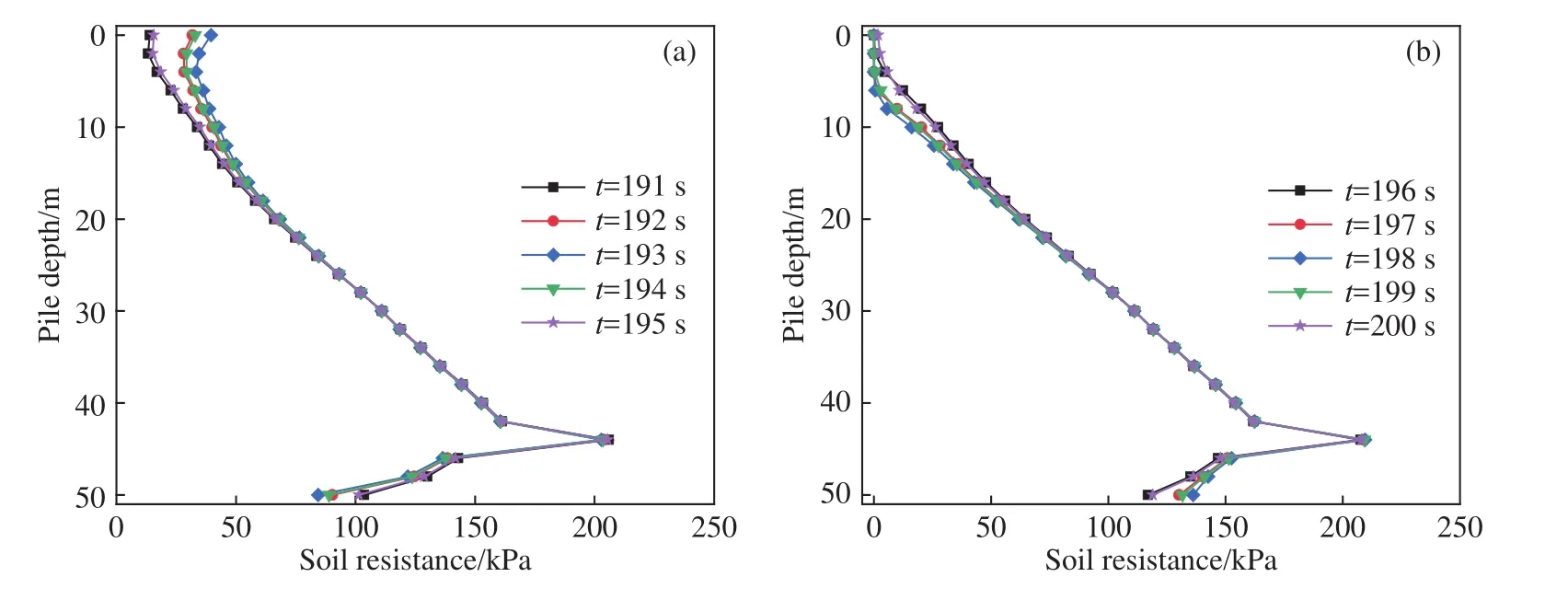
图7 第 20次循环时桩身外壁土抗力埋深分布曲线. (a)前 5 s顺载侧;(b)后 5 s逆载侧Fig.7 Soil resistance distribution curves of pile outer wall along the buried depth during the 20th cycle: (a) forward side of the first 5 s; (b) reverse load side after 5 s
由图7(a)可知,不同时间点桩顺载侧土抗力曲线随时间的变化存在分界点. 分界点以上桩侧土抗力随着时间的增加先增大后减小,这种变化主要集中在埋深20 m范围内,这是因为此范围内桩身位移为正,桩与外部土体相互挤压,桩外壁土压力为被动土压力;在193 s时达到最大,说明此范围内随时间的增加桩身承担荷载变化比较明显. 分界点以下桩侧土抗力随着时间的增加先减小后增大,这种变化主要集中在距桩底端4 m范围内,这是由于此范围内桩身位移为负,桩与外部土体产生分离的趋势,桩外壁土压力为主动土压力;在193 s时达到最小,说明此范围内随着时间的增加对桩侧土抗力影响较大. 在淤泥和粉砂土分界面处土抗力增加显著,究其原因,该处由于土层之间性质差异较大发生了明显的应力集中现象.
软黏土中桩外壁土抗力沿埋深逐渐增大,这是因为软黏土水平位移沿桩埋深逐渐增大,桩身需要提供较大的支撑力去约束较大的位移;而砂土中桩外壁土抗力沿埋深逐渐减小,究其原因,一方面是由于淤泥土层与粉砂土层相比土层性质较差,另一方面是由于淤泥土与粉砂土相比水平位移较大,且由于靠近桩端,粉砂土水平位移沿桩埋深逐渐减小,故桩身提供的支撑力沿埋深逐渐减小,表现为桩侧土抗力沿埋深逐渐降低. 桩外壁土抗力沿埋深变化不一致,说明桩顺载侧外壁土抗力的发挥不仅仅取决于桩土相对位移,还与埋深和桩侧土层性质有关.
由图7(b)可知,不同时间点桩侧土抗力发挥沿埋深不同,198 s时土抗力发挥位置埋深最大,这主要是因为此时桩身负向位移最大,与逆载侧土体脱离程度比较大,导致桩侧土抗力发挥沿埋深滞后. 不同时间点桩逆载侧土抗力沿埋深存在分界点,桩逆载侧土抗力随时间变化规律与顺载侧土抗力正好相反. 桩逆载侧土抗力沿埋深变化与桩身顺载侧外壁土抗力变化大致相同. 上部土层土抗力较小,下部土层土抗力较大,承担的荷载较大,可作为持力层.
对第20次循环时前5 s和后5 s桩内壁土抗力沿埋深变化规律进行分析,第20次循环时桩内壁土抗力沿埋深分布曲线如图8所示.
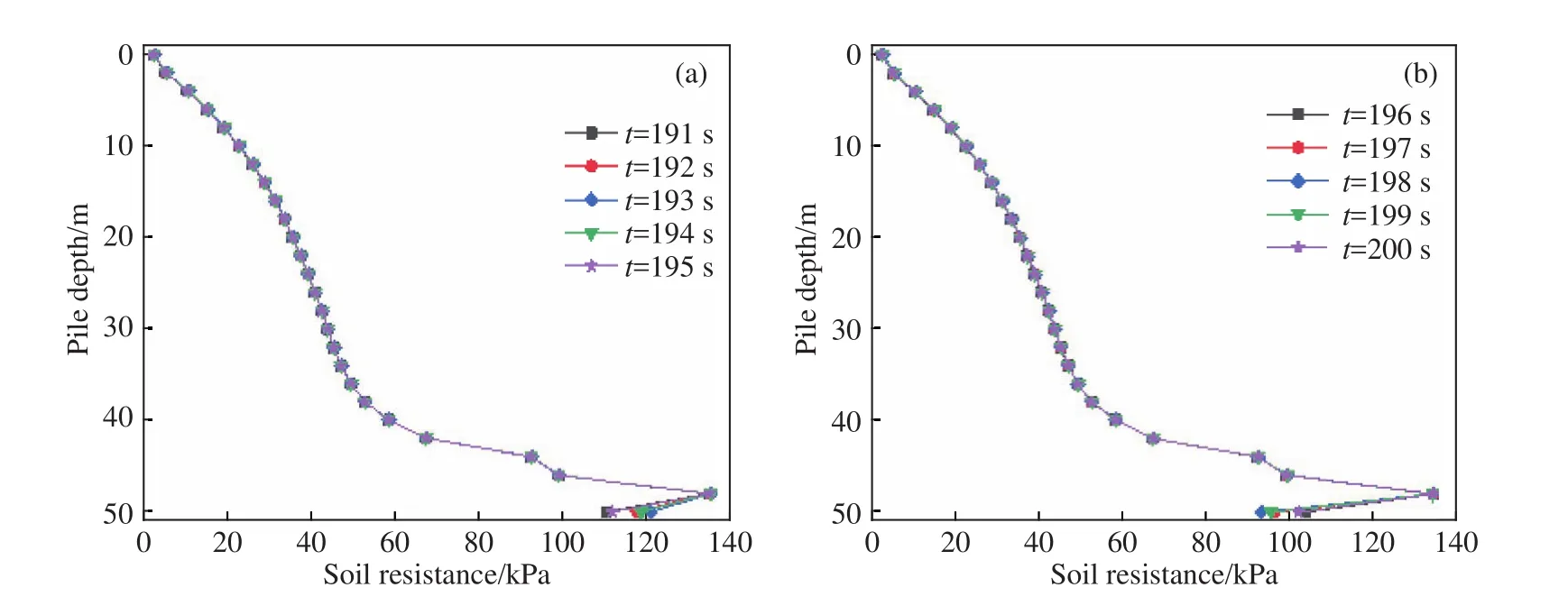
图8 第 20次循环时桩身内壁土抗力埋深分布曲线. (a)前 5 s顺载侧;(b)后 5 s逆载侧Fig.8 Soil resistance distribution curves of pile inner wall along the buried depth during the 20th cycle: (a) forward side of the first 5 s; (b) reverse load side after 5 s
由图 8(a)可知,191~195 s桩侧土抗力曲线沿埋深几乎重合,承担的荷载基本不变,在淤泥质黏土层中土抗力呈指数型增加,在淤泥土层中土抗力呈对数型增加. 粉砂土中土抗力先增大后减小,在距桩底端1/3粉砂土层层厚处土抗力值达到最大,说明桩内部土体绕此处发生旋转,使得此处以上桩侧土抗力增加,而以下由于桩与土脱离,而造成桩侧土抗力减小.
由图8(b)可知,桩逆载侧内壁土抗力沿埋深分布规律与顺载侧内壁土抗力基本一致,仅在距桩底端2 m范围内有所不同.
2.6 不同循环次数下桩身位移
为了研究水平位移随时间的变化规律,对不同循环时泥面处和桩底端水平位移时程曲线进行了对比分析,第N次循环时泥面处桩身和桩底端水平位移变化曲线如图9所示.
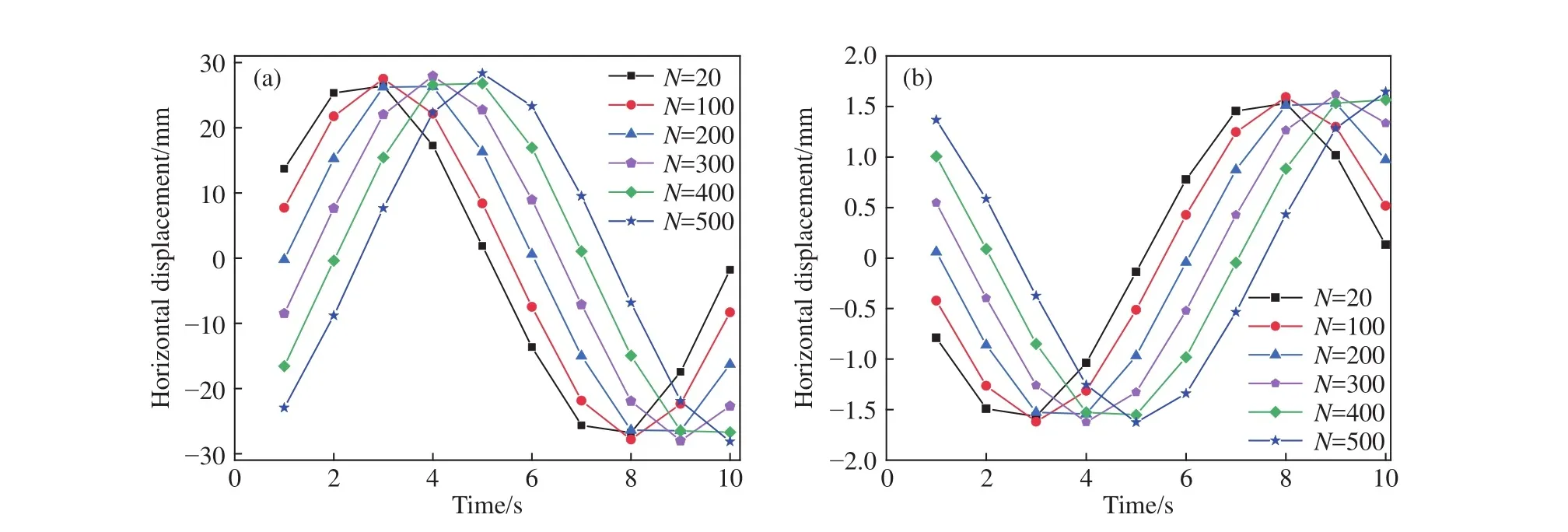
图9 第 N 次循环时泥面处桩身和桩底端水平位移. (a)泥面处;(b)桩底端Fig.9 Horizontal displacement of pile shaft at mud surface and pile bottom at the Nth cycle: (a) at the mud level; (b) bottom end of pile
由图9(a)可知,前3 s泥面处桩身位移随着循环次数的增加沿y轴逐渐下移,位移绝对值先减小后增加,3~5 s位移全部为正,而 5~8 s泥面处桩身位移随着循环次数的增加沿y轴逐渐上移,后2 s位移全部为负,由于结构和荷载的对称性,正向荷载作用时和负向荷载作用时桩身水平位移规律类似. 不同循环时泥面处桩身水平位移均呈现出周期性的变化.
从图9(a)还可以看出,第20次和第100次循环时位移最大正值和最小负值分别发生在3和8 s,在第200次和第300次循环时在4和9 s分别产生最大正值和最小负值,当循环次数为400和500次时,5 s位移最大,第 10 s位移最小,说明随着循环次数的增加,产生最大水平位移的时间点滞后. 不同循环次数下正向位移最大值分别为26.41、27.51、26.28、27.93、26.8和 28.32 mm,负向位移最大值分别为−26.79、−27.85、−26.46、−28.02、−26.72和−28.14 mm,同一时刻下发生的桩身最大位移值随循环次数的增加而增大,说明桩身最大位移不断累积. 由图9(b)可知,桩底端水平位移与泥面处桩身水平位移规律类似.
第N次循环结束时泥面处桩身和桩底端水平位移变化曲线如图10所示.

图10 第 N 次循环结束时泥面处桩身和桩底端水平位移. (a)泥面处;(b)桩底端Fig.10 Horizontal displacement of pile body at the mud surface and pile bottom at the end of the Nth cycle: (a) at the mud level; (b) bottom end of pile
由图10(a)可知,不同循环结束时泥面处桩身水平位移均为负,分别为−1.82、−8.32、−16.31、−22.71、−26.72和−28.14 mm,随着循环次数的增加,泥面处桩身水平位移绝对值逐渐增大,且增加的幅度越来越小,说明桩周土体强度随循环次数的增加而逐渐弱化,引起桩及桩周土体变形较大,且随着循环次数的增加变形逐渐趋于稳定.
由图10(b)可知,不同循环结束时桩底端位移均为正,分别为 0.13、0.52、0.97、1.33、1.57和1.65 mm,随着循环次数的增加,桩底端水平位移逐渐增大,且增加的幅度逐渐变小.
3 数值计算结果对比分析
由于模型试验中桩的直径相对较小,无法直接与本文数值模型中的大直径桩进行对比验证,故与已有的有限元分析结果进行对比分析. 文献[27]中陈新奎采用ABAQUS对大直径桩的水平受荷特性进行了模拟,并将数值模拟结果与风电场现场试桩结果进行了对比分析,验证了ABAQUS数值模拟的可靠性. 取文献[27]中4 MN(此荷载与本文荷载幅值最接近)水平力作用下桩身水平位移、剪力、弯矩与193 s时桩身水平位移、剪力、弯矩(此时桩身水平位移、剪力、弯矩最大)进行对比分析,如图11~13所示.
从图 11~13可以看出,图(a)与图(b)中泥面以下范围内桩身水平位移、剪力、弯矩沿埋深变化规律类似. 由图11可知,桩身水平位移曲线沿埋深均出现零点,均呈现出非线性的变化,桩均绕桩身轴线上某一点转动,表现出刚柔桩的性质. 由图12可知,泥面以下范围内桩身剪力均出现反弯点,图12(a)中桩身剪力变化幅度较大,究其原因,桩身水平位移较大,引起桩周土体压缩范围较大,能够提供较大的土抗力[28−29],导致剪力变化程度较大. 由图13可知,泥面以下范围内桩身弯矩沿埋深均没有出现反弯点,均沿埋深先变大后变小,最大值均发生在浅层土体,桩底端弯矩均接近于零.
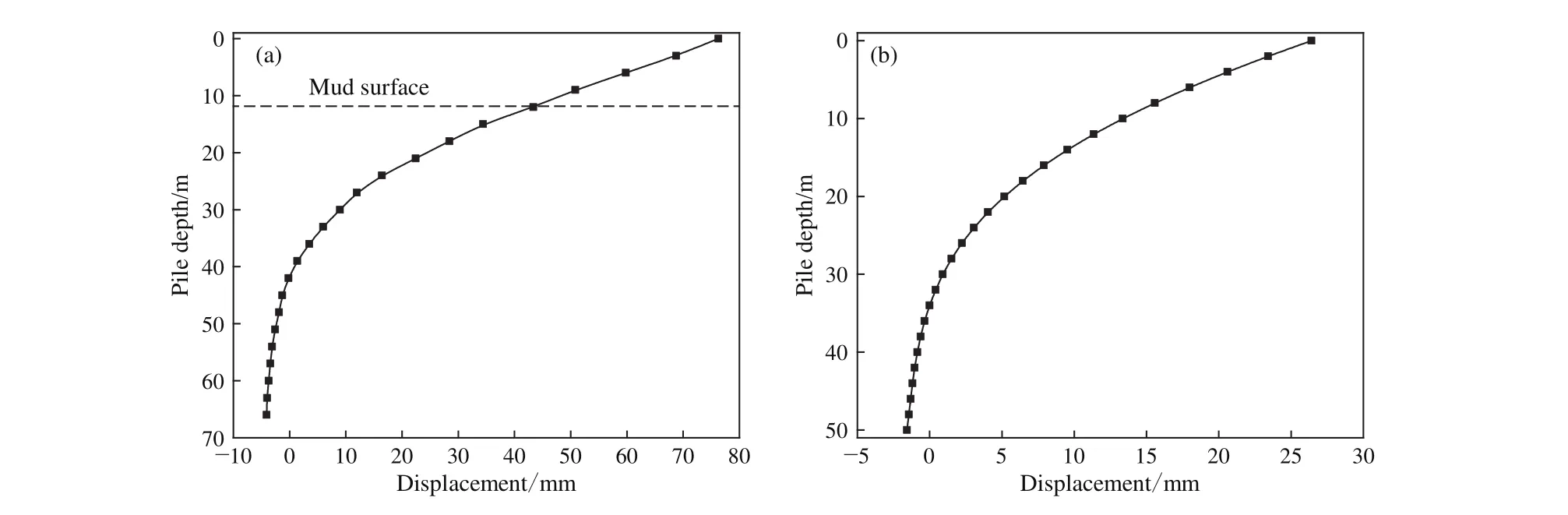
图11 桩身水平位移对比分析. (a)4 MN 水平力作用下桩身位移[27];(b)193 s 时桩身位移Fig.11 Comparative analysis of horizontal displacement along the pile shaft: (a) pile displacement under 4-MN horizontal force[27]; (b) pile displacement at 193 s
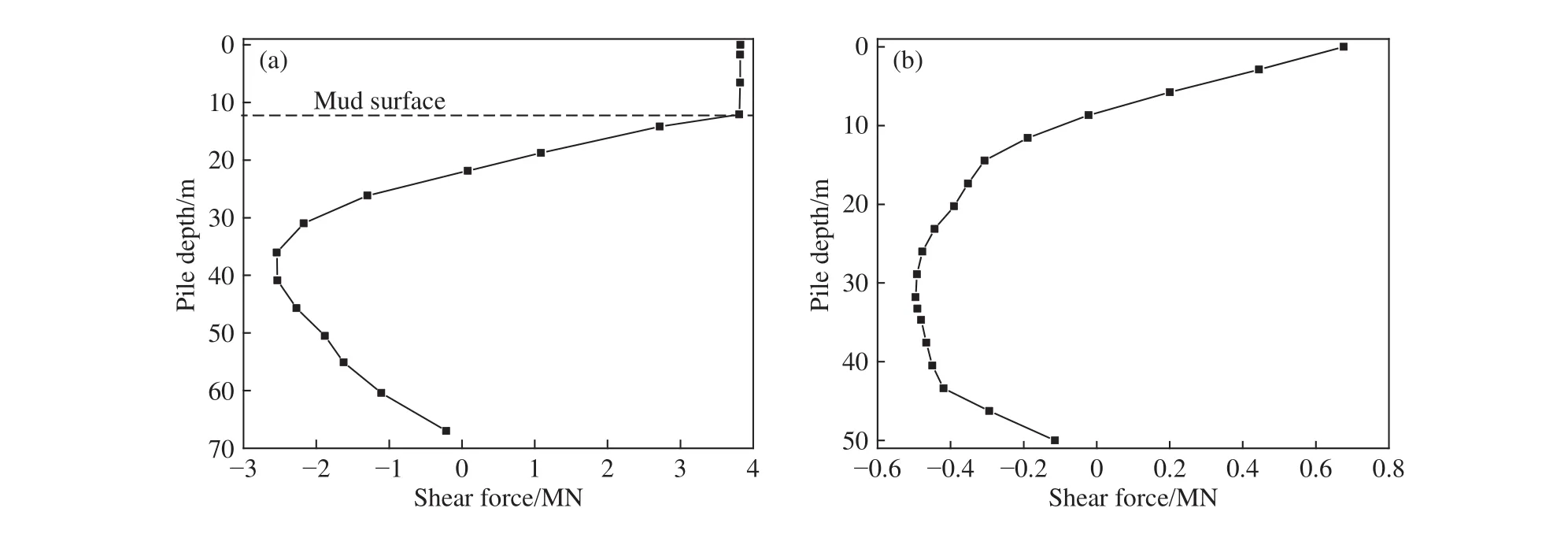
图12 桩身剪力对比分析. (a)4 MN 水平力作用下桩身剪力[27];(b)193 s时桩身剪力图Fig.12 Comparative analysis of shear force along the pile shaft: (a) pile displacement under 4-MN horizontal force[27]; (b) pile displacement at 193 s

图13 桩身弯矩对比分析. (a)4 MN 水平力作用下桩身弯矩[27];(b)193 s 时桩身弯矩图Fig.13 Comparative analysis of bending moment along the pile shaft: (a) pile displacement under 4-MN horizontal force[27]; (b) pile displacement at 193 s
综上可知,本文运用ABAQUS建立的数值模型是可靠的,且数值模拟结果是准确的.
4 结论
(1)桩绕桩身轴线上某一点转动,表现出刚柔桩的性质;不同循环时泥面处桩身水平位移均呈现出周期性的变化;随着循环次数的增加,泥面处桩身最大位移发生的时间点滞后,桩身水平位移绝对值逐渐增大,且增加的幅度越来越小,逐步趋于稳定,桩身水平位移随时间变化逐渐累积.
(2)由于桩周土体的抵抗作用出现反向剪力值,不同时间点的桩身剪力反弯点位于埋深7~9 m范围内,随桩身剪力绝对值的增大而沿埋深有所下降;不同时间点剪力沿x轴正方向最大值均位于泥面处,沿x轴负方向最大值均位于埋深31~32 m 范围内.
(3)不同时间点桩身弯矩均没有出现反弯点,弯矩最大值均位于泥面下7~9 m范围内,与桩身剪力零点位置相对应,发生在浅层土体;不同时间点桩底端的弯矩接近于零,说明桩底部土体对桩的嵌固作用明显.
(4)淤泥土和粉砂土分界面处由于土层之间性质差异较大,导致桩外壁土抗力增加显著;桩身外壁土抗力沿埋深曲线随时间的变化出现分界点,分界点上下范围内土抗力随时间变化规律正好相反;桩身外壁土抗力的发挥不仅仅取决于桩土相对位移,还与埋深和桩侧土层性质有关;不同时间点桩身内壁土抗力曲线沿埋深几乎重合,承担的荷载基本不变.
