伪刚体-柔体耦合的新式免充气轮胎刚度分析
2021-05-19张陈曦赵又群冯世林
张陈曦 赵又群 冯世林 郑 鑫 徐 瀚
南京航空航天大学能源与动力学院,南京,210016
0 引言
轮胎的径向刚度特性是轮胎性能的一项重要评价指标,反映了轮胎所能承受负荷的能力。轮胎径向刚度会影响其受载荷后的变形情况,还会影响其行驶阻力与乘坐舒适性。因有别于普通充气轮胎气压支撑的特点,且市场上不同厂商的免充气轮胎在结构上也不同,故需对特定的免充气轮胎刚度特性进行研究。王强等[1]利用曲梁理论建立弹性封闭圆环曲梁模型,对免充气轮胎刚度进行了分析。FORD等[2]利用声学方法测量了轮辋的径向弯曲刚度和横向扭转刚度。VU等[3]利用任意Lagrangian Eulerian法建立环状可变形固体的计算公式,并将该公式应用在新的简化轮胎振动模型中。ROMANO等[4]提出了非充气轮胎的环形模型,由曲线的Timoshenko梁和Hamilton变分原理导出了轮胎的运动方程。
目前,市面上的免充气轮胎多使用合成橡胶材料作为其力学结构支撑,弹塑性较好,利于车辆的平顺行驶[5],但径向刚度普遍不高。在面临重载、高冲击的工作环境(如重型卡车的工作和高空抛掷运输工具)时,多数情况下充气、免充气轮胎变形严重甚至损毁。针对重载、高冲击问题,本课题组发明了一种利用伪刚体和輮轮组合结构的伪刚性免充气轮胎[6]。所谓的伪刚体,是一种柔顺结构,可利用其柔性变形获得所需的运动,特点是用较少零件可完成复杂运动,减小质量、经济成本,在仿生、机器人领域用途广泛,近年来对伪刚体的研究方兴未艾。VENKITESWARAN等[7]利用伪刚体模型研究了等截面圆形梁在受外力和弯矩共同作用下的运动学和刚度特性,便于机构方程的推导和快速求解。KE等[8]采用有限元分析法研究了不同曲度的屈曲足假体(伪刚体)在站立和跑步时的应力和位移变化情况。BILANCIA等[9]描述了一种计算机辅助设计/工程(CAD/CAE)框架,用于自动获得精确的伪刚体模型参数,得到其位移和柔度以及复杂挠曲的形状优化方法。
为研究伪刚性免充气轮胎的径向刚度特性,本文采用伪刚体模型和柔体弹性力学模型耦合求解的方法,分析其在不同受载情况下的轮胎下沉量及变形情况。
1 伪刚性免充气轮胎简介
伪刚性免充气轮胎的典型结构如图1所示,包含轮毂、板簧和輮轮等结构,其輮轮结构采用了橡胶包裹金属骨架的制造工艺。轮毂四周铰接有若干个均布的板簧结构,板簧末端又与輮轮的骨架铰接。此种轮胎在使用过程中,利用板簧和輮轮的缓冲机理,起到代替充气轮胎之利用橡胶和气压承重、缓冲的作用。
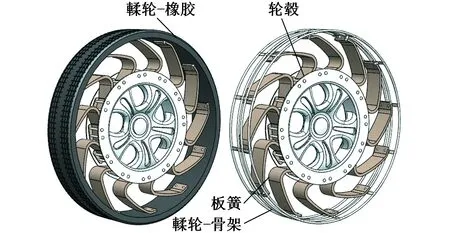
图1 伪刚性免充气轮胎结构示意图Fig.1 Structural diagram of pseudo-rigidnon-pneumatic tire
为研究伪刚性免充气轮胎的径向刚度特性,对其进行伪刚体-柔体耦合的力学模型的构建,提供一种分析板簧、輮轮结构的便利数学模型。根据伪刚性免充气轮胎受径向力时的结构特征,可将其沿轴向简化为平面问题,在轮毂几何中心处建立直角坐标系Oxy,第i个板簧连接轮毂的那一端记为Oi点,建立板簧件直角坐标系Oixiyi。记第i个板簧在以O点为中心、x正轴逆时针旋转θi的位置。伪刚性免充气轮胎平面结构简图及各坐标轴位置、正向如图2所示。

图2 伪刚性免充气轮胎平面图Fig.2 Structural plan of pseudo-rigidnon-pneumatic tire
2 伪刚性免充气轮胎力学建模
伪刚性免充气轮胎的径向刚度受板簧和輮轮骨架的影响较大,此时可忽略輮轮橡胶层对刚度的影响,轮毂则看作刚体。为此,分别对板簧和輮轮骨架建立力学模型,并进行耦合求解。
2.1 板簧力学建模
板簧结构是一种有复杂几何形状的柔性部件,其受力过程中呈现非线性位移变形。伪刚体模型可以提供一种分析非线性变形系统的简单方法,通过将连续的柔性结构分割成一定数量的由扭簧铰接的刚性段,并利用多刚体理论计算从而模拟出此柔性体的变形过程。本研究采用伪刚体模型对板簧结构进行力学分析。
2.1.1板簧伪刚性段的划分
对板簧进行伪刚性段划分,采用曲率分段原则和刚度分段原则[10]相结合的划分方式。设单个板簧的总弧长为S,初始假定划分段数为N,第i(i=1, 2,…,N)划分段的弧长为si。划分开始时,首先应判断被划分线段的曲直情况,当线段分别为直线、曲线或曲直线过渡段时,按曲率分段原则分别计算si:
直线:si=S/N
(1)

(2)
(3)

因节省材料、减小质量,板簧厚度e从连接轮毂处向外逐渐变薄,故还需按刚度分段的原则对上文得到的si进行修正,修正公式为
si=λisi
(4)
式中,λi为第i划分段的刚度系数(表示此段平均刚度与整条板簧平均刚度的比值)。
为防止因曲率过大,使得分段弧长si的长度过长或过短,约定si最大不超过smax,最小不低于smin。根据上述划分方法,依次沿板簧曲线进行分割,最终统计划分段数n、长度si。板簧曲线划分的流程示意图见图3。
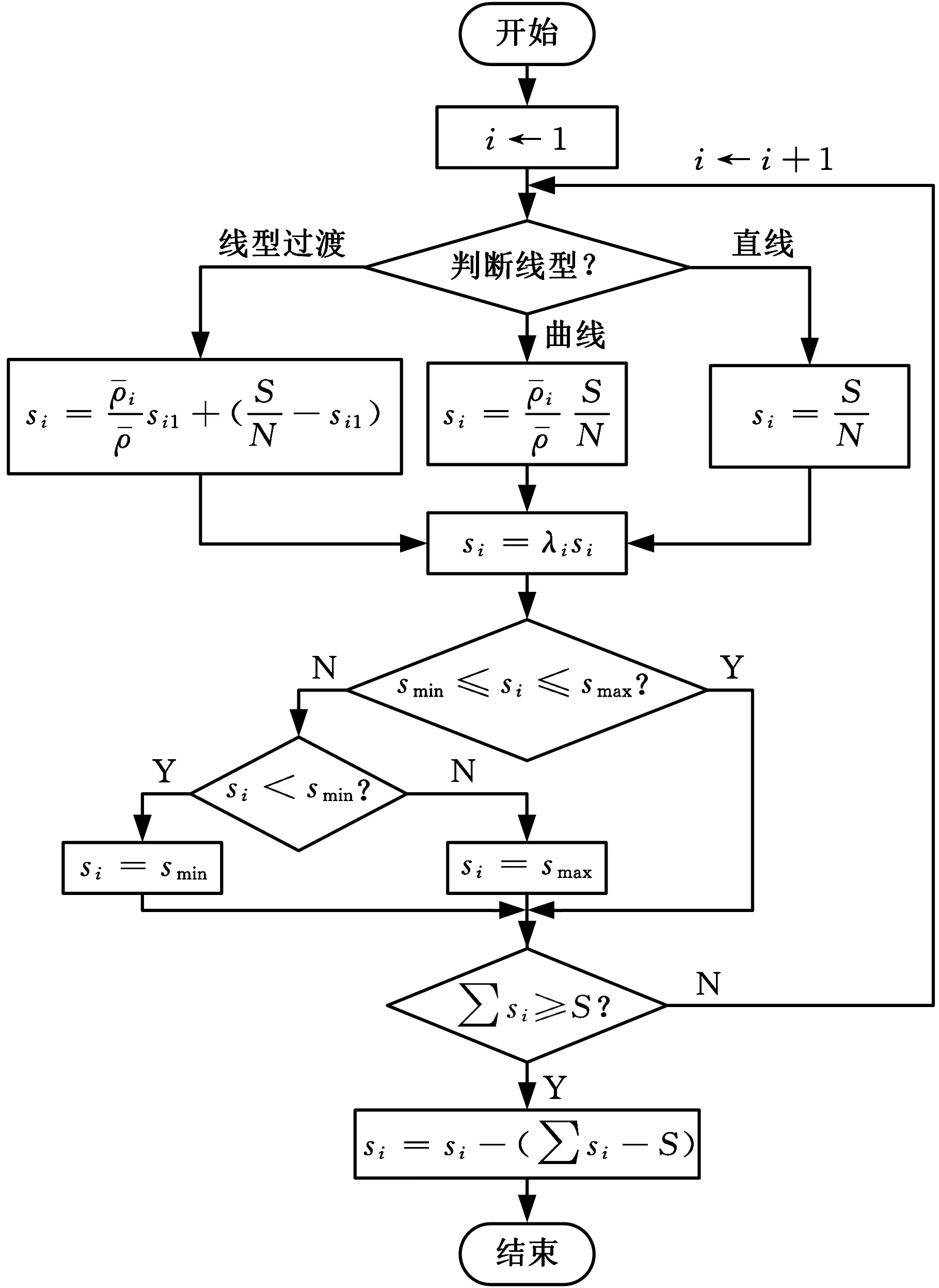
图3 板簧曲线划分流程图Fig.3 Flow chart of division about plate spring curve
伪刚体模型中,柔性板簧结构被分割成一定数量的由扭簧铰接的刚性段(图4所示的柔性铰链连接方式)。铰接的扭簧常数[11]为
K=γKΘEI/l
(5)
式中,γ为特征半径系数;KΘ为刚度系数(关于γ和KΘ的计算见文献[11],不再赘述);E为板簧弹性模量;I为截面惯性矩;l为刚性段长度。
考虑到板簧伪刚性结构存在曲线和变截面的几何特性,故划分后的各伪刚性段之间的扭簧常数可在添加修正系数η后进行计算。修正后的第i扭簧常数方程为
Ki=ηγiKΘiEIi/li
(6)
2.1.2板簧的变形位移求解
利用前文已划分好的伪刚性段结构,分析其受力变形情况。如图4所示,令
wp=[fxpfypτp]Tτ=[τ1τ2…τn]T
其中,wp表示伪刚体终端所受的外力和外力矩,fxp、fyp为外力在坐标系Oixiyi下的分量,τp为外力矩;τ表示各杆与前一杆间关节处的扭矩,有τi=-Ki(ψi-ψsi),ψsi为变形前第i杆与第i-1杆杆间逆时针方向的夹角,ψi为变形后第i杆与第i-1杆间逆时针方向的夹角。考虑到第i伪刚性段重力远小于外力wp,故可忽略此i段所受重力。
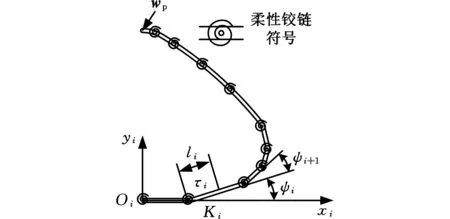
图4 伪刚性段结构参数Fig.4 Structure parameters of pseudo-rigid segment
则板簧在Oixiyi平面力系中有如下力矩平衡[12]关系:
(7)
其中,Gp为外力的一阶影响系数矩阵,令s1~n表示sin(ψ1+ψ2+…+ψn),c1~n表示cos(ψ1+ψ2+…+ψn),则Gp可写成
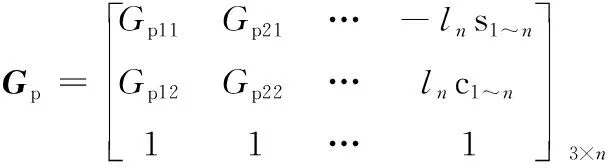
当扭簧扭矩或外载荷有微小变化时,对式(7)取变分,有
(8)
因为
其中,Hp为外力的二阶影响系数矩阵;⊗表示矩阵的Kronecker积。故式(8)可写成
所以
D=[DxDyDr]T
式中,Dx为坐标系Oixiyi下板簧末端的x向位移;Dy为y向位移;Dr为位移角。
当分析板簧一次受力过程且其变形位移D较小时,有
(9)
由此得到板簧受力变形的位移计算公式。
2.2 輮轮骨架力学建模
图1中的輮轮骨架为一种圆环结构,适合采用弹性力学的极坐标解法分析其位移变形。
2.2.1骨架的极坐标力学表述
輮轮骨架在受径向力作用时,其变形可看作与轴向位置无关,故骨架受力变形分析按二维极坐标下的平面应变问题考虑。按图5a建立极坐标系Ox,将骨架结构沿轴向投影于一平面,取骨架圆周平面的几何中心为极点O,以O点水平向右的方向为极轴x正向,平面上各点与极轴间的极角为θ;骨架内圈与12个均匀分布的板簧相连接,12个连接点在内圈θj= (j-1)π/6(j=1,2,…,12)处;如图5b所示,骨架内圈半径为a,外圈半径为b,规定骨架内外圈受正应力、切应力的正方向如图5b中箭头方向。

(a)建立极坐标系 (b)骨架内外圈受 正应力、切应力图5 輮轮骨架几何参数示意图Fig.5 Schematic diagram of geometric parametersabout the skeleton of the elastic wheel disk
采用半逆解法求解輮轮骨架的应力及变形。设輮轮骨架在极坐标系下的Airy应力函数U具有分离变量形式的解[13],形如U(r,θ)=R(r)T(θ),将它代入双调和方程后,有以下通解形式:

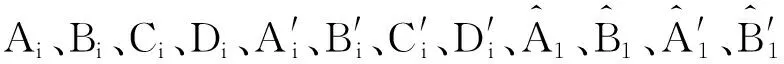

(10)
已知上述骨架圆环的Airy应力函数U在极坐标系下有径向正应力σr、环向正应力σθ和切应力τrθ,其表达式如下:
(11)
由式(11)和极坐标下平面应变问题的本构关系,可得骨架圆环的径向位移ur和切向位移uθ:
(12)
f(θ)=L1cosθ+L2sinθg(θ)=L3r
式中,E′为骨架材料弹性模量;ν为材料泊松比;f(θ)、g(r)为因积分产生的常量函数;L1、L2、L3均为常数。
2.2.2骨架的边界条件与求解
上文提到轮毂四周均匀安装有12根板簧。当各板簧受车轮径向力变形后,车轮几何中心由O点移动到O′点处,如图6所示。此时假设各板簧对輮轮骨架的作用力为Fj,Fi与极轴Ox的夹角为φj(轮胎垂直地面下沉时,应有骨架内圈受力点4和10的极角位置不变,故有φ4=θ4=π/2,φ10=θ10=3π/2),地面对骨架的支持力为FN。考虑到图2所示的板簧在小变形情况下对輮轮骨架的作用力关于y轴对称,所以对骨架受力分析时仅考虑Fj(j=1,2,3,4,10,11,12)和FN对骨架变形的影响。则关于Fj(j=1,2,3,4,10,11,12)和FN的力平衡关系如下:
(13)

图6 輮轮骨架假设的受力方向Fig.6 The assumed force direction for the skeleton ofthe elastic wheel disk
若设各个力Fj和FN的作用区域在圆环骨架2α弧度的弧长上,圆环厚为h,则骨架的圆环外圈有应力边界条件如下:
(14)
骨架的圆环内圈有应力边界条件:
(15)
按式(15)将圆环骨架的应力边界展开成三角级数形式,有
(16)
同理可得a′0、a′n、b′n和c′0、c′n、d′n。比较代入式(10)后的式(11)和式(16),可提取相同位置项的系数组成等式,构成方程组用于后续求解。
考虑到车轮受径向力作用轮胎下沉时,图5极坐标系Ox的车轮外圈在3π/2处应无切向位移,且无切向斜率;在θj(j=1,2,…,12)处的位移应与图2坐标系Oixiyi下板簧末端位移一致,在变换直角坐标系Oixiyi和极坐标系Ox位置和方向后,由式(9)、式(12)可得骨架圆环内外圈的位移边界条件:
(17)
2.3 伪刚体-柔体耦合模型的建立

3 伪刚性免充气轮胎径向刚度分析
利用上文建立的伪刚体-柔体耦合模型对伪刚性免充气轮胎的径向刚度进行仿真分析。
3.1 板簧划分结果
令坐标系Oixiyi下的板簧曲线方程如式(18),单位mm。板簧宽100 mm,始端板厚为15 mm,终端板厚为10 mm,板厚沿板簧弧长线性下降,弹性模量为210 GPa。设定的初始划分段数N为30,按图3所示的划分流程,得到最终完成划分的各段弧长及坐标,划分结果如图7所示,最终划分段数n为28。有
yi=
(18)
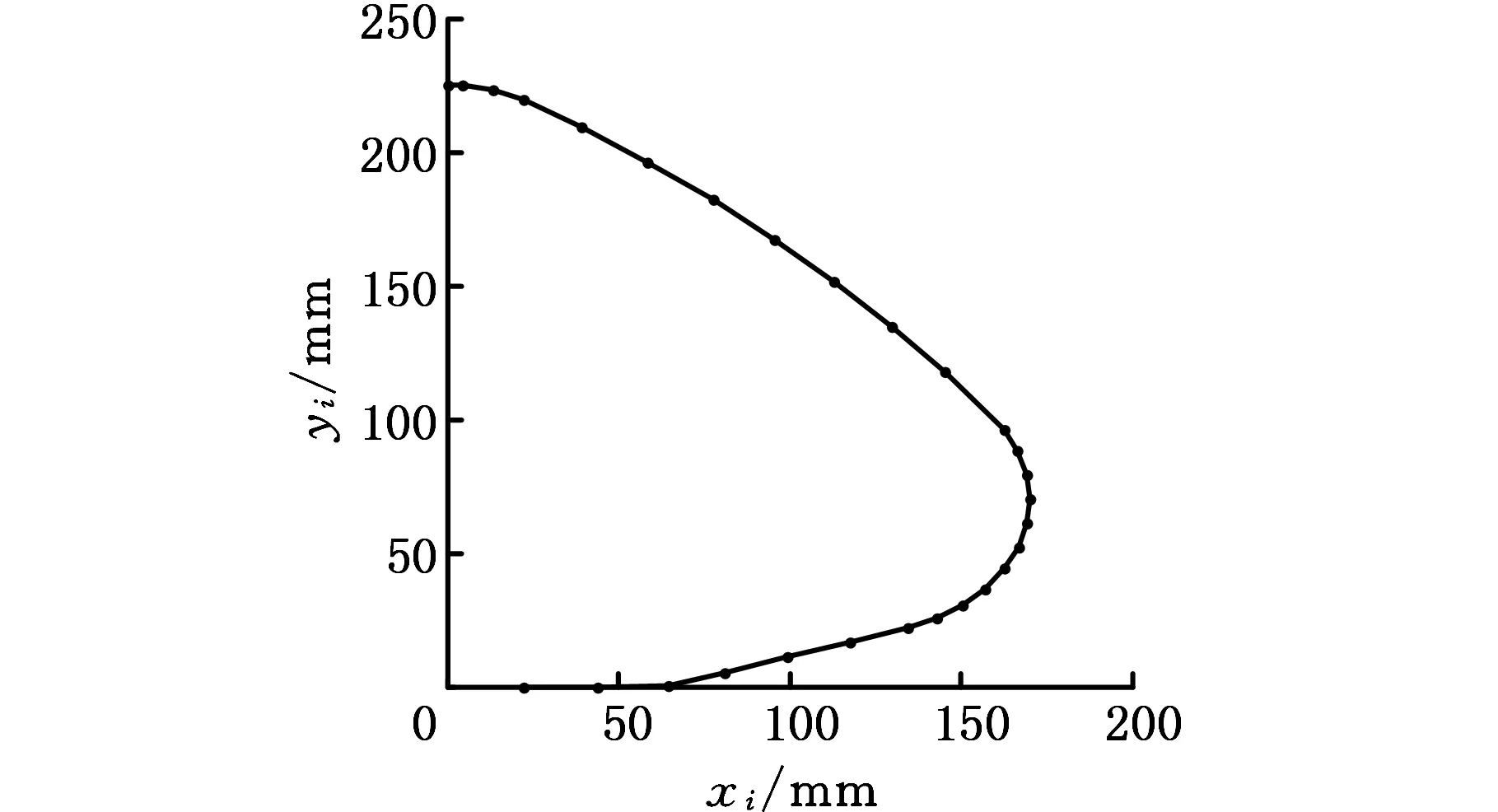
图7 板簧曲线划分结果Fig.7 The result of plate spring curve division
3.2 车轮径向刚度的求解
伪刚性免充气轮胎工作时,其径向刚度受到各板簧作用力的影响。考虑到板簧对胎面的支撑作用不像普通充气轮胎的胎面受气压力均衡分布,选取两个典型工位进行径向刚度分析,如图8所示。在工位一,垂直径向位置有一板簧直接支撑受力的轮胎;在工位二,轮胎垂直径向位置没有板簧直接支撑,不妨令此位置在两板簧安装位置的正中间。
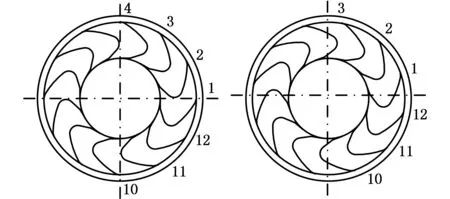
(a)工位一 (b)工位二图8 两种工位Fig.8 Two working positions
3.2.1工位一
设輮轮骨架的内半径a为475 mm,外半径b为495 mm,骨架由4根圆环组成,单个圆环截面厚h为10 mm,材料弹性模量E′与板簧相同,泊松比ν为0.3,轮胎受垂直径向力的作用。结合前述伪刚体-柔体耦合建模过程,利用MATLAB求解不同载荷条件下輮轮骨架位移变形及轮胎下沉量(在不影响精度的情况下,式(10)和式(16)的级数部分取前4项即可)。
为验证伪刚体-柔体耦合模型的正误,利用有限元软件ABAQUS建立了伪刚性免充气轮胎板簧与骨架的三维有限元模型(图9),对车轮径向刚度进行静力学有限元分析。作为对比的有限元模型在保留原有约束关系的前提下,对原零部件的结构进行简化。与伪刚体-柔体耦合模型一样也忽略了橡胶层结构,将轮毂和地面作刚体约束,地面完全固定,并设置骨架与地面的接触;板簧首尾两端分别与轮毂、輮轮骨架建立绑定约束,从而固定板簧首尾端的位置;创建车轮几何中心点,将此点与轮毂耦合后用于限制轮毂仅能在y向移动,后续施加的质量力也通过此点传递给轮毂;板簧与骨架采用非协调单元C3D8I单元,此种单元可克服剪切自锁,适合分析弯曲问题;模型共划分单元总数为7032。

图9 轮胎有限元模型Fig.9 Finite element model of tire
上述两种方法运算后,结果如下:
(1)在工位一,轮胎受10 kN、30 kN、60 kN垂直径向力条件下,两种方法计算的轮胎下沉量及相对有限元方法计算解的误差比较见表1。图10是轮胎下沉量受载荷影响的关系图,实线是MATLAB计算的伪刚体-柔体耦合模型结果,虚线是Abaqus计算的有限元模型结果,从中可以看出,此种轮胎的载荷与下沉量近似成正比,其径向刚度比一般普通轮胎大,适合在重载、高冲击环境下使用。
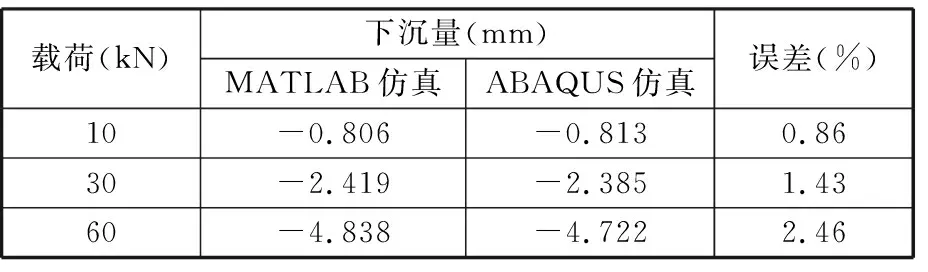
表1 工位一不同受力下的轮胎下沉量

图10 工位一载荷-下沉量关系Fig.10 Relation between load and sinkage displacementin first working position
(2)利用伪刚体-柔体耦合模型计算的下沉量结果与有限元计算的结果相似,受力较小时,两者结果接近度较好,误差较低;受力较大时,伪刚体-柔体耦合模型计算的下沉量会逐渐略大于有限元计算的结果,考虑到式(8)在小变形条件下成立的特点,且仅取式(10)和式(16)的级数项前4项,随着板簧和骨架变形增大,其计算结果会有少许偏差,但偏差的数量级在宏观尺度上可忽略。
(3)此次运算采用的计算机配置如下:CPU为Core i5-3470,RAM为8GB。建模完成后的计算过程中,ABAQUS分析有限元模型在几种工况下的平均运算时间为118.08 s,MATLAB分析伪刚体-柔体耦合模型的平均运算时间为9.37 s;从时间上比较,伪刚体-柔体耦合模型在得到近似结果的情况下,运算时间大幅缩短,减少了工作周期。
(4)图11~图13分别是工位一时受10 kN、30 kN、60 kN垂直径向力后輮轮骨架内圈的形变图,图11的变形量放大了50倍,其他变形量放大了10倍,从中可以看出:两种计算方法得到的骨架内圈变形结果近似;受力较小时,两者结果吻合度较好,受力较大时,伪刚体-柔体耦合模型计算的骨架变形量略大于有限元计算的结果。

图11 工位一10 kN骨架内圈形变(放大50倍结果)Fig.11 Deformation of skeleton inner ring under10 kN load in first working position(result is magnified by 50 times)

图12 工位一30 kN骨架内圈形变(放大10倍结果)Fig.12 Deformation of skeleton inner ring under30 kN load in first working position(result is magnified by 10 times)

图13 工位一60 kN骨架内圈形变(放大10倍结果)Fig.13 Deformation of skeleton inner ring under60 kN load in first working position(result is magnified by 10 times)
(5)参照图2坐标系Oxy方向和图8中工位一板簧位置,当轮胎受10 kN质量力时,伪刚体-柔体耦合模型求解得到的板簧受力Fj(j=1,2,3,4,10,11,12)在x、y向的分量及其受力支撑的贡献度见表2,可见板簧10对轮胎y向垂直支撑起到主要贡献作用,板簧11、12对阻碍轮胎x向变形起到主要贡献作用。作为对比,分别提取ABAQUS中轮胎在y向、x向的位移变化结果,如图14、图15所示,可知各板簧变形情况与伪刚体-柔体耦合模型计算的受力大小吻合。

表2 工位一10 kN下各板簧受力及贡献度

图14 工位一10 kN下轮胎y向位移Fig.14 The y direction displacement of the tireunder 10 kN load in first working position

图15 工位一10 kN 下x向位移Fig.15 The x direction displacement of tireunder 10 kN load in first working position
3.2.2工位二
工位二的求解方式与工位一设置的载荷及边界条件相同,仍比较伪刚体-柔体耦合模型与有限元模型的分析情况。结果如下:
(1)从表3、图16中看出,伪刚体-柔体耦合模型与有限元模型的计算结果和工位一的结论一致。
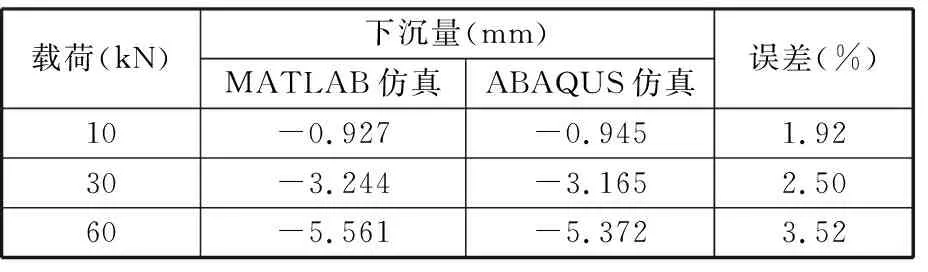
表3 工位二不同受力下的轮胎下沉量

图16 工位二载荷-下沉量关系Fig.16 Relation between load and sinkage displacementin second working position
(2)前文假设轮内均布的板簧在小变形时左右受力相同,但在图17~图19工位二的骨架内圈形变图中可以看出,ABAQUS的计算结果显示骨架内圈左右变形量稍有不一,但因数量级较小,不影响对整体变形趋势的把握,故可忽略。
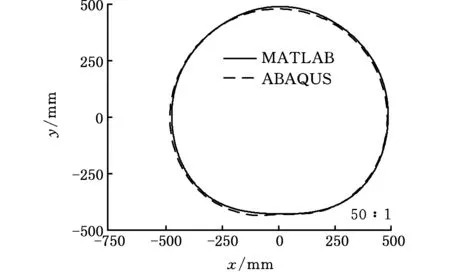
图17 工位二10 kN骨架内圈形变(放大50倍结果)Fig.17 Deformation of skeleton inner ring under10 kN load in second working position(result is magnified by 50 times)

图18 工位二30 kN骨架内圈形变(放大10倍结果)Fig.18 Deformation of skeleton inner ring under30 kN load in second working position(result is magnified by 10 times)

图19 工位二60 kN骨架内圈形变(放大10倍结果)Fig.19 Deformation of skeleton inner ring under60 kN load in second working position(result is magnified by 10 times)
(3)以图8中工位二板簧位置,轮胎受10 kN质量力时的板簧受力Fj(j=1,2,3,10,11,12)在x、y向的分量及其受力支撑的贡献度见表4,可见仍然是板簧10对轮胎y向垂直支撑起主要贡献作用。板簧11、12对阻碍轮胎x向变形起主要贡献作用;作为对比提取的ABAQUS轮胎y向位移变化(图20)、x向位移变化(图21)与伪刚体-柔体耦合模型计算的受力大小吻合。
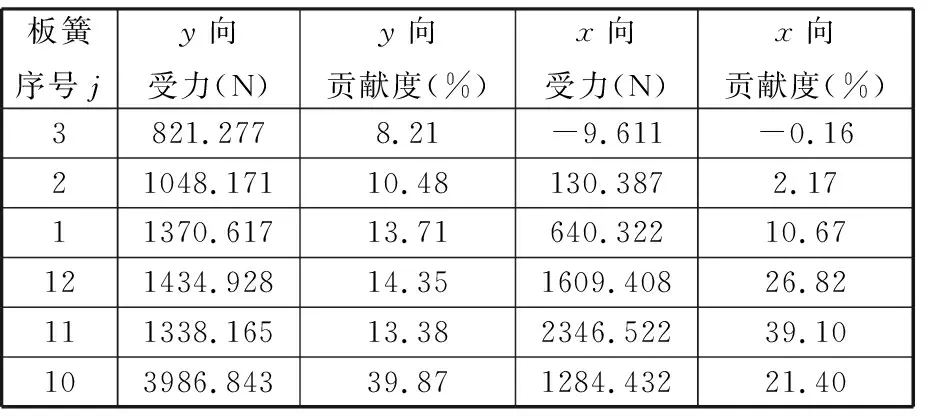
表4 工位二10 kN各板簧受力及贡献度
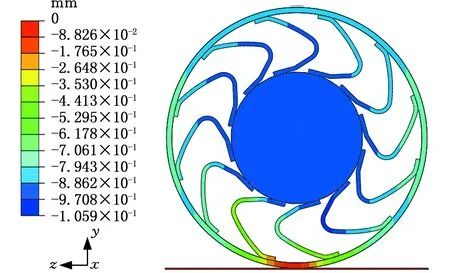
图20 工位二10 kN轮胎y向位移Fig.20 The y direction displacement of the tireunder 10 kN load in second working position
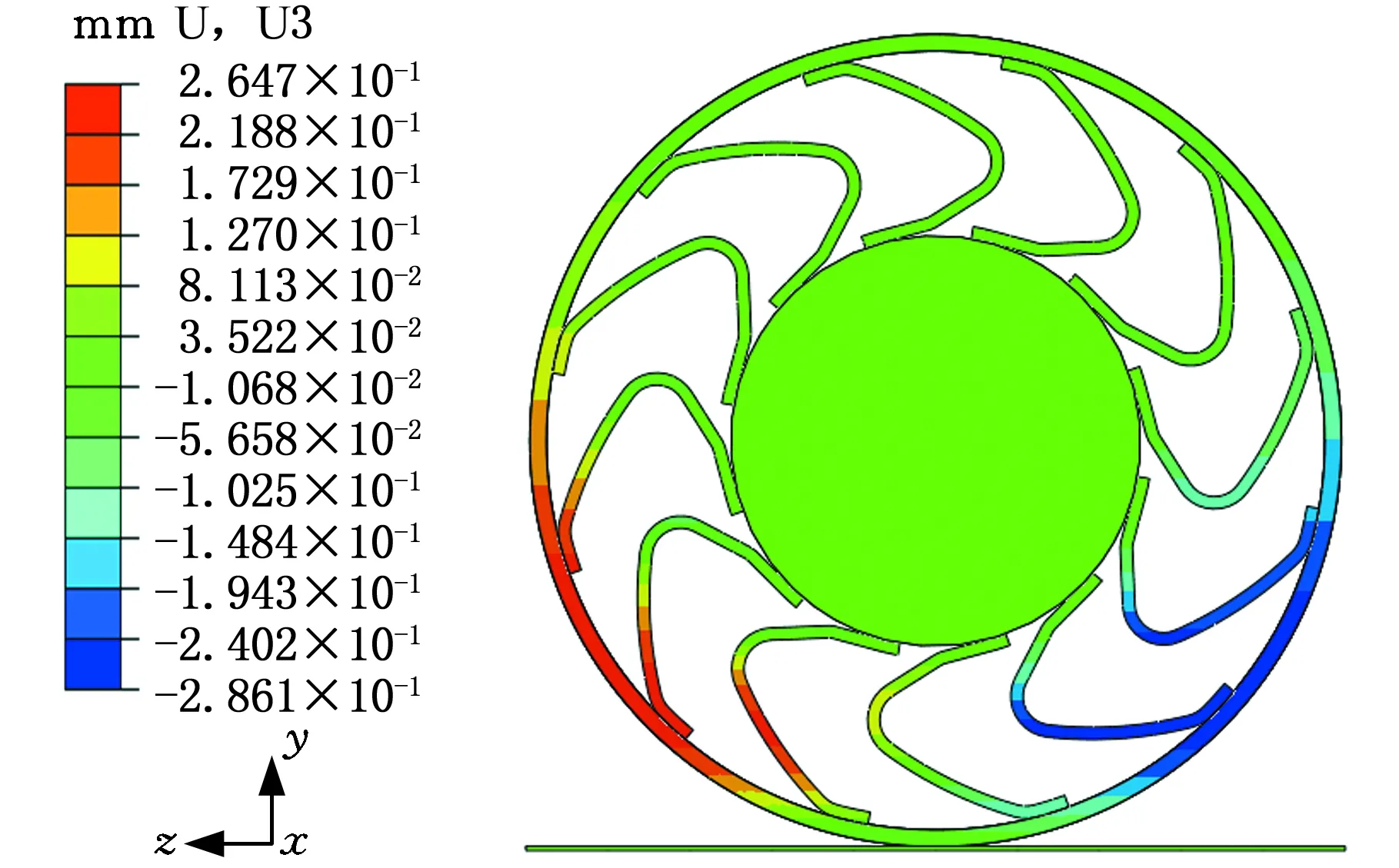
图21 工位二10 kN轮胎x向位移Fig.21 The x direction displacement of the tireunder 10 kN load in the second working position
(4)比较表3和表1,从下沉量结果上看,当失去板簧直接支撑作用后,工位二的下沉量比工位一的下沉量稍大,当轮胎滚动时,这种变刚度过程会对其平顺性产生影响。若相同质量力作用下轮胎径向刚度在工位一处为kⅠ、工位二处为kⅡ,工位一与工位二间径向刚度呈线性变化,又因轮胎均布有12个板簧,则在t时刻轮胎角速度为ω时,轮胎径向刚度k(t)满足:
则轮胎径向垂直运动的微分方程可表示为
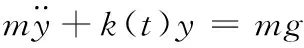
其中,m为轮胎和轮胎负载的质量,可根据上文所给初值求得轮胎滚动时的径向加速度变化及加速度功率谱密度,再由ISO2631-1:1997(E)标准规定的频率加权函数得到径向加权加速度均方根值aw,用于评估轮胎平顺性。10 kN质量力车速分别为40 km/h和70 km/h两种情况下的轮胎径向加权加速度均方根值见表5,由加权加速度均方根值和人的主观感觉间关系可知:当此轮胎在低速40 km/h工作时,人主观感觉良好,没有感觉不舒适;在高速70 km/h工作时,人会有稍许不舒适感觉,这说明高速情况下伪刚性免充气轮胎的平顺性还有提升空间。

表5 轮胎在两种车速下的加权加速度均方根值
3.3 车轮刚度优化
由上文知,伪刚性免充气轮胎径向刚度较大,若想按需降低其刚度,则可利用伪刚体-柔体耦合模型快速求解的特点对此轮胎的结构尺寸进行优化。考虑輮轮骨架及板簧尺寸对车轮刚度的影响,选取骨架外圈半径b和板簧厚度e为设计变量,工位一时的轮胎下沉量ξ(b,e)为优化目标,暂定约束条件为10 kN的轮胎下沉量不超过13 mm,则有
min -ξ(b,e)
s.t.ξ(b,e)-13≤0
调用MATLAB数据库中的遗传算法进行优化,优化结果见表6。

表6 优化前后的尺寸
优化后,骨架外半径b和板簧厚度e均变小,板簧厚由原来沿曲线的渐变厚度变为等厚。利用优化后的结构尺寸重新仿真轮胎下沉量及变形。伪刚体-柔体耦合模型的MATLAB仿真下沉量为-12.1902 mm,ABAQUS仿真的下沉量为-11.3346 mm,优化前后骨架的形变如图22所示。结果表明:通过减小骨架和板簧的厚度,可以起到减小伪刚性免充气轮胎径向刚度的作用;车轮下沉量较优化前有所增大,车轮径向刚度优化效果明显,可针对不同刚度需求,合理设计车轮尺寸。
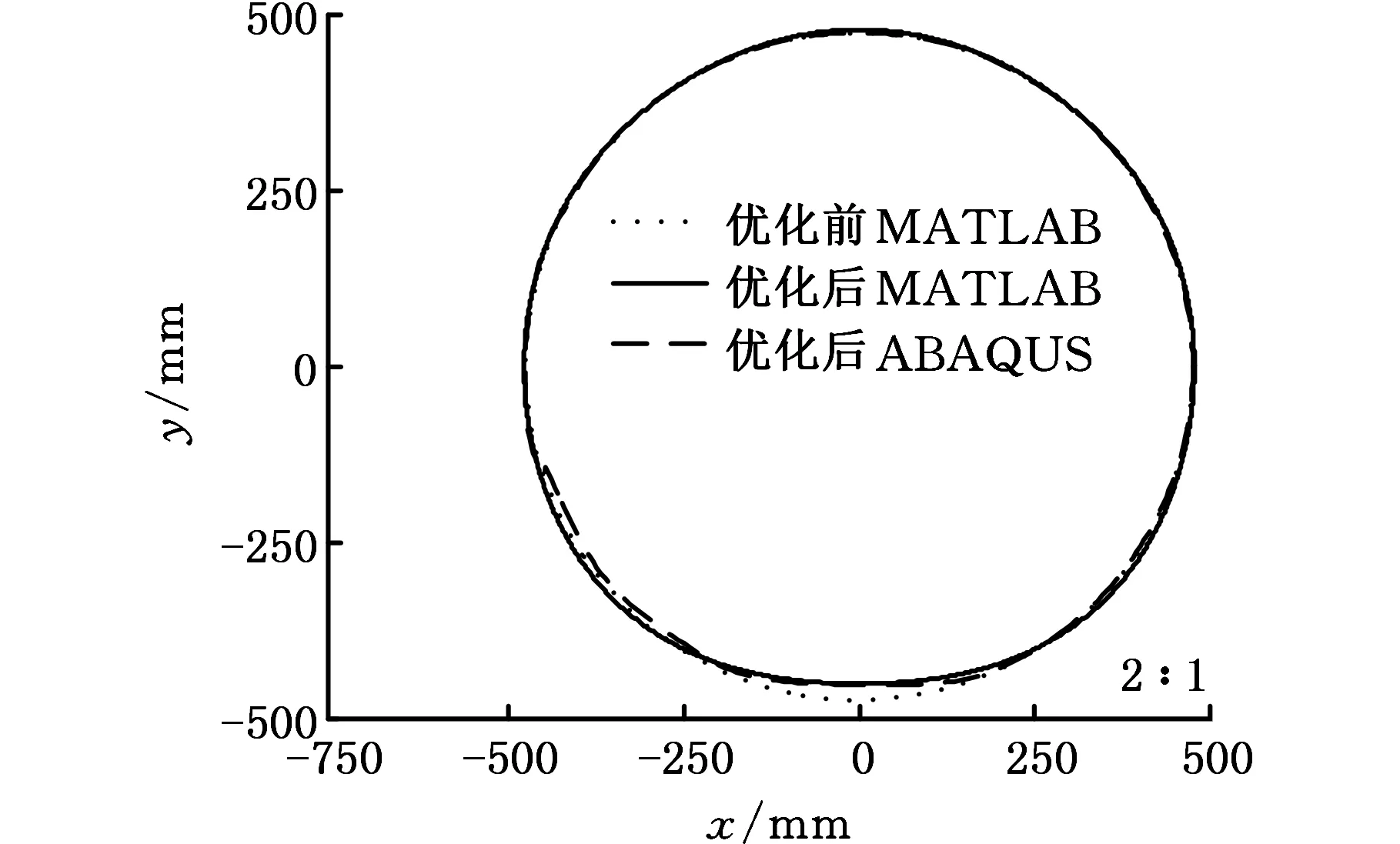
图22 优化前后骨架内圈形变比较(放大2倍结果)Fig.22 Comparison of inner ring deformation beforeand after optimization(result is magnified by 2 times)
4 结论
(1)本文采用伪刚体-柔体耦合模型对伪刚性免充气轮胎进行径向刚度分析,其下沉量与载荷间近似成正比,且伪刚性免充气轮胎径向刚度比一般普通充气/非充气轮胎大,适合在重载、高冲击的工作环境下使用。
(2)两种工位下,伪刚性免充气轮胎垂向下方的板簧均对支撑车轮起到主要贡献作用;不同工位间的轮胎下沉量有极小差距,低车速工作时能够满足平顺性要求,高车速工作时平顺性稍有欠缺。
(3)比较二维建模的伪刚体-柔体耦合模型与三维建模的有限元ABAQUS软件,两者在轮胎下沉量和变形的计算结果近似,吻合度高,但从建模完成的运算时间成本上看,伪刚体-柔体耦合模型计算时间明显较短。
(4)为适应不同刚度需求,利用已有的优化算法(如遗传算法)结合伪刚体-柔体耦合模型可以得到优化后的设计参数,合理降低伪刚性免充气轮胎的径向刚度,减少优化步骤,避免其他优化软件冗长的设置、二次开发过程。
