基于改进蚁群算法的汽车混流装配调度模型求解

李 燚 唐 倩 刘联超 彭小刚 颜先洪

1.重庆大学机械传动国家重点实验室，重庆，4000442.重庆长安汽车股份有限公司，重庆，400023

0 引言

为了快速响应市场以及满足消费者多元化的需求，汽车主机厂商普遍采用按照订单生产的方式。具有“小批量、多品种、定制化”特点的订单使得混流生产模式受到主机厂商的青睐，即在一条生产线上同时生产多种类型的车辆。但混流生产使得汽车装配变得更加复杂，因为不同类型的车辆所需的零部件和对应的安装工具不尽相同，导致装配过程中每个工位针对不同车辆的安装作业时间及具体作业内容都会发生变化。如果不建立合理的生产调度模型，不仅难以发挥混流生产的优势，反而会降低生产效率，增加生产成本。

汽车混流装配属于一种典型的流水车间调度问题(flow shop scheduling problem，FSSP)，国内外学者针对该问题进行了深入研究，主要可归纳为调度模型的建立和多目标优化求解两个方面。针对流水车间调度模型，鲁建厦等[1]建立了最小化总调整时间和最小化空闲和超载时间的多目标优化模型。吴永明等[2]针对混流装配线建立了最小化装配线的生产节拍、站间平滑指数、演进平衡调整成本的调度模型。王炳刚等[3]深入研究了加工总切换时间最小化和零部件消耗平顺化的调度模型。唐秋华等[4]则以零部件消耗均衡化、工位作业位置精准化以及车型调整费用最小化为优化目标。赵燕伟等[5]考虑车间工件工序、装配工序等约束条件,以加工机器最小能耗为优化目标。DENG等[6]建立了最长完成时间和总延迟时间最小化的双目标优化模型。LI等[7]和LU等[8]均建立了最长完成时间以及能量消耗最小化的双目标优化模型。虽然上述调度模型具有一定的实际指导意义并解决了一些实际生产问题，但是并未考虑流水车间涉及大量的人工以及人机协同操作的情况，而这种情况在汽车混流装配过程中真实存在，且往往会导致加工滞后以及装配质量问题。

针对流水车间目标优化模型求解，目前广泛采用智能优化算法，如人工蜂群算法[1]、粒子群优化算法[2]、遗传算法[9]、候鸟优化算法[10]、果蝇优化算法[11]、粒子群优化算法[12]、灰狼优化算法[13]、鲸鱼优化算法[14]等，上述算法在求解相应的目标优化模型时均取得了不错的效果。近年来，蚁群算法[15]因其独特的正反馈求解机制受到不少学者的青睐，被应用于求解多目标优化问题，如ZUO等[16]使用蚁群算法求解云制造中的多目标优化问题，REED等[17]和KUMAR等[18]将其应用于车辆路径规划问题，PEREZ等[19]将其应用于求解无人机的轨迹，均取得了很好的结果。本文建立了瓶颈选装工位负载平衡化、考虑换装与提前作业时间的加工滞后次数最小化的分层序列双目标优化模型，并设计了一种改进蚁群算法进行求解，以解决汽车混流装配过程涉及大量人工以及人机协同操作而导致工位过载、整车装配质量无法得到保证的问题。

1 问题描述与建模

1.1 问题描述

汽车总装车间由一条主装配线和多条分装配线组成，其中分装线是为了将某些零件装配在一起形成部件总成，然后按照排产顺序同步输运送到主装配线上的特定工位与对应车辆进行装配，从而提高装配效率，如变速器分装线、底盘合装分装线、仪表分装线等。本文以主装配线为研究对象，在主装配线上，车辆通过滑撬或者吊具以一定的速度匀速通过流水线上各个工位，然后工位上的两边布置工人或者机器人进行相应的装配作业。由于总装车间的装配线大部分工位涉及人工操作以及人机协同工作，同时订单排产时最小生产循环中的生产车辆车型、配置不同，导致在装配流水线的每个工位不仅安装的零件种类、型号繁多，而且装配作业内容以及所耗费时间也不同。如果不建立合理的混流装配调度模型从而得到合适的生产序列，不仅难以保证生产线负荷平衡从而导致生产效率低下，更无法保证装配工艺造成整车装配质量参差不齐的情况。

1.2 模型的建立

首先对汽车混流装配过程作以下假设：①排产车辆序列一旦确定就不能中途任意更改，否则会导致分装线上的零部件总成和待装配车辆匹配错误，造成生产线停线；②边线的物料供应都可以按时送达，不会因物料供应问题而导致各工位上的装配任务暂停；③每个工位在同一时间内只能对一辆车进行加工作业。所建立的数学模型涉及的参数定义见表1。

表1 模型参数定义

1.2.1瓶颈选装工位负载平衡化模型

在混流装配流水线上存在某些瓶颈工位，如果该工位上连续多次装配某类型的选装件会导致负荷超载，即当前工位无法在规定时间内完成对应的装配工作，导致生产线停线，影响生产节拍，因此，需要对该工位某类选装件的连续装配次数做出限制(表1中rk∶sk)。以天窗选装件为例，车辆的配置中可分为全景天窗、普通天窗、无天窗三类。当装配的车辆无天窗时，该工位无需任何操作，处于闲置状态，但是该工位连续装配全景天窗时，会出现相关工位过载情况。针对全景天窗选装件的频次限制设定为2∶3(见表2)，即连续生产的3辆汽车中，选装全景天窗的车辆数目不能超过2。

表2 全景天窗安装频次限制

假设部分待生产序列(即对应的全景天窗选装情况)如表3所示。表中第2行值为0时，表示该对应序列位置的车辆不需要全景天窗选装件，即ov,k为0；当需要安装全景天窗时，ov,k为1，明显可知，序列中的2、3、4位置对应的3辆车超出了选装件频次限制。假设待装配的车辆集合为V，排好的生产序列为N，则两者应满足的关系为

(1)

其中，xv,n={0,1}，上式保证待装配的车辆在生产序列中只能且必须出现一次，符合流水装配线加工需求。选装工位的过载约束数学表达式[20]如下

(2)

∀k∈Opn=sk-1,sk,…,N

xv,n′∈{0,1}ov,k∈{0,1}

该问题属于典型汽车排序问题[21]，GENT[22]将其转化为哈密顿路径问题，TAMAS[23]将其转化为集合覆盖问题，从而证明其为NP-hard问题，即无法在多项式时间内求解。本文将其转化为优化模型，以便后文使用改进蚁群算法进行求解，具体表达式为

(3)

1.2.2最小化工位加工滞后次数模型

以待装配序列中位置为n的车辆在流水装配线工位m上完成相应的装配作业为例，涉及人工及人机协同操作的每个工位具体工作流程可分为以下两部分：

(1)准备过程。当完成上一个装配作业后，首先需要进行短暂的休息，然后通过查看工位旁的看板确定下一辆车所需的零部件类型，并从线边库存中挑选对应的零部件，最后调整或更换对应的装配工具。其中，休息时间和查看并挑选零件的时间为pm，为固定值。但若前后车辆在该工位所装配的零件不同时，则需要花费额外的时间an,m来切换或者调整安装工具，其表达式为

an,m=tm

(4)

其中，tm为更换或者调整安装工具所花的时间，与工位有关。当前后车辆装配的零件型号尺寸相同时，an,m=0。

(2)安装过程。操作工人完成当前工位所需的装配工作。假设车辆v在当前工位的安装时间为Cv,m，则在车辆序列中为n的车辆安装时间为

安装时间与工位以及安装的零件有关。所以装配所花费的时间为

传统的柔性流水车间调度问题(flexible flow shop scheduling problem, FFSP)中，n个订单在m个工位上加工，每个订单在各个工位上加工所需的时间di,j(i=1,2,…,n；j=1,2,…,m)不同，所以生产线的生产节拍应该满足的条件为

d≥maxdi,j

(5)

与传统流水线加工不同，在汽车混流装配流水线中，车辆通过滑撬或者吊具在流水线上以均匀的速度通过，每个订单在各个工位上加工所需的计划时间di,j(i=1,2,…,n；j=1,2,…,m)相同。所以d表示每个工位的生产周期，同时也表示混流装配线上的计划生产节拍。

在任意工位，前一辆车出现加工滞后情况时，为了满足生产要求，下一辆车的装配准备过程所需的时间pm会被压缩，使得工人没有足够的休息时间或者来不及做准备工作，从而影响车辆的装配质量。当处于汽车销售旺季时，生产节拍会达到甚至超过最大设定值，使得生产线处于超负荷运行状态，此时d会设置为更小的值，从而进一步压缩准备时间pm。

在实际生产过程中，与传统的流水车间调度模型不同的是工人操作比较灵活，在计划完工时间d内完工的情况下，可提前开始下一辆车的装配工作。提前时间与工位有关，设为Um。所以该车辆在工位m的加工装配滞后时间表达式为

(6)

其中，E1,m=0，明显可知En,m值为正表示当前工位的车辆加工滞后，Ev,m为负意味着当前工位作业提前完成。

举例说明，假设计划生产节拍d=60 s(本文默认的时间单位为秒)，Um=3 s，pm=8 s，更换夹具时间tm=5 s，部分生产序列中的车辆型号为{A,B,C,D,A,B,C,D},对应的安装时间为{52,50,44,45,52,50,44,45}，加上准备时间和更换夹具的时间后为{60,63,57,58,65,63,57,58}，对应的加工装配滞后时间为{0,3,0,-2,3,6,3,1}，明显可知该生产序列中有5辆车加工滞后。但若将生产序列中的车型更换为{A,C,B,C,B,D,D,A}，则加工装配滞后时间为{0,0,-3,0,-3,0,-3,-3}，没有车辆出现加工滞后情况，其中还有4辆车可以提前完成加工。所以，后者生产序列优于前者。车辆序列中的加工滞后次数统计表达式为

(7)

结合式(1)、式(3)和式(9)，最终本文所建立的分层序列双目标优化模型为

(8)

首先优化f1，然后在f1取得最优值(或者近似最优值)的解集合中确定f2取得最小值对应的解，即寻找满足f2取得最优值的同时满足f1也取得最优值的解。需要说明的是，选装件选项的分类和车型配置的分类并不完全相同，假设三种车型A、E、H选装件类型相同，如果得到的生产序列为{A,B,C,D,E,F,G,H}，则随意调换A、E、H的位置，f1的值保持不变，但是f2的值不尽相同。

2 改进的双目标蚁群算法介绍

2.1 基本原理

当前针对车间调度的优化问题往往采用智能启发式算法，如混合启发式算法[24]、遗传算法[25]。近年来蚁群算法[26]可有效地解决NP-hard相关的优化问题，尤其是旅行商、车间调度等问题，受到学术界和工业界的广泛关注。

本文针对分层序列双目标优化问题所设计的改进蚁群算法的求解思路为：将待生产的车辆视为一系列的节点，蚂蚁首先随机选择一个节点作为起始点，然后根据转移概率规则(信息素、启发式信息共同作用)逐一选择下一个节点，直至所有节点被选择完成，最终形成的节点序列即为所求的一个可行解。然后对可行解中的相邻节点进行信息素局部更新。当种群中所有蚂蚁完成上述操作之后，会存在多个可行解，构成一个解空间。在解空间中寻找最优序列，并将最优序列的相邻节点进行信息素全局更新。最优序列的判定规则如下：在当前解空间内，寻找优化目标函数一取得最优值的可行解，如果存在多个目标函数一取得最优值的可行解，则选择其中满足优化目标函数二取得最优值的解。通过不断的迭代，最终得到全局最优解或者近似最优解。算法具体流程见图1。

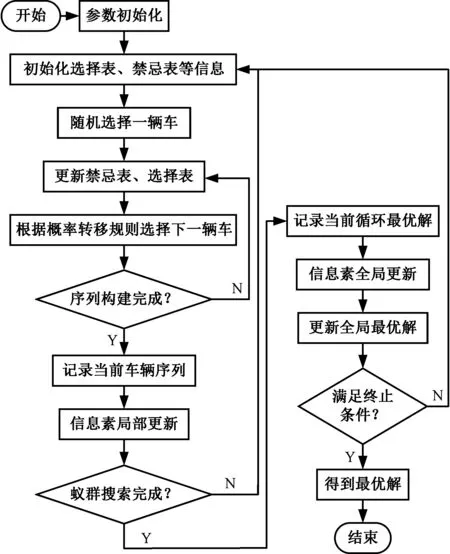
图1 改进蚁群算法流程图Fig.1 Improved ACO algorithm flow chart

2.2 算法参数定义

本文设计的改进蚁群算法涉及的参数定义见表4。

表4 算法参数定义

2.3 信息素更新

τu,v表示车辆u和v之间的信息素，而信息素更新过程分为局部更新和全局更新。当每只蚂蚁构建完成一个可行解即车辆生产序列之后，对该序列中的相邻节点进行信息素局部更新，局部更新表达式为

τu,v(t)=ρlτu,v(t)+(1-ρl)τ0

(9)

其中，ρl取值范围为[0,1]，τ0为信息素浓度初始值。局部实时更新的目的是减少已选择节点之间的信息素浓度，避免之后的其他蚂蚁做出同样的决策，从而保持了选择的多样性，避免陷入局部搜索。

当种群中所有的蚂蚁构建完成可行解，形成一个解空间，然后确定当前解空间中最优可行解。最优解的具体评价方式为：首先寻找在当前解空间中第一优化目标取得最优值的序列，如果存在多个序列，则在其中寻找第二优化目标取得最优值的序列。然后对该序列中的相邻节点进行信息素全局更新，更新表达式为

τu,v(t+1)=ρgτu,v(t)+(1-ρg)τu,v(t)

(10)

其中，ρg取值范围为[0,1]，而τu,v(t)的表达式如下：

(11)

式中，f1、f2分别为当前解空间中最优可行解所对应的第一优化目标和第二优化目标函数的值。

通过全局更新规则，可保证将当前循环中最优序列的整体信息反映到信息素上，指导后续搜索过程，形成正反馈机制。

2.4 概率转移规则

假设某只蚂蚁在构建可行解过程中，当前已有序列中的最后一个辆车为u，然后从待排序的车辆集合alist中选择下一辆车v，转移概率规则如下：

(12)

其中，q0为[0,1]区间的参数，q为[0,1]区间均匀分布的随机数，su,v的具体表达式为

(13)

其中，nv,1和nv,2分别为在已有车辆序列中添加车辆v之后的优化目标函数一和目标函数二的变化值。当q>q0时，计算待排序中每辆车的选择概率，然后采用轮盘赌方法选择车辆v。概率计算公式为

(14)

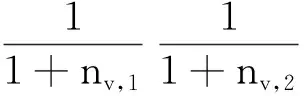
(15)

式中，xv,k为常数0或1，表示当前车辆是否有选装件k；Uk为选装件k在剩余待排序的车辆的占比。

该算法具有以下优点：①该算法整个过程为正反馈机制，从而使得搜索过程不断收敛并逼近最优解；②加入启发式规则后有效地克服了传统蚁群算法容易陷入局部最优的问题；③概率转移规则中加入选装件加权占比规则，可使第一优化目标得到快速的收敛。

3 仿真实验及结果

3.1 仿真实验

以某主机厂的总装车间为例，混流装配过程每个最小生产循环中共36辆车，其中共有9种不同的车型配置(用字母A～I表示)，每种车型配置有4辆车。主装配线上选取3个典型的瓶颈选装件，对应的频次限制以及每种车型配置对应的选装情况见表5。其中，数字0代表对应的车辆未装配相应的选装件；数字1代表需要装配对应的选装件。

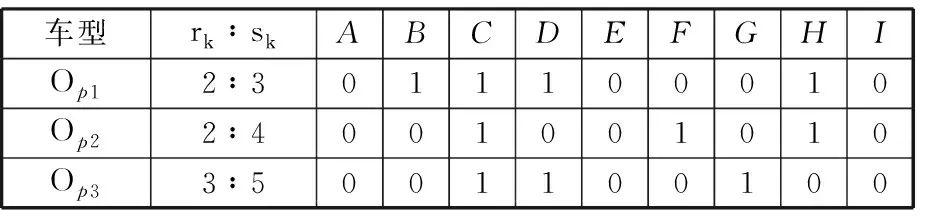
表5 车型瓶颈选装件

同时选取流水装配线上的某8个连续安装工位为例，车辆在各个工位上的装配作业所需的安装时间见表6，车辆在各个工位所需的工具类型见表7。

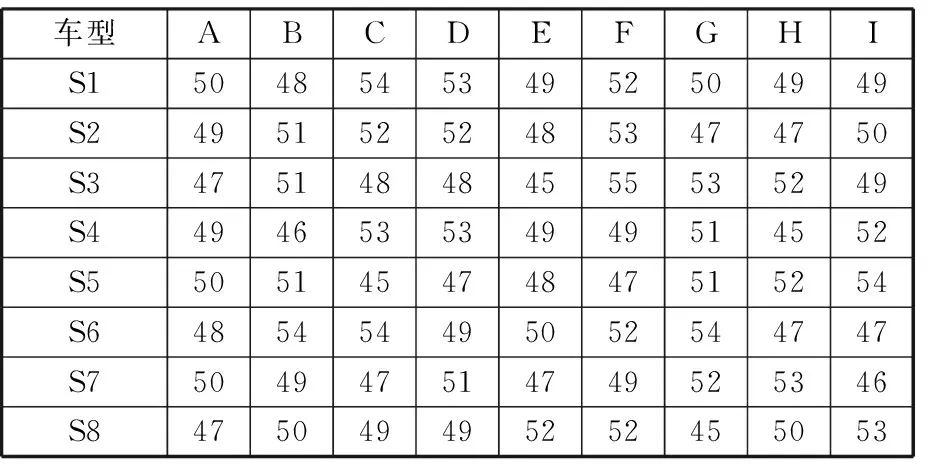
表6 工位安装时间

需要说明的是，表7不同工位中相同的数字并不代表相同的安装工具，该罗马数字用于说明在单个工位中各种类的车辆是否使用不同的工具。各个工位调整工具的时间见表8。

表7 工位安装所需工具型号

表8 工位切换工具时间

生产节拍d=60 s，各个工位提前装配作业时间U=3 s，准备时间p=6 s。实验过程中改进蚁群算法的参数取值见表9。

表9 算法参数取值

3.2 实验结果

将本文采用的改进蚁群算法和传统蚁群算法、对比遗传算法[26]各计算10次，并记录迭代过程中的优化目标函数值以及最优解。目标函数一在前10次迭代过程中的平均值变化情况如图2所示，最优解对应的目标函数一的取值如图3所示。同理，在整个迭代过程中，目标函数二在迭代过程中平均值的变化情况如图4所示，最优解的目标函数二的变化情况如图5所示。

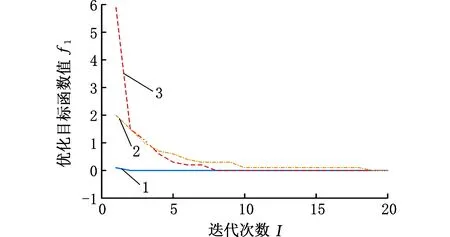
1.改进蚁群算法 2.对比遗传算法 3.传统蚁群算法图2 目标函数一的收敛曲线平均值Fig.2 Mean value of convergence curve of objectivefunction one

1.改进蚁群算法 2.对比遗传算法 3.传统蚁群算法图3 最优解对应的目标函数一的收敛曲线Fig.3 Convergence curve of the objective functionone corresponding to the optimal solution

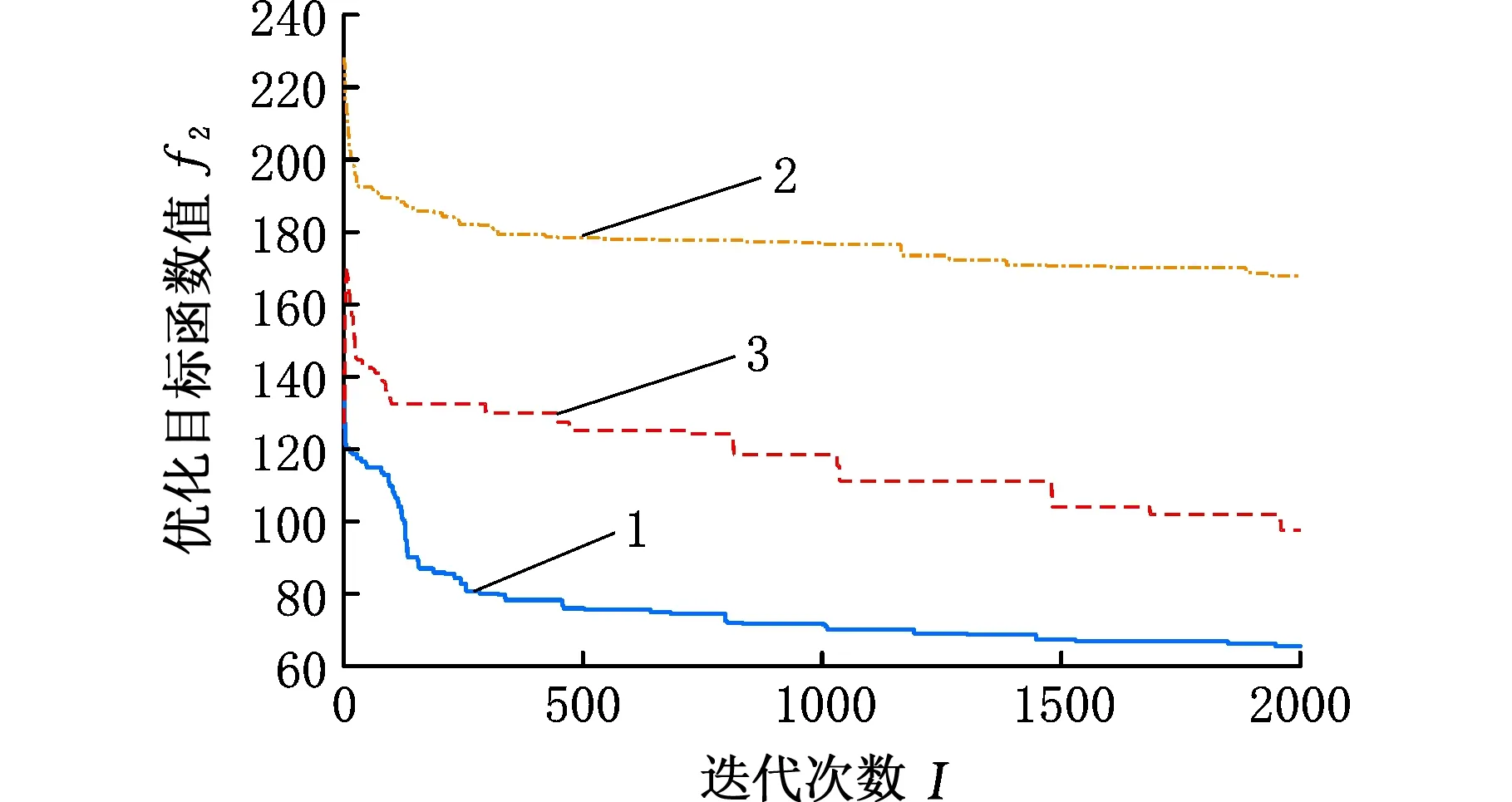
1.改进蚁群算法 2.对比遗传算法 3.传统蚁群算法图4 目标函数二的收敛曲线平均值Fig.4 Mean value of convergence curve of objectivefunction two

1.改进蚁群算法 2.对比遗传算法 3.传统蚁群算法图5 最优解对应的目标函数二的收敛曲线Fig.5 The convergence curve of the objective functiontwo corresponding to the optimal solution

由图2、图3可知，在优化第一目标函数过程中，即瓶颈选装工位负载平衡化时，相比传统蚁群算法，使用改进蚁群算法收敛得更快；由图4、图5可知，在优化第二目标函数过程中，即最小化工位加工滞后次数时，本文算法不仅收敛得更快，而且收敛的效果也更好。具体统计结果见表10。

当设定不同的计划生产节拍时，使用本文所设计的改进蚁群算法计算10次之后求解得到的各个目标函数的最优值和平均值见表11。由表11可知，当计划生产节拍设定时间大于或等于63 s时，可保证瓶颈选装工位负载平衡化以及考虑换装与提前作业时间的加工滞后次数为0，从而保证了整车装配质量。

表10 实验结果对比

表11 不同的计划生产节拍对应的优化目标值

4 结论

(1)本文面向汽车混流生产模式下的流水装配线，为了保证生产节拍以及整车装配质量，建立了瓶颈选装工位负载平衡化和考虑换装与提前作业时间的工位加工滞后次数最小化的分层序列双目标优化模型。

(2)设计了一种改进的蚁群算法用于求解所建立的优化模型。为了快速优化瓶颈选装工位负载平衡化目标，添加选装件加权占比启发式规则；为了保证所求的解不但使第一优化目标函数取得最优值，而且使得第二优化目标也取得最优值，设计一种特殊的启发式函数用于转移概率计算以及信息素全局更新，同时更改最优解的评价方法。

(3)采用某汽车主机厂实际生产相关数据进行仿真实验，验证了本文算法和模型的有效性；此外，该算法可以反向求解在瓶颈选装工位负载平衡化目标函数取得最优值的情况下工位加工滞后次数为0的计划生产节拍，具有一定的生产指导意义。