考虑不定拆卸程度的选择性异步并行拆卸序列规划
2021-05-19王振东杜百岗李益兵
郭 钧 王振东 杜百岗 李益兵
1.武汉理工大学机电工程学院,武汉,4300702.武汉理工大学湖北省数字制造重点实验室,武汉,430070
0 引言
拆卸过程作为废旧(end-of-life,EOL)产品再生过程中的关键步骤,其规划问题逐渐受到了人们的广泛关注。拆卸序列规划(disassembly sequence planning,DSP)是指根据预定的评价指标,确定EOL产品中零部件的最佳拆卸顺序。在工程实践中,EOL产品拆卸过程主要是对高剩余价值或有害的零部件进行提取。选择性并行拆卸具有拆卸步骤少、拆卸时间短、拆卸能耗低等优点,对提高EOL产品的再生效率具有重要意义。本文针对复杂EOL产品再生的拆卸过程,研究不定拆卸程度的选择性异步并行拆卸序列规划方法,从而达到提高拆卸收益及拆卸效率的目的。
近年来,选择性并行拆卸受到了国内外学者的广泛关注。SMITH等[1]利用模块化理论将产品分组为模块并通过递归规则进行并行拆卸。KIM等[2]建立了成本顺序依赖选择性并行拆卸序列整数规划模型,以拆卸成本最小为优化目标,用分支定界算法进行求解。PISTOLESI等[3]建立了选择性并行拆卸序列规划模型并设计了多目标张量模因算法进行规划求解。田永廷等[4]提出了以拆卸总时间最小为目标的基于遗传算法的选择性并行拆卸序列规划方法。上述文献考虑的并行拆卸通常为同步并行DSP,将并行任务分步骤进行,每一步的并行任务必须同时开始,而在实际拆卸过程中,在满足约束关系的前提下拆卸任务可无需等待直接开始执行。为缩短同步等待时间,REN等[5]提出了异步并行拆卸的概念,建立了异步并行拆卸序列规划模型,并利用遗传算法进行优化求解,证明了异步并行拆卸较同步并行拆卸效率更高。邓明星等[6]在异步并行拆卸的基础上提出了考虑多目标件的异步并行拆卸序列规划方法,以拆卸完工时间最小为优化目标,利用改进的遗传算法进行求解,证明了该方法的可行性与有效性。然而现有的选择性并行拆卸通常是以目标件为出发点逆向搜索出产品的必拆零件集合,从而将选择性拆卸序列规划问题转化为定拆卸程度的局部完全拆卸序列规划问题。该拆卸方式应用于EOL产品的再生过程中,忽略了必拆零件集合以外的非必拆零部件的再生收益。因此,本文在此基础上提出将目标件逆向搜索出的必拆零件集合作为EOL产品的最少拆卸件集合,进一步考虑EOL产品所有零部件再生收益的不定拆卸程度的选择性异步并行拆卸方法。
并行拆卸序列规划问题复杂,随着EOL产品零件数量增加,拆卸序列解空间呈指数增长,传统的拆卸序列规划方法已无法满足复杂产品拆卸需求。于是许多学者利用智能算法来解决该问题。目前应用到DSP问题上的智能算法有遗传算法[7]、蚁群算法[8]、人工鱼群算法[9]、人工蜂群算法[10]、花朵授粉算法[11]等。生物地理学优化(biogeography-based optimization,BBO)算法是由SIMON[12]受到生物地理学理论的启发而提出的,该算法借鉴生物地理学中的物种迁移模型来求解优化问题,具有算法结构简单、局部开发能力强等诸多优势,目前BBO算法在工程优化[13]、车间调度[14]等领域取得了明显的效果,具有十分广阔的应用前景。DSP问题是一个NP-hard问题[15],目前将BBO算法用于求解DSP问题还鲜有报道。
综上所述,本文基于异步并行拆卸概念,提出了一种全面考虑废旧产品所有零部件再生收益的不定拆卸程度的选择性异步并行拆卸序列规划方法。针对该问题通过目标件逆向搜索确定最小拆卸程度,以拆卸时间最小与利润最大为优化目标,构建多目标异步并行拆卸序列规划数学模型。结合DSP问题特点,将原适用于解决连续优化问题的BBO算法进行离散化,并采用基于随机拓扑结构的迁移操作提高算法搜索能力,设计了多目标随机拓扑结构生物地理学优化(multi-objective random topology biogeography-based optimization,MRTBBO)算法进行求解。最后通过实例验证不定拆卸程度选择性异步并行拆卸方法的优越性及MRTBBO算法求解该模型的有效性。
1 模型的构建
1.1 不定拆卸程度选择性异步并行拆卸问题描述
EOL产品再生的拆卸过程目的是在尽可能少的时间内获取EOL产品中尽可能多的价值。考虑到有害零部件的强制拆卸处理以及拥有高剩余价值的零部件的拆卸需求,需将这些零部件作为选择性拆卸中的目标件。而传统的选择性拆卸多是指定程度的拆卸序列规划问题,图1中红色圆代表目标件,黄色圆代表目标件逆向搜索出的优先拆卸件。图1a所示为将其转化为定拆卸程度的局部完全性拆卸。而不定拆卸程度的选择性拆卸的拆卸程度在一个范围之间,如图1b所示,其中虚线围住部分代表最小拆卸件集合,实线围住部分为其最大拆卸件集合。
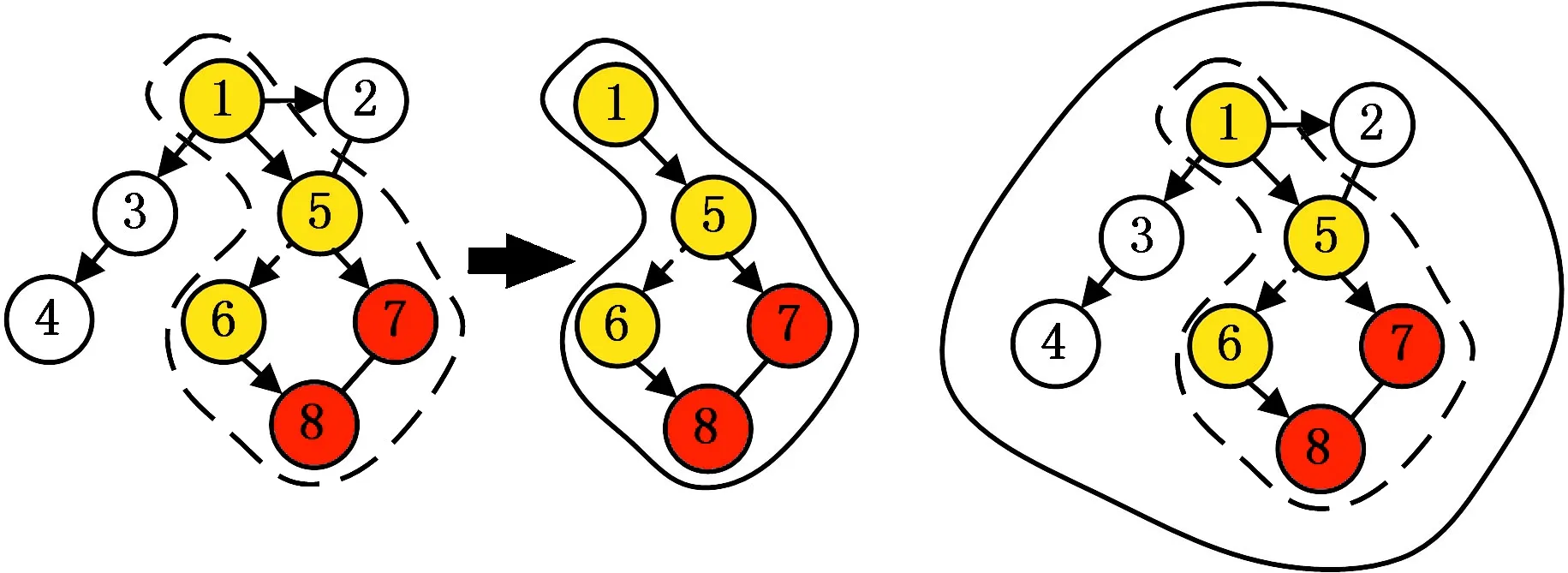
(a)定拆卸程度 (b)不定拆卸程度图1 选择性拆卸的拆卸范围对比Fig.1 Comparison of disassembly range forselective disassembly
图1示例零件的拆卸时间与收益见表1。在异步并行拆卸模式下,图1示例的定拆卸程度的选择性拆卸与不定拆卸程度的选择性异步并行拆卸的解如图2、图3所示,图中M1、M2表示EOL产品。在考虑EOL产品每个零部件的拆卸时间与拆卸收益的情况下,对比图2、图3a,不定拆卸程度选择性异步并行拆卸能在相同的拆卸时间8.5 s下比定拆卸程度的选择性异步并行拆卸多拆卸2、3号零件,从而获得更多收益,或进一步延长拆卸时间至9 s(图3b),执行更多的拆卸操作,获取更大的收益。

表1 拆卸时间与收益
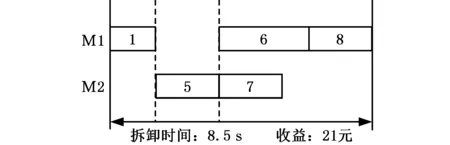
图2 定拆卸程度的选择性异步并行拆卸Fig.2 Selective asynchronous parallel disassemblywith a certain degree of disassembly

(a)拆卸时间8.5 s(b)延长拆卸时间至9 s图3 不定拆卸程度选择性异步并行拆卸Fig.3 Selective asynchronous parallel disassemblysolution set with indeterminate degree of disassembly
综上可见,在EOL产品再生过程的拆卸中,有必要在考虑拆卸目标件的基础上进一步考虑EOL产品的所有零部件拆卸收益,建立以拆卸时间最小、拆卸收益最大为目标的不定拆卸程度选择性异步并行拆卸模型。
1.2 拆卸混合图模型
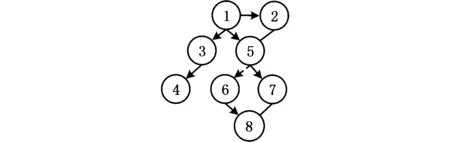
图4 拆卸混合图示例Fig.4 Example of disassembling hybrid diagram
拆卸混合图是用来描述产品零部件之间的连接关系以及约束关系的表达模型,能充分表达出产品的拓扑结构。本文采用拆卸混合图来表达待拆卸产品的信息。如图4所示,将拆卸混合图定义为G={V,UE,DE,IE},其中,V为拆卸混合图的最小拆卸单元的集合,UE为拆卸混合图的无向边集合,DE为有向实线边集合,IE为有向虚线边集合。V={v1,v2,…,vn},n为最小拆卸单元个数;UE={u1,u2,…,um},m为无向边的总数,无向边表示两最小拆卸单元之间存在接触关系;DE={d1,d2,…,dk},k为有向实线边的总数,有向实线边表示两最小拆卸单元之间既存在接触关系又存在拆卸优先关系;IE={i1,i2,…,ih},h为有向虚线边的总数,有向虚线边表示两最小拆卸单元之间只存在拆卸优先关系。
为便于计算机对拆卸混合图模型进行表达和优化分析,将拆卸混合图做数字化处理。将拆卸混合图转化为接触约束矩阵Mc和优先约束矩阵Mp:
则由Mc与Mp的定义可知,任意时刻拆卸单元i的可拆条件为
(1)
1.3 问题假设
为了简化问题,做以下假设:①假设零部件基本拆卸时间与拆卸收益为定值,不受质量状态影响,即本文不考虑不确定质量状态所带来的基本拆卸时间与收益的波动;②假设拆卸资源充足且不存在拆卸过程中的空间干涉问题。
1.4 模型相关参数及说明
模型相关参数定义见表2。
目标函数为
(2)
(3)
约束条件为
(4)
(5)
(6)
xi=1 ∀i∈Cm
(7)
(8)
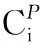
(9)
(10)
(11)
目标函数式(2)为拆卸过程总时间,即并行拆卸过程中最后一个零件的拆卸结束时间;目标函数式(3)为拆卸过程总收益,其中包含零部件的预期再生收益以及与并行数和总时间相关的拆卸成本;约束式(4)表示零件i的开始拆卸时间为
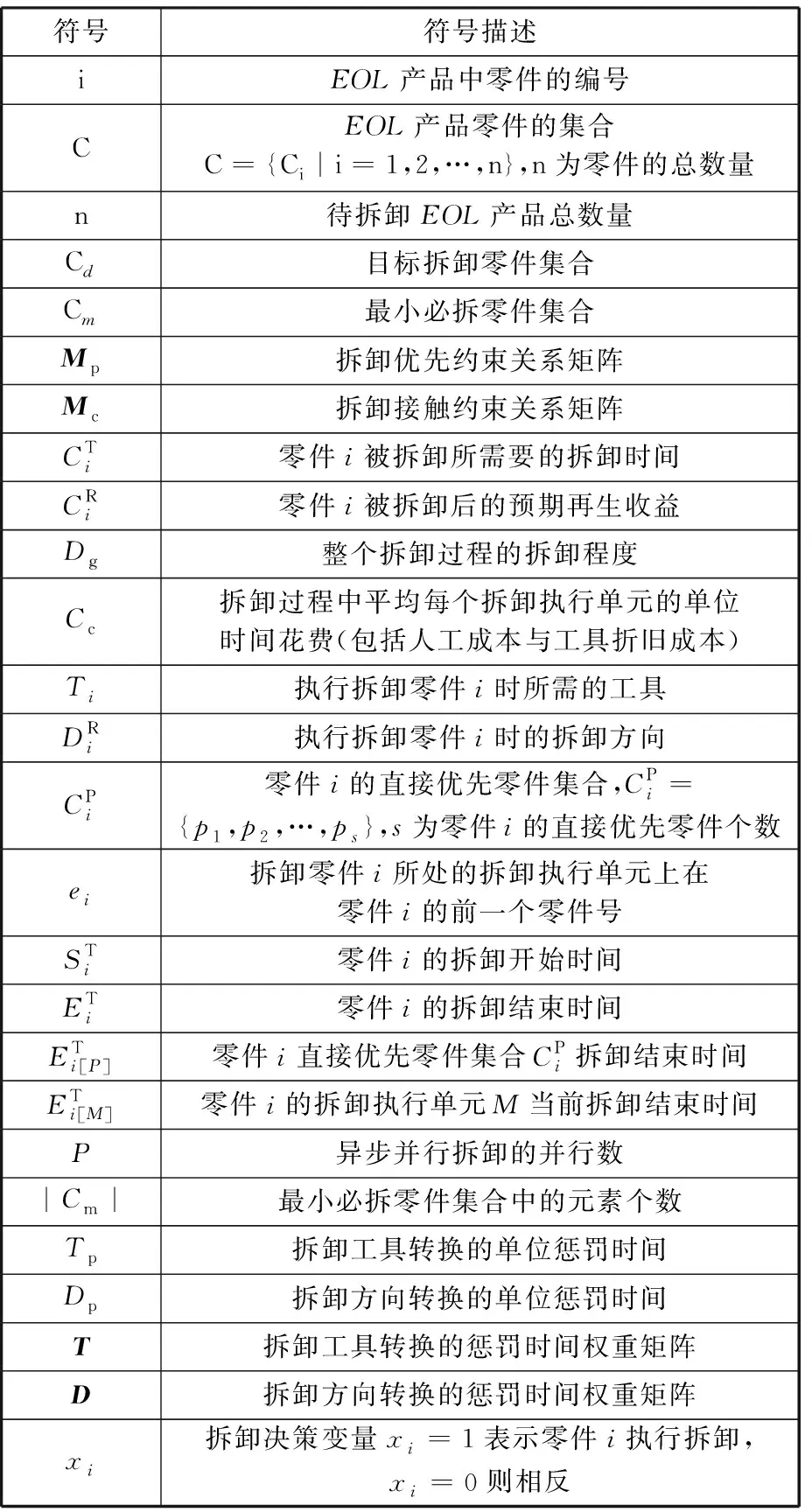
表2 符号定义
其直接优先零件集合拆卸结束时间与零件i执行单元M当前拆卸结束时间之间的最大值;约束式(5)表示零件i的直接优先零件集合的拆卸结束时间为其优先零件拆卸结束时间中的最大值;约束式(6)表示拆卸零件i的执行单元M的当前结束时间为拆卸其前一零件ei的结束时间;约束式(7)表示最小必拆零件集合中的零件必须拆卸;约束式(8)表示总的拆卸零件数量大于或等于最小必拆零件的数量;约束式(9)表示若零件i需拆卸,则其直接优先零件集合中的零件也需拆卸;约束式(10)表示零件i的拆卸结束时间需大于拆卸开始时间;约束式(11)用于计算拆卸序列的拆卸程度。
2 基于多目标随机拓扑结构生物地理学求解算法
BBO算法通过模拟岛屿之间的物种迁徙从而达到生态平衡的迁移机制与栖息地自然灾害的突变机制来求解优化问题。栖息地适应物种生存的程度用适应度指数(habitat suitability index,HSI)来衡量。高HSI值的栖息地拥有较高的迁出率与较低的迁入率,而低HSI值的栖息地拥有较低的迁出率与较高的迁入率。栖息地物种的迁入迁出机制使HSI值较低的栖息地可通过获得HSI值高的栖息地提供的优秀物种变量(suitability index variables,SIV)改善自身。此外,BBO算法的突变机制使栖息地上的SIV发生突变,从而使得BBO算法具有一定的防止陷入局部最优的能力。
原始的BBO算法是用来解决连续优化问题的,本文针对问题模型将BBO算法离散化加以改进从而提出了MRTBBO算法,以解决本文所提的不定拆卸程度的选择性异步并行拆卸问题。
2.1 待拆卸零件搜索算法
本文在目标驱动推理法[16]的启发下提出一种待拆卸零件搜索算法。通过拆卸混合图的约束关系,输入目标件进行逆向递归搜索待拆卸零件集合。算法具体步骤如下:
(1)初始化搜索集合St1、被动件集合St2、待拆卸零件集合F为空,加载目标件集合S,加载接触约束矩阵Mc、优先约束矩阵Mp。
(2)将S中所有拆卸零件放入搜索集合St1与待拆卸零件集合F。
(3)判断搜索集合St1是否为空,为空则跳转至步骤(5);若St1不为空则以搜索集合St1中的零件作为主动件(被约束节点),依据可拆条件式(1)逆向推理出搜索集合St1中所有零件的被动件(直接优先约束节点)并放入St2。
(4)判断St2是否为空,为空则跳转至步骤(5);否则将St2去重后添加到待拆卸零件集合F中,并用St2替换搜索集合St1使之成为新的搜索集合St1,返回步骤(3)。
(5)将待拆卸零件集合F去重后输出。
2.2 栖息地编码
有效的编码方式可以减少算法中的不可行个体的生成,从而避免算法中对不可行个体的筛选与转化。本文结合不定拆卸程度选择性异步并行拆卸序列规划的特点,采用三层链表结构的编码方式:P={PRw,PRx,PRm},第一层PRw采用长度为n的1~n之间随机不重复整数序列来表示零件的拆卸权重,即PRw={w1,w2,…,wn},wi(i=1,2,…,n)代表零件i的拆卸权重。第二层PRx由长度为n的随机0-1二进制序列来代表是否拆卸,即PRx={x1,x2,…,xn},xi(i=1,2,…,n)为1表示零件i需拆卸,为0则表示不拆卸。第三层PRm由1~P之间的随机可重复整数来表示执行该零件拆卸的执行单元序号,即PRm={M1,M2,…,Mn},Mi(i=1,2,…,n)代表零件i由拆卸执行单元Mi执行拆卸操作。P为并行拆卸的并行数。图4示例的拆卸并行数为3的一段随机初始化编码见表3。
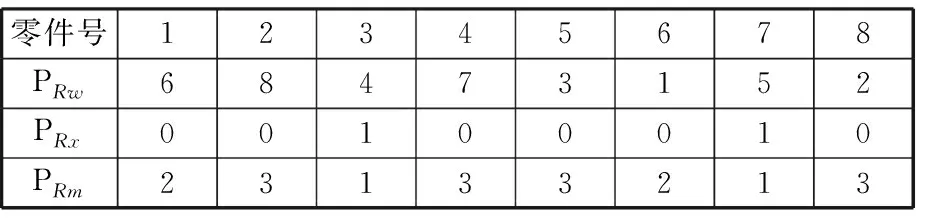
表3 栖息地初始化编码示例
2.3 栖息地解码
假定图4所示拆卸示例的目标件为{8},配合表3所示初始化编码,PRx中需拆卸的零件{3,7}与目标件{8}取并集为{3,7,8}。通过待拆卸件搜索算法获取最终需拆卸零件集合Df={1,3,5,6,7,8}。将初始栖息地编码的第二部分PRx序列进行调整,调整结果见表4,具体步骤如下:
(1)更新混合图模型中的接触约束矩阵Mc和优先约束矩阵Mp。在Mc与Mp中将最终拆卸零件集合Df以外的行与列剔除。
(2)结合Mc与Mp,依据可拆卸条件式(1)推断出当前可拆卸零件集合Dk={k1,k2,…,km}。
(3)从Dk中选出拆卸权重w最大的零件ki,使其在执行单元Mki上进行拆卸。
(4)更新Mp与Mc,将零件号ki所在列与行的值置0,解除与其相关的约束。
(5)判断最终所需拆卸零件集合Df中的零件是否都已拆卸,若未拆卸完则跳转至步骤(2),否则算法结束,输出最终拆卸序列结果。
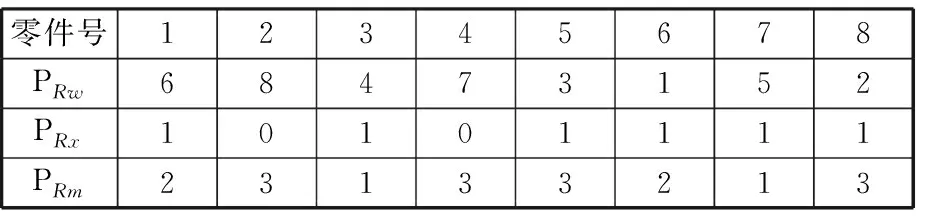
表4 栖息地编码调整
如表4所示,调整过后的编码按上述算法解码得出的最终拆卸序列结果为
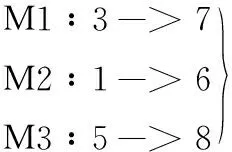
上式表明3个并行的拆卸执行单元的拆卸任务序列。
2.4 栖息地迁移机制
迁移机制是BBO算法的主要机制,迁移操作中包括迁入与迁出,该过程依据个体的迁入率与迁出率来进行选择并执行。迁入迁出率的确定方式不同也会导致算法性能的差异。
2.4.1计算迁移率
不同的迁移率模型对算法的优化性能产生重要影响,针对DSP问题的特点,本文采用正弦迁移模型来计算栖息地的迁入迁出概率,其迁入率λi与迁出率μi的计算公式如下:
(12)
(13)
其中,I为栖息地最大迁入率,E为栖息地最大迁出率,Hi为栖息地i的适应度指数,Hmax为所有栖息地中的最大适应度指数。在本文所提模型中,令I=E=1。
2.4.2迁移过程
确定栖息地的迁移概率后,需依据迁入迁出率来选择迁入迁出栖息地并执行迁移策略。本文按迁入迁出率的大小采用轮盘赌的方式依次选择被迁入栖息地Zi与迁出栖息地Zj。本文针对三层链表编码形式分别对权重序列PRw、是否拆卸序列PRx、执行单元序列PRm采取不同的迁移策略。
如图5所示,对于PRw序列,将零件总数n以内的正整数随机划分为两个集合W1与W2,被迁入栖息地Zi中的PRw序列在W1集合中的元素所在位置保持不变,依次填入临时栖息地Zk。然后将迁出栖息地Zj在W2集合的元素按照顺序依次填入临时栖息地Zk的空位,形成新的P′Rw序列。

图5 PRw序列的迁移操作Fig.5 PRw sequence migration operation
如图6所示,对于PRx、PRm序列,首先生成一串长度为n的随机0-1数组作为参照,其中元素为1指示栖息地Zi中对应位置的元素填入临时栖息地Zk的对应位置,元素为0指示栖息地Zj中对应位置的元素填入临时栖息地Zk的对应位置,从而形成新的P′Rx、P′Rm序列。
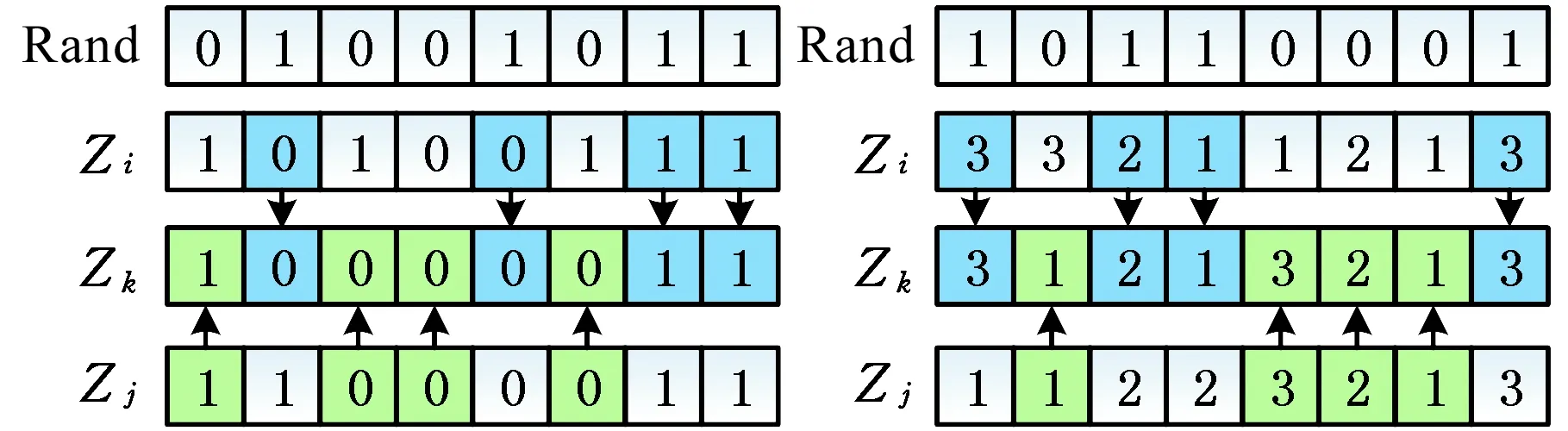
(a)PRx序列迁移(b)PRm序列迁移图6 PRx、PRm序列的迁移操作Fig.6 PRx、PRm sequence migration operation
PRw序列、PRx序列、PRm序列的迁移操作分别执行完毕后进行整合,{P′Rw,P′Rx,P′Rm}成为新栖息地,替换被迁入栖息地Zi,完成一次迁移操作。
2.4.3基于随机拓扑结构的迁移
BBO算法虽然具有多种优良性能,但是BBO算法的全局搜索性能还有所欠缺,容易陷入局部最优。为了提高BBO算法的搜索性能,本文采用基于随机拓扑结构的迁移算子。
BBO的迁移算子默认是全局拓扑结构,即每次迁移操作中的迁出解从全体栖息地中依据迁出率选择进行迁移,而随机拓扑结构为每个栖息地都随机生成一个大小不定的邻域范围,为该栖息地选择迁出栖息地时迁出解均从中按迁出率进行选择。此外,用平均邻域大小参数K来设置种群中所有栖息地的平均邻域水平。设置参数Nmax为外部档案集质量无改善的迭代次数上限,当算法连续Nmax次迭代寻优后外部档案集质量无改善时,将种群的随机拓扑结构进行重置。这种机制有助于算法跳出局部最优。
2.5 栖息地突变机制
自然界中发生重大灾害会导致栖息地的组成和结构发生急剧变化,BBO算法将该情形模拟成栖息地突变机制,栖息地的突变机制也是BBO算法至关重要的环节,可以用来提高种群的多样性。
2.5.1计算突变率
栖息地的突变率与栖息地的物种数量概率成反比,物种数量较多或较少时的物种数量概率都相对较低,而物种数量为中等水平的概率比较高。结合拆卸序列规划问题,本文提出了一种基于适应度指标的突变机制,即在适应度较低和较高的栖息地中的突变概率相对较低,而适应度接近于平均适应度时的突变概率相对较高。本文的突变概率计算公式为
(14)
2.5.2突变过程
结合三层链表的编码方式,拆卸权重序列PRw与是否拆卸序列PRx及执行单元序列PRm分别采取不同的突变方式,如图7、图8所示,PRw序列的突变方式是从PRw序列上随机选择一个位置上的元素插入其他位置;PRx序列的突变方式是从PRx序列上随机选择两个位置的元素进行二进制取反;PRm序列的突变方式是从PRm序列上随机选择两个位置的元素随机改变成其他执行单元序号。

图7 PRw序列的突变方式Fig.7 Mutation of PRw sequence

(a)PRx序列突变 (b)PRm序列突变图8 PRx、PRm序列的突变方式Fig.8 Mutation of PRx,PRm sequence
2.6 算法流程
综上所述,给出的算法流程图见图9。
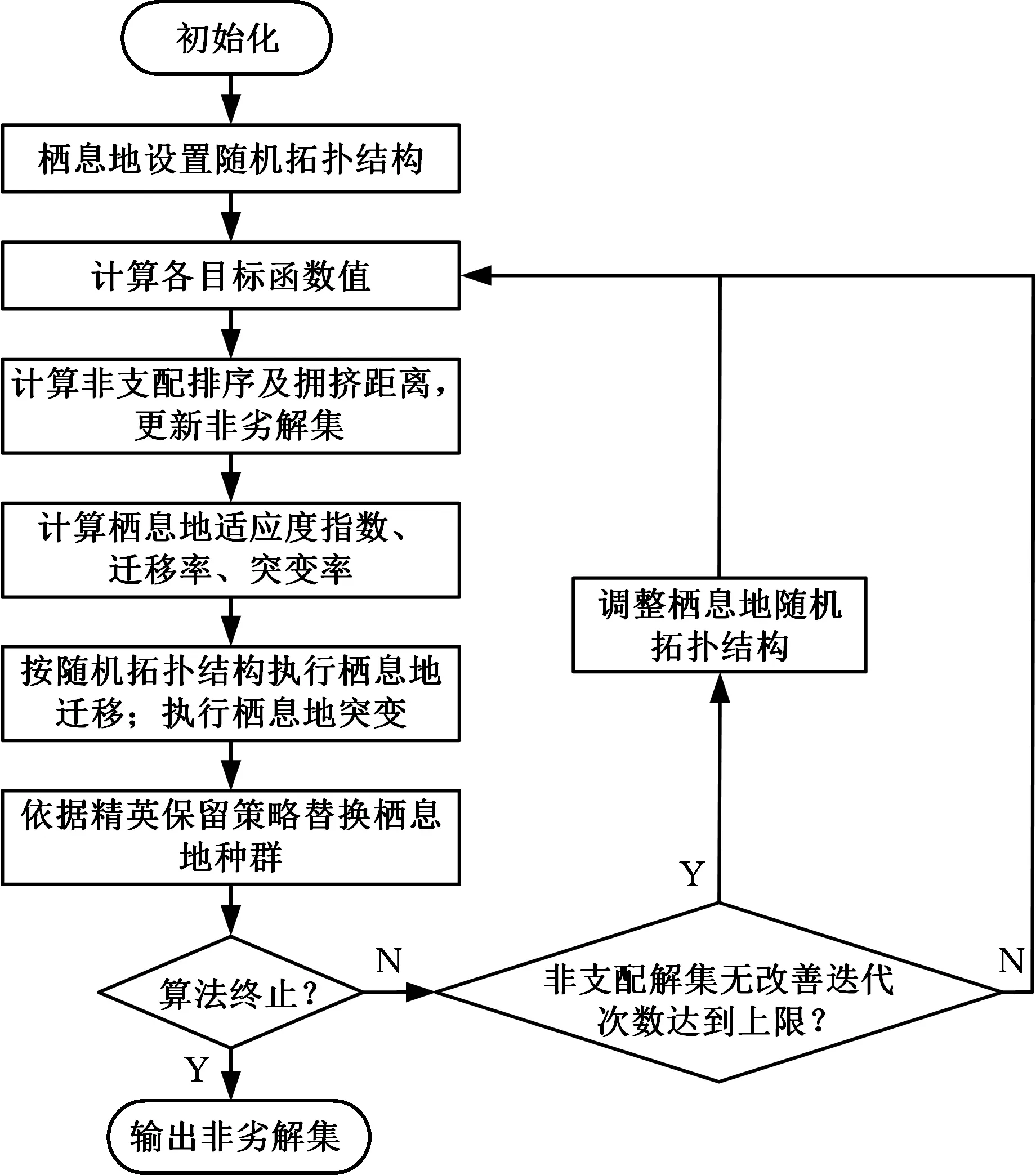
图9 算法流程图Fig.9 Algorithm flow chart
3 实例应用
为了验证本文所提模型方法的优越性和所提算法求解该模型问题的有效性,利用MATLAB平台编写了MRTBBO算法,算法的运行环境为2.6GHz CPU,12G RAM,Windows 10 64位操作系统的个人计算机。
3.1 试验案例
本文分别采用两种不同规模大小的试验案例来验证所提模型的优越性。案例一是零件数为23的机械臂[17];案例二是零件数为52的二级圆柱圆锥减速器,其三维模型爆炸图见图10,拆卸混合图见图11,零件信息表见表5。
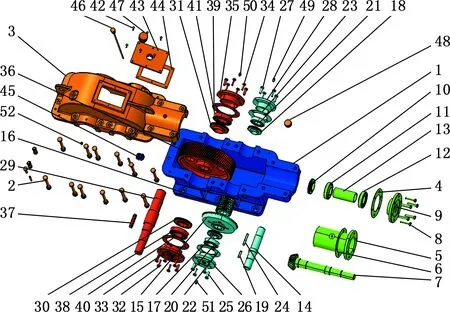
图10 案例二:二级圆柱圆锥齿轮减速器Fig.10 Case 2: two-stage cylindrical bevelgear reducer
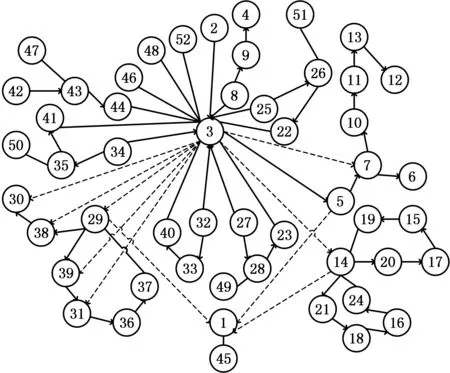
图11 案例二:二级圆柱圆锥齿轮减速器拆卸混合图Fig.11 Case 2: disassembly hybrid diagram oftwo-stage cylindrical bevel gear reducer

表5 案例二:二级圆柱圆锥齿轮减速器零件信息
3.2 试验结果分析
本文通过正交试验确定MRTBBO算法分别作用在两个试验案例上的最优参数。
3.2.1案例一
算法参数设置:种群大小Psize=250,迭代次数Gmax=800,栖息地最大突变率Pmax=0.2,平均邻域大小K=6,非支配解集无改善迭代次数上限Nmax=10。针对本文所提不定拆卸程度选择性异步并行拆卸问题,设目标件Cd={1,6,12},并行度为3,计算结果Pareto解空间分布如图12所示,其中各个解的详细拆卸序列见表6。作为对比设置同样的目标件、并行度,传统定拆卸程度下的选择性异步并行拆卸优化结果见表7。不定拆卸程度模式非支配解集表6中案例一的拆卸甘特图见图13a,定拆卸程度模式最优解的拆卸甘特图见图13b。
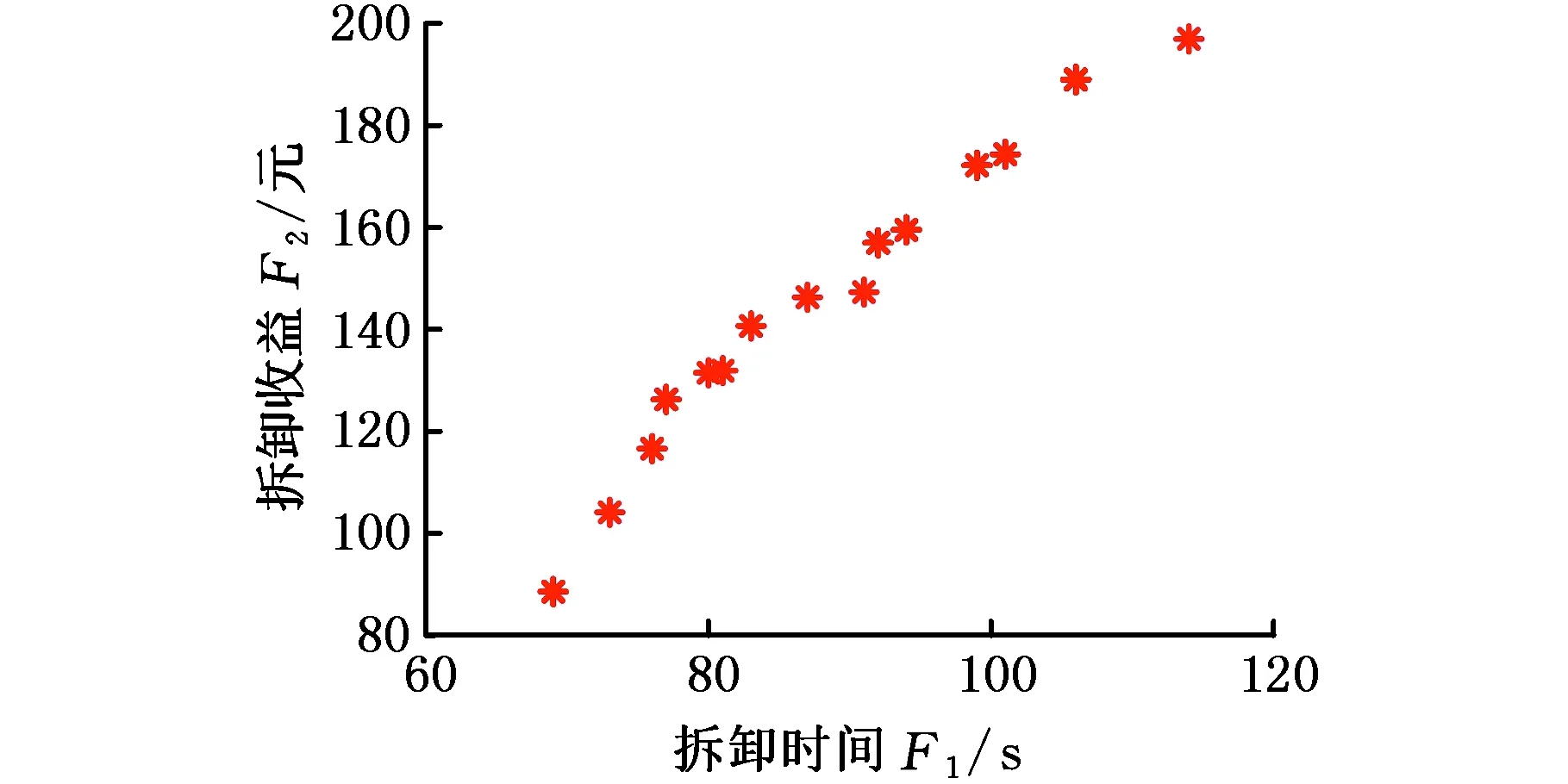
图12 案例一:Pareto解集空间分布Fig.12 Case1: spatial distribution of Paretosolution set
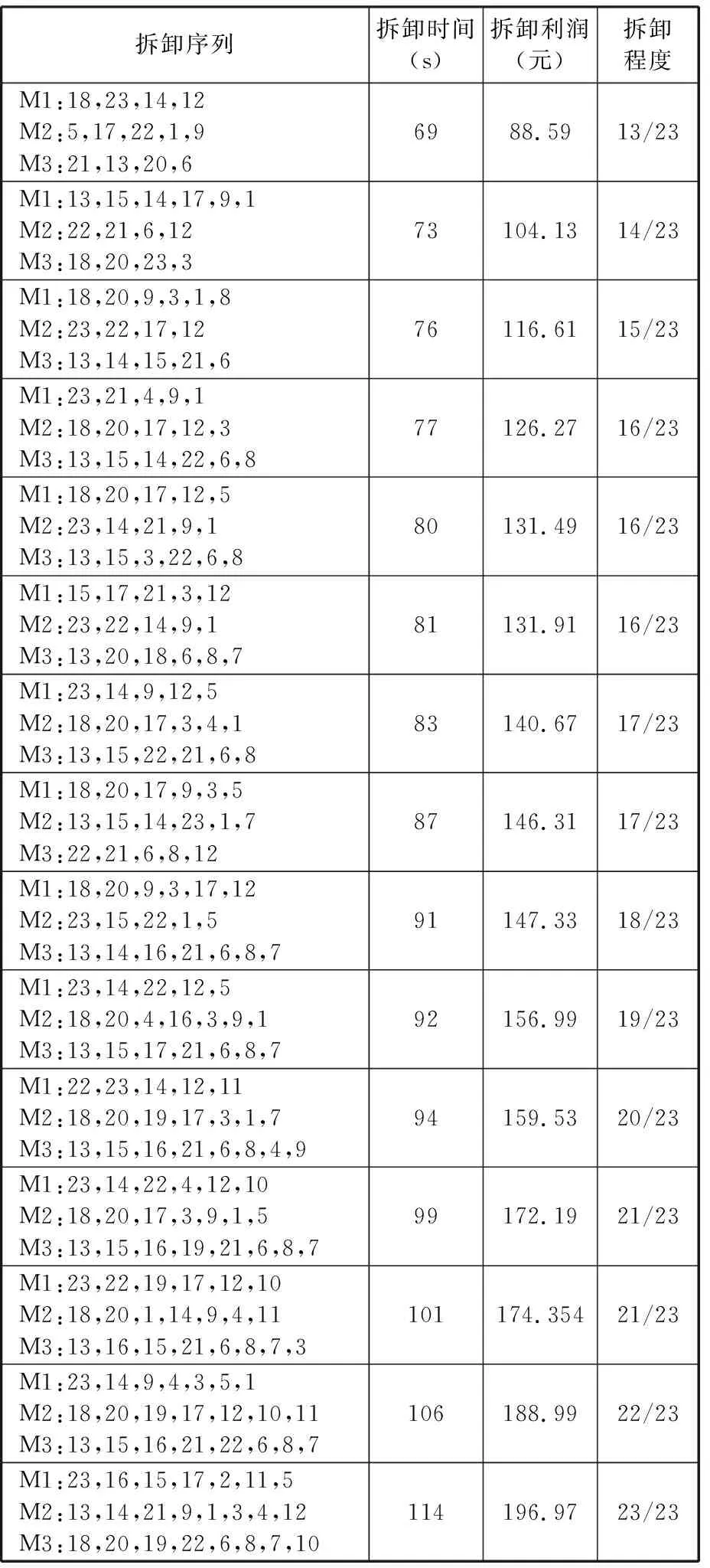
表6 案例一:不定拆卸程度选择性异步并行拆卸非支配解集
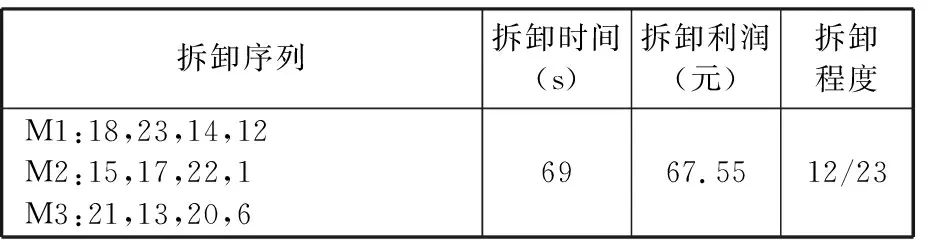
表7 案例一:定拆卸程度选择性异步并行拆卸最优解

(a)不定拆卸程度选择性异步并行拆卸非支配解集示例
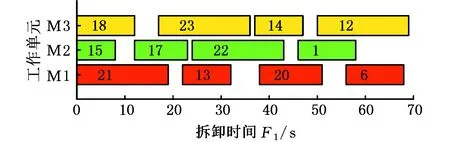
(b)定拆卸程度选择性异步并行拆卸最优解示例图13 案例一:Cd={1,6,12},并行度为3时最优解甘特图Fig.13 Case 1:Gantt chart of optimal solution whenCd={1,6,12}, degrees of parallelism is 3
3.2.2案例二
算法参数设置:种群大小Psize=200,迭代次数Gmax=1000,栖息地最大突变率Pmax=0.1,平均邻域大小K=12, 非支配解集无改善迭代次数上限Nmax=20。针对本文所提不定拆卸程度选择性异步并行拆卸问题,设目标件Cd={1,3,7,14,29},并行度为3,计算结果Pareto解集空间分布如图14所示,其中详细拆卸序列信息见表8。作为对比,设置同样的目标件、并行度,传统定拆卸程度下的选择性异步并行拆卸优化结果见表9。不定拆卸程度模式非支配解集表8中第一个解方案的拆卸甘特图见图15a,定拆卸程度模式最优解的拆卸甘特图见图15b。

图14 案例二:Pareto解集空间分布Fig.14 Case 2: spatial distribution of Pareto solution set
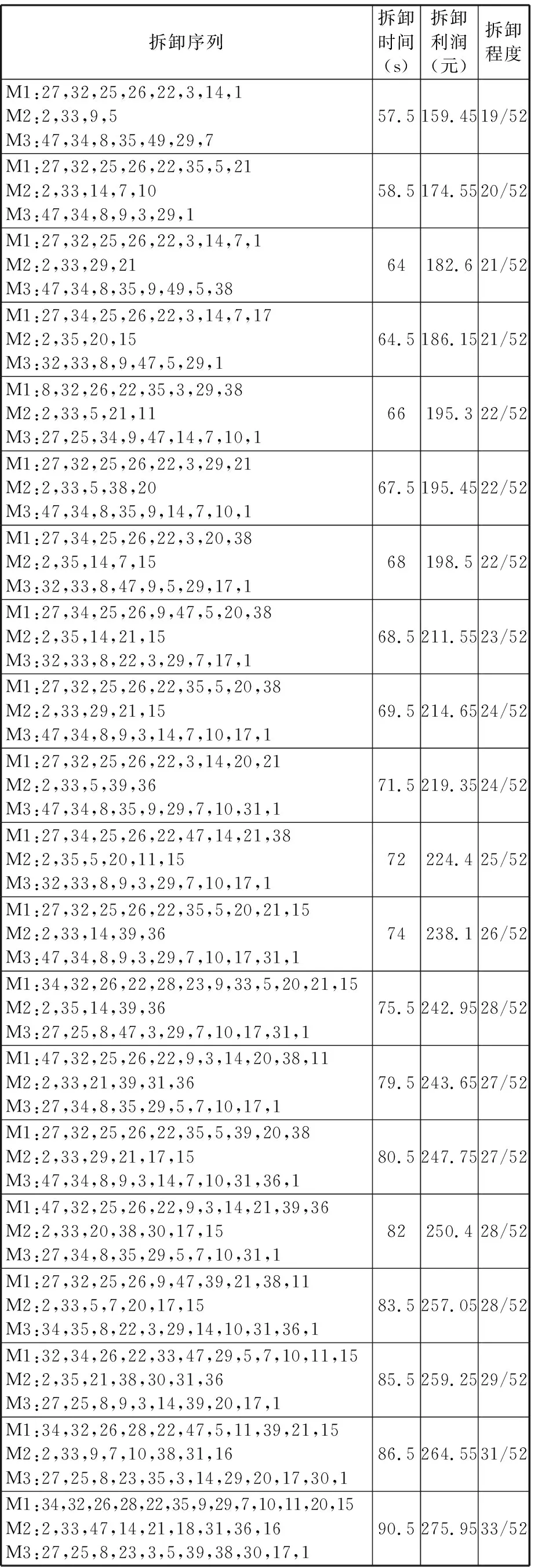
表8 案例二:不定拆卸程度选择性异步并行拆卸非支配解集

表9 案例二:定拆卸程度选择性异步并行拆卸最优解
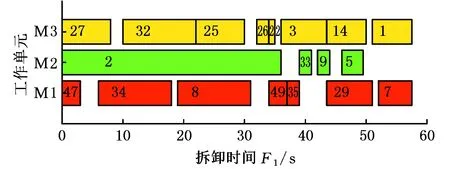
(a)不定拆卸程度选择性异步并行拆卸非支配解集示例

(b)定拆卸程度选择性异步并行拆卸最优解示例图15 案例二:Cd={1,3,7,14,29},并行度为3时最优解甘特图Fig.15 Case 2:Gantt chart of optimal solution whenCd={1,3,7,14,29}, degrees of parallelism is 3
3.3 实例对比结果分析
观察图13与图15可以发现,本文所提不定拆卸程度选择性异步并行拆卸能在相同的拆卸时间内充分利用由拆卸优先约束造成的等待时间,进一步拆卸了多个非最小拆卸集合中的零件,从而在相同的拆卸时间内获取了更多的利润。
观察两个试验案例的不定程度选择性异步并行拆卸解集展示表6与表8,与定程度选择性异步并行拆卸解集展示表7与表9,可以发现不定拆卸程度选择性异步并行拆卸为决策者提供了多种不同拆卸程度的决策方案,在实际应用中有较好的实际意义。
4 算法对比
为证明本文所提MRTBBO算法解决不定拆卸程度的选择性异步并行拆卸问题的优越性,将其与经典多目标优化算法:快速非支配排序遗传算法(NSGA-Ⅱ)、多目标粒子群优化算法(MOPSO)、多目标生物地理学优化算法(MOBBO)[18]、基于模糊Pareto支配的生物地理学优化算法(FPDCBBO)[19]、多目标扰动生物地理学优化算法(MDBBO)[20]进行对比试验。
采用多目标算法的综合度量指标反世代距离(inverted generational distance,IGD)、多样性度量指标间距(spacing,S)和准确性度量指标成功率(success ratio,SR)作为算法性能评价指标,IGD值越小代表算法的收敛性越好,分布越均匀,S值越小代表算法的多样性越好,SR值越大说明算法性能越好[21]。
所有算法种群规模均设为200,迭代1000次。各算法的参数设定如下:MRTBBO的最大变异率为0.1,平均邻域大小为20,非劣解无改善代数上限为30;NSGA-Ⅱ的交叉概率为0.9,变异率为0.1;MOPSO的最大惯性权重为1.2,最小惯性权重为0.6,个体因子为0.8,社会因子为0.8。MOBBO、FPDCBBO、MDBBO的最大变异率均为0.1。将各算法独立运行20次,取20次结果的平均值作为最终的测试结果,各性能指标结果见表10,案例一与案例二中一次运算的各算法求得的Pareto解集空间分布图分别见图16、图17。

表10 各算法性能指标测试结果
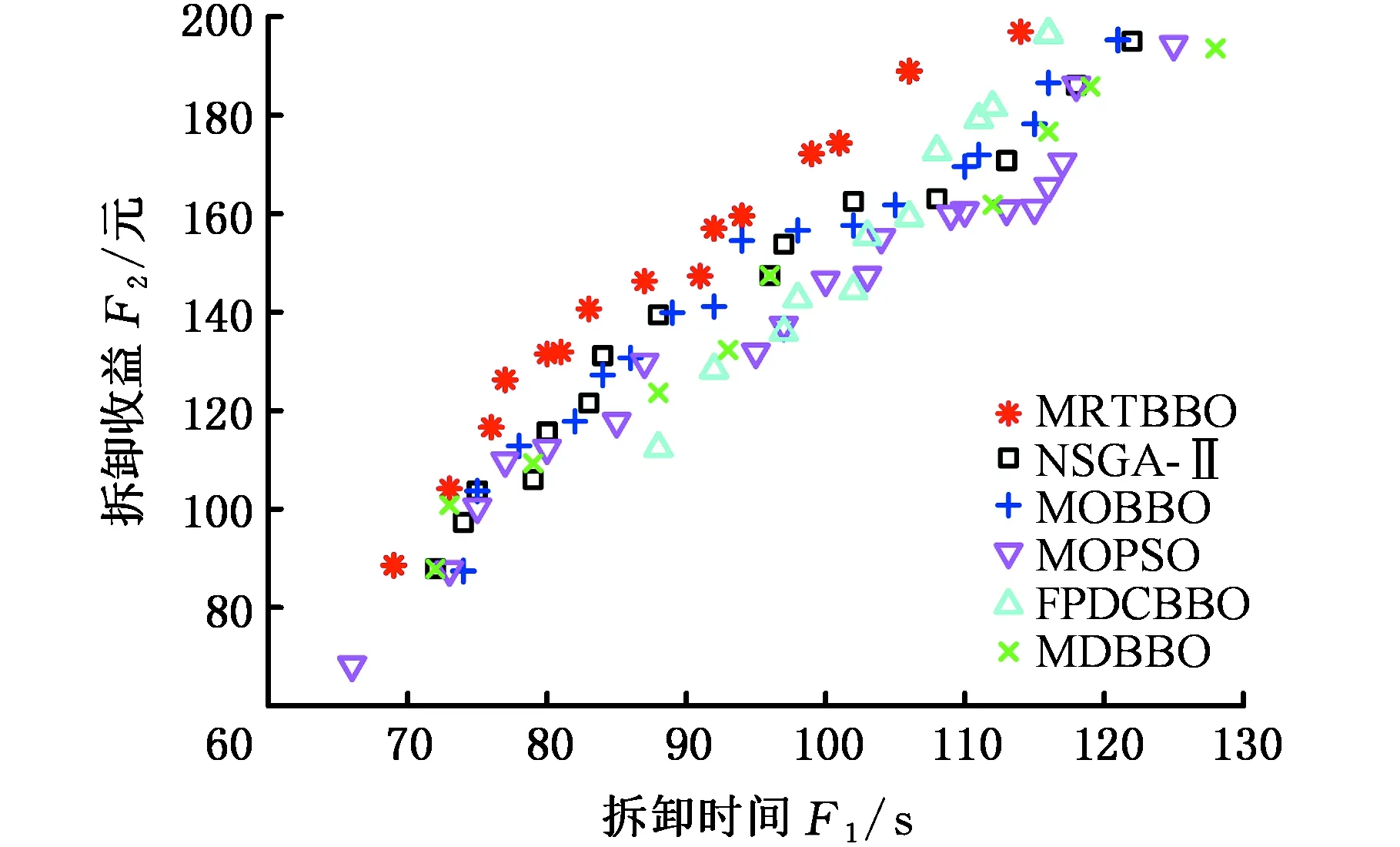
图16 案例一:各算法Pareto解集空间分布Fig.16 Case 1:spatial distribution of Pareto solutionset of each algorithm
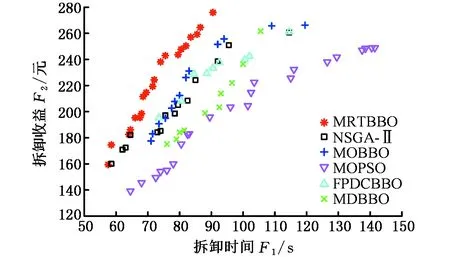
图17 案例二:各算法Pareto解集空间分布Fig.17 Case 2:spatial distribution of Pareto solutionset of each algorithm
观察表10对比结果与解空间分布图16及图17,MRTBBO算法性能指标在两个案例中均优于另5种算法,表明在解决不定程度的选择性异步并行拆卸问题上,MRTBBO可以在相同的测试条件下更接近真实Pareto前沿且解的多样性更好,算法性能更好。依据本文改进的生物地理学算法MRTBBO与未做改进的多目标生物地理学算法MOBBO的数据进行对比,结果表明本文采取的基于随机拓扑结构的迁移策略可以有效提高多目标BBO算法的搜索性能。
5 结论
为了提高废旧产品再生过程中的再生收益,本文研究了考虑不定拆卸程度的选择性拆卸问题,建立了以拆卸总时间最短和拆卸总收益最大为优化目标的考虑不定拆卸程度的选择性异步并行拆卸模型;针对该模型特点,提出了一种改进的生物地理学优化算法。设计了一种三层链表的编码解码方式来避免不可行拆卸序列的产生,提出了基于随机拓扑结构的迁移策略以提高算法的搜索性能;通过两种不同规模的试验案例验证了不定拆卸程度的选择性异步并行拆卸序列规划模型,能在考虑最小待拆件集合之外,充分利用由拆卸优先约束造成的等待时间,进而拆卸更多的零部件,并为决策者提供多个拆卸方案。最后通过对比算法试验验证了本文所提算法改进机制的合理性,以及解决不定拆卸程度的选择性异步并行拆卸问题的有效性。未来将进一步深入研究考虑废旧产品质量状态的拆卸序列规划模型与解决方法。
