基于NSST 和NLMF 的多聚焦图像融合*

吴 剑 ，吴晓红 ，何小海 ，李林怡 ，卿粼波

(1.四川大学 电子信息学院 图像信息研究所，四川 成都610065；2.中国民航局第二研究所，四川 成都610041)

0 引言

图像技术的不断发展以及现代光学成像设备的聚焦范围局限性，很难保证成像图像都位于聚焦区域。多聚焦图像融合技术将同一场景通过相同传感器得到的不同聚焦信息有效地整合在一起，形成一幅内容丰富、信息饱和的聚焦图像，可应用在遥感技术、医学图像和摄影等方面。

基于变换域的融合方法将源图像通过各种变换以得到多尺度、多方向的多幅子带图像；然后，通过各种融合规则对子带图像进行融合；再通过反变换得到最终融合图像。非下采样轮廓波变换(Non-Subsampled Contourlet Transform，NSCT)[1]的提出主要解决了融合图像的边缘及轮廓表现得不是很明显的问题。但是此变换忽视了空间一致性。通过NSCT[2-3]和脉冲耦合神经网络(Pulse Coupled Neural Network，PCNN)的有效结合，不仅解决了空间一致性问题，同时也实现了更好的视觉效果。由于非下采样剪切波变换(Non-Subsampled Shearlet Transform，NSST)[4]具有多方向、多尺度变换，平移不变等良好特性，也被用于图像融合。稀疏表示(Sparse Representations，SR)[5]、低秩表示(Low-Rank Representation，LRR)[6]最近几年也相继出现在图像融合领域，LRR 在带有噪声的图像融合中表现较为突出。基于卷积神经网络(Convolutional Neural Networks，CNN)的图像融合技术[7]等也被提出，并且达到了很好的视觉效果。

BUDADES A 等提出的非局部均值滤波(Non-Local Mean Filter，NLMF)算法[8]不仅能达到去除噪声的目的，还能在很大程度上保留图像的结构信息。

本文利用NSST 以及NLMF 的各自优势，提出了一种基于NSST 与NLMF 的多聚焦图像融合算法，有效提高了融合图像的视觉效果。

1 相关理论

1.1 非下采样Shearlet 变换

NSST 是对Shearlet 变换的改进，针对Shearlet 变换在下采样过程中不具备平移不变性的缺点而提出的。NSST 变换通过非下采样金字塔滤波器组(Non-Subsampled Pyramid Filter，NSPF)对源图像进行多尺度剖分，再利用基于改进的剪切波滤波器组(Shearlet Filter Box，SFB)进行多尺度局部化分解。分解原理如图1 所示，利用NSPF 对源图像进行K级分解后得到高频和低频子带系数，再利用SFB 对每一级的高频子带系数进行多方向局部化分解，最终可以得到K个高频子带图像和一个低频子带图像，且子带图像大小与源图像尺寸一致。

1.2 非局部均值滤波

NLMF 是对传统滤波的一种改进。该算法考虑到图像的自相似性，充分利用图像的冗余信息，较大程度地保留了图像的细节特征，与传统均值滤波不同之处在于：获得权值w的策略不同。其计算公式如下：

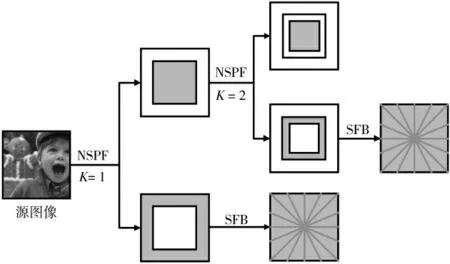
图1 NSST 分解原理图

式中，ui表示输入RGB 图像，i=1，2，3；B(p，r)表示中心像素点为p，大小为(2r+1)×(2r+1)的像素块。w为权重，计算公式如下：

这里采用指数函数对两个像素块之间的平方距离d2进行权值计算(本文采用递增指数函数，尽可能平滑边缘)，B(p，f)、B(q，f)分别表示中心像素为p、q，大小为(2f+1)×(2f+1)的像素块。

2 基于NSST 和NLMF 的融合算法

2.1 融合算法

输入源图像，经过NSST 变换得到低频子带图像以及一系列高频子带图像。针对低频子带图像，采用基于局部区域的改进拉普拉斯能量和以及NLMF 修正规则；针对高频子带图像,采用相位一致性(Phase Congruency，PC)以及空间频率和能量相关系数的融合规则。最后通过NSST 反变换得到最终融合图像。

2.2 低频子带系数融合规则

2.2.1 初始融合规则

2.2.2 NLMF 修正融合规则

2.3 高频子带系数融合规则

2.3.1 初始融合规则

高频子带图像中，纹理、边缘细节信息居多。本文针对高频子带系数，设计了一种基于相关系数的空间频率和能量相结合的加权融合规则(SF_Eng_Corr)：

2.3.2 相位一致性修正融合规则

由相关系数得到的初始高频融合权重忽视了高频子带系数本身的相关性，为此，本文采用相位一致性加以修正，其过程如下：

3 实验结果及分析

3.1 实验说明

为对本文提出算法的可行性进行有效验证，进行了一系列对比实验。实验中选取3 组不同聚焦图像进行融合实验，并与现有的5 种常见算法进行比较，分别为文献[10](GFF 方法)、文献[2](NSCT 方法)、文献[5](ASR 方法)、文献[7](CNN 方法)以及文献[11](GFDF 方法)。所用对比图片均已配准；对融合结果分别在主观视觉和客观评价指标上进行了分析。

3.2 主观评价

图2～图4 展示了不同融合算法对Clock、Disk、Pepsi 三对不同聚焦图片的融合结果。在Clock 的实验结果中，相对于源图像2，NSCT、ASR、CNN 方法在聚焦边缘(如图中框中所示)存在边缘模糊、缺失现象；同时，ASR 方法得出的融合图像在图像清晰度方面有所不足，细节部分有所丢失。而GFF、GFDF以及本文方法在图像清晰度、边缘部分都有很好的表现,融合效果较好。

在Disk 的实验结果中，ASR 以及CNN 方法在聚焦边缘(中间小方框中)存在细节缺失、不平滑现象；同时，在书架上白色书籍边缘(左边方框中)，NSCT、ASR方法存在白色光晕现象。GFF、GFDF 以及本文算法并未出现上述现象，同时图像细节保留很好，清晰度较高。

在Pepsi 的实验结果中，NSCT 和ASR 方法在图中英文单词处(右上方框中)有轻微的模糊现象，清晰度不高；同时，相对于源图像2，GFF、NSCT 以及ASR 方法在图中桌面倒影处(偏右下长方形小框)也存在些许模糊。从主观上看，本文算法不管是在聚焦边缘、细节保留还是在图像清晰上，都有一定的提高,融合效果相对较好。

图2 Clock 实验结果

图3 Disk 实验结果

3.3 客观评价

为对本文算法的有效性做进一步的验证，选取了5 个评价指标对融合图像进行定量评估，分别为互信息(MI)[12]、标准差(STD)、视觉信息保真度(VIFF)[13]、结构相似性(SSIM)[14]、结构互信息(QFMI)[15]。其中，融合图像包含的信息量越多，MI、QFMI越大。STD 反映图像对比度，越大则对比度越高。VIFF 反映人眼视觉效果，其越大，视觉效果越好。SSIM 反映的是融合图像与参考图像之间的相似度，其值越接近1，融合效果越好。

图4 Pepsi 实验结果

表1 列出了评价指标对比结果，从表中可以看出，对于融合图像Clock 和Disk 的对比实验结果，本文算法的MI、SSIM、QFMI均高于其他几种算法，特别是SSIM 接近于1。可见,本文算法得出的融合图像中所包含源图像的聚焦信息与其余算法相比，有较大的提升。对于融合图像Clock 和Pepsi 的实验结果，MI、VIFF 均高于其余算法，说明在保留较多源图像的聚焦信息的同时，融合图像的视觉效果也较优于其余算法。在图像Clock 的融合结果中，MI、STD、VIFF、SSIM、QFMI都优于其余算法，说明本文算法在信息丰富度、对比度、人眼视觉效果上都有较好的表现。三组实验中，本文算法的MI、STD、VIFF、SSIM、QFMI均高于NSCT、ASR 方法；并且，相对于当前对比的深度学习算法，本文算法在MI、VIFF、SSIM、QFMI指标上均有一定的优势。

结合主观评价和客观评价，本文算法的融合效果较其他几种算法都有较好的优势，特别在融合图像的信息丰富度、对比度上，有较大的提高。同时，本文算法也提高了融合图像的人眼视觉效果。

表1 客观评价结果

4 结论

多聚焦图像融合弥补了传统数字成像设备不能聚焦全部场景信息的不足。本文运用非局部均值滤波、改进拉普拉斯能量和以及相位一致性等理论，提出了一种基于NSST 和NLMF 的多聚焦图像融合算法。根据仿真结果，得到以下结论：

(1)本文算法不仅有效地保留了源图像的轮廓、纹理等细节信息，同时，在图像的聚焦边缘区域，也有良好的视觉效果。

(2)相比于其他五种算法，本文算法得出的融合图像的对比清晰度有一定的提升，在互信息量以及结构相似度上提升明显，融合效果较理想。

未来工作考虑将更多的图像色彩信息与纹理细节有效地结合起来，提高融合效果的同时，使得融合图像的色彩饱满度得到提升；同时，对于带噪图像的融合方法也是今后考虑的方向。