一种基于SVM的主动多分类方法

郭金玲

（山西大学商务学院 信息学院，山西 太原 030031）

0 引言

支撑向量机是一种以结构风险最小化原理为准则的有效的机器学习方法，在数据分类、预测等研究领域应用较为广泛[1-5]。近年来，伴随大数据技术的发展，针对大规模数据的多分类模型的建立成为数据挖掘技术的研究热点[6-10]。许多学者在对SVM技术进行深入研究后，提出了多种基于SVM的多分类模型，如一对一、一对多、决策树、有向无环图等多分类算法[11-15]。

“一对一”多分类算法的主要思路是在每两类样本之间构造一个二分类器，如果有k类样本，二分类器的个数将达到，该方法构造的分类器个数过多，存在分类器个数过多导致不可分区域出现的弊端。“一对多”多分类算法的主要思路是锁定某一类数据，其余类别的数据都归为另一类，在两者之间构造一个分类器，如果有k类样本，二分类器的个数为k，该方法构造的二分类器个数较少，但是在训练分类器的过程中，需要所有的训练样本参与计算，计算量过大，训练时间过长。“决策树”多分类算法通过计算数据类别的信息熵增益，首先分离出类别属性最易区分的数据，以此类推，从而构造出多分类模型，由于每次分类都需要计算信息熵增益，导致该模型的计算量过大。“有向无环图”算法结合图论和“一对一”算法的解决思路，将若干个二分类器组合得到多分类器，其缺点是分类效果过度依赖于有向无环图中有向节点的排列顺序，算法过于冗余。总体来看，目前提出的比较成熟的多分类模型可以解决数据挖掘中的多分类问题，但存在计算量大、训练时间长、泛化性较低等问题[16-19]。

针对传统的多分类模型构造过程存在的上述问题，本文提出一种基于SVM的主动多分类方法，该方法基于“一对多”SVM多分类算法思路，通过引入就绪分类器和阻塞分类器的概念，将主动学习的策略用于SVM多分类器的构造过程，不再是所有样本参与训练，按照一定的规则，每次选取最有价值的样本训练分类器，实现高效、准确构造分类器的过程，从而可降低计算复杂度，有效提高多分类器的泛化性。

1 基于SVM的主动多分类方法

本文采用“一对多”的思想构造SVM多分类模型，假设训练数据集包含l个样本、c个类别，表示为其中，xi∈Rd，Y为类别标签且yi∈{1，2，···，c}，通过“一对多”多分类方法得到的多分类器集合包含c个二类分类器，表示为F={f1，f2，···，fc}。

1.1 就绪分类器与阻塞分类器

假设第i类样本与其他类样本之间构造的分类器表示为fi，训练样本集X中的任意样本xj(j=1，···，l）与分类器fi之间的距离表示为|fi(xj)|。

就绪分类器fi是指对于训练数据集存在样本xj位于fi的分类间隔内，即|fi(xj)|＜1成立；阻塞分类器fi是指训练数据集中所有的样本位于fi的分类间隔外，即对于任意样本xj，均为|fi(xj)|≥1。

根据SVM分类器构造原理分析，可以得到以下结论：

（1）如果分类器fi处于阻塞状态，即所有训练样本位于fi的分类间隔外，则这个超平面进行硬间隔的主动学习没有意义。

（2）如果分类器fi处于就绪状态，采用SVM分类算法进行训练，一定可以获得更新的分类器集合。

（3）如果存在多个就绪状态的分类器f1、f2、…，即存在多个|fi(xj)|＜1，选择和分类超平面距离最小的|fi(xj)|min对应的样本xj，xj将被选为最有价值的样本投入本轮主动分类模型的训练中。

以上结论应用于基于SVM的主动多分类模型构造过程中，每次训练只选取处于就绪状态的分类器，可有效减少每轮需要训练的分类器数目。另外，结论（3）为如何选取最有价值样本提供了选取策略，保证了主动多分类器高效、准确地进行更新和构造。

1.2 基于SVM的主动多分类算法

基于SVM的主动多分类算法首先采用k-均值聚类方法，以各个类的中心样本训练得到初始分类器集合，并划分为就绪分类器集合与阻塞分类器集合；然后选择最有价值的样本对就绪分类器进行训练；训练过程中，由于训练样本的不断加入，就绪分类器集合与阻塞分类器集合不断更新，该过程迭代进行，直到所有分类器停止更新。该主动多分类方法一方面减少了需要训练的分类器的数量；另一方面可有效选取最有价值的样本，从分类器和样本数量两方面进行了优化，降低了分类模型构造的复杂度，提高了分类器的效率。

假设测试数据集包含t个样本，表示为基于SVM的主动多分类算法主要包含以下步骤：

Step 1： 对训练数据集采用k-均值聚类方法，以各个类的中心样本训练得到初始分类器集合F0。

Step 2： 根据就绪分类器与阻塞分类器的划分规则，将初始分类器集合F0分为就绪分类器集合F0-m与阻塞分类器集合F0-n。

Step 3： 选择就绪分类器集合F0-m中距离每个分类器间隔超平面最近的样本，并计算出各个距离值|fi(xj)|，选择|fi(xj)|min对应的样本xj参与本轮分类模型的训练。

Step 4： 动态更新就绪分类器集合F0-m与阻塞分类器集合F0-n，采用测试数据集TE测试分类器精度。

Step 5： 循环执行步骤3-步骤4，直到分类器集合F停止更新，基于SVM的主动多分类模型构造完成，算法结束。

K-均值聚类方法的初始化方式包括三种：（1）将训练样本随机划分为k个部分；（2）随机选择与训练样本一致的样本空间中的三个点作为初始聚类中心；（3）从训练样本中随机选择k个样本作为初始聚类中心。本文采用第三种方式进行选择。

虽然初始聚类中心的选取对聚类结果的影响不大，但对于聚类的收敛速度有较大影响。本文首先从训练样本中随机选择一个样本点作为初始聚类中心的第一个样本，然后选择距离该样本点最远的样本作为第二个样本点，之后再选择聚类这两个样本平均距离最远的样本作为第三个样本点，如此循环往复，直到选择的样本点数达到k个，由于采用该种方法选择的聚类中心距离相差较大，而K均值聚类的目标就是将相似度较大的样本聚为一类，把不相似的样本通过聚类过程分离，因此，此种初始化方式可以使得算法快速收敛。

本文提出的主动多分类方法首先采用K-均值聚类，其复杂度为O(kdl)，其中l为样本规模，k为聚类个数，d为迭代次数，且k＜＜l和d＜＜l成立。在此基础上，采用聚类中心得到初始分类器，并反复选择就绪分类器中距离分类面最近的样本加入训练，并进行超平面的更新，直到算法收敛。假设分类器更新次数为n，结合SVM训练的时间复杂度可知，更新过程的时间复杂度为O(k3n)，由于在分类器更新过程中，选择距离就绪分类器最近的样本进行超平面更新，可使得超平面快速收敛，因此分类器更新次数为n很小。反之，如果直接用标准SVM进行主动学习的话，一方面需要的专家标记代价很大，因为所有参与训练的样本都需要进行专家标记；另一方面，其时间复杂度为O(l3)，由于n＜＜l，因此本文提出的基于SVM的主动多分类方法具有较低的时间复杂度，可有效提高具有少量标记的弱监督多分类问题的学习效率。

2 实验结果与分析

为了测试基于SVM的主动多分类算法的性能，验证其有效性，基于UCI标准数据集，采用文中方法和一对一多分类方法、一对多多分类方法、决策树多分类方法、有向无环图多分类方法四种多分类方法进行了实验对比。实验采用SVM作为基准分类器，核函数选择高斯核，核函数参数σ取1.0。

2.1 实验数据集

实验采用的数据集包括UCI数据库中的Balance_scale、Glass、Iris等7个数据集，这些数据集均为多类别数据集，且包括训练集和测试集两部分，数据集的基本信息如表1所示。

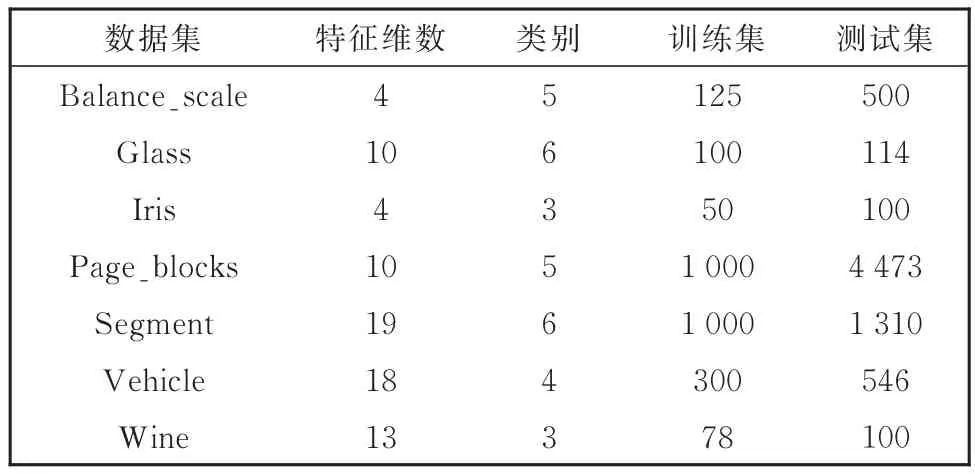
表1 实验数据集信息表Table 1 Datasets for the experiments

为了避免特征分量量纲不同对分类实验造成的影响，首先对数据集进行归一化处理[20]，计算过程如下：

2.2 测试结果与分析

采用文中方法和一对一、一对多、决策树、有向无环图四种多分类方法，分别对UCI数据库中7个数据集进行了分类对比实验，表2记录了不同方法在各个数据集上进行实验的分类精度，其中，带下划线的值代表了文中方法的分类精度高于其余方法的情况，从表2可以看出，文中方法在Balance_scale、Glass、Wine、Vehicle、Iris 5 个实验数据集上的测试精度都高于其他方法，在Page_block、Segment两个数据集上和其余方法的测试精度比较接近，区分度不大。文中提出的主动多分类方法主要通过欧式距离的计算来获取最佳训练样本，考虑到样本分布的复杂性，Page_block、Segment两个数据集采用文中方法进行分类，没有明显提高分类精度。

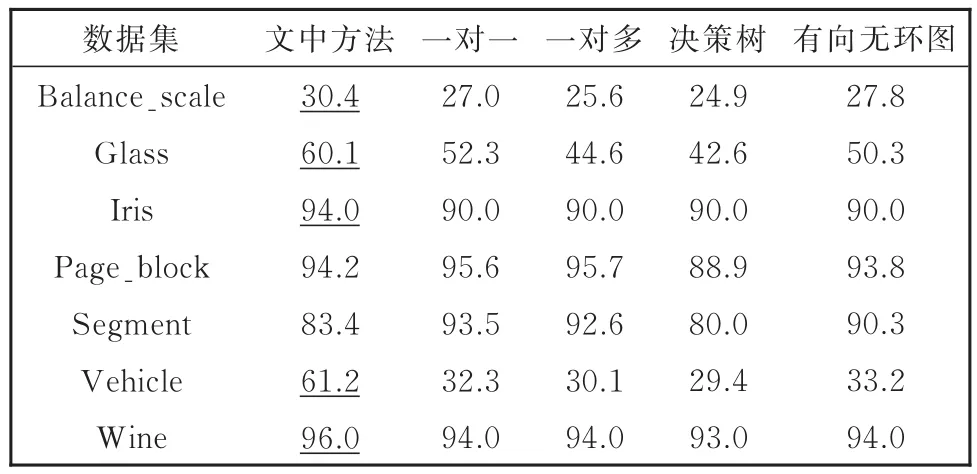
表2 不同方法的分类结果比较（%）Table 2 Comparison among testing results（%）

实验时间是衡量分类算法优劣的一个重要指标，表3给出了不同方法在各个数据集上的训练时间对比。从表3可以看出，在不同数据集的分类实验过程中，文中提出的方法较其余方法实验时间较短，有效提高了分类器训练的速度。

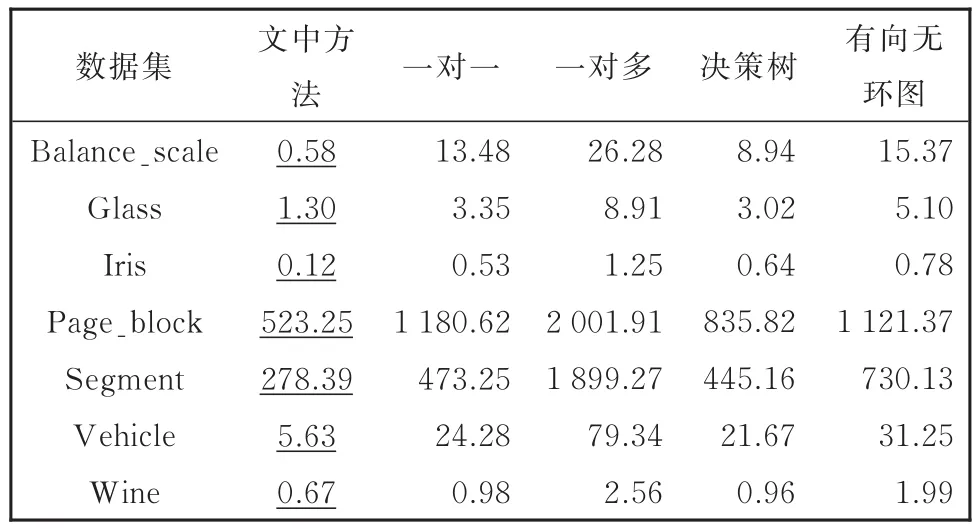
表3 不同方法的训练时间对比（s）Table 3 Comparison among training time（s）

综合以上实验结果，结合表2和表3记录的实验数据分析，本文提出的基于SVM的主动多分类方法，从分类器数量和训练样本两方面进行优化，通过动态控制分类器的有效参与，选取最有价值的样本参与训练，从而提高了分类器的精度，降低了训练的时间，提高了学习效率。

3 结论

针对传统的多分类模型构造过程存在的计算量大、效率低等问题，本文提出一种基于SVM的主动多分类方法，该方法基于“一对多”SVM多分类算法思路，通过引入就绪分类器和阻塞分类器的概念，将主动学习的策略用于SVM多分类器的构造过程，从分类器数量和训练样本两方面进行优化，降低了计算复杂度，有效提高了多分类器的泛化性。考虑到大数据领域数据集分布的多样性、复杂性，如何结合不同数据集的特征选取最有价值的训练样本，并设计对应的算法，值得进一步的探讨与研究。