基于动态分配邻域策略的分解多目标进化算法

王丽萍，沈 笑，吴 洋，俞 维

(1.浙江工业大学 计算机科学与技术学院，浙江 杭州 310023；2.浙江工业大学 信息智能与决策优化研究所，浙江 杭州 310023；3.浙江工业大学 管理学院，浙江 杭州 310023)

在实际工程应用领域，需要优化的目标个数往往不止一个。如在桥梁设计工程中，通常期望在最大限度提高工程安全性的同时尽可能降低作业成本。在物流配送中，通常期望在提高工作效率的同时实现成本最低，并且使服务质量达到最优。因此，这类具有两个或两个以上相互冲突目标的优化问题被称为多目标优化问题(MOPs)[1]。目前，解决这类问题的有效方法是在多个目标之间找到一组折中解，使得各个目标尽可能地逼近各自的最优解，也称为帕累托最优解(Pareto-optimal，P-O)[2]。多目标进化算法(Multi-objective evolutionary algorithms，MOEAs)通过模拟种群进化过程，在迭代过程中淘汰劣解，保留P-O，在近20 年的演化计算中被证实能有效求解MOPs[3-4]。

多目标进化算法按进化机制可以分为基于支配关系的MOEAs、基于指标的MOEAs和基于分解的MOEAs。其中，基于分解的MOEAs具有强搜索能力、较低的算法复杂度和局部搜索的高兼容性，备受国内外学者关注。基于分解的多目标进化算法(MOEA based on decomposition，MOEA/D)由Zhang等[2]提出，其主要思想是通过聚合函数将MOPs分解为多个单目标子问题协同优化，对于解决高维MOPs效果良好，目前已经成为一类主流方法[5]。为进一步提高算法性能，基于分解的改进算法相继被提出。Tan等[6]提出了一种MOEA/D的新版本，称为MOEA/D+统一设计：针对基于分解的多目标进化算法的新版本，利用混合物实验均匀设计(UDEM)生成权重向量，该方法所产生的权重向量比单纯形网格设计方法所生成的权重向量更均匀；Cheng等[7]提出了基于参考向量的多目标进化算法，该算法提出了一种新的分解方法——角度惩罚距离(Angle penalized distance，APD)，该方法在搜索阶段前期注重收敛性，后期注重多样性，适用于具有不同目标数量的不同问题；Qi等[8]提出基于自适应权重调整的MOEA/D，通过分析切比雪夫分解法下的权重向量与最优解的几何关系，提出了一种新的权重向量初始化方法和自适应权重向量调整策略，周期性地调整权重向量以得到更均匀分布的解；Li等[9]提出基于差分进化的MOEA/D，利用DE算子和多项式突变为每个子问题生成一个新解，以提高处理复杂Pareto前沿的能力；Wang等[10]提出了一种算法全局替换的分解多目标进化算法，证明了替换邻域对不同问题通常是不同的；Chen等[11]提出一种基于稳态匹配选择的MOEA/D来协调MOEA/D中的解个体和子问题的互相匹配过程，为每个子问题选择一个最佳匹配个体，从而平衡算法的收敛性和多样性；Yuan等[12]提出基于距离更新策略的MOEA/D，该算法提出替换邻域的概念，通过计算新解到子问题的垂直距离来确定新解的邻域范围，并选取邻域内合适的解进行替换，该算法对处理高维目标优化问题性能良好；Zhao等[13]提出了基于集成邻域大小的MOEA/D，强调邻域大小对MOEA/D性能的影响，实验证明不同邻域大小适用于不同的MOPs；Wang等[14]在MOEA/D-GR[10]的基础上进行了拓展，提出线性、指数和S形指数3种策略自适应调整替换邻域的大小，形成一种基于自适应替换策略的稳态算法。

邻域的设置对于分解算法性能至关重要，父代个体的选择和子代个体的替换都取决于邻域的构成和规模。在进化过程中，以上分解算法通常采用固定邻域的方式，为每个个体分配相同的邻域规模。但显然每个个体的搜索能力不同，所需要的邻域规模也不等。基于此，笔者提出了一种基于动态分配邻域策略的多目标进化算法(MOEA/D-SD)。该算法通过衡量新解相对于旧解在收敛方向和多样性角度上的综合改进量来评估个体的进化状态，且根据个体进化状态动态调节邻域大小，对进化状态相对较好的个体分配更多的邻域以带动周围更多个体协同进化，从而合理利用有限的计算资源及提高算法的运行效率。

1 背景知识

多目标优化问题(MOP)[2]可以表示为

minF(x)=(f1(x),…,fm(x))T

(1)

subject tox∈Ω

式中：F(x)为具有m个目标的优化问题；Ω为决策空间；x=(x1,x2,…,xn)为决策空间的一个n维决策向量。

1.1 分解方法

MOEA/D通过聚合函数将一个MOP式(1)分解为若干个标量优化子问题，并同时对其进行优化。其中聚合函数主要有加权和聚合法(Weighted sum，WS)、惩罚边界交叉聚合法(Penaty boundary intersection，PBI)和切比雪夫聚合法(Tchebycheff，Tch)。加权和聚合法适用于凸的帕累托前沿(Pareto fronts，PFs)(最小化问题)，对于非凸的PFs，它不能近似整个PF；惩罚边界交叉聚合法中有一个惩罚参数θ，优化效果受惩罚参数θ的影响较大；切比雪夫聚合法对凸和非凸的问题具有相同的优化效果，且优化过程无需进行参数调整。

综上，笔者采用了MOEA/D中的切比雪夫聚合法，将理想Pareto前沿的MOP分解成N个标量优化子问题，即

(2)

(3)

1.2 权重生成方法

在MOEA/D框架中，权重向量生成方法的选择是影响算法性能的重要因素之一[5]。当决策者不提供任何偏好信息的时候，生成相对均匀分布的权重向量要比生成不均匀分布的权重向量所求得的解集，更能均匀地分布在PF上。在MOEA/D-SD算法中，为了所得解集能均匀分布在PF上，沿用了原始MOEA/D算法中的单格子点法来生成相对均匀分布的权重向量(λ1,…,λN)，即

(4)

(5)

1.3 邻 域

在MOEA/D中，子问题利用相邻的子问题信息进行优化，如第i个子问题的邻域是由绑定的权重向量λi之间的欧几里德距离求离的最近的T个权重向量在λ1,λ2,…,λN中，通过邻域关系选择父代解，繁殖后代并产生新解，比较后用新解替代原始解，使得子问题朝着有利的方向进化。

2 问题描述及算法

2.1 问题描述

邻域贯穿整个算法中的两个重要环节：选择和替换。在MOEA/D算法中，子代个体的产生受其父代邻域个体的影响，邻域大小对算法有很大的影响。在原始MOEA/D中，更新过程中有些子问题相对于前一代的进化程度较高，有些则发生退化，但是每个子问题邻域仍设置为固定大小，在浪费计算资源的同时所得解分布也不均匀。

在更新过程中，要想有效地利用计算资源，提高算法性能，为不同子问题分配合适的邻域尤为重要。若为子问题分配邻域过大，在浪费资源的同时还会导致所得解偏离Pareto前沿；若为子问题分配邻域过小，则会使解陷入局部最优，同时无法保证解的多样性。因此，本研究根据不同子问题的进化程度为其选择合适的邻域规模T，以平衡种群的多样性和收敛性。

笔者以DTLZ[15]系列测试函数中的DTLZ1测试函数为例，通过二维图像分析邻域对MOEA/D算法性能的影响，其中种群规模为100。图1为当邻域T分别设置为10，15，20，25，30，35时，MOEA/D中同一子问题的解迭代70 次后的变化图，图中分别选择第1，31，51，71，91 个子问题。图1中不同的形状代表算法设置的邻域不同，不同深浅代表不同子问题上的解，图1中对于第1 个子问题和第21 个子问题，当邻域T=15，20时，所得解的多样性最优，其中，第1 个子问题中，当邻域T=20的收敛性比邻域T=15的好，而第21 个子问题刚好相反；在第51 个子问题中，当邻域T=15，20，25时，所得解为最优；在第81 个子问题中，当邻域T=30时，所得解为最优；在第91 个子问题中，当邻域T=20时，所得解为最优。另外，当邻域T=10时，种群难以逼近PF前沿；当邻域T=35时，种群发生了退化的现象。根据以上分析可知：种群在更新过程中，为不同子问题选择合适的邻域尤为重要。

图1 邻域改变时的性能变化图Fig.1 Performance change diagram when the solution changes

2.2 基于个体的进化状态动态分配邻域

选择邻域过小会导致种群陷入局部最优，不利于算法的多样性；若邻域过大会导致种群退化，解偏离PF前沿。为了克服固定邻域的缺陷，为每个子问题寻找合适的邻域并提高算法的性能，笔者提出了一种基于个体的进化状态动态分配邻域算法。算法1为MOEA/D-SD的主框架，算法2为根据个体进化状态动态分配邻域策略。

算法1MOEA/D-SD主框架

输入多目标问题式(1)；种群规模N；均匀分布的N个权重向量H：λ1,λ2,…,λN；邻域T规模Tmax=30，Tmin=15；Ui=1

输出x1,x2,…,xN，f1(x)，f2(x),…,fi(x)…

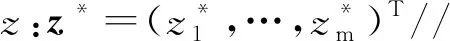
步骤1For gen=1 to max gen, do

步骤2If gen=1 to 50，do

步骤3T=(Tmax-(Tmax-Tmin)/2)

步骤4Else

步骤5Calculate the neighborhood size of all subproblems according to algorithm 2 //当代数大于50代时，通过算法2获得每个子问题的邻域规模

步骤6End if

步骤7Fori=1 toN，do

步骤8If rand()<δ

步骤9thenB=B(i) //从B(i)中随机选取xl和xk

步骤10Else

步骤11E=rand[1,N]//从整个种群中进行随机选取

步骤12End if

步骤13y←GeneticOperator(xl,xk) //进行交叉变异产生新解

步骤14UpdateIdealPoint(y;z*) //更新参考点

步骤15UpdateNeigh(y;z*;W;B(i);P) //更新解

步骤16End For

步骤17End For

在MOEA/D-SD主框架算法1中体现的本文贡献在于根据个体进化状态进行动态分配邻域，具体如图2所示。图2显示了两种测量方式：角度和距离，其中di和θi的计算公式分别为

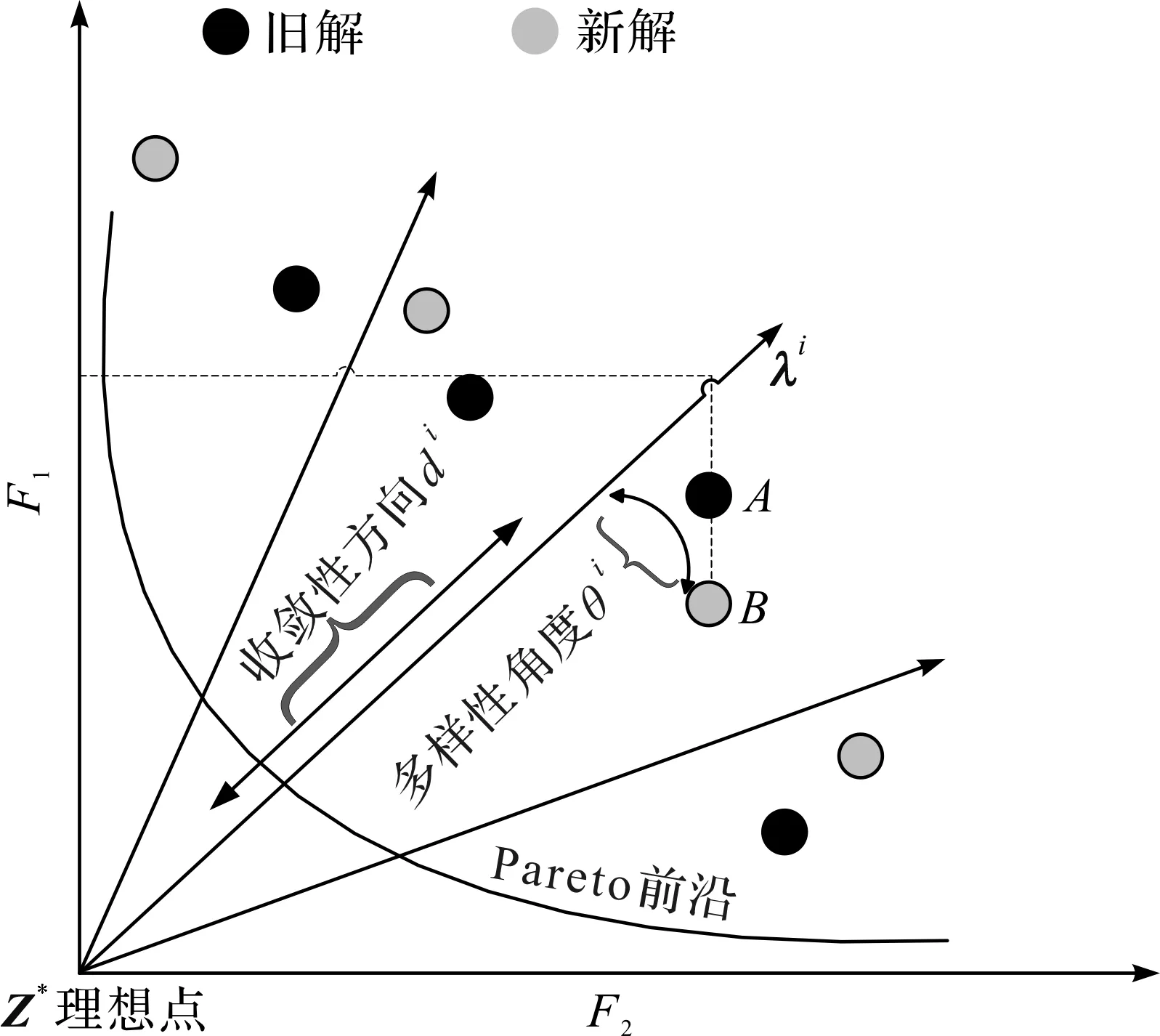
图2 个体进化状态动态分配邻域策略Fig.2 Individual evolutionary state dynamic allocation of neighborhood strategy

(6)

(7)

式(6)中di为y和z*之间的距离，式(7)中θi为y与λi之间的角度。其中：xi为第i个子问题；λi为第i个权重向量；z*为理想点即参考点。

笔者算法根据个体进化状态动态分配邻域策略具体步骤详见算法2。

算法2个体进化状态动态分配邻域策略

输入最大邻域值Tmax=30，最小邻域值Tmin=15；生成N个均匀分布的权重向量；Ui=1

输出T={T1,T2,…,TN}

步骤1Fori=1,…,N，do

步骤2计算Ui=((1-gen/max gen)·Δdi+(gen/max gen)·Δcosθi)·Ui，式中Δdi=diold-dinew，Δcosθi=1/(1/cosθiold-1/cosθinew) //计算个体的相对改进量

步骤3End For

式中，Ta=Tmin+(Tmax-Tmin)·((U)/max(U))//根据个体更新状态动态分配邻域

步骤5T=ceil(Ti)//邻域取整

笔者提出的个体进化状态动态分配邻域策略能更好地平衡算法的多样性和收敛性，并更合理地分配子问题的邻域。如图2所示，新解为子问题的当前解，旧解为子问题的先前解，根据di(收敛性方向)和θi(多样性角度)来衡量旧解与新解之间的综合相对改进量，并以此判定个体进化状态，根据个体的进化状态动态分配邻域，向PF进化变化大时，子问题能够更好地进化，将会分配更多的邻域使子问题得到更好的进化；向PF进化变化较小时，子问题陷入停滞，不应该分配更多的邻域以免浪费计算资源；远离PF进化时，子问题应该要分配更多的邻域，使个体得到进化，以免个体陷入局部最优。

3 仿真实验及结果分析

3.1 参数设置

为了减少随机因素对算法性能的影响，在每个测试函数上均运行20 次，取平均值和标准差作为最终的对比测试数据，选用二维ZDT系列[16]测试函数和三维DTLZ系列[15]测试函数对原始的MOEA/D[2]，MOEA/D-GR[10]和MOEA/D-SD进行算法性能对比，均使用Tchebyceff的聚合函数分解法、多项式变异算子以及单格子点法生成权重向量。其中，Tmin=15，Tmax=30仅在MOEA/D-SD中使用，T=20的邻域在MOEA/D、MOEA/D-GR中使用，其他参数设置均保持一致。在二维测试函数中，H=99，N=100；在三维测试函数中，H=13，N=105。在二维ZDT系列测试函数中种群最大进化代数为300，在三维DTLZ系列测试函数中DTLZ1和DTLZ3，DTLZ5和DTLZ6的种群进化代数为1 000；DTLZ2和DTLZ4最大进化代数为500。

3.2 性能评价指标

为了能够具体评价算法的性能，笔者使用以下3个指标作为评价准则：1) 世代距离评价指标(Generational distance，GD)[17]用来衡量算法的收敛性，指标值越小，代表算法的收敛性能越好；2) 反世代距离评价指标(Inverted generational distance，IGD)[18]是一个综合性能的指标，能够综合评价算法的收敛性能和多样性能，指标值越小，代表算法的综合性能越好；3) 超体积指标(Hyper volume，HV)[19]是一种综合性指标，能够同时衡量算法的多样性和收敛性，指标值越大，代表算法性能越好。

3.2.1 在ZDT系列测试函数上的算法性能对比

为衡量算法的收敛性和综合性，笔者在ZDT系列测试函数上运行20 次，求取GD指标和IGD指标的平均值和标准差作为最终数据对比值，并分别与MOEA/D和MOEA/D-GR算法进行对比。

表1中标黑数值表示对比算法中的各项最优数值。从表1可以看出：在ZDT系列测试函数中MOEA/D-SD算法的GD指标平均值和标准差均明显优于MOEA/D和MOEA/D-GR算法；同时，在IGD指标方面，除ZDT6测试函数，MOEA/D-SD算法均优于其他对比算法。由此可以看出：根据个体进化状态动态分配邻域对算法的资源能够进行有效分配，明显提高了算法的收敛性，且提升了算法的整体性能。

表1 3 种算法在ZDT测试函数上的指标对比Table 1 Index comparison of three algorithms in ZDT test function

为了直观地反映MOEA/D-SD算法性能的提高，运用算法运行20 次中IGD最小值数据绘制出MOEA/D和MOEA/D-SD在ZDT系列测试函数上的Pareto前沿和真实Pareto前沿对比图，以不同形状绘制以示区分：实心圆为MOEA/D-SD算法求得的Pareto最优解，空心圆为MOEA/D求得的Pareto最优解，十字形状为真实的Pareto前沿，每幅图中所附的小图是部分前沿区域的放大图。从图3可以看出：MOAE/D-SD算法求得的解集要比原始的MOEA/D算法求得的解集要更接近Pareto真实前沿，其中MOEA/D-SD在ZDT4中求得的解集很大程度接近了Pareto真实前沿，MOEA/D离真实前沿较远，证明了改进算法使算法性能得到了明显提高。

图3 3 种算法在ZDT系列函数上的Pareto前沿对比图Fig.3 Comparison diagram of Pareto frontier of the 3 algorithms on ZDT series functions

3.2.2 在DTLZ系列测试函数上的算法性能对比

在DTLZ系列测试函数上运行20 次，求取IGD指标和HV指标的平均值和标准差作为最终数据对比值来衡量算法的综合性，并与MOEA/D和MOEA/D-GR的算法进行对比。

由表2可知：通过对比MOEA/D，MOEA/D-GR和MOEA/D-SD的IGD均值和标准差可知，除测试函数DTLZ1和DTLZ3，MOEA/D-SD的IGD指标均值比MOEA/D和MOEA/D-GR小，说明算法性能要优于MOEA/D算法和MOEA/D-GR算法。除DTLZ3测试函数，MOEA/D-SD算法的IGD标准差值均小于MOEA/D和MOEA/D-GR算法，表明算法具有较好的鲁棒性。从表2中MOEA/D、MOEA/D-GR和MOEA/D-SD的HV指标均值对比数据可以看出：在DTLZ系列测试函数上MOEA/D-SD的HV指标均值大部分都比MOEA/D和MOEA/D-GR大，说明MOEA/D-SD的算法性能优于两种比较算法。图4是绘制的3 种算法的IGD盒图，从图4可以看出：MOEA/D-SD算法的其他测试函数的中位数大多高于两种比较算法；该算法的四分距相对其他两种对比算法较小，且该算法的异常点相对其他两种对比算法较少，证明了该算法具有较好的鲁棒性和精度。

表2 3 种算法在DTLZ测试函数上的指标对比Table 2 Index comparison of three algorithms on DTLZ test function

图4 3 种算法在DTLZ函数上运行20 次的IGD盒图Fig.4 IGD box graph with 3 algorithms running 20 times on DTLZ function

4 结 论

笔者提出的MOEA/D-SD算法通过衡量新解相对于旧解在收敛方向和多样性角度上的综合改进量来评估个体的进化状态，并根据个体进化状态的改进程度动态调节邻域大小，为每个子问题分配合适的邻域。将该算法与MOEA/D和MOEA/D-GR两种算法进行对比，从实验数据可知：算法的计算资源得到了有效分配，算法性能得到了有效提高。在接下来的工作中，可以考虑给每个子问题设置自适应分配邻域，并将其应用在高维多目标优化问题中。