大口径蝶阀流固耦合特性及共振特性的研究

2021-05-17张伟政赵鹏博张作丽刘仿民

振动与冲击 2021年9期

张伟政，赵鹏博，张作丽，刘仿民

(1.兰州理工大学石油化工学院，兰州 730050；2.温州伯特利阀门集团，浙江温州 325105)

三偏心金属硬密封蝶阀在石油、化工、冶金、水电等许多领域有广泛的应用，作为经济各领域中成套设备的关键产品,大口径、高温、高压三偏心金属硬密封蝶阀是国家重点攻关新产品[1]。目前，对大口径三偏心金属硬密封蝶阀的阀板和阀杆的应力变形及共振特性分析研究较少。陈宇政[2]采用计算流体动力学的方法对大口径蝶阀进行了流场和压力场计算。Lisowski等[3]利用CFD方法对控制阀内部流体进行了数值模拟分析。但是他们没有研究阀板和阀杆的具体应力和变形。此外，王雯等[4]利用流固耦合的方法对调节阀-管道-流体系统进行了动态特性研究。孟思佳等[5]利用流固耦合的方法对止回阀进行了流场及应力变形的数值模拟分析。赵永强等[6]利用流固耦合的方法对螺杆进行了不同工况下应力和变形分布规律。然而，针对大口径蝶阀的阀板和阀杆用流固耦合方法分析其应力和变形的研究较少。另外，还有一些学者研究了振动的问题。例如：刘文彬[7]利用数值模拟技术和实验相结合的方法对水管路阀门进行了振动噪声特性研究。王海民等[8]利用数值模拟、实验、经验公式相结合的方法进行了三偏心蝶阀的振动特性研究。Li等[9]利用热流固耦合的方法对连杆蝶阀进行了共振预测研究。这些研究对本论文的研究具有重要的理论指导意义，然而这些研究针对的都是口径比较小的阀，且这些研究没有进行不同开度下阀板和阀杆具体的共振分析。

本文通过研究大口径三偏心金属硬密封蝶阀5%、15%、30%、50%、75%和100%这6个开度来分析其流场特性，得出其流线云图，观察流线云图可知介质在流动过程中会有旋涡生成，当介质经过不同开度下的阀板和阀杆时会产生饶流，此时出现卡门涡街现象，当卡门涡脱落频率与阀板和阀杆的固有频率接近时，会发生共振。因此，本文也是利用这一理论知识来研究其共振特性。

1 几何模型及材料参数的确定

1.1 简化模型

利用solidworks软件建立其三维模型，为了提高计算精度，给阀门增加了管道，阀前取5DN，阀后取10DN，并且对模型进行了一些简化，如图1所示。

1-阀杆；2-阀板；3-管道；4-阀体图1 三偏心金属硬密封蝶阀Fig.1 Triple eccentric metal hard seal butterfly valve

1.2 材料参数的确定

在进行流固耦合分析时，静应力场需要确定阀门的材料参数，阀门的各部分零部件按照ASTM A216标准和ASTM A105标准来确定，如表1所示。

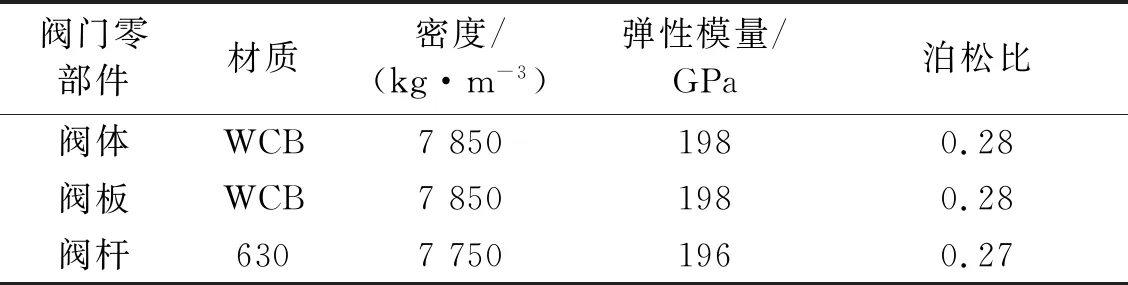
表1 阀门各部分零部件材质参数Tab.1 Material parameters of valve parts

1.3 工况的确定

本文采用的工况参数为：进口压力2 MPa，出口压力1.6 MPa，压降0.4 MPa，介质为液态水。

2 流固耦合数值模拟分析

2.1 流固耦合理论

流固耦合理论包含流场计算理论、静应力场计算理论和流固耦合计算理论三部分组成。

2.1.1 流场计算理论

由于三偏心金属硬密封蝶阀为湍流流动，因此采用标准Κ-ε模型来研究流场特性。本文所用到的流体力学控制方程有质量守恒方程、能量守恒方程和动量守恒方程。分别为

(1)

(2)

(3)

式中：k为传热系数;T为温度;Cp为比热容;ST为黏性耗散项;ρ为介质密度;u为介质流速;p为微元体上静压力;τij为应力张量;gi和Fi分别为i方向的重力和外部体积力，同时Fi包含源项。

2.1.2 静应力场计算理论

静应力场主要计算结构的应力和变形，因此采用流体引起固体振动和位移的控制方程为

(4)

式中：M为质量矩阵;C为阻尼矩阵;K为刚度矩阵;t为时间;r为结构变形;τ为结构应力;下标s为固体。

2.1.3 流固耦合计算理论

流固耦合系统也满足最基本的守恒原则，在耦合面处流体与固体的应力τ、位移d、热流量q和温度T等变量相等或守恒。其理论方程如下

(5)

式中：下标f代表流体;下标s代表固体。

2.2 流场模拟计算

2.2.1 流场内流道建立及网格划分

利用ANSYS软件DM模块对大口径三偏心金属硬密封蝶阀进行流道抽取，然后导入ANSYS ICEM CFD模块中进行网格划分，由于结构的复杂性，因此采用混合网格的方法来划分网格，两端圆管部分采用六面体结构化网格，中间阀门部分采用四面体非结构化网格。

2.2.2 网格无关性验证

表2 网格无关性验证Tab.2 Grid independence verification

由表2可知，当网格数从143万增加到175万时，进口质量流量增大了1.3%，出口平均流速增大了1.8%；当网格数从175万增加到209万时，进口质量流量增大了0.05%，出口平均流速减小了0.2%。由此可知，随着网格数的逐渐增大，进口质量流量的变化可以忽略不计，说明了网格对模拟计算没有影响，而为了考虑计算精度和计算资源，因此采用175万的网格数来计算。其他开度的网格生成方法和50%开度网格生成方法一样，网格数也在175万左右。

2.2.3 流场设置及结果讨论

利用ANSYS软件中的Fluent模块来进行流场计算分析，设置压力进口和压力出口为边界条件，壁面设置光滑无滑移，残差曲线精度设置为10-4。计算得出了5%、15%、30%、50%、75%和100%开度下的稳态流线云图。如图2所示。

图2 稳态流线云图Fig.2 Steady streamline nephogram

由图2可知，当三偏心金属硬密封蝶阀处于5%开度时，阀板左端上下部分有形成漩涡的趋势，而阀板右端流线呈螺旋状分布，流动情况比较紊乱；当蝶阀处于15%开度时，通过观察流体流线的动画运动方式发现阀板右端形成了一个巨大的漩涡，由碟板处出发，绕了一个圆周重新回到碟板处，然后再流向出口，流动状况比较紊乱；当蝶阀处于30%开度时，阀板右端中线处有杂乱的旋绕流动，漩涡开始减少；当蝶阀处于50%开度时，阀板右端出现少量的漩涡，然后流体流动开始趋于平稳；当蝶阀处于75%开度时，阀板右端能明显看出流体呈现交叉绕流，然后趋于平稳；当蝶阀处于全开时，阀板右端中线部分流动比较平稳，上下部分出现少量的紊乱流动。从这些流线图可以直观明显的看出流体在流过阀板时会产生漩涡，并且随着开度的增大，漩涡会减少，最终消失，并且流动状态也会趋于稳定。

2.3 静应力场模拟分析及结果讨论

利用ANSYS软件的static structural模块来进行静应力场分析，首先设置材料的性能等参数，然后通过mesh模块来对结构进行网格划分，对两端圆管部分采用六面体结构网格的方法划分，中间阀门部分采用自适应网格划分的方法来划分网格，通过控制网格的大小来对阀板和阀杆进行网格重新划分，以提高其网格精度。经过网格无关性验证，最终确定网格数为598 866，节点数为949 220。此时把流场的计算结果导入静应力场的setup模块中，然后进行固定约束设置等操作，求解后得出不同开度下的变形云图和等效应力云图。当阀门处于5%开度和15%开度时，阀板和阀杆的变形云图和等效应力云图如图3所示。

图3 阀板和阀杆的变形云图和等效应力云图Fig.3 Deformation nephogram and equivalent stress nephogram of valve plate and valve stem

从图3中可以看出，在5%开度下，阀门的最大变形主要集中在阀板开启的一端，最大变形量为0.75 mm，造成这样的原因是因为在阀门刚开启的时候，小开度的情况下，阀板开启的一端会承受流体较大的压差，所以会导致阀板开启的一端出现较大的变形。而阀门的最大应力主要集中在靠近阀杆上端的阀板处，最大应力值为184 MPa。造成这样的情况是因为在阀板开启的过程中，阀板的上端面与阀座在开启的瞬间会产生较大的刮擦现象，所以会导致那个部位出现较大的应力。在15%开度下，阀门的最大变形还是集中在开启的一端，最大变形量为1.03 mm，造成这样的原因是因为随着阀门开度的逐渐增大，阀门开启的一端所承受的流体冲击力逐渐变大，相对应变形也会变大。而阀门的最大应力主要集中在阀杆的下端处，最大应力值为294 MPa。造成这样的原因是随着阀门开度逐渐增大的过程中，在开启一端阀杆和阀板的下端处，由于流速面积由小变大，流速由最大变小，阀杆的底部承受了较大的压差，所以才会出现这样应力集中的分布状况。

此外，为了反映阀门不同开度时的变形和应力情况，将阀板和阀杆的最大应力和最大变形数据绘制成相关曲线，分别如图4和图5所示。

近年来，全球的制造业正在迈向数字化时代。数字化进程正在改变产业链的每个环节：从研发、供应链、工厂运营到营销、销售和服务。生产商、消费者以及工业实物资产之间的数字化链接将释放出巨大的价值，并彻底刷新制造业的版图。面对这一转变，越来越多的公司进行IT和OT的融合，通过设备、人与服务的互联互通，将传统的工厂升级为数字化工厂，从研发，到制造，再到后期运维，甚至是产品都能做到可视化，让制造过程透明化。未来制造企业的数字化工厂要包含三部分：一是智能化的生产过程；二是智能化的仓储物流；三是智能加工中心的生产线。与此同时，自动化企业也相继在进行向数字化工厂的转变。

从图4可以看出，5%开度时，最大等效应力值为185 MPa，是所有开度中的最低值；75%开度时，最大等效应力值为761 MPa，是所有开度中的最高值。从全关到全开时，随着开度的逐渐增大，最大等效应力逐渐增大，在75%开度时达到最大，然后再随着开度的增大，最大等效应力开始逐渐减小。从图5可以看出，最大轴向变形的范围在0.5～3 mm，75%开度时，轴向最大变形最大，变形量为2.85 mm；全开时，轴向最大变形最小，变形量为0.7 mm。从全关到全开时，随着开度的逐渐增大，轴向最大变形开始逐渐增大，到75%开度时变形量达到最大，然后变形量开始随着开度的增大而减小。造成上述情况的原因是因为，随着开度的不同，阀板和阀杆周围流体流动的区域、流速不同，所以才会出现这样的情况。图4和图5表明，阀板和阀杆在75%开度时，最大等效应力和轴向最大变形达到最大值，为了减小阀板和阀杆的应力和变形，应尽量少在75%开度下运行。

图4 最大等效应力曲线图Fig.4 Maximum equivalent stress curve

3 共振特性分析

利用模态分析可以确定一个结构的固有频率和振型，而利用谐响应分析可以得到响应值对应频率的曲线，可以有效的预测结构的持续动力学特征。本文只考虑了阀板和阀杆在流固耦合的物理场情况下，利用预应力模态分析得出其固有频率，和通过计算流体流过阀板时的脱落涡频率，当两者频率接近时会发生共振现象。并且利用谐响应分析来得到其频率对应响应值的曲线来研究阀门的共振特性。

3.1 模态分析

3.1.1 模态分析理论

一般情况下，结构的振动模态，只考虑空载的情况下，而有些结构需要在一些耦合场下工作，因此其振动模态要考虑这些耦合场下一些载荷的影响。振动模态的理论方程为

(6)

式中:ωi为振动频率;φi为模态;[K]为刚度矩阵;[M]为质量矩阵。

3.1.2 固有频率求解及分析

运用ANSYS软件对结构模型进行数值分析计算求解，得到了5%开度和15%开度的前两阶振型图，如图6所示。

图6 5%开度和15%开度前两阶振型图Fig.6 The first two mode shapes of 5% opening and 15% opening

从图6中可以看出，当阀门位于5%开度时，阀板和阀杆一阶模态的最大变形量为0.146 04 mm，最小变形量为0.140 57 mm，而阀板和阀杆的二阶模态的最大变形量为0.143 68 mm，最小变形量为0.138 26 mm。当阀门开度位于15%开度时，阀板和阀杆的一阶模态的最大变形量为0.147 78 mm，最小变形量为0.140 13 mm，而阀板和阀杆的二阶模态的最大变形量为0.144 66 mm，最小变形量为0.137 56 mm。一阶模态量与二阶模态变形量差距不大，可能与流体在结构上的作用力大小有关。而其他开度下的振型模态与5%开度和15%开度下的振型模态类似。

为了反映阀门不同开度下阀板和阀杆的振动模态最大变形量和最小变形量之间的关系，列出了各个阀门开度下前两阶的模态变形量，如表3所示。

表3 不同开度下前两阶的振动模态变形量Tab.3 Modal deformation of the first two steps under different opening

从表3中可以看出，随着阀门开度的逐渐增大，阀板和阀杆的前两阶最大变形量开始逐渐增大，而阀板和阀杆的前两阶最小变形量开始逐渐减小。同一开度下，一阶的振动模态最大、最小变形量大于二阶振动模态的最大、最小变形量。当阀门位于5%开度时，一阶振动模态最大变形量达到最小值0.146 04 mm和最小变形量达到最大值0.140 57 mm；阀门位于全开时，一阶振动模态最大变形量达到最大值0.156 85 mm和最小变形量达到最小值0.131 69 mm。造成上述情况的原因是随着阀门开度的变化，流体流过阀板和阀杆时，阀板周围的流动状态不同，流速也不同，脱落涡的运动方式也不同。当处于小开度时，阀板下端的流速面积小，流速快，压强小，脱落涡逐渐形成，涡的脱落对于阀板的下端处撞击较小，而阀板的结构是中间厚，边缘薄，因此最大变形量出现在阀板的边缘处，相应的最大变形量也会较小；而随着阀门开度的逐渐增大至全开时，流体的流速面积逐渐增大，阀板的下端位置流速低于阀板两侧的流速，此时阀板下端会产生较大的压强，因此全开的时候下端处的最大变形量会达到最大。

同时，为了能够更清楚的显示阀门开度和固有频率等数据的关系，列出了前六阶不同开度下的固有频率，如表4所示。

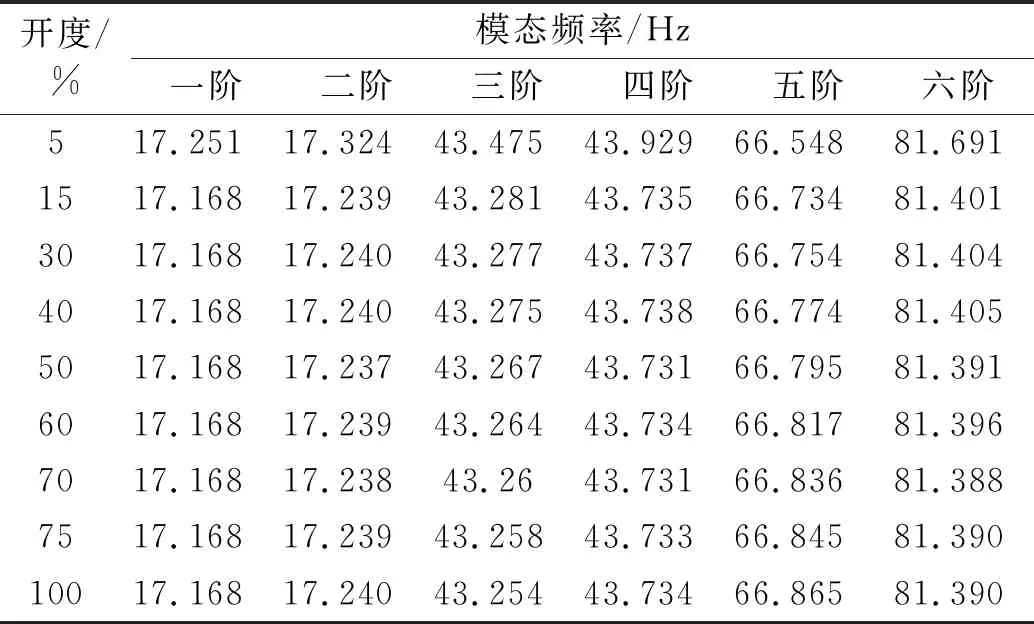
表4 不同开度下前六阶固有频率Tab.4 The first six natural frequencies under different opening degrees

从表4可以看出，当阀门位于5%开度时，一阶模态的固有频率是最大的，而随着开度的逐渐增大，一阶模态的固有频率都是一样的。而同一开度下随着模态阶数的增加，固有频率是逐渐增大的。此外，随着开度的逐渐增加，五阶模态的固有频率是逐渐增大的，而其他阶模态频率相对是减小的。造成上述情况的原因是随着阀门开度的变化，流体流过阀板和阀杆时的流动状态发生改变，此时形成的脱落涡的位置相应也会发生改变，涡的脱落作用在阀板和阀杆的位置就会发生变化，从而出现这样的情况。

3.2 卡门涡理论及脱落涡频率计算

当来流绕过某些物体时，物体两侧会周期性地脱落出旋转方向相反、排列规则的双列线涡，经过非线性作用后，形成卡门涡街。卡门涡的涡脱频率与物体形状，来流速度，物体几何特征尺度有关[10]，当涡脱频率与蝶板的固有频率接近时会发生共振现象，需要求得卡门涡的脱落频率。根据卡门涡的经验计算公式[11]计算出脱落涡频率Fk。其公式为

(7)

式中:Fk为卡门涡脱落频率(Hz);St为斯特罗哈数;ν为流经阀板的水流速度(m/s);T为出水边厚度(m)。

对于44 mm厚的阀板，流经阀板的水流速度会随阀门开度的变化而变化，而斯托罗哈数仅与Re有关。雷诺数的计算公式为

(8)

式中:ρ为流体密度(kg/m3);ν为流体平均流速(m/s);d为管公称直径(m);μ为流体动力黏度(Pa·s)。

根据雷诺数计算公式可以求出不同开度下相对应的斯托罗哈数，根据式(7)代入数据可以得出脱落涡频率。

3.3 结果对比分析

根据上述经验公式计算了5%、15%、30%、40%、50%、60%、70%、75%和100%开度下的脱落涡频率，把不同开度下计算出来的脱落涡频率与模拟出来的模态频率数据绘制成曲线图，如图7所示。

图7 不同开度下阀板和阀杆的脱落涡频率计算值与模态频率模拟值对比曲线图Fig.7 Comparison between calculated value of vortex frequency and simulated value of modal frequency of valve plate and valve stem under different opening

通过图7可知，当阀门位于5%和15%开度时，模拟值与计算值差距较大，不会发生共振；而当阀门位于30%开度时，一、二阶模态值与计算值相近，阀板和阀杆可能会发生共振；当阀门位于50%开度时，三、四阶模态值与计算值基本重合，阀板和阀杆会发生共振；当阀门位于75%和100%开度时，计算值分别与其六阶模态值和十四阶模态值有些差距，发生共振的可能性很小。

3.4 谐响应分析

利用workbench模态叠加法进行了谐响应分析，设定其频率求解范围为0～100 Hz，运算次数为“100”，即每隔1 Hz求解一次。对阀板和阀杆轴向施加2 MPa的压力为简谐激振力，设置阀板和阀杆为响应体，得到了30%开度和50%开度下阀板和阀杆的位移响应-频率曲线，分别如图8(a)和(b)所示。

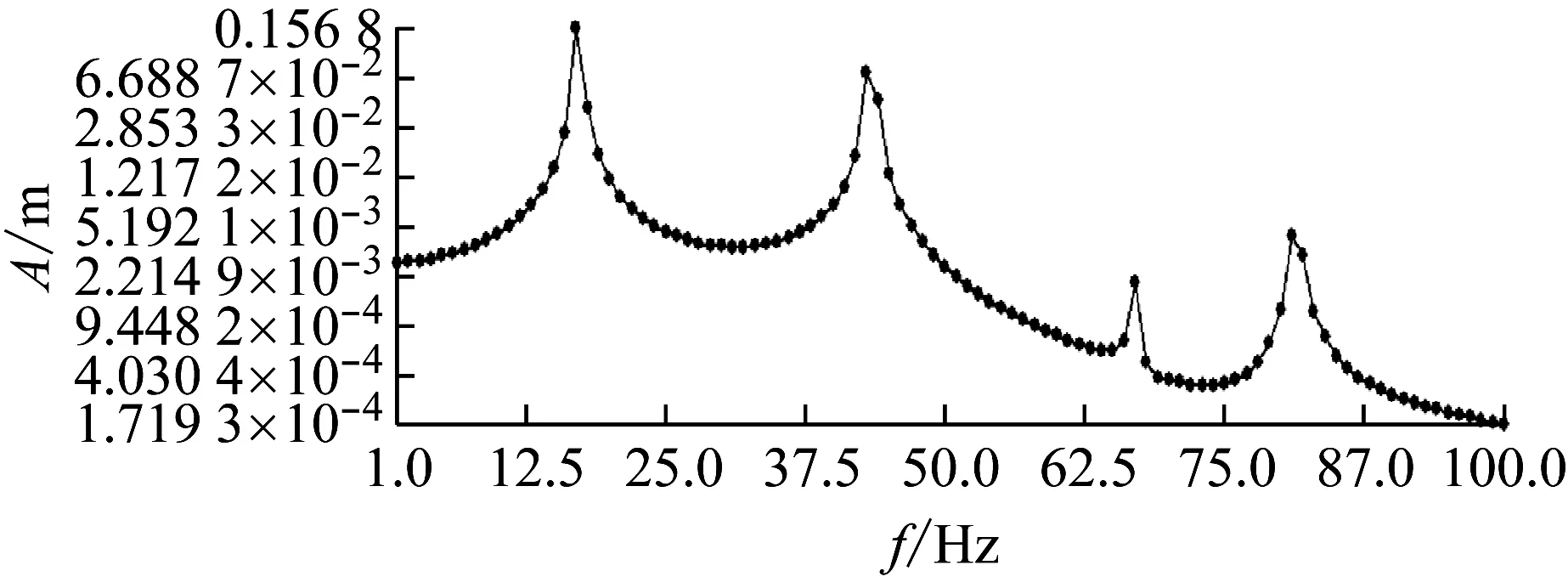
(a) 30%开度位移响应-频率曲线

分析图8位移响应-频率曲线可知：当阀门位于30%开度和50%开度时，在18 Hz和43 Hz附近处出现两个波峰，其刚好对应两个开度下前四阶的固有频率分布位置。此时，阀门会出现共振，响应幅值最大。其符合了结构的动力学特征，同时也验证了对结构固有频率计算的准确性。通过图8还可以看出，阀门在30%开度时，频率位于18 Hz处，结构发生共振，振幅最大为0.15 mm；阀门在50%开度时，频率位于43 Hz处，结构发生共振，振幅为0.22 mm。从这可以验证上述脱落涡频率与结构固有频率发生共振结果的准确性。通过文献[8]可知，前人用实验方法测的结果与数值模拟结果接近，也侧面验证了数值模拟结果的准确性。因此，可以认为本论文的研究具有可靠性。而为了避免阀板和阀杆因共振现象而出现损坏，影响其运转，阀门工作时应该避免在这两个开度下，其相应的频率范围内工作。