齿廓修形人字齿轮副时变啮合刚度计算方法

林腾蛟，陈梦寒，杨 金

(重庆大学 机械传动国家重点实验室，重庆 400044)

人字齿轮具有高重合度、低轴向力、高承载能力和平稳传动等优点，广泛应用于航空航天、大型船舶等重要传动装置中。人字齿轮运转过程中，轮齿交替啮合，导致啮合冲击及接触刚度变化，影响传动系统动态性能。时变啮合刚度是齿轮系统振动噪声的重要激励因素，齿廓修形在有效改善轮齿啮合性能的同时，对其时变啮合刚度也将产生较大影响，因此开展修形人字齿轮副时变啮合刚度解析算法研究对人字齿轮系统动力学精准分析具有重要的理论及工程意义。

近年来，国内外学者在轮齿修形及时变啮合刚度研究方面取得了诸多成果。Litvin等[1-2]改变标准齿条刀具切削刃，采用修形曲线代替齿条直线齿廓，获得修形齿轮齿面方程；唐进元等[3-5]采用有限元法研究了修形直齿轮的啮合刚度；Sun等[6]在基于切片法的啮合刚度算法中引入有限元法与解析算法间误差的修正系数，建立了修形直齿轮副啮合刚度准确计算模型；Wan等[7-8]采用积分势能法计算了斜齿轮的啮合刚度；魏静等[9-11]将齿顶修形等效为轮齿误差，提出了齿廓修形齿轮的啮合刚度计算方法；王成等[12-13]将齿顶修形量表示为啮合线长度的函数，建立了考虑齿顶修形的直齿轮啮合刚度计算模型。在人字齿轮啮合刚度计算方面，王峰等[14]基于齿面LTCA方法，以啮合刚度波动幅值为目标，对人字齿轮进行了齿面修形优化设计；郭家舜等[15]将齿廓修形作为沿啮合线方向的时变间隙，研究了修形参数对人字齿轮副动载系数幅值的影响规律。以上文献取得了重要研究成果，但主要针对修形直、斜齿轮啮合刚度，解析算法中多将修形量等效为误差或间隙等因素；目前涉及人字齿轮啮合刚度的研究报道较少，且均未同时考虑修形轮齿的齿廓几何特征、重合度变化以及退刀槽对人字齿轮啮合刚度的影响。

本文以人字齿轮副为研究对象，提出一种计及齿廓修形参数和退刀槽宽度的人字齿轮时变啮合刚度计算方法。建立含齿顶和齿根修形的人字齿轮齿面方程，分析轮齿修形和受载变形对齿轮重合度和接触状态的影响；基于势能法和数值积分公式，推导人字齿轮端面啮合刚度和轴向啮合刚度，并研究退刀槽宽度、修形参数、输入转矩等对人字齿轮时变啮合刚度的影响规律。

1 齿廓修形人字齿轮齿面方程推导

1.1 刀具端面齿廓方程

轮齿齿廓修形包括齿顶和齿根修形，为建立修形齿廓的齿面方程，采用假想刀具加工轮齿，假想刀具齿廓由4段曲线组成，如图1所示，其中直线1(CD段)、曲线2(DE段)、曲线3(BC段)和椭圆弧4(AB段)分别包络出被加工齿轮的渐开线区、齿顶修形区、齿根修形区和过渡圆弧区，曲线2、3的方程为y=axn，a为修形曲线系数，由修形参数确定，n为修形曲线的阶次。

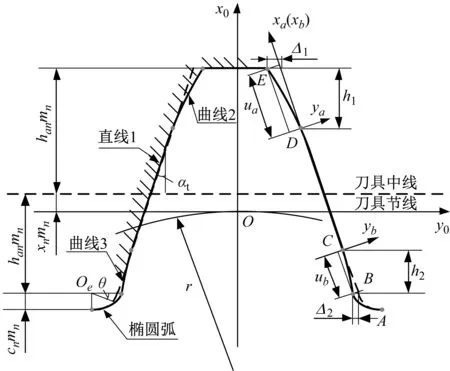
图1 假想刀具端面齿廓Fig.1 Transverse profile of hypothetical rack cutter

图1中S0(x0Oy0)为假想刀具端面齿廓坐标系，Sa(xaOaya)和Sb(xbObyb)分别为曲线2、3的局部坐标系。通过坐标变换，可得端面齿廓上各曲线对应的方程RS0,i(i=1～4)，分别表示为

(1)

式中：l1为CD上任意点到D点的距离；αt为端面压力角；“+”号用于刀具右齿面，“-”号用于刀具左齿面。

(2)

RS0,3(Δ2,h2,n)=

(3)

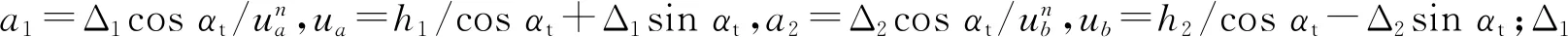
(4)

式中：xOe和yOe为椭圆弧圆心坐标；c1和d1分别为椭圆弧长半轴和短半轴；θ为椭圆弧段角度变量。

图2为假想刀具与被加工齿轮坐标系位置关系，其中假想刀具1加工出人字齿轮的右旋齿面，刀具2加工出左旋齿面，由坐标变换得到S1(x1O1y1)坐标系中刀具齿面方程RS1,i

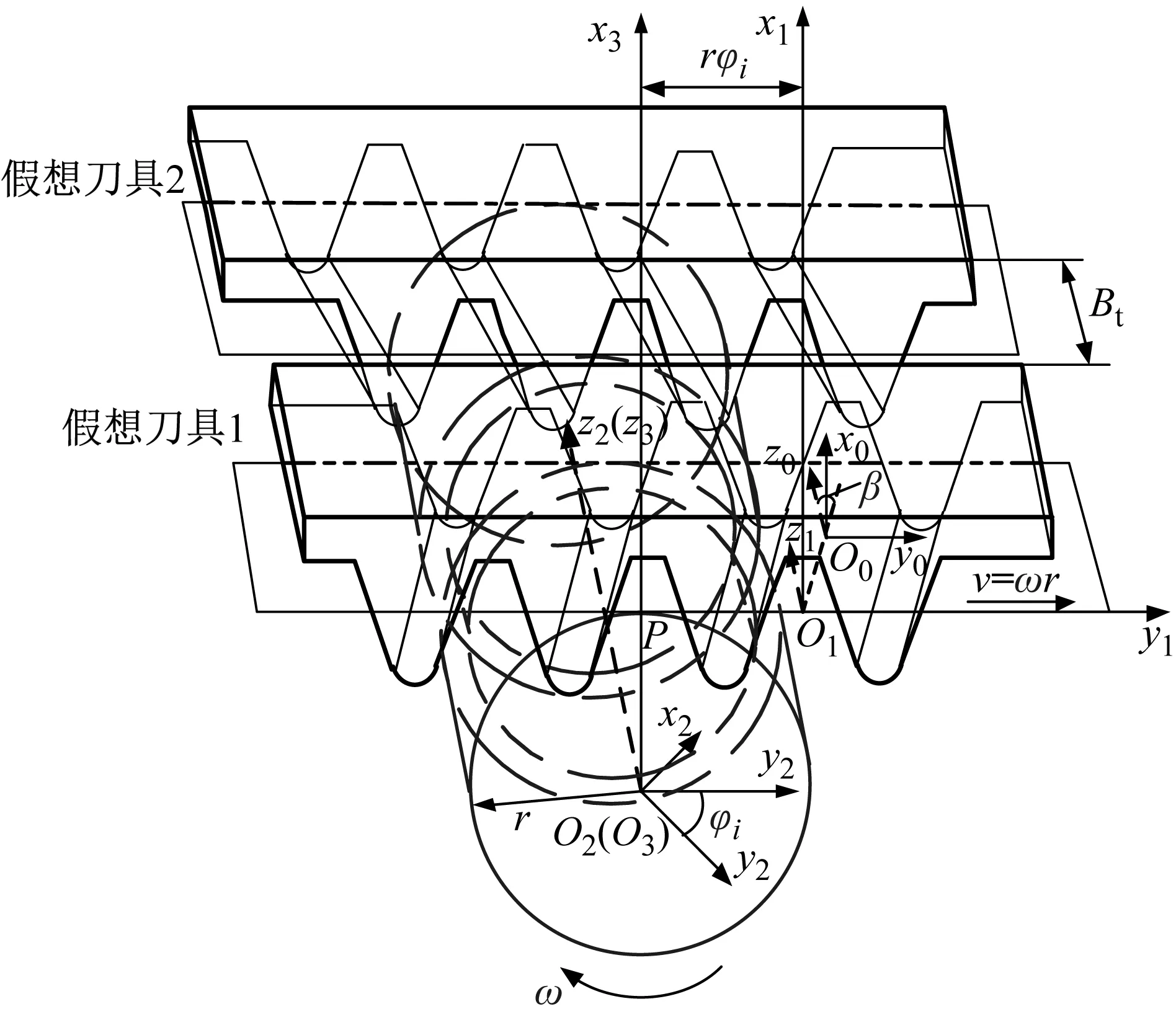
图2 假想刀具与被加工齿轮坐标系Fig.2 Coordinate systems of hypothetical rack cutter and machined gear

RS1,i=M10RS0,i

(5)

式中：M10为S0到S1的坐标变换矩阵。

1.2 齿轮齿面方程

根据假想刀具与被加工齿轮在齿面上任意点的正确啮合条件n·v=0，推导出含齿廓修形的人字齿轮在S2(x2O2y2)坐标系中的齿面方程RS2,i

(6)

式中：RS1,ix、RS1,iy、RS1,iz分别为S1坐标系中刀具齿面方程x、y、z分量；φi为形成被加工齿轮齿面时S2坐标系的转动角度；r为被加工齿轮的节圆半径。

2 齿廓修形人字齿轮时变啮合刚度计算原理

人字齿轮由左右两侧斜齿轮和退刀槽构成，在工程实践中人字齿轮的支撑方式通常为主动轮采用轴向可浮动的轴承支撑，从动轮采用能承受少量轴向载荷的轴承支撑，以满足左右两侧斜齿轮均载要求，而航空航天、大型船舶等重要传动装置中人字齿轮制造加工精度较高，啮合过程中人字齿轮轴向窜动量较小，齿面啮合状态良好，本文在研究人字齿轮时变啮合刚度时假定齿面啮合为理想接触，在啮合过程中左右两侧斜齿轮同时参与啮合。轮齿啮合刚度是随参与啮合齿数和轮齿接触位置周期变化的时变函数，齿轮接触线长度具有时变性，由于人字齿轮的接触线与轴线不平行，单侧斜齿轮在啮合过程中受轴向力作用，因此齿轮啮合刚度需按端面啮合刚度和轴向啮合刚度分别计算。

当人字齿轮存在退刀槽时，退刀槽的变形会引起轮齿啮合刚度变化，因此计算人字齿轮副啮合刚度时还需要计及退刀槽的影响。

将轮齿变形等效为沿啮合线方向的弹性变形，在啮合力F作用下，综合考虑轮齿发生的端面变形、轴向变形以及包含退刀槽在内的基体变形而储存的弹性势能可表示为[16]

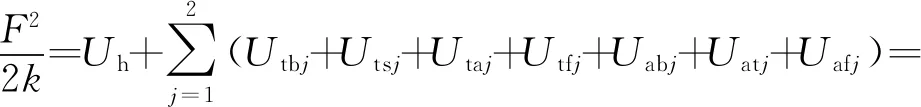
(7)

因此啮合周期内一对轮齿的啮合刚度，即单齿啮合刚度表示为

(8)

式中：j=1、2，分别表示主、从动轮；Utb、ktb为端面弯曲势能和刚度，Uts、kts为端面剪切势能和刚度，Uta、kta为径向压缩势能和刚度，Utf、ktf为基体径向势能和刚度，Uab、kab为轴向弯曲势能和刚度，Uat、kat为轴向扭转势能和刚度，Uaf、kaf为基体轴向势能和刚度，Uh、kh为赫兹接触势能和刚度。

2.1 端面啮合刚度

齿轮端面啮合刚度包括啮合力F作用下的轮齿弯曲刚度、剪切刚度、径向压缩刚度、赫兹接触刚度和基体径向刚度五部分。计算人字齿轮端面啮合刚度时，基于势能法和切片思想，将轮齿沿齿宽方向切片，见图3，通过计算各薄片啮合刚度，求和可得齿轮端面啮合刚度。修形薄片轮齿的悬臂梁模型如图4所示。

图3 轮齿切片模型Fig.3 Slice model of tooth

图4 齿廓修形薄片轮齿悬臂梁模型Fig.4 Cantilever beam model of tooth slice with profile modification

采用切片法时，厚度为Δz的每一薄片轮齿中端面弯曲势能、端面剪切势能和端面压缩势能分别表示为

(9)

(10)

(11)

式中：Mt为啮合力F作用下轮齿端面所受弯矩，Mt=Fcosβ[cosαz(x(αz)-x)-sinαzy(αz)]；x(αz)、y(αz)分别为薄片轮齿啮合点坐标值，由齿面方程(6)计算可得；nS2,x(αz)、nS2,y(αz)为薄片轮齿啮合点处齿面法矢的x、y分量；Δz为薄片轮齿齿宽，Δz=(2B+Bt)/N，B为单侧斜齿轮齿宽；Bt为退刀槽宽度；N为人字齿轮沿齿宽方向切分的薄片份数；αz为每片薄片轮齿啮合点处的端面压力角，αz=arctan(nS2,x(αz)/nS2,y(αz))；β为螺旋角；E、G表示齿轮材料的弹性模量和剪切模量。

对每一薄片齿轮刚度沿人字齿轮的齿宽方向求和，得到人字齿轮的端面弯曲刚度、端面剪切刚度、径向压缩刚度分别为

(12)

(13)

(14)

对于每一薄片轮齿，由于所处轴向位置不同，轮齿啮合位置也不同，各薄片轮齿上啮合点的坐标值x(αz)、y(αz)和压力角αz是关于轴向位置z和啮合时间t的函数，如图5所示，其应满足

图5 任意时刻薄片轮齿啮合状态示意图Fig.5 Sketch map of meshing state of tooth slice at any time

(15)

(16)

(17)

0≤l(t)≤εαpbt

(18)

式中：“+”号用于主动轮，“-”号用于从动轮；v=2πnjrbj，nj为齿轮的转速，rbj为齿轮基圆半径；εα为齿轮端面重合度；rsj表示端面啮合起始点到齿轮圆心的距离，rtj表示任意时刻端面啮合点到齿轮圆心的距离；βb为基圆螺旋角；pbt为端面基圆齿距。

当薄片轮齿上的αz、x(αz)、y(αz)不满足式(15)～(18)时，此薄片轮齿未参与啮合。

人字齿轮赫兹接触势能和接触刚度分别为

(19)

(20)

式中：μ为齿轮材料泊松比，L为接触线长度。

对每一薄片齿轮基体径向势能和基体径向刚度沿齿宽方向进行求和，即可得到齿轮基体的径向势能和径向刚度，其表达式分别为

(21)

(22)

式中：L*，M*，P*，Q*为尺寸系数[17]，uf，Sf如图4中所示，可表示为

(23)

式中，Z为齿轮的齿数。

2.2 轴向啮合刚度

人字齿轮轴向啮合刚度包括轮齿的轴向弯曲刚度、轴向扭转刚度以及基体的轴向刚度。假设接触线上所受的啮合力相等，齿轮在轴向力作用下绕Y轴的弯矩Ma和绕X轴的扭矩MT，如图6所示，可分别表示为

图6 人字齿轮轴向啮合刚度计算模型Fig.6 Axial mesh stiffness calculation model of double helical gear

(24)

式中,Ns表示参与啮合的轮齿薄片数量。

由于单侧斜齿轮的轴向力会使轮齿产生轴向弯曲变形和扭转变形，因此人字齿轮轮齿的轴向啮合刚度同样包括轴向弯曲刚度和轴向扭转刚度。啮合力F作用下，轮齿轴向弯曲势能和轴向扭转势能表示为

(25)

(26)

(27)

基于势能法，轮齿的轴向弯曲刚度和轴向扭转刚度可表示为

(28)

(29)

在两侧斜齿轮的啮合力作用下，含退刀槽的人字齿轮基体部分会产生弯曲变形，基体的轴向弯曲势能可表示为

(30)

式中：Maf为作用于齿轮基体的弯矩，Iaf为基体距离齿轮中心x1处的截面惯性矩，其表达式分别为

(31)

(32)

式中:rf为齿根圆半径;r0为齿轮轴孔半径;rt为退刀槽外圆半径。

因此人字齿轮基体的轴向刚度可表示为

(33)

3 考虑受载变形的修形人字齿轮啮合特性

齿轮修形参数与传递载荷有关，在实际运行工况下，合理的轮齿修形可有效降低啮合冲击，提升齿轮系统运转平稳性，但轮齿修形和受载变形会导致齿轮副重合度的变化，进而影响齿轮时变啮合刚度，即齿轮副在啮合过程中同时啮合的轮齿在单位齿宽上的单齿啮合刚度之和，因此有必要对轮齿受载变形下的齿廓修形人字齿轮啮合状态和时变啮合刚度进行分析。

3.1 修形人字齿轮副的啮合起止点

为研究受载变形下齿廓修形人字齿轮副的啮合状态，需确定实际载荷作用下轮齿的端面啮合起止点。人字齿轮同时有多对轮齿参与啮合，基于修形齿轮的啮合力F和单齿啮合刚度k，参与啮合的各对轮齿沿啮合线方向的变形δ(αz)可表示为

(34)

式中：km(αz)为第m对参与啮合的单齿啮合刚度；Nc为参与啮合的轮齿对数。

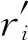
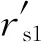
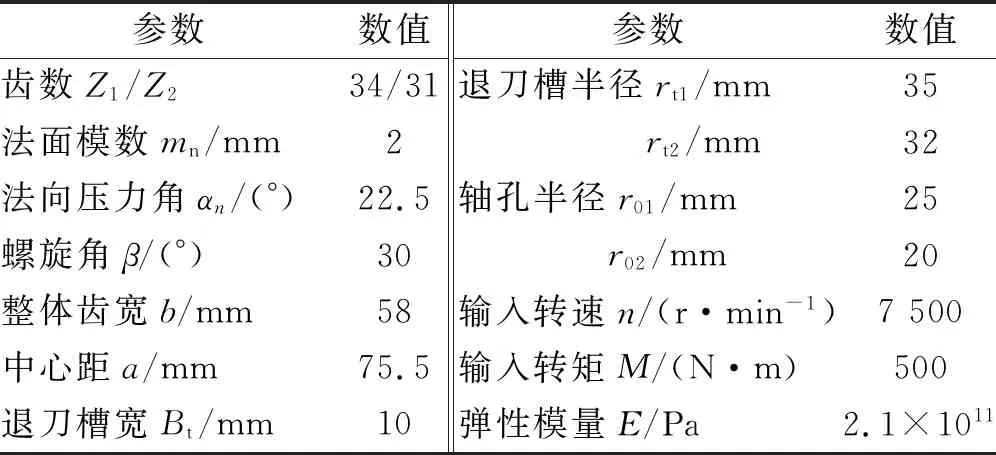
表1 人字齿轮副基本参数Tab.1 Basic parameters of double helical gear pair

为验证啮合起止点计算方法的准确性，根据文中推导的齿廓修形人字齿轮齿面方程，利用ANSYS软件建立修形人字齿轮副静力接触有限元分析模型，对主动轮内圈节点施加转矩，并约束其轴向和径向位移；对从动轮内圈节点施加全约束，求解得到轮齿的接触状态如图8所示，提取主动轮啮合起止点处结点坐标，得出轮齿啮合起止点到主动轮圆心的距离分别为38.004 mm和41.226 mm，与图7解析法计算结果对比，两者误差分别为0.32%和0.47%，验证了实际啮合起止点计算方法的准确性。

图7 修形齿轮啮合起止点计算流程图Fig.7 Flow chart of calculating meshing start and end points of gear with modification

3.2 修形人字齿轮副的重合度

图9给出了修形人字齿轮副的实际端面重合度计算示意图，图中B2、B1为未修形时齿轮端面啮合起止点，C2、C1为修形后齿轮端面啮合起止点。

图9 齿廓修形齿轮副端面重合度计算示意图Fig.9 Sketch map of contact ratio calculation of gears with profile modification

修形人字齿轮的端面重合度可表示为

(35)

式中,u为传动比。

由于本文只对人字齿轮进行了齿廓修形，对人字齿轮的纵向重合度不产生影响，则纵向重合度为[18]

(36)

因此齿廓修形人字齿轮副的总重合度为

(a) 等效应力云图

(37)

3.3 人字齿轮副时变啮合刚度

由于轮齿受载变形后修形人字齿轮接触状态和重合度发生变化，轮齿的接触线长度也会随之变化，考虑轮齿受载变形后修形人字齿轮的时变接触线长度L可表示为

L(F,Δ,h,n)=

(38)

L(F,Δ,h,n)=

(39)

考虑轮齿受载变形时，根据轮齿的实际啮合起止点，齿轮副啮合刚度计算的积分域应满足

(40)

为了验证含修形人字齿轮啮合刚度解析算法的正确性，利用文中所给算法和有限元数值方法分别计算修形人字齿轮副的啮合刚度，两者的计算结果如图10所示，图中横坐标T为无量纲时间，表示轮齿从啮入到啮出的整个过程。

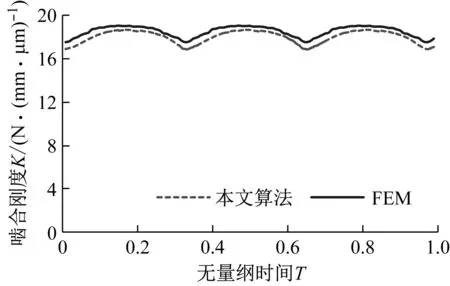
图10 人字齿轮副的啮合刚度对比曲线Fig.10 Comparison curves of double helical gears mesh stiffness

对比人字齿轮副时变啮合刚度解析算法和有限元数值法的计算结果，两者吻合良好，啮合刚度变化规律一致，两者计算所得人字齿轮副啮合刚度的均值分别为17.885 N/(mm·μm)和18.570 N/(mm·μm)，误差为3.83%，在工程允许范围内。

4 人字齿轮啮合刚度影响因素分析

针对表1所示的人字齿轮副，研究退刀槽宽度、修形量、修形长度、修形曲线阶次、输入转矩对人字齿轮副重合度和时变啮合刚度的影响规律。

4.1 退刀槽宽度

在修形参数和输入转矩保持不变情况下，保持单侧轮齿宽度不变，选取退刀槽宽度Bt的变化范围为0～40 mm，计算可得不同退刀槽宽度时人字齿轮副的重合度和啮合刚度变化规律如表2和图11所示。随着退刀槽宽度的增大，人字齿轮的基体刚度增大，齿轮副啮合刚度随之增大；由于改变退刀槽宽度并不影响人字齿轮副的重合度，啮合刚度波动值变化不大。

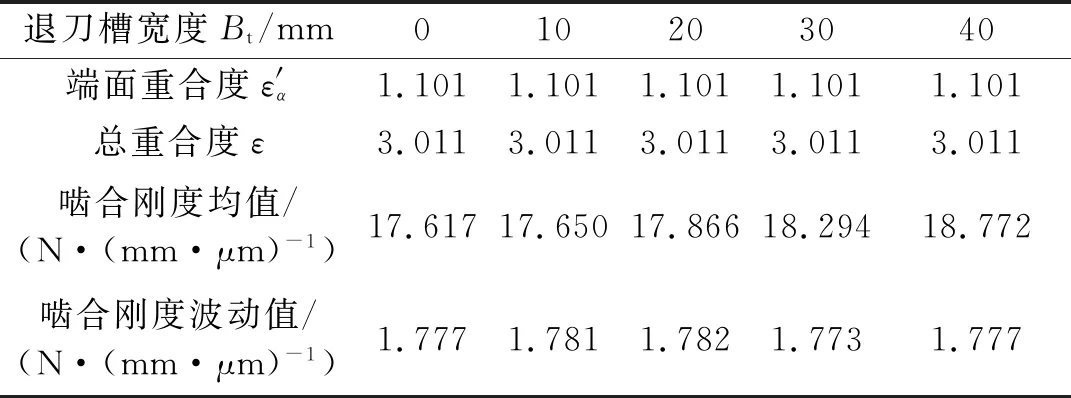
表2 不同退刀槽宽度下的人字齿轮重合度及啮合刚度Tab.2 Contact ratio and mesh stiffness of double helical gears with different width of run-out groove

4.2 修形量

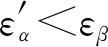
其他参数保持不变，选取主、从动轮齿顶和齿根修形量变化范围为0～15 μm，计算得到不同修形量时人字齿轮副的重合度和啮合刚度变化规律如表3和图12所示。齿廓修形后齿顶和齿根修形区齿厚减薄，轮齿刚度减弱，在输入转矩作用下齿轮部分修形区参与啮合，齿轮重合度有所减小，致使修形齿轮啮合刚度小于未修形齿轮。随着修形量的增大，轮齿齿厚削弱程度增加，轮齿修形区参与啮合的区域减小，齿轮副重合度减小，啮合刚度均值减小，啮合刚度波动值随之变化，当齿轮副总重合度接近整数时，啮合刚度波动值相对较大，而当端面重合度接近整数时，啮合刚度波动值相对较小。当修形量过大时，齿轮副端面重合度小于1，可能引起啮合冲击，降低传动的平稳性。

图12 不同修形量时人字齿轮副的啮合刚度Fig.12 Mesh stiffness of double helical gears with different profile modification amount

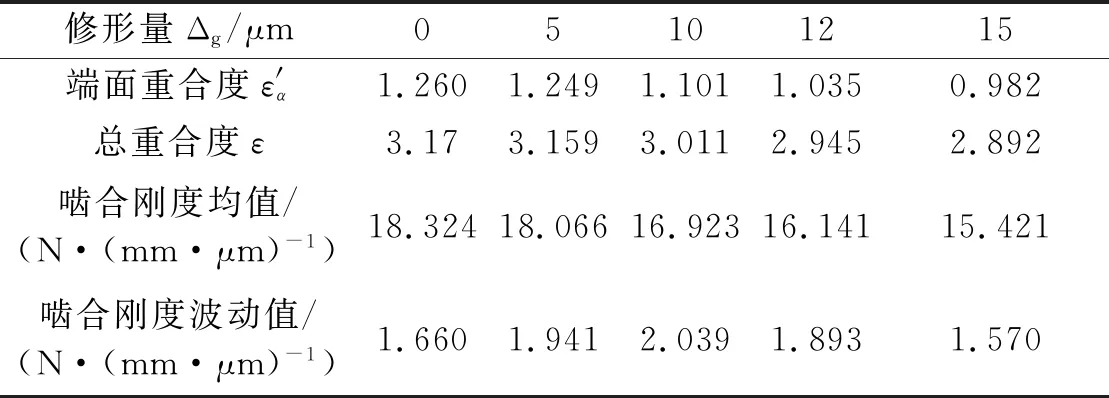
表3 不同修形量时人字齿轮副的重合度及啮合刚度Tab.3 Contact ratio and mesh stiffness of double helical gears with different profile modification mount

4.3 修形长度

其他参数保持不变，选取主、从动轮的齿顶和齿根修形长度变化范围为0.6～1.2 mm，计算得到不同修形长度时人字齿轮副的重合度和啮合刚度变化规律如表4和图13所示。随着修形长度的增大，齿廓修形区域增大，相同载荷作用下，轮齿啮合区域减小，齿轮副重合度降低，导致接触线长度减少，啮合刚度均值减小，啮合刚度波动值随之变化，当修形长度为1 mm时，齿轮副总重合度最接近于整数3，啮合刚度的波动值较大。

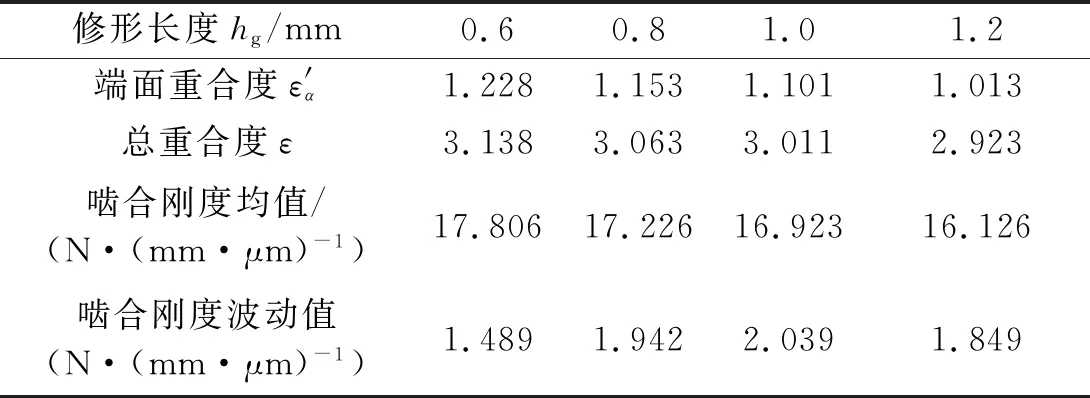
表4 不同修形长度时人字齿轮副的重合度及啮合刚度Tab.4 Contact ratio and mesh stiffness of double helical gears with different profile modification length

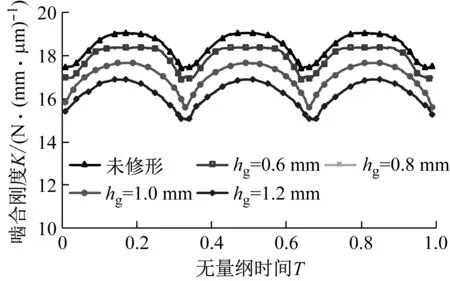
图13 不同修形长度时人字齿轮副的啮合刚度Fig.13 Mesh stiffness of double helical gears with different profile modification length

4.4 修形曲线阶次

其他参数保持不变，选取主、从动轮的齿顶和齿根修形曲线阶次分别为2、3、4和6，计算可得不同修形曲线阶次时人字齿轮副的重合度和啮合刚度变化规律如表5和图14所示。随着修形曲线的阶次增大，修形区域的齿廓曲率增大，轮齿齿厚削弱程度减小，相同载荷作用下，齿轮副的重合度增大，啮合刚度均值随之增大。当修形曲线阶次大于4时，由于修形量一般为微米量级，而修形曲线曲率变化很小，齿轮副重合度变化也很小，此时啮合刚度均值和波动值随修形曲线阶次的变化不大。

表5 不同修形曲线阶次时人字齿轮副的重合度及啮合刚度Tab.5 Contact ratio and mesh stiffness of double helical gears with different profile modification curve

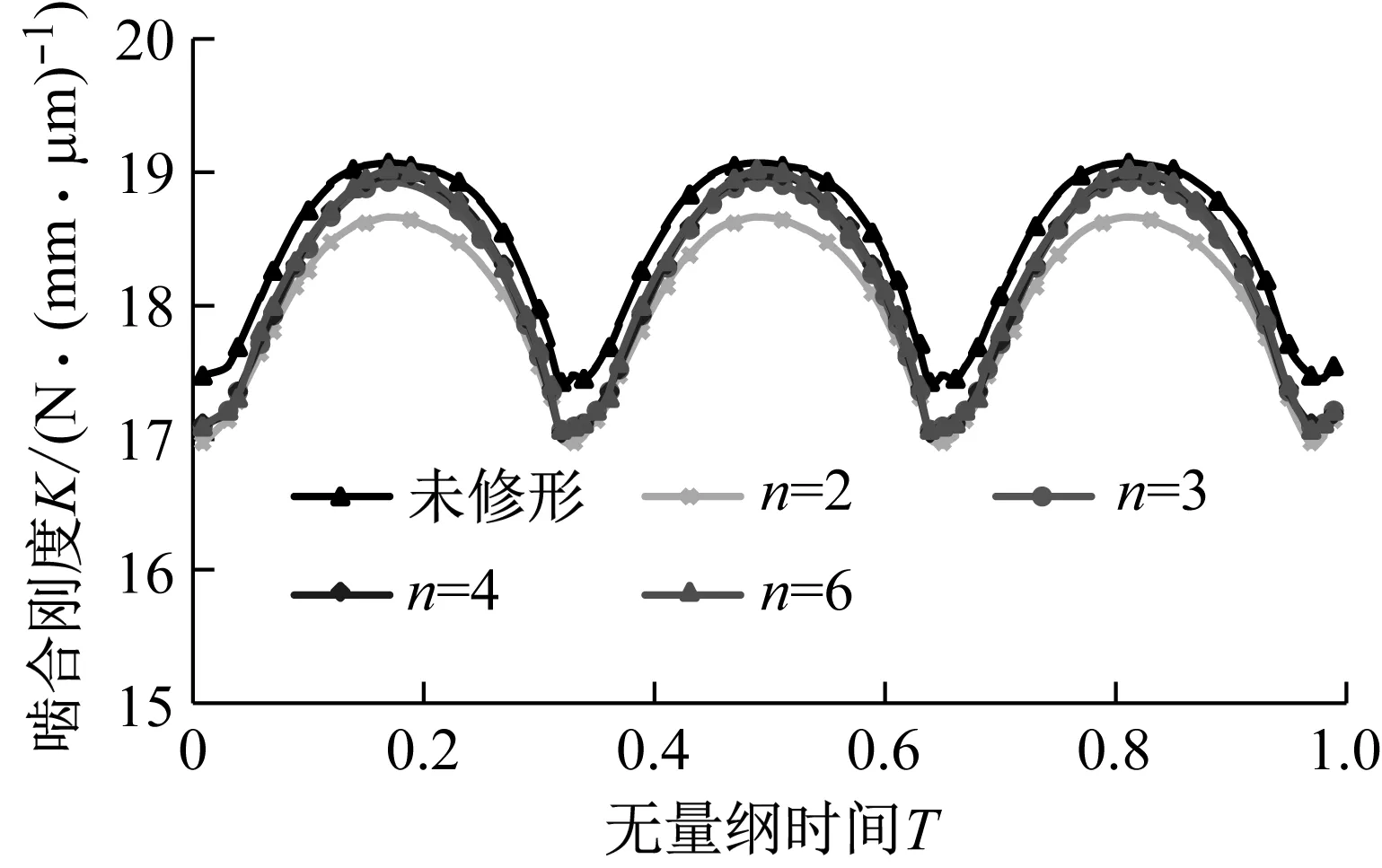
图14 不同修形曲线阶次时人字齿轮副的啮合刚度Fig.14 Mesh stiffness of double helical gears with different profile modification curve

4.5 输入转矩

其他参数保持不变，选取输入转矩变化范围为250～875 N·m，计算可得不同输入转矩下人字齿轮副的重合度和啮合刚度变化规律如表6和图15所示。随着输入转矩的增加，轮齿受载变形增大，齿廓修形区参与啮合的区域增大，齿轮副的重合度随之增加，轮齿接触线长度变长，时变啮合刚度均值增大，啮合刚度波动值随之变化。当输入转矩为500 N·m时，齿轮副重合度接近整数3，啮合刚度波动值较大；当输入转矩较小时，轮齿修形量偏大，齿轮副端面重合度小于1，可能引起啮合冲击，降低传动的平稳性。当输入转矩大于750 N·m时，啮合轮齿接触变形较大，齿廓修形区几乎完全进入啮合，齿轮副重合度不再变化，人字齿轮副啮合刚度不再受输入转矩影响。

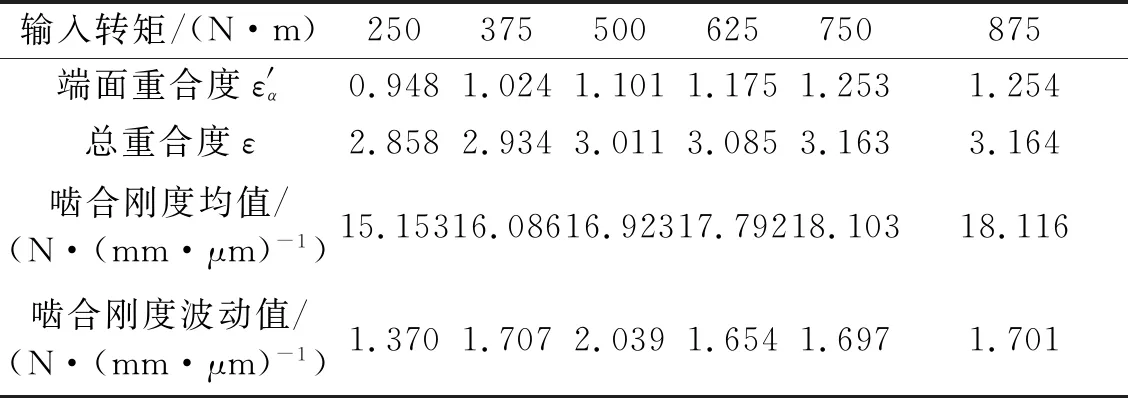
表6 不同输入转矩下人字齿轮副的重合度及啮合刚度Tab.6 Contact ratio and mesh stiffness of double helical gears under different input torque

图15 不同输入转矩下人字齿轮副的啮合刚度Fig.15 Mesh stiffness of double helical gears under different input torque

5 结 论

(1) 考虑轮齿修形和受载变形对齿轮副重合度和啮合状态的影响，提出了一种计入齿廓修形参数和退刀槽宽度的人字齿轮啮合刚度计算方法，与有限元法计算结果对比分析，验证了解析算法的正确性。

(2) 齿廓修形后，齿顶和齿根修形区齿厚减薄，轮齿刚度减弱，受载时人字齿轮部分修形区参与啮合，端面重合度减小，修形齿轮啮合刚度较未修形齿轮有所减小。

(3) 人字齿轮副退刀槽宽度增大，啮合刚度均值增大，啮合刚度波动值变化不大；修形人字齿轮副的重合度及啮合刚度均值随修形量、修形长度的增加而减小，随修形曲线阶次的增加而增大，输入转矩增大时，啮合刚度均值先增大而后不再变化；修形量、修形长度和输入转矩对齿轮啮合刚度波动值有较大影响，当总重合度接近整数时，啮合刚度波动值较大。