GeoGebra 软件在数学分析教学中的应用举例

闫永芳

(晋中师范高等专科学校,晋中 030600)

随着互联网信息化的发展和应用,整个世界、整个社会都在悄悄地发生着巨大的变化,传统的教学方式和教学内容已经难以满足新时期大学生的需求。 特别是各类教学软件的出现,给课堂教学带来了很多方便,给学生带来更多自主学习的机会与更多的学习内容,同时也给教师提出了更高的要求。 各类教学平台的出现,给学生提供了更多的选择机会与更多学习的机会,同时也给教师带来了更多竞争对手。 作为新时期的教师,要接受各类不同的教学软件给自己带来的便利,要接受各类不同的教育平台给自己提出的更高的要求,同时也要驾驭互联网信息化时代给予的各类挑战。 时代在发展,学校也在发生着翻天覆地的变化,以前需要多媒体教室要提前申请、排队等待,现在每个学校几乎每个教室都装有多媒体,从小学到大学无一例外,这就要求每个教师都要会使用多媒体教学,要会使用现代化软件备课,会利用教学平台给学生授课。

作为高校数学教师,各类数学软件给我们带来了很多方便。 数学离不开图形,数形结合能够解决很多数学问题,对于数学教育专业的学生而言,数学分析中的问题经常很抽象,有些复杂的函数难以想象出图象是什么样子的,而用GeoGebra 软件能帮助学生的解决这样的问题。 用GeoGebra 软件做数学图形不仅形象而且直观,还能在教学过程中显示同类函数变化时图形的变化过程,让同学们在学习的过程中随着图形的变化掌握函数的性质,从而解决函数中遇到的各类不同的问题。 GeoGebra 软件不仅有电脑版还有手机版,同学们遇到问题可以随时随地用手机版GeoGebra 软件作图解决。 Geo-Gebra 软件在数学分析教学和学习中起着很重要的作用。

在上数学分析课程时同学们经常会遇到如下问题:对初等函数的性质没有完全掌握,对初等函数中随着自变量的变化函数如何变化分析不清楚;当初等函数系数变化时函数图象又如何变化有混乱;求函数凸凹性拐点、描绘函数图象时搞不清楚函数走向、三角函数反函数的图象画不出来;不能理解为什么无限接近怎么不相交等问题。 借助于GeoGebra 软件辅助数学专业的学生学习会起到意想不到的效果,下面举例介绍GeoGebra 软件在高校数学教育专业教学中的应用。

一、GeoGebra 软件在“反三角函数”教学中的应用

高中课改后,高中数学主要学习正弦函数、余弦函数、正切函数三个三角函数,但是考入数学教育专业的学生在微积分中会经常遇到余切函数、正割函数、余割函数三个三角函数,也会经常遇到正弦函数、余弦函数、切函数和余切函数的反函数。我们在教学过程中首先要把这些空缺补上,学习反函数要和原函数对应起来,不然三角函数反函数的性质很难掌握。 下面我们用原函数的定义域是它的反函数的值域作三角函数和对应的反三角函数在同一坐标系中的图象来看反三角函数的性质。

(一)正弦函数y=sinx 和反正弦函数y=arcsinx

由于反函数的函数的性质,函数必须是单调的,那么我们取正弦函数y=sinx离坐标原点最近的(- π/2,π/2)这个单调区间,它的反函数写作y=arcsinx(-1,1),读作反正弦函数。 根据互为反函数的两函数的关系,我们知道函数y=sinx的定义域是它的反函数y=arcsinx的值域,函数y=sinx的值域是它的反函数y=arcsinx的定义域。 它们的图象关于y=x对称,同是增函数(或同是减函数)。知道这些性质后,我们能想象反正弦函数的图象,但是我们的学生很难画出来,那么我们用GeoGebra 软件输入y=arcsinx,函数会出现,学生也会恍然大悟。 我们再在同一坐标系中画出y=sinx的图象(如图1)。 根据互为反函数的两个函数的性质比较,同学们会对反正弦函数有更新的认识,并且能够记在自己的头脑中。

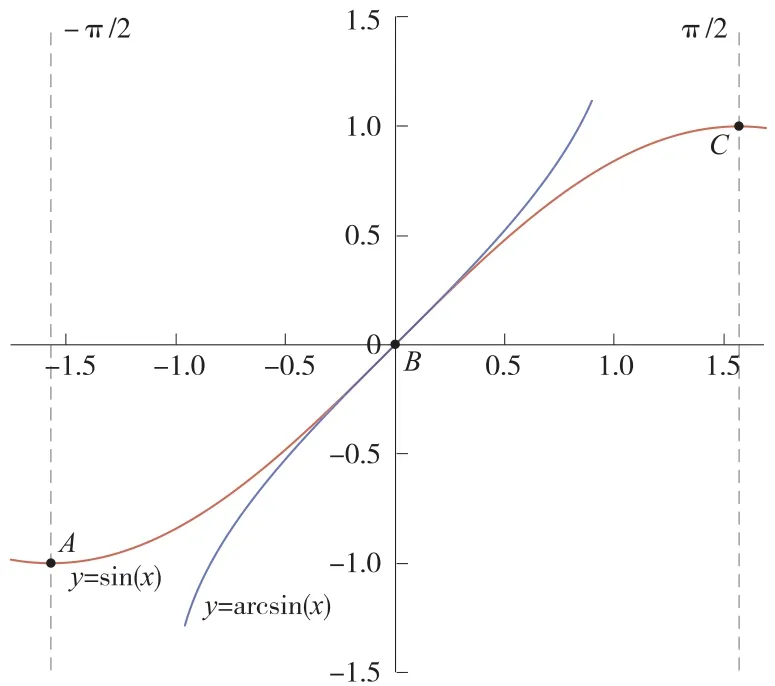
图1

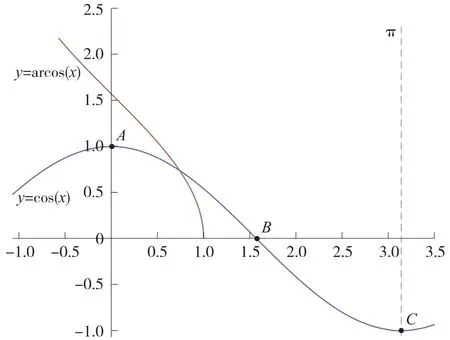
图2

(二)余弦函数y=cosx 和反余弦函数y=arccosx

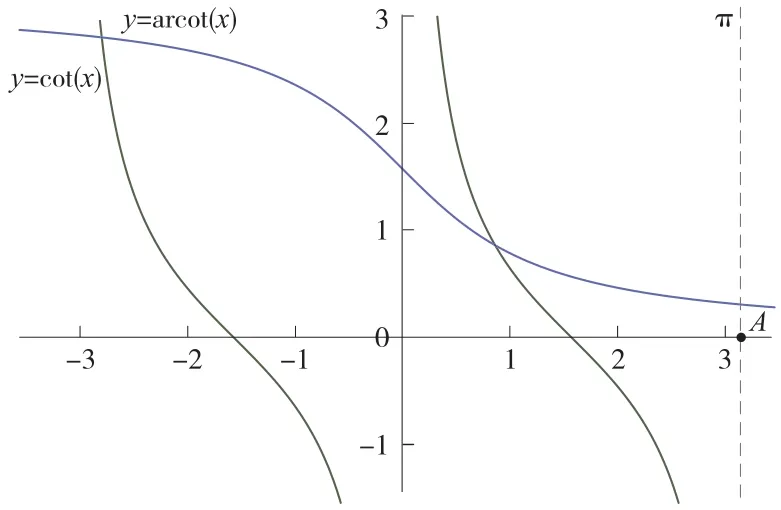
图3

同理,我们取余弦函数y=cosx离坐标原点最近的(0,π)这个单调区间,它的反函数写作y=arccosx(-1,1),读作反余弦函数。 用GeoGebra 软件做出图象(如图2),根据图象我们来学习反余弦函数的性质。

(三)正切函数y=tanx 和反正切函数y=arctanx

取正切函数y=tanx在坐标轴附近的一个单调区间(- π/2,π/2),它的反三角函数写作y=arctanx(-∞,+∞),读作反正切函数。 用GeoGebra软件做出图象(如图3),根据图象我们来学习反正切函数的性质。

(四)余切函数y=cotx 和反余切函数y=arccotx

取余切函数y=cotx在坐标轴附近的一个单调区间(0,π),它的反三角函数写作y=arccotx(-∞,+∞),读作反余切函数。 用GeoGebra 软件做出图象(如图4),根据图象我们来学习反余切函数的性质。

图4

同理,我们可以用GeoGebra 软件做出另外两个三角函数及它们的反三角函数的图象,再按照图象分析、学习它们的性质。 在利用GeoGebra 软件做出的图象时,要注意讲清楚在定义域范围内取函数图象,不在定义域范围内的图象,自己作图时要舍弃。 结合GeoGebra 软件图象同学们能很快做出理想的函数或反函数的图象,很好地理解和掌握反三角函数的图形和性质。 这样学习不会使同学们感觉枯燥,如果忘记图象,还可以用手机版的Geo-Gebra 软件画出图象,随时随地学习。

二、GeoGebra 软件在“导数在研究函数上的应用”教学中的应用

利用导数我们可以求函数的单调性及单调区间、求函数的极值与最值、求函数的凹凸性,结合函数的渐近线,进而描绘函数的图象。 例如,讨论函数y=e-xsinx的凸凹性和拐点,并描绘出函数的图象。 按照步骤来分析:

1.函数y=e-xsinx的定义域是R;

2.函数y=e-xsinx不是奇函数,也不是偶函数,也不是周期函数,没有渐进线;

3.分别求出函数y=e-xsinx的一阶导数和二阶导数。y′=e-x(cosx-sinx),y〞=-2e-xcosx,确定单调区间、极值、凹凸性、拐点,令一阶导数y′=0,解得x=kπ+π/4(k∈Z),用他们可求出函数的极值点,令二阶导数y〞=0,解得x=kπ+π/2(k∈Z),将R分为无穷个区间:…(-3π/2,-π/2),(-π/2,π/2),(π/2, 3π/2),…;

4.列表见表1、表2;

表1 凸凹区间和拐点表

表2 增减区间和极值点表

根据表格可以找到极值点、拐点、增区间、减区间,大致画出函数的图象,但是图象复杂,很多同学还是不能准确画出,所以可以用GeoGebra 软件,直接输入函数得到图象(如图5),然后对比自己找出的关键点和图象,放大y轴,确定自己做出的图象是否正确。

图5

三、GeoGebra 软件在“多元函数微分学”教学中的应用

我们在学习多元函数微分学时经常会遇见这样的问题,如描绘平面区域的图象、描绘空间区域的图象等。 对于平面区域图象,我们能够想到,但是空间区域就没那么好想了,如函数z=1-x2-y2(如图6),z=xy(如图7)(如图8)等,看似是我们常用的函数,但做它们的图象也是很不容易的,而借助GeoGebra 软件,这些函数的图象就很容易画出来了,然后根据软件做出的图象,自己再做就容易多了。

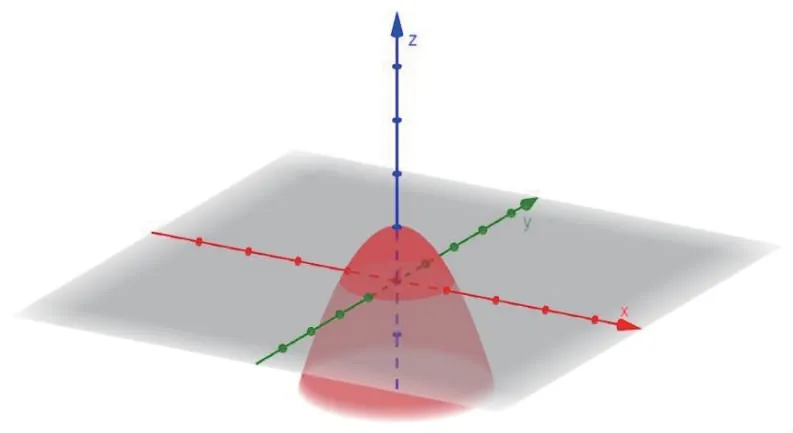
图6

GeoGebra 软件在数学分析中的求极限、函数的连续性、导数、不定积分、定积分、求面积等教学中也起到了很重要的作用,不仅有助于教师教学,更有助于学生学习,还能在课后起到很好的辅助作用。 学生在学习过程中,可以利用GeoGebra 软件作图辅助理解;学生在做作业时做不出图象的,可以通过GeoGebra 软件做出图象,便于去理解、体会;教师经常用GeoGebra 软件辅助教学,使同学们不会再觉得数学课堂枯燥无味;学生经常用GeoGebra 软件辅助学习,不仅能解决数学问题,还能提高学习数学的积极性。

图7

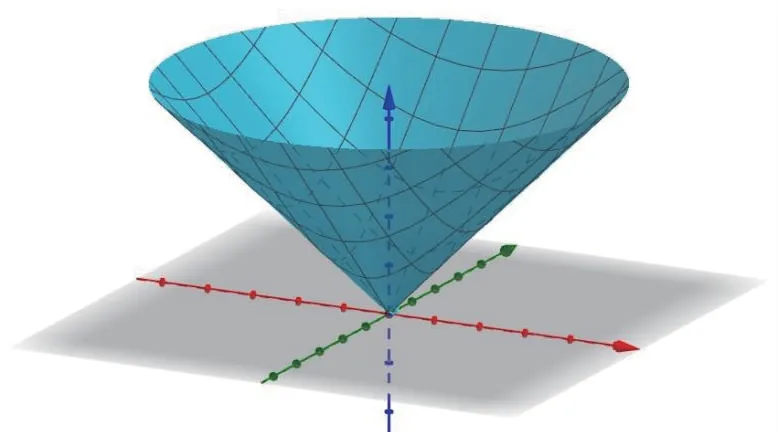
图8

总之,GeoGebra 软件在数学分析教学中能起到很好的辅助作用。 数学离不开图形,有了Geo-Gebra 软件辅助作图,凡是数学中由于图形引起的难解之题,都会迎刃而解;凡是图象和性质之类难理解的问题,也都不费吹灰之力就能掌握。 在教学和学习中,我们能积极地应用GeoGebra 软件,提高学生学习数学的兴趣,从而使学生对数学产生兴趣,那么我们的数学课堂也会趣味无穷。