2005—2020 年深圳市淋病疫情时间序列分析

翁榕星 张春来 文立章 叶健滨 王洪琳 洪福昌 陈祥生 蔡于茂

1 深圳市慢性病防治中心，广东深圳518020； 2 中国医学科学院皮肤病研究所 中国疾病预防控制中心性病控制中心，南京210042

淋病是由淋病奈瑟球菌所致的常见性传播疾病。据WHO 估计，2016 年全球约有8 600 万新发淋病感染患者[1]。 在中国，淋病是乙类法定报告传染病，每年报告约115 000 例新病例[2]。 由于目前缺乏针对淋病的可用疫苗以及耐药菌株的持续出现，因此监测和预测淋病的流行状况和趋势对其防控十分重要。2014 年深圳报告淋病发病率为53.01/10万，居全省首位，远高于全国水平[3]，表明淋病仍然是深圳的主要公共卫生问题。本研究基于深圳市2005—2020 年的淋病监测数据， 构建自回归移动平均（ARIMA）模型来预测深圳淋病发病率的时间趋势，对淋病流行趋势进行预警，为深圳的淋病防控工作提供参考依据。

资料与方法

2005—2020 年深圳市淋病的发病率趋势如图1 A 所示， 呈现明显的周期波动规律， 每年于1—2月处于流行低谷，于7 月及10 月到达流行高峰。 总体趋势而言， 深圳市淋病发病率从2014 年开始呈明显上升趋势，于2017 年达到顶峰，随后开始逐步下降（图1 B），并且深圳市淋病发病率有着以年为单位的周期性波动（图1 C）。在时间序列去除趋势、季节性后的偶然性波动为随机波动，受偶然性因素影响（图1 D）。

一、资料来源

收集中国疾病预防控制信息系统里2005 年1月至2020 年11 月年深圳市淋病月发病统计数据，人口资料来自深圳市统计年鉴。

二、分析方法

1. 数据集的建立和模型介绍

将序列分为训练集和验证集， 其中2005 年1月—2020 年5 月作为训练集用作模型建立，2020年6—11 月作为验证集用作模型评估。应用软件R 3.5.0 版本建立ARIMA 模型。ARIMA 模型的表现形式一般为ARIMA （p，d，q）×（P，D，Q）s， 其中p 和P分别为非季节性和季节性自回归阶数，q 和Q 为非季节性和季节性移动平均阶数，d 和D 为非季节性和季节性差分次数，s 为季节周期[4]。

2. 模型的识别

在建立模型前， 需要观察并应用Augmented Dickey-Fuller（ADF） 检验来检测时间序列的平稳性，对不稳定的序列做差分处理[5]。 待序列平稳后，观察其自相关图（ACF）和偏自相关图（PACF）的拖尾或截尾状况来识别模型的参数。 根据参数构建一个或数个模型，对比BIC 值选择拟合最优的模型。

3. 模型的参数检验、诊断和评价

用最小二乘法计算最优模型的参数，再对模型的残差序列进行Ljung-Box 检验， 以检测其是否为白噪声序列， 并用QQ 图检测残差是否服从正态分布[6-7]。 通过上述检测后，模型应用于验证集，以平均绝对百分误差（MAPE）为评价标准，MAPE 值在5%～10%认为模型高度准确，10%～20%认为模型是好的，20%～50%认为模型是合理的，＞50%认为模型不准确[8]。

结 果

一、深圳市淋病的发病率趋势分析

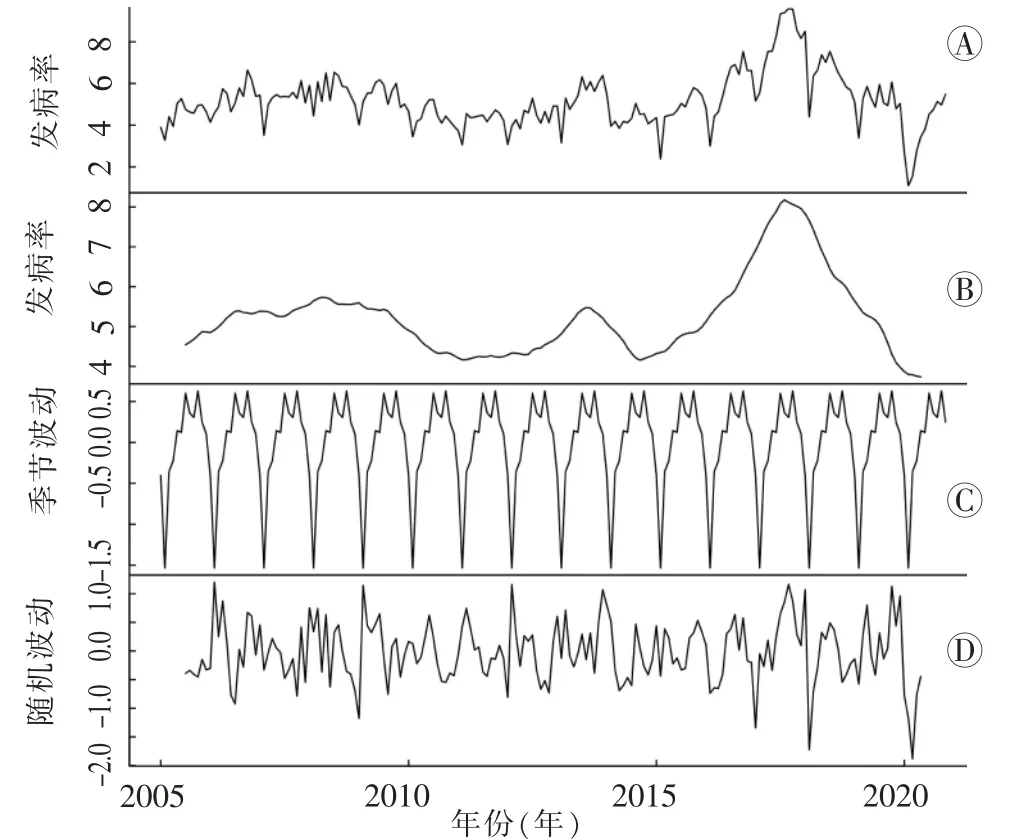
图1 2005—2020 年深圳市淋病发病率时间序列分解示意图

二、模型的识别及选择

ADF 检验结果表明，2005 年1 月—2020 年5月深圳市淋病发病率的时间序列不稳定，因此需要进行平稳化处理。 经一阶普通差分及一阶季节性差分后（图2 A），序列变化趋势消除，数值围绕0 值上下波动并通过了ADF 检验（P=0.01），序列趋于平稳。

序列平稳后可初步确认ARIMA （p，d，q）×（P，D，Q）s模型中，d=1，D=1，s=12。通过观察ACF 图（图2 B） 发现Lag=1、2 处超出95%CI，q 值在0、1 或2间选取；通过观察PACF 图（图2 C）发现Lag=1、5、8处超出95%CI，p 值在0、1、5 或8 之间选取。 关于P和Q 的取值的选取， 一般不超过2 阶， 通过观察ACF 图发现Lag=12 处超出95%CI，Q=0 或1； 观察PACF 图发现Lag=12、24 处超出95%CI，P 值在0、1或2 之间选取。比较模型间的BIC 值，BIC 最小的模型为最优模型。

图2 淋病发病率差分处理后示意图

三、模型诊断和参数检验

最终确定BIC 最小的模型为ARIMA （0，1，1）（2，1，1）12模型（BIC=370.51）。 在模型标准化的残差图中， 残差以平均值为0、 恒定的方差进行分布。ACF 图显示自相关系数大部分在95%CI 内，Ljung-Box 检测P 均＞0.05，表明该模型的残差序列为白噪声序列。 QQ 图检测显示该残差序列服从正态分布。模 型 的 参 数 检 验 如 表1 所 示，ARIMA （0，1，1）（2，1，1）12模型的参数检验均有统计学意义。 因此，该模型可以用于验证集预测2020 年6—11 月深圳市淋病发病率。

四、模型预测

将ARIMA （0，1，1）（2，1，1）12模型应用于预测2020 年6—11 月深圳市淋病发病率， 如图3 所示，2020 年6—11 月的真实值均在预测值的95%CI内。该模型预测水平较优，MAPE 值为18.35%。该模型预测结果显示2021 年深圳淋病发病率将继续下降，区间为0.68/10 万～3.70/10 万。

表1 ARIMA （0，1，1）（2，1，1）12 模型参数检验结果

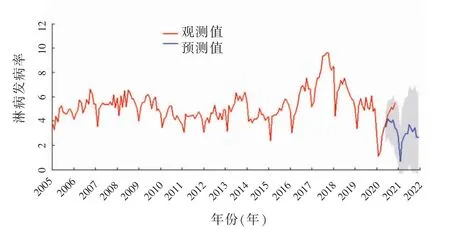
图3 2005—2020 年深圳市淋病发病率趋势及预测结果图

讨 论

传染病流行趋势的预测对疾病防控有着重要指导作用，当前许多有用的数学和统计方法被广泛应用于传染病预测领域。 时间序列分析即通过应用时间变量有效预测传染病的未来发病率和流行病学趋势。 在多种预测技术中，ARIMA 模型已经越来越受到青睐，并成功应用于登革热、结核病和腮腺炎等传染病预测中[9-10]。 ARIMA 模型具有短期预测准确性高且易于实施的优点[4]，经济且高效的特点也可应用于经济不发达的地区，并及时提供干预手段。本研究应用ARIMA （0，1，1）（2，1，1）12模型来预测2020 年6—11 月深圳市淋病发病率， 发现有着周期性波动以及继续下降的趋势，与实际发病率趋势基本一致，预测结果较好，表明该模型可很好地拟合周期性波动和长期趋势， 因此ARIMA 模型能够应用于淋病发病趋势的预测。 另外， 模型预测2021 年深圳淋病发病率将维持在一个较低水平，这可能与目前政府采取相关防控措施，就诊人群可能因减少接触等原因减少就诊，但不排除后期随着人员流动性增加， 相应的淋病发病率可能会随之变化，因此模型需要及时更新。

本研究还发现2005—2020 年深圳市淋病发病率存在明显的周期性波动， 从每年的12 月到次年的2 月有所下降，并在次年的2 月进入低谷，随后又逐渐上升，该结果与梅毒的发病率季节波动相似[11]，这个现象可解释为“春节效应”[12]，即春节期间新发感染人数下降，春节后回升，该效应一般由大量外来人口在春节回乡导致，该人群更有可能发生高危性行为，因此更容易感染性病[12]。 此外，“春节效应”可能造成患者淋病治疗的推迟，还可能将感染进一步传播给他们的性伴侣[13]。因此，需对外来劳务工作为重点的干预对象，降低高危性行为的发生。

本研究中亦存在一些局限性。 在拟合ARIMA模型之前，必须保持时间序列平稳。其次，ARIMA 模型都只能应用于短期预测，随着时间的推移，应不断添加新的观测序列以调整模型， 确保预测准确性。 此外，该模型的精度还受到监测数据质量的影响，迟报、漏报以及重复报告均可影响数据的质量。由于深圳市性病疫情报告网络较健全，市、区级慢性病防治机构定期开展相关培训以及性病疫情督导工作，各级医疗机构严格按要求进行性病报告工作，大大减少了迟报、漏报以及重复报告的情况发生[14]，因此该模型能相对准确地反映深圳市淋病发病率趋势，并应用于未来的预测工作中。

利益冲突 所有作者均声明不存在利益冲突