大侧斜桨非定常空化流动结构的数值研究

韩承灶，龙 云，季 斌

（武汉大学水资源与水电工程科学国家重点实验室，湖北省武汉市 430072）

0 引言

随着舰船逐渐向着高航速、大型化发展，螺旋桨作为现代舰船应用范围最为广泛的推进器之一，其空化性能对于航行器的快速性、隐蔽性和安全性的影响不可忽视，同时对于船体减振降噪的要求越来越高，因此必须对船尾非均匀来流下螺旋桨空化以及空化对桨叶周围流动结构的影响情况开展数值模拟研究，掌握其空化演变规律和内部流动情况[1-2]，从而为控制其影响提供指导。

目前国内外对于船舶螺旋桨空化流动问题的研究主要采用试验研究和数值模拟两种手段。Alves-Pereira等人[3]基于试验的方法对螺旋桨叶片近区压力场变化与空化演变过程进行了定量分析。他们利用谐波分析和图像处理技术建立了压力脉动和空化形态之间的关系。Stella等人[4]基于LDV技术采用两种采样方法研究了螺旋桨周围的空化流动问题。并且这两种方法从准确性和效率的角度互为补充。Pecoraro等人[5]通过比较和研究了有无螺旋桨情况下船后的流动特性和分离机理，提出了一个可以准确地识别船尾分离流区的偏度系数。而随着计算机运行速度的逐步提高，CFD技术快速发展起来，在一定程度上弥补了试验过程资源耗费以及结果较为单一的缺点。Lindau等人[6]模拟了不同进速系数下的螺旋桨空化流动过程，验证了不同工况下螺旋桨推力和扭矩的故障。Lu等人[7]还基于同一非结构网格分析对比了URAN和LES方法的计算结果，但是研究计算中并未考虑实际过程中船后非均匀来流的影响。

本文以大侧斜螺旋桨（HSP）为研究对象，开展一种典型螺旋桨的非定常空化流动大涡模拟（LES）研究。Kurobe等人[8]基于SEIUN-MARU船开展并公开了关于这种桨叶的空化试验数据，包括非均匀进流速度分布及非定常空化演变图案，由此能够在保留船尾非均匀伴流场的同时，还可以将计算和研究重心转移到单独螺旋桨的非定常空化上，实现螺旋桨空化的LES模拟计算。本文基于螺旋桨转矩计算验证和确认研究的基础，对HSP桨开展细致的LES计算，并主要对螺旋桨空化相关的流动特性进行分析，为今后螺旋桨的优化设计提供理论基础。

1 计算模型与方法

1.1 计算域与计算方法

本文选取HSP型号螺旋桨作为研究对象，螺旋桨直径D=220mm，叶片数为Z=5，转速为n=1050r/min。考虑到入口采用非均匀进流，螺旋桨距离计算域入口距离过大会导致高速区和低速区混合流态发生变化，非均匀性降低；距离太小容易影响计算的收敛性，因而通过多次对比选择计算域进口距离桨盘面0.7D较为合理。计算域出口距离桨盘面6D，径向为螺旋桨直径的3倍（见图1）。

图1 计算域和网格分布情况Figure1 Computing domain and grid distribution

非均匀来流条件下的数值模拟，入口采用速度入口，通过求解器的profile功能来定义进口非均匀速度入口。出口采用压力出口，根据空化数的大小来定义出口压力。螺旋桨以及桨毂壁面均设置为无滑移壁面，静止域外壁面设置为自由滑移壁面。为保证计算的收敛性以及精度，首先利用k-ωSST湍流模型对定常流动进行计算，待计算收敛之后以定常结果为初场采用LES求解非定常流场，空化模型采用Zwart空化模型[9]。非定常内迭代残差收敛标准设置为10-4。

1.2 网格划分

表1 网格数量分布Table1 Information about the mesh distribution

2 结果与讨论

2.1 螺旋桨空化模拟与试验对比

图2显示的是HSP桨一个旋转周期内典型时刻的片空化模拟与试验对比情况。图中模拟空化由蒸汽体积分数αv=0.1的等值面表示，3个螺旋桨旋转角度表示螺旋桨旋转周期内的3个时刻，桨叶表面的黑色圆弧线条为各半径位置处桨叶切面轮廓线，模拟中两种螺旋桨选取了和试验一致的桨叶切面，即0.3、0.4、0.5、0.6、0.7、0.8、0.9和0.95R。为方便观察和对比，各个旋转角度的叶片均被人为旋转至0°位置（即桨叶旋转至正好螺旋桨参考线在12点钟方向）。网格1到3代表HSP桨网格数从密到疏的3套网格。

螺旋桨实际运行中，常位于船尾不均匀尾流中，本文的计算保留了螺旋桨进流不均匀分布的特征，因而能够在螺旋桨运行条件比较接近实际流场的前提下研究空化的非定常变化过程。当螺旋桨进入不均匀伴流区之后，轴向流速变小，导致攻角变大，螺旋桨吸力面容易出现空化现象。图2（a）中LES结果较好地再现了桨叶上的空化初生。随后从图2（b）到图2（c），桨叶上的片空化从导边向随边生长，面积增大，到图2（d）和图2（e）时空化覆盖位置逐渐移动到近叶梢区域。最后到图2（f）时，桨叶表面的片空化逐渐收缩至叶梢且部分被卷吸进梢涡中。HSP桨上片空化在初生之后很长一段时间内均局限于桨叶导边的狭长范围内，而且在图2（e）和图2（f）中可看到，桨叶上的梢涡空化很少。

图2 HSP桨一个旋转周期内典型时刻的空化模拟与试验对比（试验结果[8]）Figure 2 Comparison of the predicted and observed cavity patterns during a propeller rotation cycle for HSP（Experimental results[8]）

从图2可看出，随着螺旋桨的旋转，桨叶会周期性的进出非均匀伴流场，螺旋桨片空化呈现出周期性的演变过程，会经历初生、发展到消亡或被卷吸进梢涡空化中的发展过程。

图3给出了更多梢涡空化与试验的对比结果，图中模拟空化由蒸汽体积分数αv=0.1的等值面表示。由于桨叶上梢涡空化不明显，故图3只在图2的基础上给出了旋转角度80°时的结果，可以看到HSP桨叶上的梢涡空化仅会稀疏地出现在流场中，强度很弱，螺旋桨叶梢附近的梢涡空化已经出现断裂现象，而且片空化消失之后梢涡空化也几乎不再存在。

图3 HSP桨梢涡空化情况（试验结果[8]）Figure 3 Tip vortex cavitation for HSP（Experimental results[8]）

2.2 螺旋桨空化模拟的验证和确认研究

本节对HSP桨有针对性地分别生成了3套系统加密的网格，并进一步对HSP桨的空化LES不确定度进行计算。由于没有试验数据作为参照，故将LES不确定度表示成最密网格的百分比数据。

首先对桨叶空化发生时的水动力学性能做LES不确定度分析。由于模拟计算中采用的是等推力系数原则，所以仅选取时均扭矩系数计算其LES不确定度，结果如表2所示。可以看到HSP桨扭矩系数LES不确定度非常小。虽然预测难度非常大，但表2中扭矩系数LES不确定度结果表明本文计算有还是相对较高的精度。

为定量表征空化的模拟效果，进一步对桨叶时均空化体积进行LES不确定度计算，结果如表2所示。HSP桨叶空化体积LES不确定度结果比扭矩系数偏高，说明空化体积的预测比扭矩系数更难，但是相对于目前的空化模拟来说本文的不确定度相对改善很多，因此本文的空化模拟精度也较好。

表2 LES不确定度Table 2 LES uncertainty

2.3 空化对桨叶周围流动结构影响

本节基于非定常计算结果，对HSP这种典型桨叶进行空化流动结构分析，并依据上述结果主要采用HSP桨的第二套网格（网格2）为例展开，以获得更多对螺旋桨空化流动特性的认识和理解。

为方便结果分析，本节会针对HSP桨分别选取几个典型时刻的结果，具体结果如图4～图6所示，结果中涉及的平面为对应位置的桨叶上的切片，且结果中的速度矢量均只表示当地方向，而与大小无关。

图4为HSP桨10°～50°时的空化结果，为方便结果分析，桨叶表示为黑色。图中空化由蒸汽体积分数αv=0.1的等值面表示，并对其进行透明化处理，因此如图中所示可以清晰看到空化脱离桨叶表面的分界线。以图4中的两个典型时刻为例，进一步处理出图5和图6中的结果。图5（a）中白色区域代表桨叶表面的片空化区，桨叶上的黑白相交处即为图4中的片空化脱离桨叶壁面交界线，空化下方的白色虚线代表的是图5中的空化尾缘线，图5（b）和图5（c）分别为图5（a）中显示的主流导边和叶顶梢涡区域的叶片切面。图6中的结果与图5的表示方法类似。

如图6所示，虽然HSP桨表面的空化会被回射流抬升而离开壁面，但HSP桨在经过尾流高伴流区的整个过程中流动均较为缓和，未观察到明显的流动分离。从图1的-10°表面空化初生到图4的10°位置，HSP桨上的空化发展较慢，直到30°和50°时才有较大范围的空化出现，空化脱离壁面现象亦相对更缓和。

图4 HSP桨三个典型时刻空化分布Figure 4 Cavitation distribution for HSP in three typical moment

当桨叶进入尾流高伴流区时，此时攻角变大，在桨叶吸力面导边附近，会出现很狭长的空化区。如图5所示，当螺旋桨旋转到30°时，大量空化出现，但是此时桨叶导边及空化区的流动均附着于壁面，没有出现流动分离。回射流会作用在片空化尾缘，如图5（a）中红色箭头所示。使桨叶表面出现较少片空化脱离壁面的现象。但是此时的回射流和梢涡强度均较弱，作用区域也很小。

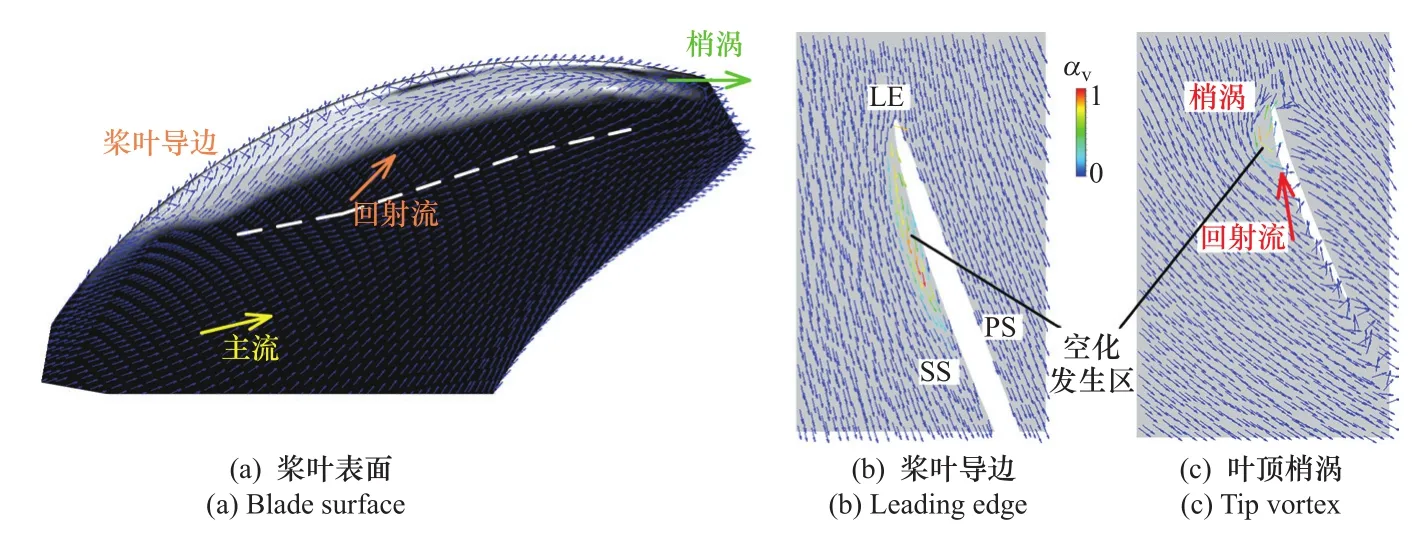
图5 HSP桨旋转角度30°的空化、涡结构和速度矢量分布Figure 5 Cavitation，vortex structure and velocity vector distribution around the HSP propeller at θ=30°

当空化逐渐向桨叶中部发展时，由于片空化前方存在较强的逆压梯度，回射流会形成并向片空化方向发展，从而进一步将片空化尾缘抬升并导致其脱离桨叶壁面，图5（a）中橙色箭头所示即为回射流的前进方向。随着流动进一步向随边方向发展，此时片空化已经消失，回射流亦不存在，桨叶表面主要为主流控制区域，其流动方向如图5（a）中黄色箭头所示。而在叶梢区域，片空化被回射流抬升，部分片空化依然附着于壁面，但是部分片空化已经完全脱离壁面，并被卷吸进梢涡中。图5（b）和图5（c）显示了桨叶导边流动、回射流和梢涡的具体流动情况。综上，如图5所示，此时桨叶表面空化区域主要有主流、回射流及梢涡等流动状态存在。

如图6（a）所示，当桨叶旋转到50°时，由于螺旋桨逐渐离开尾流高伴流区，攻角逐渐减小，桨叶主体部分流动均由主流控制，空化仅在叶片中上部及叶梢附近存在，如图6（b）所示，发生空化的桨叶导边附近流动均附着于壁面。桨叶空化主要集中在叶梢区域，回射流亦主要作用于此，大量的片空化被回射流抬升，如图6（c）所示。此时梢涡已经生成，虽然强度较低，但依然伴随着少量片空化被卷吸进梢涡中。此时桨叶表面空化区主要存在回射流与梢涡。

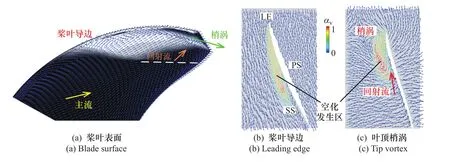
图 6 HSP桨旋转角度50°的空化、涡结构和速度矢量分布Figure 6 Cavitation，vortex structure and velocity vector distribution around the HSP propeller at θ=50°

2.4 螺旋桨空化与载荷分布

通过前文对螺旋桨空化、回射流和梢涡的分析，可以发现桨叶空化由导边发生后发展延伸到叶梢最终溃灭，其中梢涡空化演变强度较为微弱，而梢涡的发展与桨叶径向载荷变化密切相关，因此本节尝试对该桨发生空化时的载荷分布进行分析讨论。

本节整理出HSP桨叶各切面上提供的推力系数和扭矩系数随桨叶半径的变化关系，如图7所示。图中横坐标中r为各桨叶切面位置，R为桨叶半径，纵坐标中的KT和10KQ为各桨叶切面处提供的推力和扭矩分量，其沿横坐标积分即可得到该叶片总的推力和扭矩。可以看到，HSP桨靠近叶根附近提供的载荷较少，载荷的主要提供区域为桨叶中上部，其中桨叶载荷最重的区域位于0.8R的桨叶切面附近。靠近叶梢时，该桨上的载荷迅速降低，基本降到与叶根载荷同量级，起到了很好的卸载作用，因而梢涡强度很小。

图7 HSP桨载荷随半径变化Figure 7 Change of HSP propeller load with radius

3 结论

本文以HSP桨为研究对象，利用3套系统加密的网格，进行了螺旋桨非定常空化的LES计算，在螺旋桨空化LES验证和确认的基础上，对螺旋桨空化流动进行了细致深入的分析，并进一步探讨了两种桨叶空化对桨叶性能与流场的影响。本文的主要结论如下：

（1）从与试验对比的角度来看，LES预测的桨叶性能和空化结果具有较好的精度。计算结果很好地模拟出了HSP桨非定常空化的动态演变过程，空化会经历初生、发展、消亡或被卷吸进梢涡中的演变过程，而且较好地模拟出了桨叶梢涡空化的发展和断裂过程。

（2）将LES验证和确认方法用于分析螺旋桨空化模拟效果，得到了HSP桨叶空化发生时扭矩系数和时均空化体积的LES不确定度。结果表明，模拟得到的LES不确定度较小，表明通过本数值模拟获得的结果可靠性较高。

（3）通过分析螺旋桨旋转进入到离开尾流高伴流区的过程，细致研究了螺旋桨的空化流动过程，结果表明螺旋桨发生空化时，桨叶表面主要会有回射流、主流和梢涡等流动结构。HSP桨在经过伴流区的整个过程中，未发现有明显的导边分离流动，桨叶导边及空化区的流动均附着于壁面，片空化会出现在桨叶导边附近很狭长的范围内，回射流仅会小范围的出现，少量的片空化在叶梢附近被回射流抬升并被卷吸进入梢涡中。且桨叶表面空化流动平缓，叶梢卸载充分，梢涡和梢涡空化较弱。

（4）基于螺旋桨推力和转矩的变化分析了该桨发生空化时对于螺旋桨性能的影响情况。由结果表明，载荷由螺旋桨叶根到叶梢呈现先增大后急剧减小的趋势。螺旋桨重载区主要分布在桨叶0.8R左右，因此该桨叶空化收缩至叶梢区域时，叶稍卸载较好，因而梢涡空化强度较低。