课程思政背景下高等数学教学中体现哲学思想元素的探究与实践

张玉新，丁恒飞

数学是从现实世界中抽象出来的科学，它从数量关系和空间形式两个方面去研究现实问题.从某种意义上来讲，数学对所有学科的研究和发展都有一定的指导意义.数学和哲学很类似，具有超越具体学科和普遍适用的特点.因此，数学遵循哲学中辩证法的基本规律和观点.将哲学观点融入在数学教学过程中，既可以使学生在获取数学知识，同时也培养了他们的辩证唯物主义思想，进而提高了大学生的人文情怀［1-2］.然而，在高等数学的教学过程中，如何将具体的教学内容、所体现的思想和解决问题的基本方法同哲学中的基本观点结合起来，把辩证思想贯穿于数学教学的各个环节中，进而揭示出其所体现的哲学本质，这是每一位数学教师应当认真深思的问题.结合多年对高等数学的教学和思考，本文通过一些实例来说明高等数学中所体现的哲学思想，为进一步将课程思政融入数学教学过程提供帮助.

1 高等数学教学中体现的哲学规律

1.1 矛盾的对立与统一规律

矛盾存在于任何事物的内部，它的基本特点是双方相互依存，渗透和贯通，当具备了一定条件时，矛盾的双方可以相互转化，相互促进［3-4］.这种矛盾与转化的辩证思维贯穿在高等数学教学的始终，如果教师在教学过程中能充分挖掘出具有这种辩证思维的数学素材，就可以提高学生对概念的理解和记忆，进而提高教学效果，下面通过两个例子来说明这种思想和关系.

例1 微分和积分.假设F为函数f在区间I上的原函数，则他们之间具有如下关系.

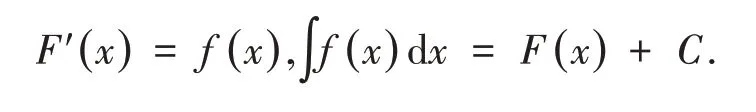
可见，求积分是求导数的逆运算，这说明它们之间是对立的.如果再进一步思考可以发现，基本的积分公式可以由基本求导公式出发推出，且它们两者组成了微积分的基本内容，这又说明它们之间是统一的.

例2 幂级数展开与级数求和.对常见的指数函数ex,有如下展开［5］.

特别地，取x= 1，进一步得到e= 1 + 1 ++ ….这说明一个无理数可以通过无穷多项的有理数去表示.此外，对于级数：利用函数的傅里叶级数展开式，可知其和为.这说明一些有理数的和等于一个无理数.由此可知，他们都是矛盾的双方，各自都以它的对立面的存在而存在.

1.2 矛盾的特殊性与普遍性规律

通常情况下，人们认识事物的根本方法是把矛盾的特殊性与普遍性辩证地统一起来，这是因为我们的认识总是从特殊推广到普遍，再用普遍去指导特殊［6-7］.在数学教学中，只有认识到一些概念的特殊性和普遍性，才能对概念有更深刻的认识.下面通过高等数学中的几个问题来了解这个观点.

例3 数列极限与函数极限.数列极限的概念是［5］：任给ε＞0，存在正整数N，当n＞N时，有|xn-a|＜ε.函数极限的概 念是［5］：任给ε＞0，存在X＞0，当 |x|＞X时，有 |f(x)-A|＜ε.从这两个概念可以看出，函数极限是对数列极限概念的进一步推广，而数列极限概念又是函数极限概念的特殊情形.在数学教学过程中，如果能将两者有机地结合起来分析和思考，会对它们有更深刻的认识.

例4 微分中值定理.从基本条件和表达式看，罗尔定理是中值定理中最简单的，因此，一般是先证明它，再由它推得拉格朗日中值定理和柯西中值定理，它们是罗尔定理的推广形式.但从另外一个角度来看，罗尔定理是拉格朗日中值定理的特例，而拉格朗日中值定理又是柯西中值定理的特例.下面可以通过图1 来清晰地看到它们之间的这种辩证关系［8］.

从以上的几个例子可以看出，如果把矛盾的特殊性与普遍性辩证统一地应用到一些数学概念的教学中，可以加深学生对概念的理解和记忆，起到事半功倍的效果.

1.3 运动和静止的辩证关系

世界上一切事物的存在和发展，都是绝对运动和相对静止的统一，它们之间是互相依存、渗透和统一的关系.高等数学中一些概念或者定理的产生，都是通过另外一些概念或者定理，将其中某些点或者线通过运动而产生，下面几个例子正好印证了这一辩证观点.

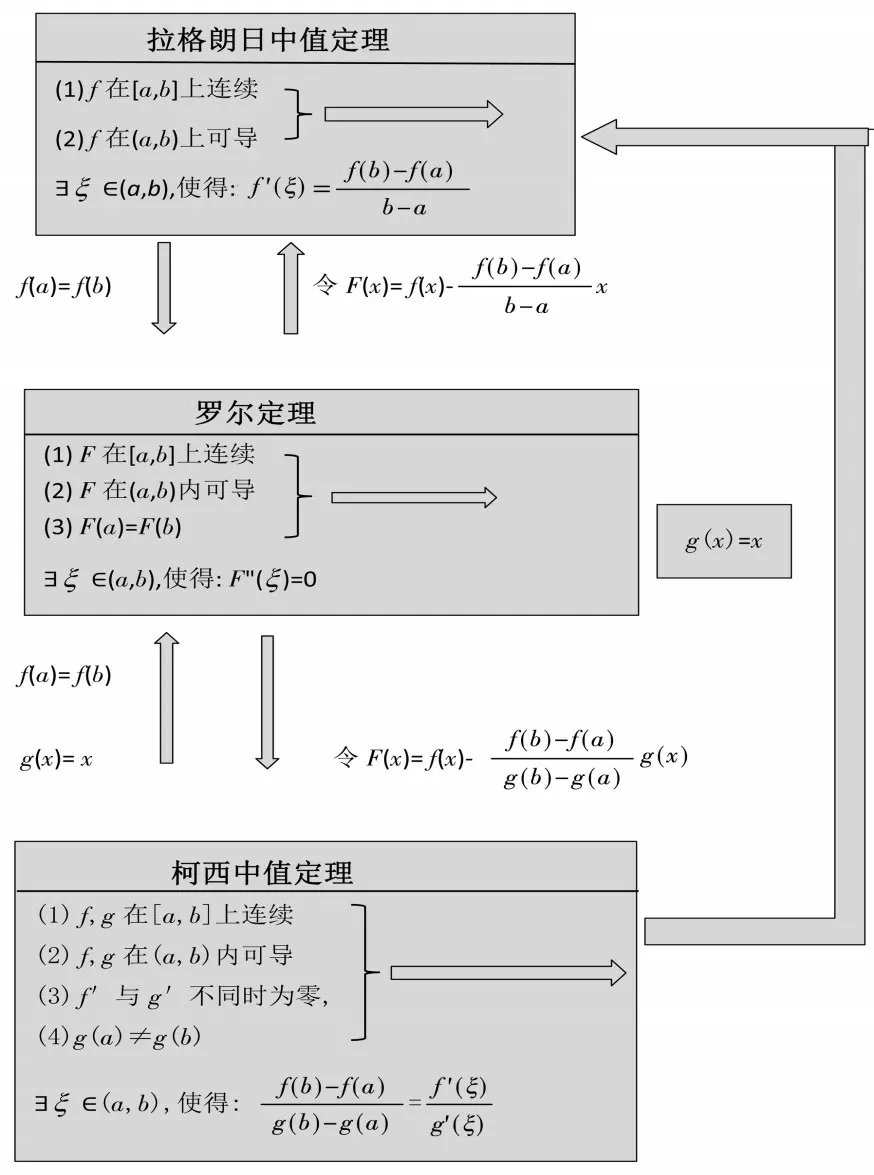
图1 中值定理之间关系图

例5 割线与切线的斜率问题.如图2 所表示，如果点M和N都静止，则我们可以得到割线MN的斜率为［9］：

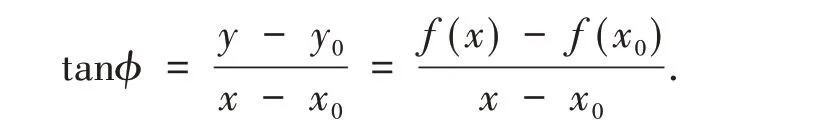
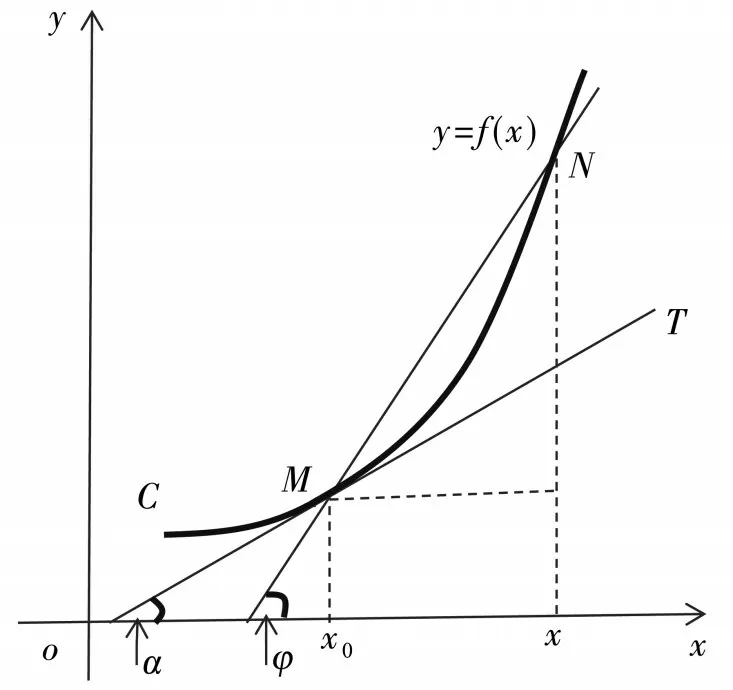
图2 曲线的斜率图

而当点M静止，而点N沿曲线C趋于点M时，我们可得切线MT的斜率为：

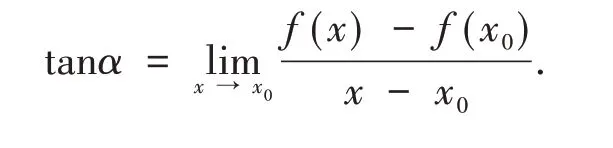
这就说明，这两个概念是相互依赖和相互渗透、彼此统一的.

例6 罗尔定理与拉格朗日中值定理的几何意义问题，如图3 所示.

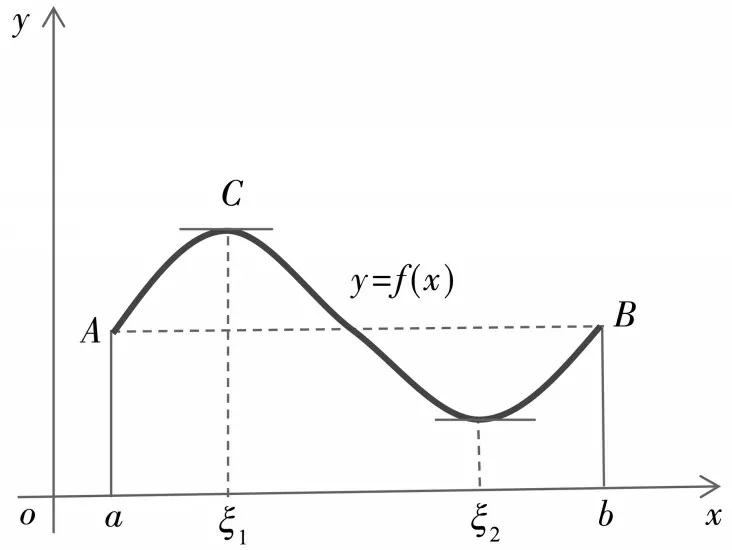
图3 拉格朗日中值定理图

罗尔定理的几何意义是［9］，若函数f(x)满足 条 件f(a)=f(b)，则 在 曲 线 弧 的 波 峰ξ1与波谷ξ2位置，曲线有水平切线，即满足f′(ξ1)=f′(ξ2)= 0.如 果 我们保 持A点不动，而将B点沿着平行于y轴的方向移动，所得结果如图4所示.

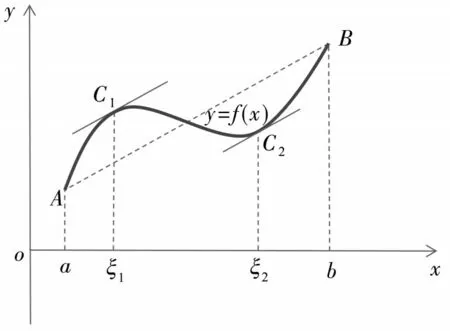
图4 柯西中值定理图

也就是说，若函数f(x)上除端点A和B之外其他点处具有不垂直于x轴的切线，那么这弧上存在某点，且该点处的切线平行于弦AB，这正是拉格朗日中值定理的几何意义.通过以上两个例子，可见运动和静止的辩证关系在高等数学中无处不在，如果能在教学中深刻挖掘且教会学生去辩证地看待这种关系，学生就能从已学的知识去探究一些更深层次的知识，对培养学生去积极探索未知的知识是大有裨益的.

1.4 量变与质变的辩证关系

质量互变规律是指量变会引起质变，质变又会引起新的量变，它们循环往复，交替进行［6-7］.高等数学中，有些量变达到一定程度之后，就会引起结果的本质变化，下面通过具体例子来体现这一观点.

例7 函数y=xn（n为自然数）的k阶导数问题.当k≤n时而当k＞n时这说明当阶数k超过临界值以后，结果恒为常数0，此结果一直持续下去.也就是说，量k达到一定程度后，引起结果变为0.

例8 函数的积分问题.考虑积分I1=根据高等数学知识，I1积分不存在，而对比这两个积分，可以发现被积函数完全相同，而只是将积分上限由1 变为∞，也就是说，量积累到一定程度，结果会发生了本质的变化.这两个例子很形象地说明了量变只有达到一定程度才会引起质变，如果在教学中注意到这一点，再结合课程思政的思想，可以让学生认识到：要想成功必须要坚持不懈，这对培养学生锲而不舍追求真理的精神是非常有益的素材.

1.5 整体与部分的辩证关系

整体与部分是辩证统一的，整体由部分组成，部分制约整体.因此，要厘清局部关系，用局部的发展推动整体的发展，再用整体的观点去指导局部［3-4］.高等数学课本中大量存在着这种整体与部分辩证关系的数学概念，如果用这种辩证的观点去理解，会起到意想不到的效果.下面通过两个例子来说明在教学中如何融入这种思想，去指导教学实践.

例9 极值与最值问题.极值是对某个邻域来讲的，它是一个局部概念，而最值针对的一般是整个定义域，它是全局概念.最值一般是不可导点、极值点和区间端点处函数值（如果能取到的话）中的最大值或最小值.

例10 函数的连续问题和一致连续问题.函数f(x)在区间I连续是指［5］，任给ε＞0，对任一点x∈I，都存在相应的正数δ=δ(ε,x)，只要x′∈I且|x-x′|＜δ，就有 |f(x)-f(x′)|＜ε.而函数f(x)在区间I上的一致连续是指，任给ε＞0，存在正数δ=δ(ε)，对任意的点x′,x′′∈I，只要 |x′-x′′|＜δ，就有 |f(x′)-f(x′′)|＜ε.可见，一致连续是整体性质，由它可以得到每一点都连续这一局部性质.也就是说，如果一个函数具有一致连续性则一定具有连续性，而函数具有连续性并不一定具有一致连续性.这两个例子说明任何事物都有其适应的范围，在教学中，可以通过这些例子来让学生认识到，做任何事情必须有“度”，这对培养学生的人生观和价值观是非常有意义的.

1.6 实践与认识的辩证思想

实践是认识的起点、基础、来源、动力和归宿.在高等数学的教学过程中，一定要深刻认识到实践的重要性，只有通过具体的实践，才能解决一些生产生活中的基本数学问题［3-4］.如果仅凭直观感觉，可能最后会得到错误的结果.下面，通过一道具体数学问题来说明实践对认识的指导作用.

例11［10］某一房地产公司有50 套公寓可供出租，如果将每月的租金定为180 元时，公寓将会没有剩余，但是如果将每月的租金增加10 元，公寓将会有一套剩余，且出租的房子每套每月需要维修费20 元，试问：要想获得最高收入，房租应定为多少元？

解 假设每套公寓出租费为x元/月，实际的收入就为( )x- 20 元/月，而出租的公寓数为因此，每个月总收入为：

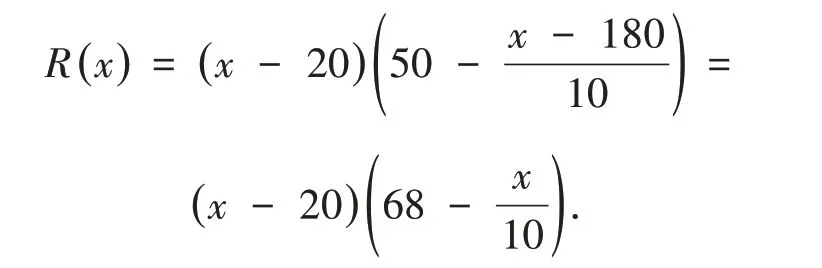
利用求导公式且令R′( )x= 0，可得唯一驻点x= 350，也就是说租金定为350 元/月时，利润最大，且为10 890 元.通过这个问题，说明只有通过具体的实践，也就是通过基本的数学理论和方法去计算，才能得到所求的正确结果，使学生认识到问题的本质，从而指导实践.

1.7 否定之否定规律

否定之否定规律，是事物不断完善和发展自己的一个有规律的过程，它表明事物经历了由肯定到否定，再到否定之否定的曲折发展过程［3］.高等数学中，好多问题不能用直接的办法解决，只得另辟蹊径，从它的对立面入手去寻找突破口，从而达到解决原问题的目的.

例12［10］证明f(x) =x3- 3x+a在［0，1］上不可能有两个零点.要解决此问题，直接办法不行，因此反设方程在此区间上有两个零点x1,x2，且设x1＜x2,即有f(x1) =f(x2).此时可知f(x)在［x1，x2］上满足罗尔定理，也就是说 存 在ξ∈(x1,x2)，使 得f′(ξ) = 0.注 意 到ξ∈(x1,x2) ⊂［0，1］，可得f′(ξ) = 3ξ2- 3 ＜0，两者矛盾，从而原结论成立.

例13［5］计 算(p＞0,b＞a).

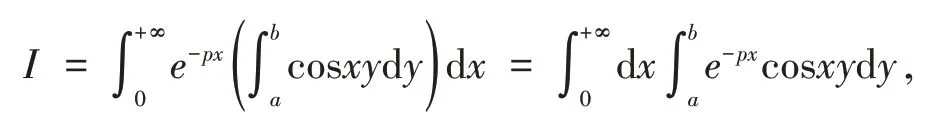
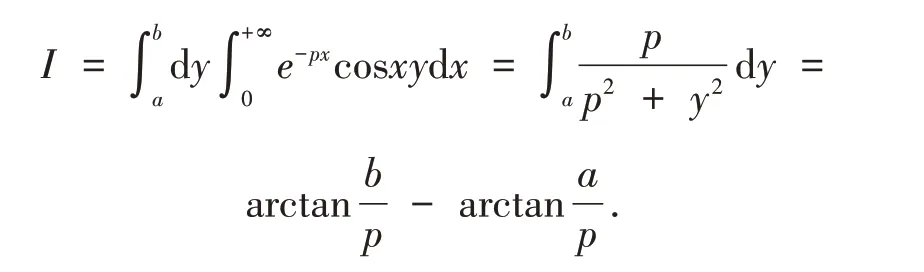
这样问题就迎刃而解了.

2 结语

文章通过日常教学中对高等数学教学内容的一些认识和实践，选取部分典型的实际例子来说明其所体现的哲学思想.从而发现如果能将这些哲学思想融入课堂教学中，可以提高学生的学习兴趣，对课堂教学效果是大有裨益的.事实上，高等数学体系庞大，内容繁多，大量概念蕴含着更深刻的哲学思想，因此，作为数学教师，一定要深刻挖掘数学概念和定理所包含的哲学思想，将其有效地融入到高等数学的教学过程中去.