千米级铁路悬索桥上无缝线路纵向力分布规律研究
2021-05-13张高祥曾志平
闫 斌,甘 睿,张高祥,曾志平
(1. 中南大学 土木工程学院,湖南 长沙 410075;2. 中铁二院重庆勘察设计研究院有限责任公司,重庆 400023)
目前,国内外学者已针对连续梁[1]、连续刚构桥[2]、钢桁拱桥[3]、连续梁系杆拱组合桥[4]、预应力混凝土独塔斜拉桥[5]、钢桁斜拉桥[6]等大跨度铁路桥梁与轨道相互作用问题开展了广泛而深入的研究,涉及梁轨非线性系统加载历史的模拟方法[5,7]、桥梁-轨道系统地震响应[8]、复杂轨道结构损伤[9]等,而针对大跨度悬索桥上无缝线路纵向力分布规律尚不明确。
为研究千米级悬索桥上无缝线路纵向力分布规律,建立了考虑主缆、吊杆、钢桁梁、正交异形板、钢轨,以及相邻桥跨结构的(84+84+1 092+84+84) m大跨度钢桁悬索桥与四线轨道相互作用仿真模型。研究了温度、竖向活载、列车制动作用下铁路悬索桥上无缝线路受力和变形规律。在此基础上,探讨了温度荷载模式等关键设计参数对系统受力的影响。
1 考虑钢轨伸缩调节器的桥上无缝线路仿真模型验证
采用非线性弹簧单元模拟线路纵向阻力,采用竖向刚臂模拟梁高,扣件竖向刚度由线性弹簧模拟[10],建立的有限元模型,见图1。
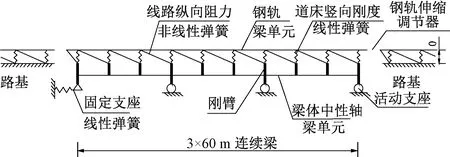
图1 梁轨相互作用计算模型
以该模型分析UIC 774-3—2001附录中C.5 连续梁桥算例[11],计算结果对比见表1。

表1 本文计算结果与UIC算例C.5计算结果对比
各计算结果与UIC算例均极为吻合,最大误差仅为0.77%,证明该模型可正确考虑钢轨伸缩调节器对梁轨相互作用的影响。
2 千米级铁路悬索桥工程概况
某公铁两用(84+84+1 092+84+84)m双塔连续钢桁梁地锚式悬索桥,上层设八车道高速公路,下层铺设双线客运专线和双线城际铁路,线间距为4.6 m。上桥面宽43 m,下桥面宽30 m,梁高16 m。其跨中截面形式见图2。
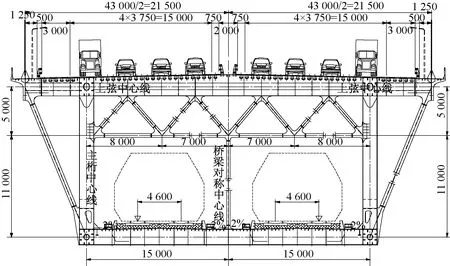
图2 悬索桥主梁截面(单位:mm)
悬索桥采用半漂浮结构体系。为提高悬索桥系统动力性能,在悬索桥桥塔与主梁之间设置有黏滞阻尼器。北塔塔高203 m,南塔塔高191 m,桥塔采用箱形截面,主缆边跨跨度350 m,见图3。
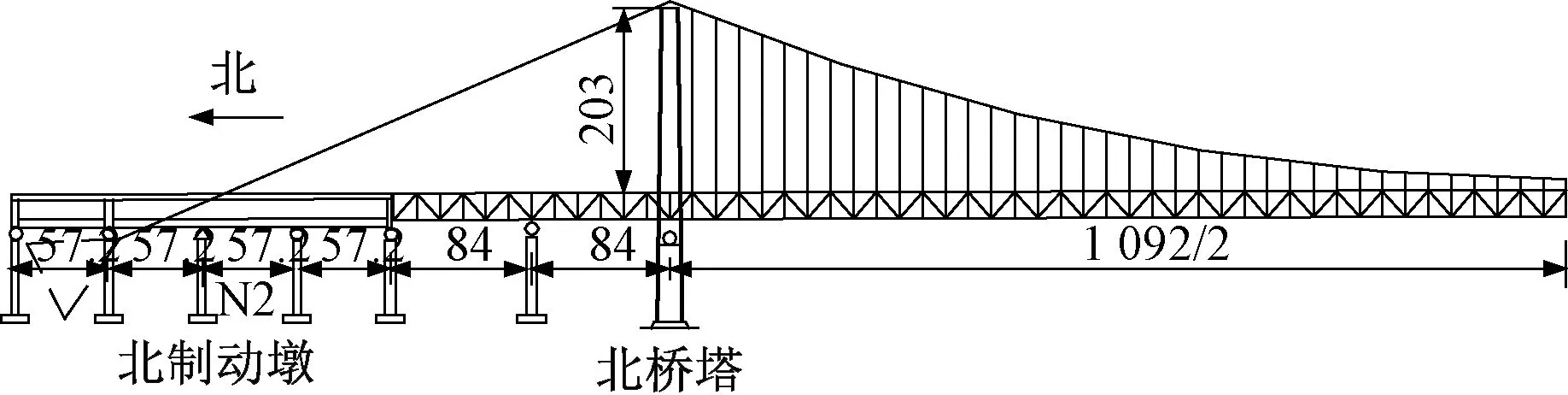
图3 悬索桥布置图(单位:m)
主缆矢跨比1/10,两主缆横向中心距为43 m。N2桥墩处为固定支座,其余桥墩处为活动支座。
悬索桥左右两侧分别设置4×57.2 m等截面预应力混凝土箱梁截面连续梁,连续梁跨中截面见图4。
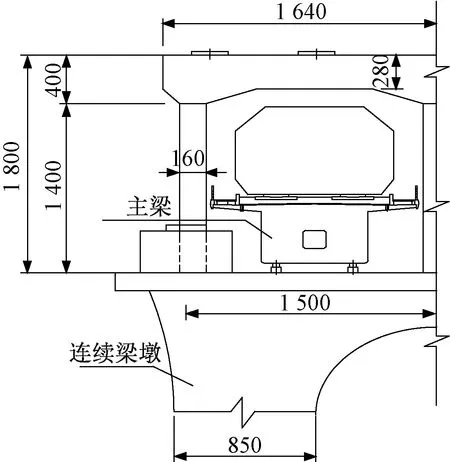
图4 连续梁梁截面(单位:cm)
3 大跨度悬索桥-轨相互作用仿真模型
桥塔底部采用6个等效刚度弹簧模拟群桩基础。相邻桥跨采用连续梁,中间桥墩处设固定支座,其余桥墩上设活动支座。主桁与桥塔横梁相交处只设竖向、横向约束,顺桥向无约束,活动支座仅约束竖向、横桥向位移[12]。
不考虑梁轨横向相对位移对轨道和桥梁纵向相互作用的影响,采用非线性杆单元模拟有砟轨道[13]。线路纵向阻力取值为

(1)
式中:r为线路纵向阻力,kN/m;u为钢轨-桥梁之间的相对纵向位移,mm。
采用线性弹簧模拟扣件竖向刚度[13]。 为减小边界效应,在路基段设置170 m路基上的钢轨[11]。悬索桥主梁为钢桁梁,钢桁梁是由不同截面类型杆单元组成。
假设桥塔顶端与主缆铰接,采用仅受拉的杆单元模拟主缆和吊杆主缆空间位置按照成桥线形考虑,主缆两端铰接在地基上,吊杆在悬索桥主缆和主梁上桥面处铰接[14]。
在计算温度荷载作用时,基于设计资料,当地最高轨温61.1 ℃,最低轨温-12.9 ℃,设计锁定轨温(30±5) ℃,此处将钢轨最大温降取为48 ℃,最大温升取为36.1 ℃。有砟轨道混凝土梁的温差取15 ℃,钢桁梁温差取25 ℃[13]。
在计算挠曲力时,客运线路采用ZK活载[13,15],城轨采用0.6UIC活载[11]。在计算制动力时,制动力率偏安全地取为0.25,加载工况见表2[16]。

表2 加载工况示意图
4 悬索桥上无缝线路设计方案
不设置钢轨伸缩调节器(以下简称“SJ”),考虑钢轨温降48 ℃,悬索桥温降25 ℃,相邻混凝土桥梁温降15 ℃[13],计算钢轨应力。不设SJ时,钢轨应力峰值出现在悬索桥两梁端附近,最高达218.0 MPa。为减小钢轨应力,在悬索桥两端设置SJ,计算其钢轨应力、钢轨纵向位移,见图5。
由图5可知,将钢轨伸缩调节器设置在悬索桥主梁两端处时,钢轨应力峰值在路基与连续梁交界处达181.0 MPa,钢轨纵向位移达44.3 mm,钢轨伸缩调节器伸缩量达69.8 mm。此时固定支座最大墩顶水平力降低至176.7 kN。将钢轨伸缩调节器设置在悬索桥主梁两端时能有效降低悬索桥梁端钢轨应力和制动墩墩顶水平力。
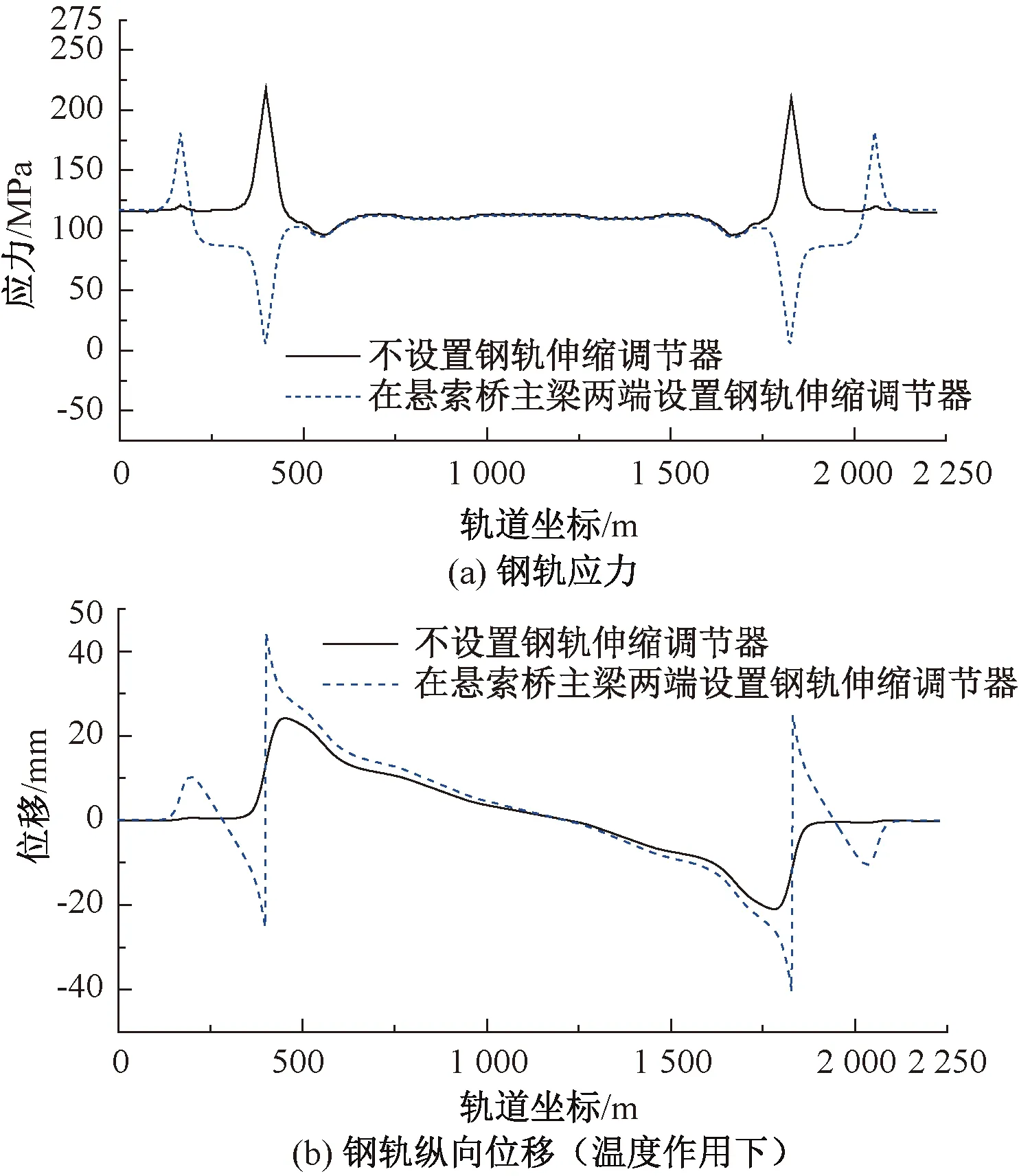
图5 SJ设置对系统受力和变形的影响
5 大跨度悬索桥上无缝线路纵向力分析
5.1 温度荷载作用
在悬索桥主梁两端安装SJ,设置四种工况,研究主梁、桥塔、主缆和吊杆等部件温度变化对系统受力和变形的影响:工况一为主梁温降25 ℃;工况二为桥塔温降15 ℃;工况三为主缆温降40 ℃;工况四为吊杆温降40 ℃。各工况计算结果见图6。
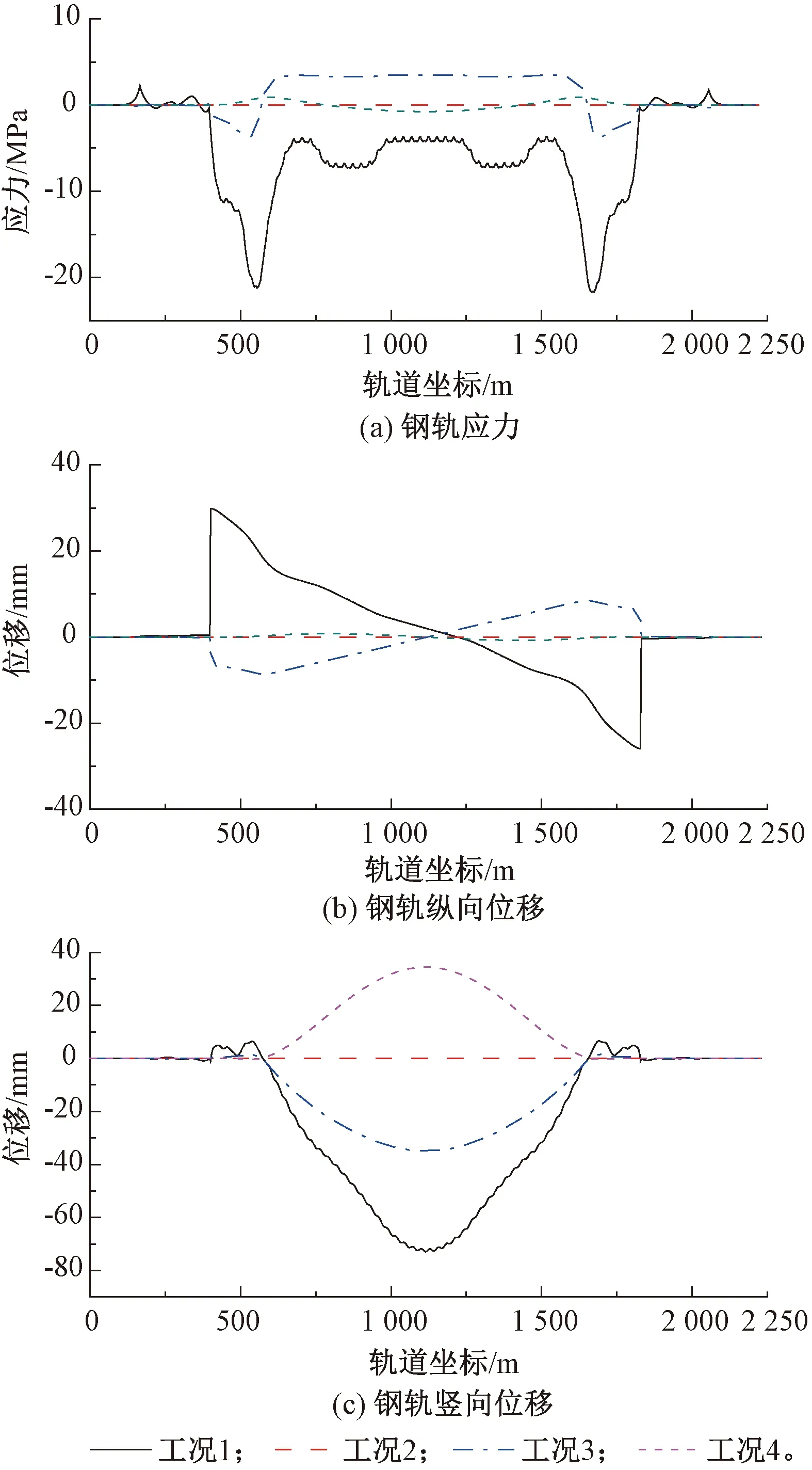
图6 部件温度变化对系统受力和变形的影响
通过比较,悬索桥主梁温度变化时钢轨应力峰值达22.3 MPa,而主塔温度变化时钢轨应力几乎为0 MPa,主缆温度变化时钢轨应力峰值达3.5 MPa,吊杆温度变化时钢轨应力峰值达0.7 MPa。
悬索桥主梁温度变化时钢轨纵向位移峰值达29.6 mm,主塔温度变化时钢轨纵向位移基本为0 mm,主缆温度变化时钢轨纵向位移峰值达8.5 mm,吊杆温度变化时钢轨纵向位移峰值达0.8 mm。
主梁温降时钢轨竖向位移峰值为向下74.5 mm,主塔温降时钢轨竖向位移基本为0 mm,主缆温降时钢轨竖向位移峰值为向下34.9 mm,吊杆温降时钢轨竖向位移峰值为向上34.4 mm。
对墩顶水平力而言,悬索桥主梁和主缆温度变化时制动墩墩顶水平力为498.2、116.3 kN,主塔和吊杆温度变化时制动墩墩顶水平力极小。
5.2 列车制动
假设列车制动作用下,设在两悬索桥主塔处的粘滞阻尼器可以完全约束梁体纵向位移[17]。考虑两线同时制动,制动力率取为0.25[11],计算钢轨应力及梁轨相对位移包络图,见图7。由图7可见,在制动力作用范围两端钢轨应力达到最大值,最大拉应力为10.0 MPa,最大压应力为12.4 MPa。梁轨纵向相对位移响较小,梁轨相对位移最大值出现在悬索桥主塔处,为1.3 mm。工况一情况下北制动墩墩顶水平力最大达605.2 kN。
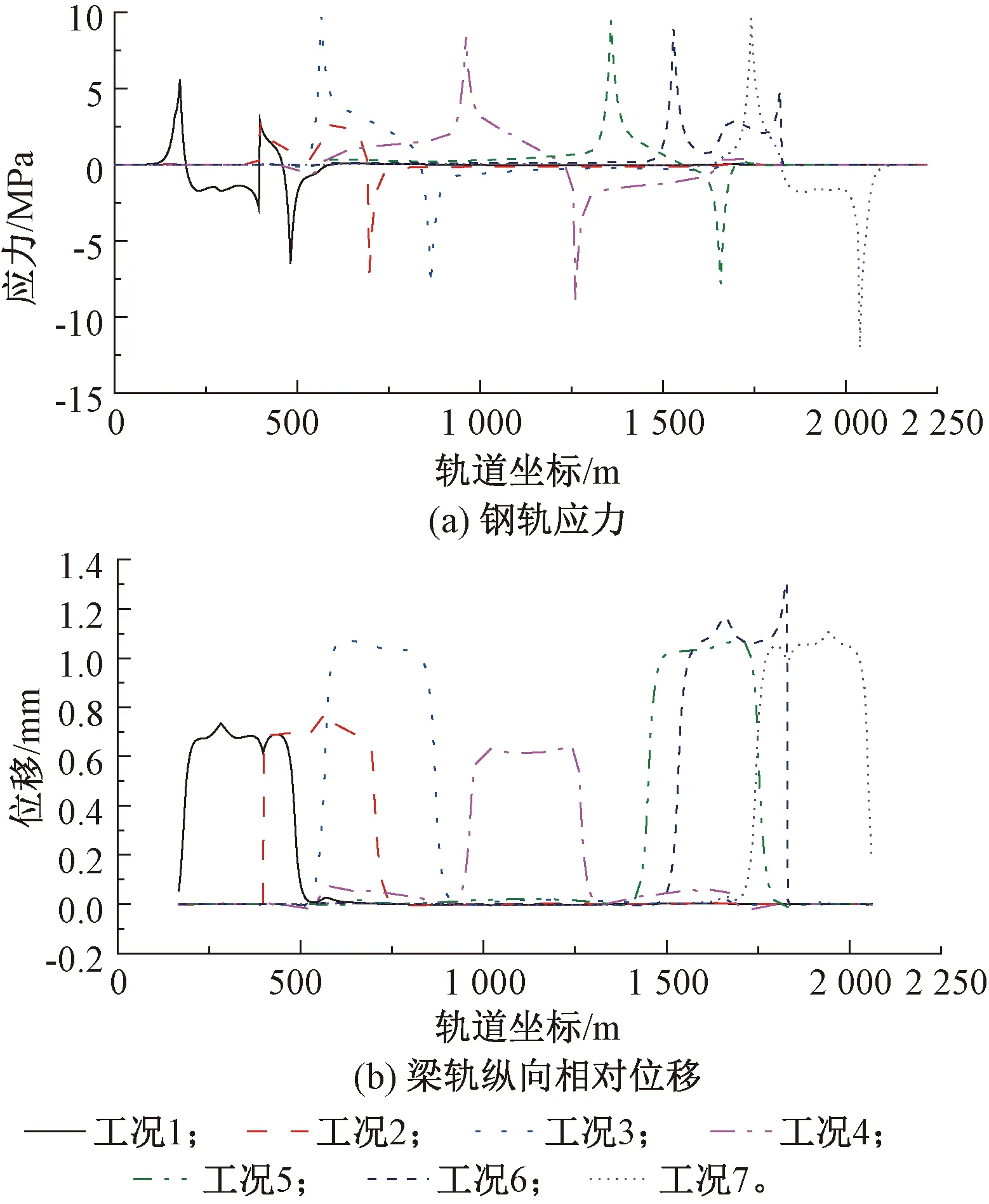
图7 制动力计算结果
5.3 挠曲力
考虑四线同时加载,两线客运专线采用0.8UIC,两线城际铁路采用0.6UIC,计算钢轨应力、钢轨纵向位移、梁轨相对位移和钢轨竖向位移包络图,见图8。
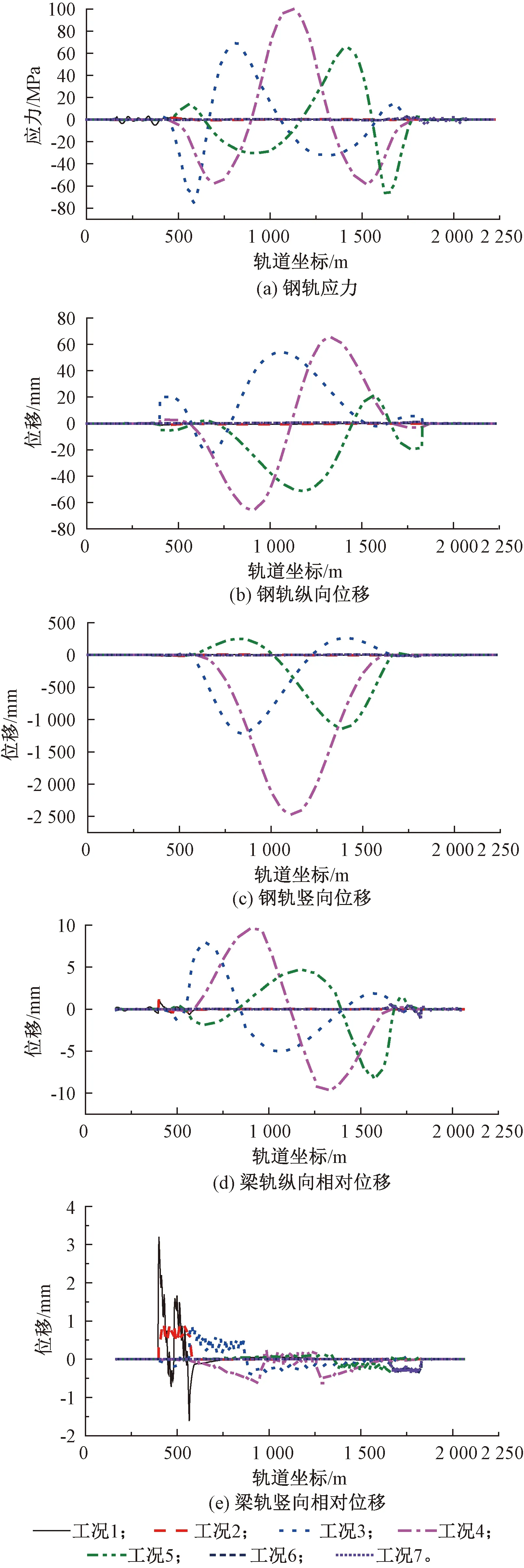
图8 挠曲力计算结果
由图8可见,在竖向荷载作用下,悬索桥跨中跨中附近钢轨竖向变形达2 468.6 mm,桥梁与轨道之间存在着较大的纵向相对位移。挠曲力下梁轨纵向相对位移出现在加载范围两端,达9.7 mm,梁轨竖向相对位移较小,在悬索桥主梁两端为3.4 mm。
由于桥梁与轨道之间的纵向相对位移较大,钢轨承受着极大的应力。钢轨最大拉应力出现在悬索桥跨中处为98.6 MPa,最大压应力出现在北侧主塔为74.5 MPa。钢轨最大纵向位移出现在挠曲力加载范围两端附近为63.5 mm。
5.4 风荷载
在悬索桥主塔施加纵向风荷载,用来研究风压对大跨度悬索桥上无缝线路的影响。根据TB 10002.1—2005《铁路桥涵设计基本规范》[18]中风荷载的取值公式为
W=K1K2K3W0
(2)
式中:W为风荷载强度;K1为外形特征系数;K2为高度特征系数;K3为地貌特征系数;W0为基本风压。
采用文献[18]取值,其风荷载强度为1.5 kN/m2,计算钢轨应力及钢轨纵向位移,见图9。

图9 风荷载计算结果
该悬索桥所在区域的风压作用下,钢轨附加应力极小,在悬索桥主梁两端最大为0.001 MPa,钢轨纵向位移极小。
6 结论
本文以某(84+84+1 092+84+84)m大跨度铁路悬索桥为工程背景,首次建立了考虑主缆、吊杆、钢桁梁、正交异形板、以及相邻桥跨结构的大跨度悬索桥与四线轨道相互作用模型,研究了温度、竖向荷载和列车制动作用下铁路悬索桥无缝线路纵向力的分布特征及规律。主要结论包括:
(1)在悬索桥梁端设置钢轨伸缩调节器后,可大幅降低悬索桥梁端钢轨应力和制动墩墩顶水平力。悬索桥主缆温降对钢轨应力有一定影响,考虑桥梁温降,桥跨范围内钢轨应力峰值为22.3 MPa,吊杆和桥塔温降对系统受力影响极小。
(2)当制动力完全作用在悬索桥主跨时,钢轨最大拉应力为10.0 MPa、最大压应力为12.4 MPa。梁轨纵向相对位移最大为1.3 mm。
(3)由于铁路悬索桥竖向刚度较小竖向荷载作用下,跨中钢轨竖向位移达2.4 m,挠曲力代替伸缩力成为控制荷载,其钢轨应力峰值达98.6 MPa,列车在桥上运行产生梁轨快速纵向相对位移达9.7 mm,有砟轨道存在失稳风险。
