高速列车车轮多边形磨耗安全限值研究

2021-05-13张富兵邬平波吴兴文汪群生李凡松

铁道学报 2021年3期

张富兵，邬平波，吴兴文，汪群生，李凡松

(1.西南交通大学牵引动力国家重点实验室，四川成都 610031；2.重庆文理学院智能制造工程学院,重庆 402160)

近些年国内高铁技术突飞猛进，从最早的引进消化吸收阶段，已经进入到现在完全掌握并可以再创新的阶段，高铁已经成为我国高端装备制造业的名片。我国现在是全球高铁运营里程最多的国家，最新投入运营的“复兴号”运行速度为350 km/h，因此国内的高铁具有运行距离长、行驶速度快等特点。在国内这些年运营过程中，一些亟待解决的问题也逐渐浮现出来，其中一个重要的问题就是车轮多边形现象[1]。车轮多边形是指轨道车辆车轮名义滚动圆周向不均匀磨耗的现象[2-3]。车轮多边形现象会增大轮轨作用力，加剧车辆系统的振动，从而会导致转向架系统关键部件的寿命大大缩短。车轮多边形不仅仅存在于我国高速铁路，它是一个世界性的难题。

早在1974年，Jenkins等[4]就研究了不同类型不圆化车轮的冲击载荷，由此提出了车轮设计的的改进方案。1992年在加拿大温哥华列车上测量到车轮多边形现象，Kalousek等[5]通过试验测量和仿真计算，提出了可以通过修正钢轨和车轮的型面来改善车轮多边形现象。Brommundt[6]通过数值计算和动力学模型研究了多边形现象，认为车轮的初始误差和车轮转动惯量的相互作用导致了车轮多边形的产生。Morys等[7-8]研究车轮多边形产生的原因和演化规律，建立了ICE-1型高速列车的动力学模型，得出结论是车轮多边形会导致轮轨垂向力的大幅度变化，并且会激发轮对的弯曲模态，引发共振，最终加剧车轮多边形的发展。Mombrei等[9]从车轮的打滑负荷和车轮材料属性两方面研究了车轮不圆形成的原因，认为是载荷不均匀和材料分布不均匀导致了多边形的出现。Meywerk等[10]通过仿真计算的方式研究了车轮多边形的形成和发展演化规律，认为轮对的第一阶和第二阶垂向弯曲模态在车轮非圆化发展过程中也起着重要的作用。文献[11-12]通过各自建立的模型研究了车轮多边形现象，提出了不同的多边形形成机理。

罗仁等[13]建立了车辆-轨道系统动力学模型和车轮圆周磨耗预测相结合的耦合模型，用于研究高速车辆车轮多边形磨耗发展规律以及对车辆动力学性能的影响。陈光雄等[14]根据Yuan提出的建模方法，应用有限元软件ABAQUS建立了摩擦系统的动力学模型，研究了轮轨系统的黏-滑振动特性、摩擦系数、轨枕垂向支撑刚度对车轮多边形磨耗的影响。李伟等[15]以地铁车辆为研究对象分析了车轮多边形的产生机理，通过试验和仿真相结合的方式说明了一阶弯曲模态是形成车轮多边形现象的主要因素。吴磊等[16]研究了车轮多边形对车辆运行安全性能的影响。王忆佳[17]研究了车轮多边形对车辆系统动力学性能的影响，并根据轮轨垂向力提出了相应的安全限值。刘国云[18]、陈伟等[19]也应用动力学仿真研究了车轮多边形的安全限值问题，提出的安全限值也是基于轮轨垂向力。文献[20-21]建立了柔性轮对的车辆-轨道动力学模型，研究了车轮多边形对轮轨力和车轴损伤的影响，指出车轮多边形会激发轮对的弯曲模态，从而产生恶劣影响。西南交通大学动力学与强度团队的戴焕云等[22-23]，应用金属切削中切痕形成理论分析研究高速铁路车轮多边形磨损，提出基于切削原理的高速列车车轮多边形磨耗机理及转向架车轮间钢轨第三阶模态振动是导致高速列车车轮高阶多边形磨耗的主要原因，并在国际会议上正式提出。

综上可知，对于车轮多边形的研究主要集中在2个方面：①车轮多边形形成机理;②车轮多边形对车辆系统的影响。车轮多边形的形成机理尚未完全掌握，国内外学者的意见也并不统一，主流理论可以分为3种：车轮多边形的形成与轮对模态相关；与初始缺陷相关；与轨道振动相关。在形成机理没有完全掌握之前，车轮多边形的出现不能完全避免。

部分学者对车轮多边形产生的影响进行研究，发现车轮多边形对车辆的安全运营具有很不利的影响，因此针对车轮多边形的安全限值进行了研究，如文献[17-19]用动力学模型提出了不同阶次多边形的安全限值。可以发现上述研究有个共同点，即都是根据轮轨垂向力这一制约因素提出的安全限值。本文通过建立车辆-轨道刚柔耦合动力学模型和试验台试验相结合的方式研究了车轮多边形对车轴动应力的影响规律，并且根据车轴许用应力和轮轨垂向力提出了不同阶次多边形的安全限值。

1 车辆-轨道刚柔耦合动力学模型

车轮多边形对轮轨之间的作用力有很大的影响，因此，只考虑轮对的柔性还不够，轨道动态响应的影响也是必须要考虑的。车辆系统和轨道能够耦合到一起的关键，是柔性轮对模型和轨道模型建立交互，图1阐述了含有柔性轮对的车辆系统动力学模型和轨道模型耦合的方案思路。将动力学模型中计算获得的动态轮轨力作为轨道的载荷输入，用于评估轨道的响应。随后使用SIMAT(Simpack-Matlab)协同仿真接口将轨道位移响应集成到车辆模型中。

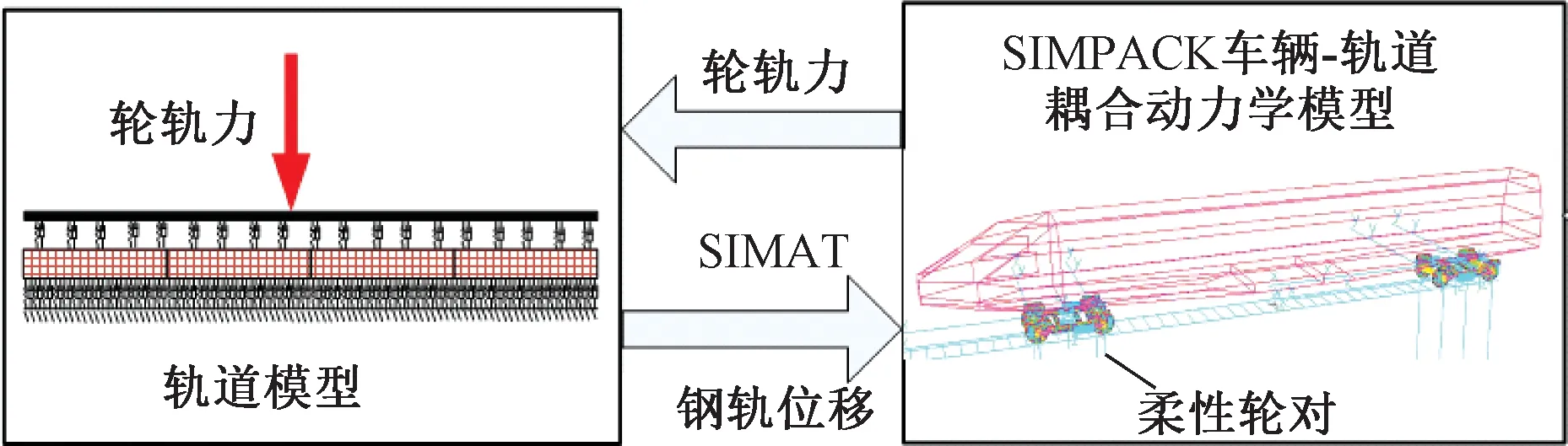
图1 车辆-轨道耦合模型

我国高速铁路大多采用无砟轨道形式，典型无砟轨道结构见图2，主要包括左右2条60 kg/m 钢轨、缓和轮轨冲击的扣件系统、高稳定性的轨道板、具有调整功能的CA砂浆层和路基等。在仿真模型中扣件和砂浆层通过弹簧-阻尼单元进行模拟，钢轨考虑为Timoshenko梁来模拟钢轨的振动行为，轨道板的弹性振动用实体单元方法模拟。下面对车辆模型和轨道模型进行了简单的介绍。

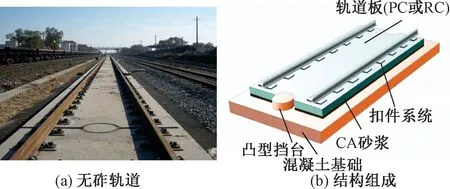
图2 无砟轨道及其结构组成

1.1 车辆模型

以某高速列车拖车为例，应用商业软件Simpack建立了拖车的动力学模型。整个车辆模型系统见图3，包含2个构架、1个车体、4条轮对和8个轴箱，以及相应的一系悬挂和二系悬挂。一系悬挂由轴箱进行定位，安装钢弹簧和垂向减振器；二系悬挂包括摇枕、空气弹簧、抗侧滚扭杆、二系垂向减振器、二系横向减振器、抗蛇形减振器以及横向止挡等。其中构架、轴箱、轮对都考虑为柔性体。

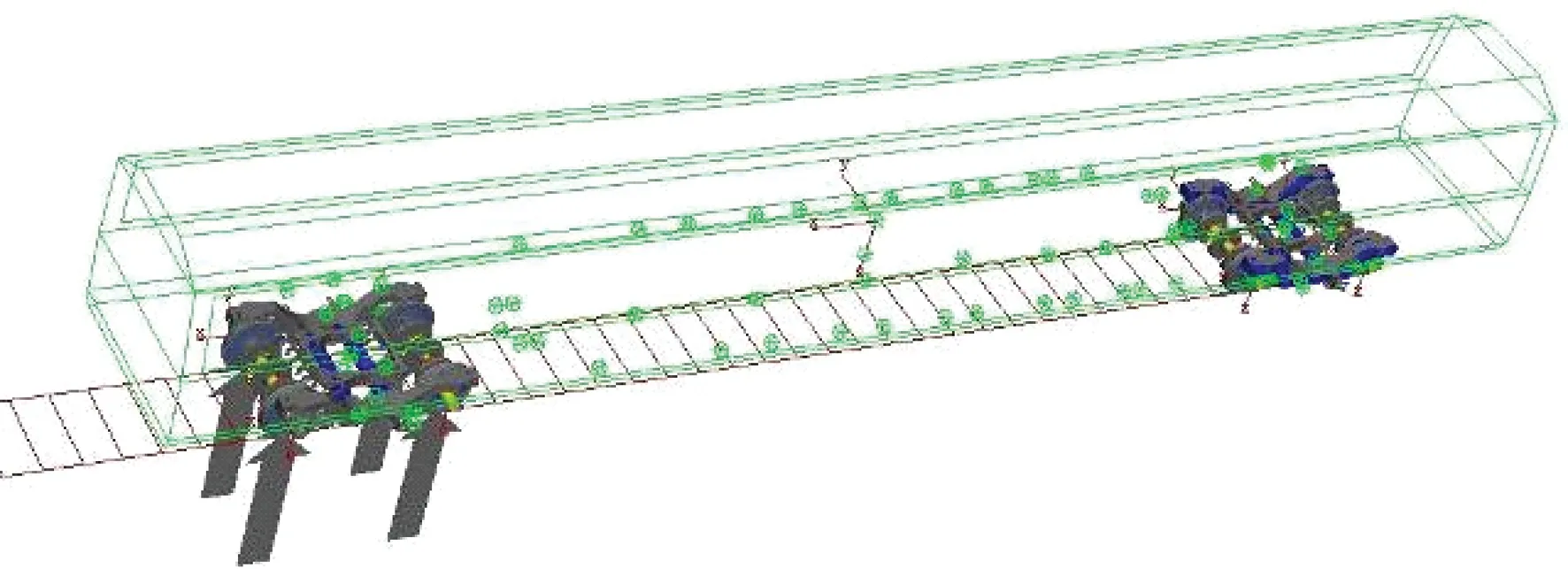
图3 车辆-轨道刚柔耦合动力学模型

1.2 钢轨模型

钢轨是由有限长度的Timoshenko梁表示，由扣件离散固定在轨道板上。该模型中设定钢轨长100 m，可以认为代替了无限长的钢轨，在工程上具有足够的精度和计算效率[24-25]。钢轨的两端是固定的，根据文献[20]中钢轨垂向、横向以及扭转振动微分方程的求解过程，即可以获得钢轨的响应。

1.3 轨道板模型

车轮缺陷或钢轨的不平顺引发的冲击力，通过钢轨、扣件传到轨道板，引发响应变形。轨道板的变形反过来又影响钢轨的位移，从而影响到轮轨接触力，而且这个影响是不可忽略的。考虑与扣件联接的垂向力以及砂浆层提供的垂向力建立了轨道板的有限元模型。

在本文研究中，轨道部分设定长100 m，每个轨道板长6.5 m，宽2.5 m，厚0.3 m。有限元模型中使用Solid 185单元进行离散，每个轨道板离散为45 000个单元。在Ansys平台进行计算，设置为自由边界条件。为了分析轨道板的变形响应，考虑了轨道板的前30阶振动模态，其固有频率最高达594.74 Hz。轨道板的部分模态见图4。

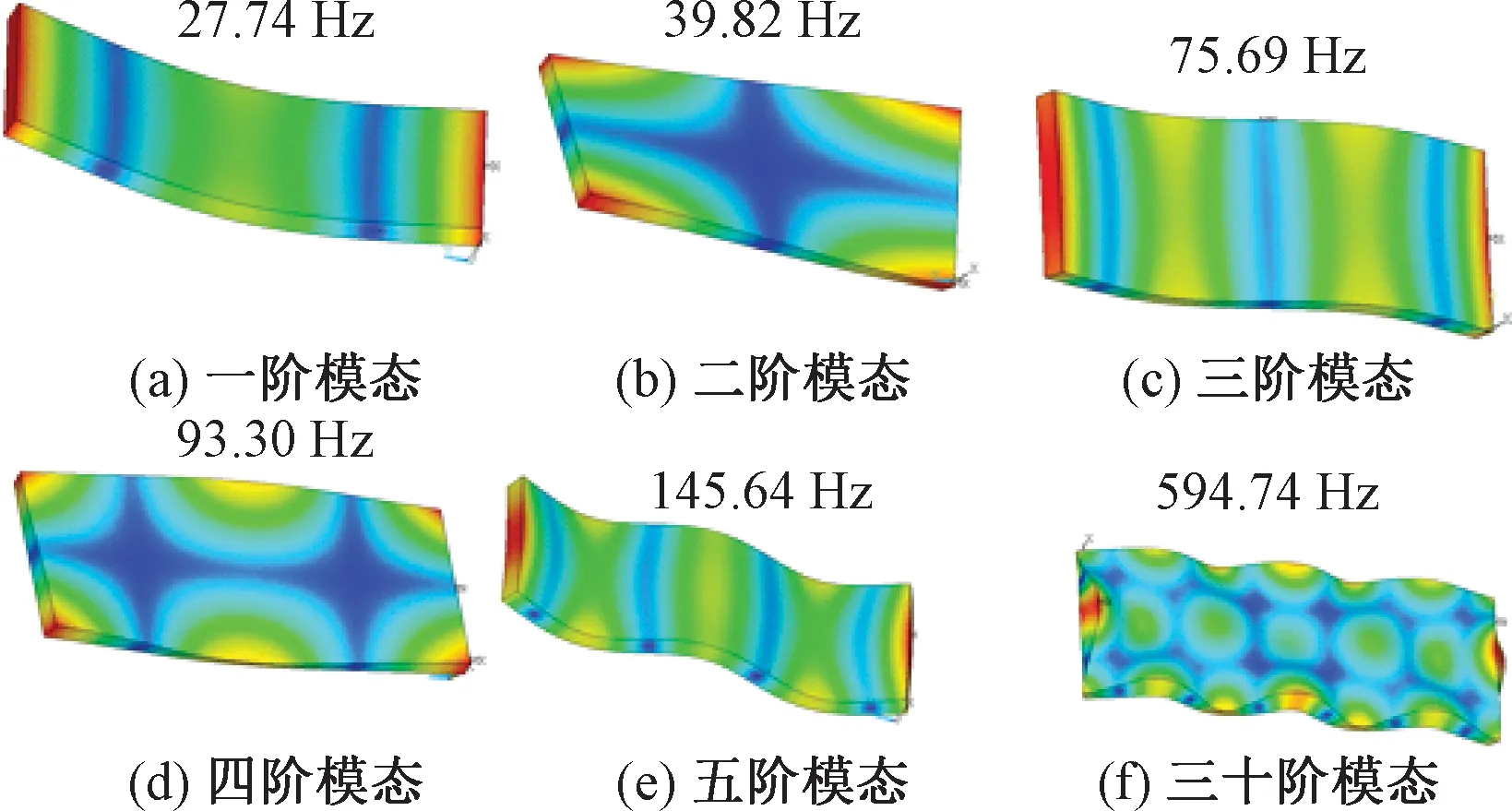
图4 轨道板的模态

2 动应力测试试验

2.1 试验台简介

本次试验依托西南交通大学牵引动力国家重点实验室的高频激振试验台,试验台工作原理见图5。试验台为高速旋转试验台，通过200 kW的电机进行驱动，模拟轨道的滚轮直径为600 mm，最高转速4 200 r/min，转向架上方有液压缸施加配重，液压缸单个量程为50 000 kg，2个液压缸最大可施加100 000 kg的载荷。电机与滚轮之间采用齿轮变速箱传动。轨道轮人工加工成多边形，就可以模拟线路上的车轮多边形或者轨道波磨。试验是单条轮对转动，另一条轮对固定于平台。本次试验轨道轮加工为波深0.05 mm的13阶多边形，试验转向架车轮轮径为920 mm，所以等效到车轮上为20阶多边形。

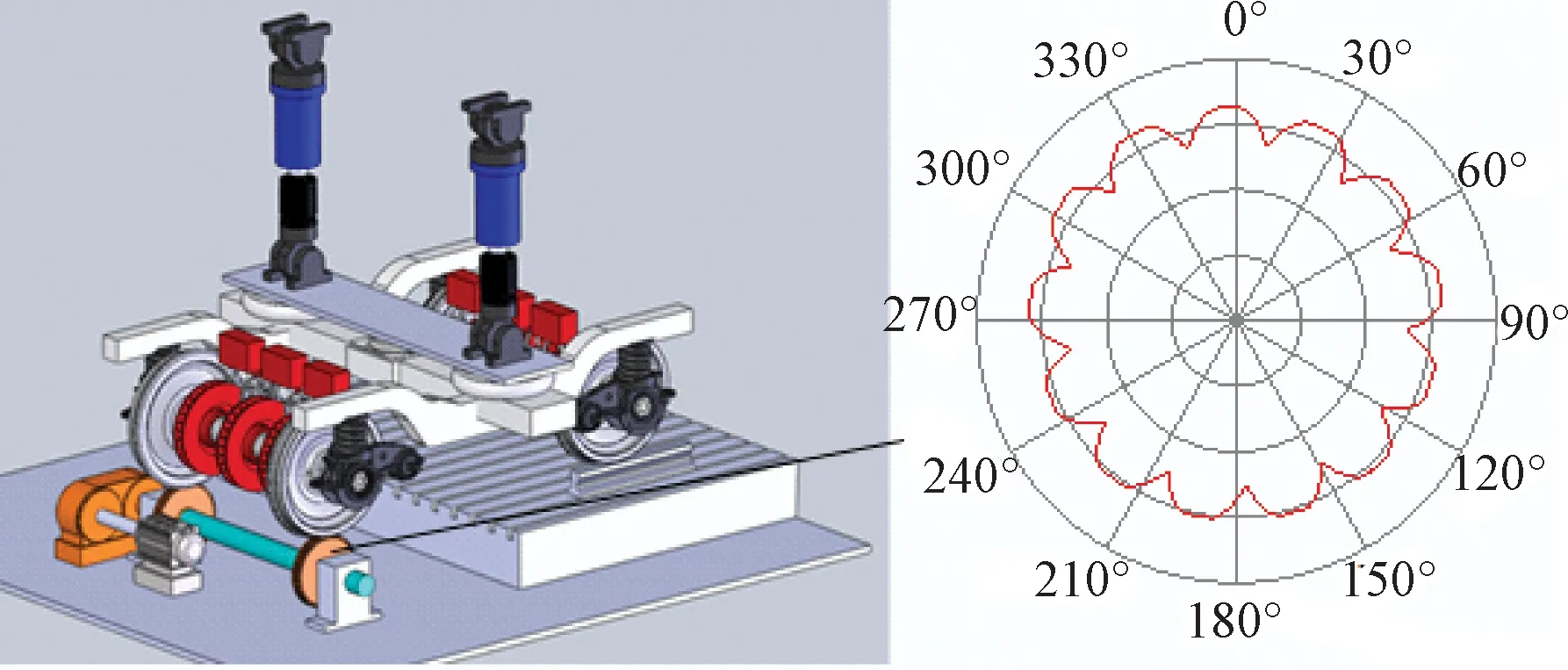
图5 试验台原理

2.2 试验设备简介

为研究车轮多边形对车轴应力的影响，在高频激振试验台搭载拖车转向架进行了车轴动应力数据采集试验。高铁车轴在运行过程中是高速旋转的，常规的有线数据采集系统无法完成试验。因此，实验室引进了瑞士Interfleet公司的无线遥测数据采集系统。无线数据采集系统由加速度传感器(或应变片)、应变调理模块、热电偶、编码器、ICP调理模块、热电偶信号调解模块、供电电源及端子、信号传输器等组成。其工作原理是将加速度传感器或者应变片粘贴到被测试设备上，传感器通过对应的调理模块与编码器连接，编码器通过信号传输器将采集的信号无线传输给用户。车轴上设备通过电磁感应方式进行供电。

2.3 试验数据分析

试验运行速度为0～320 km/h，图6为轮座过渡圆弧处应力时域图，速度曲线见图7。应力时频图见图8。从整体的时频图8(a)可以看出，应力数据主要由低频和高频两部分组成，低频是车轴的转频，高频部分是车轮多边形频率。低频部分颜色比高频部分重，所以低频部分的能量占主要成分。

图6 车轴应力时域图

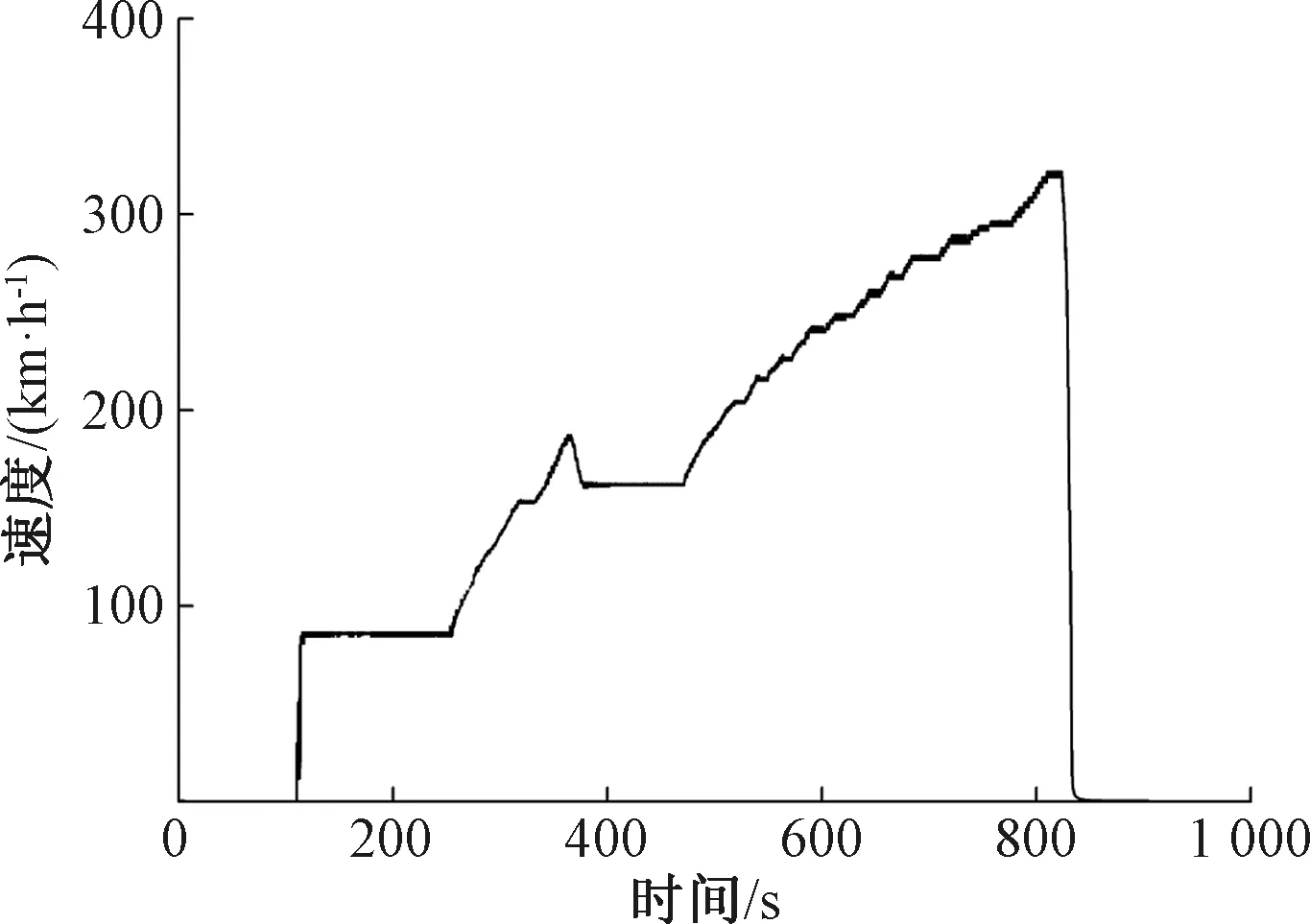
图7 速度曲线图

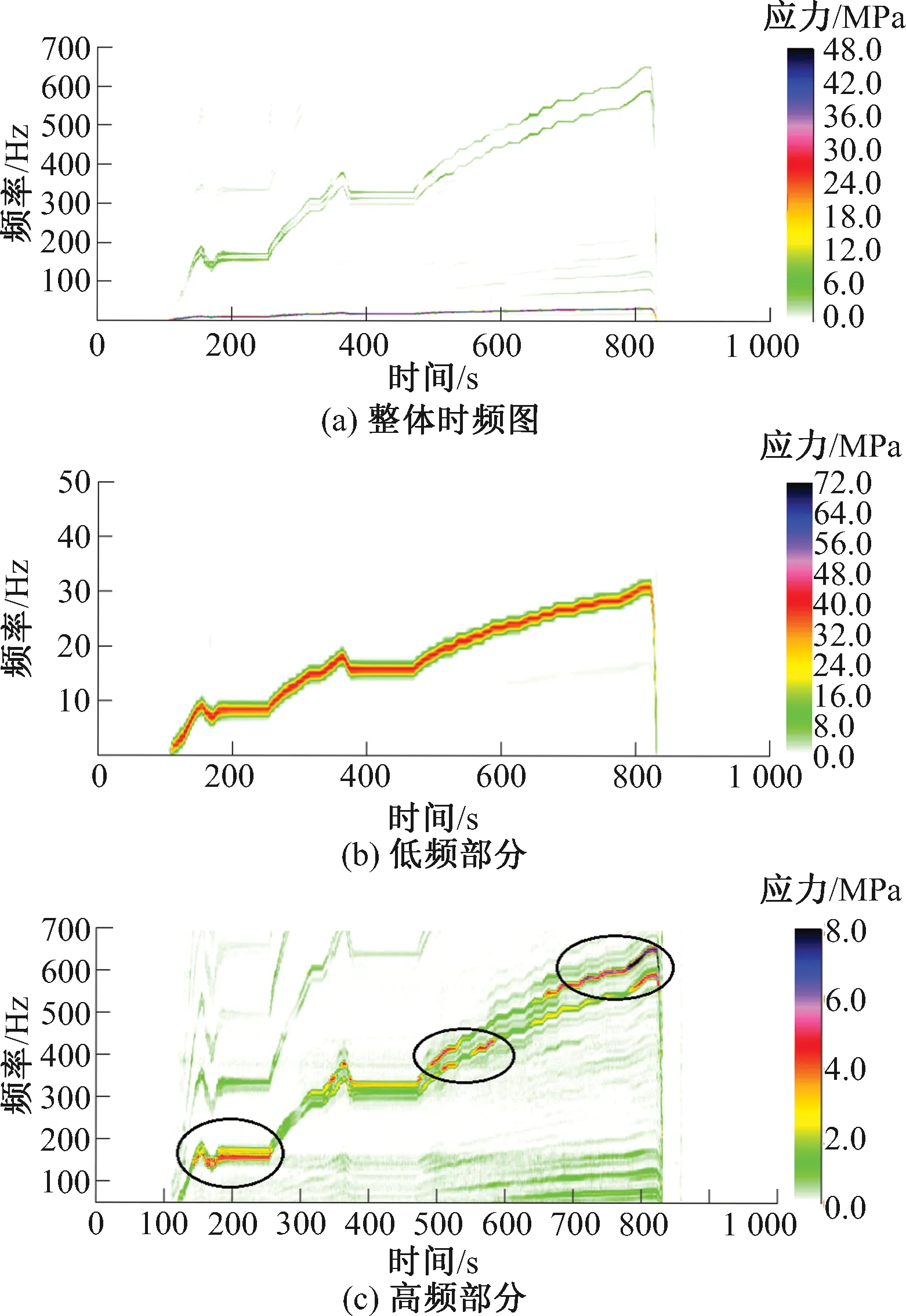
图8 应力时频图

为更好地分析频率特性，将时频图分成高频段和低频段分别来看，见图8(b)、图 8(c)，低频段只显示0～50 Hz部分，该频率的主要成分是车轴转频，可以看出该频率比较单一，并且和速度曲线图 7紧密相关。图8(c)高频段没有显示50 Hz以下的频率，由该图可以发现，在200 s左右、500～600 s、700～800 s 3个时间段内频率分别在170 Hz附近、400 Hz附近、600 Hz以上，表明这3个时间段内的能量明显比其他时间段大，出现了共振带。170 Hz是试验台固有模态共振导致的，这不是本文关注的重点，这里不予讨论。400 Hz附近的共振带是轮对二阶弯曲模态393 Hz所导致的，600 Hz以上的共振带是轮对三阶弯曲模态624 Hz共振导致的，轮对主要模态见图9。其中，二阶和三阶弯曲振型见图9(b)和9(d)。

图9 轮对主要模态

3 模型验证

在 Simpack 中，柔性体部件不仅可以动态的显示变形，还可以显示应力，即柔性体部件的动应力。但在显示动应力之前要做应力恢复，在有限元中利用模态频率响应分析计算静态应力，然后利用应力结果文件生成 Simpack 的应力恢复文件。

用动力学模型计算车轮多边形工况下车轴的动应力，与试验获得的动应力对比，验证动力学模型的准确性。动力学模型每次只能计算一个恒定速度的工况，所以试验数据截取同速度工况进行对比。

试验截取一段速度为250 km/h的车轴应力数据，选取的位置为轮座过渡圆弧处，此处的应力最大。试验数据见图10。仿真工况也为20阶多边形波深幅值为0.05 mm，计算速度为250 km/h，提取轮座处应力数据，见图11。

图10 速度为250 km/h试验数据

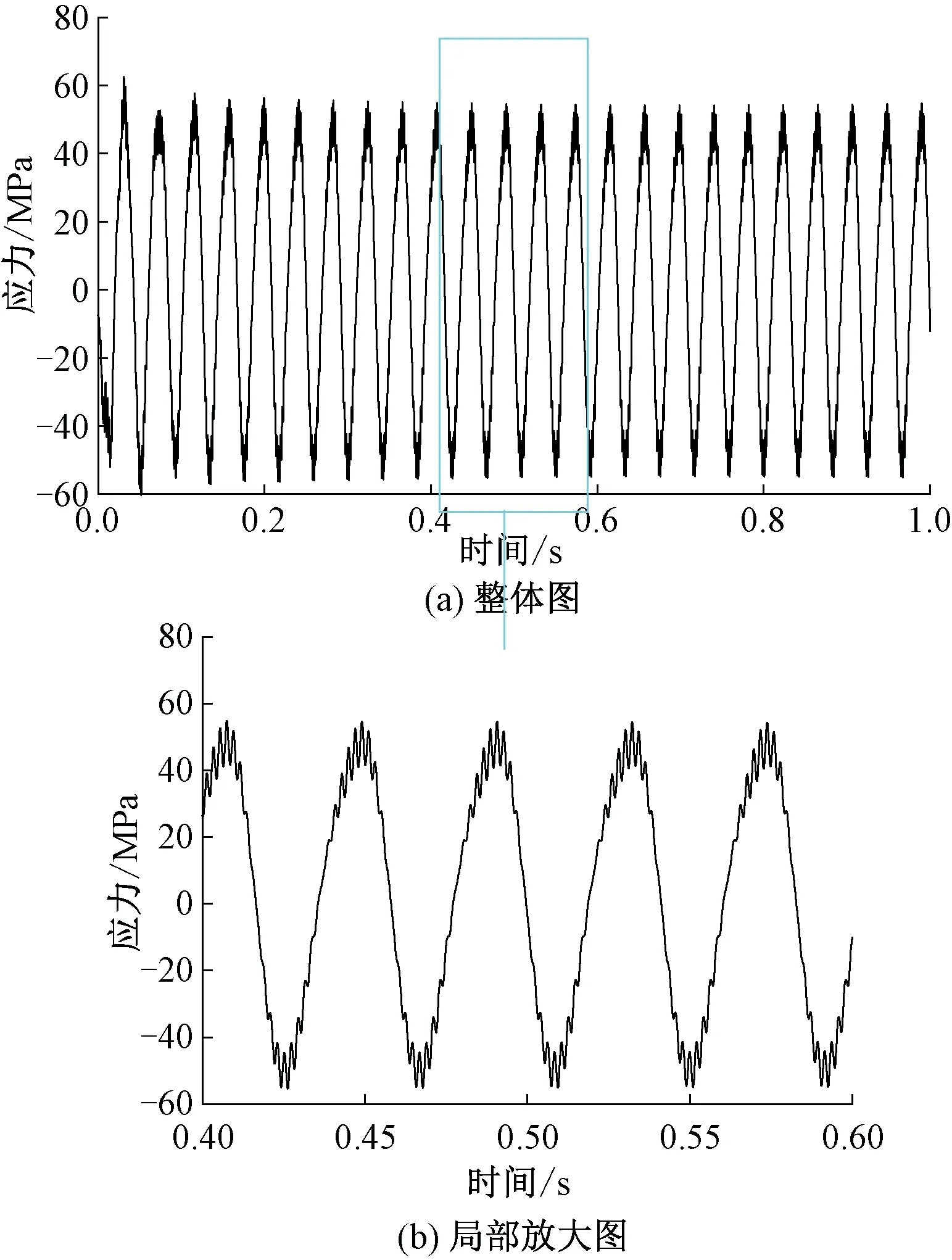
图11 速度为250 km/h仿真数据

从整体时域图及其局部放大的波形图来看，幅值的大小及波形都极为接近，定量分析来看，试验应力的均方根值为35.04 MPa，仿真应力的均方根值为34.62 MPa。对比试验应力和仿真应力的频域数据，见图12，两者最大主频都是车轴的转频23.9 Hz左右，试验应力的转频幅值为48.78 MPa，仿真应力的转频幅值为48.07 MPa，试验转频幅值略大。转频的倍频即47.8 Hz附近也有明显的幅值，此处试验数据幅值为2.99 MPa，仿真数据为6.01 MPa，仿真数据略大。综合而言低频段幅值相差不大。通过高频段的局部放大图可以发现，在457、505 Hz多边形激励频率附近有明显幅值，并且幅值极其接近，都在2、3 MPa左右，仿真数据稍大。

通过仿真和试验数据对比，说明该动力学模型计算结果都具有比较高的准确性和可信性。

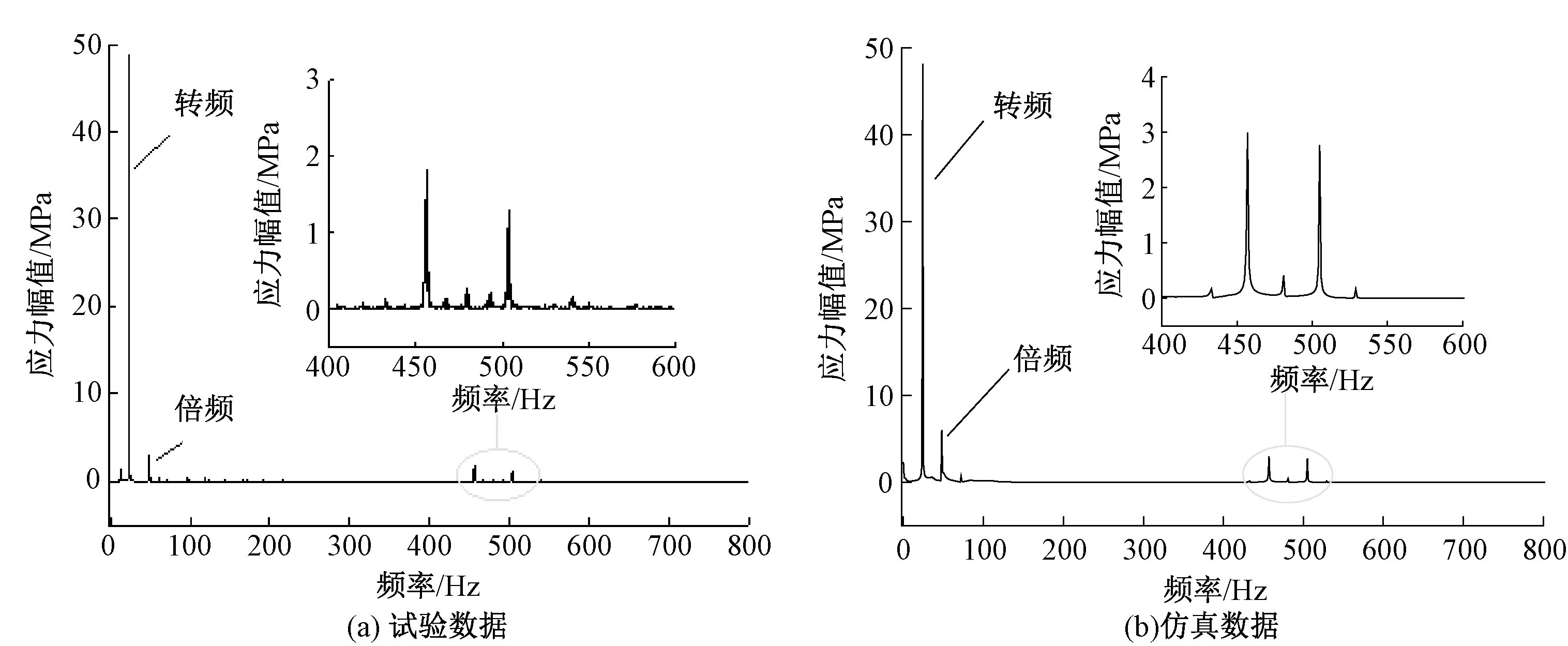
图12 数据频域图

4 基于车轴许用应力的多边形限值研究

通过以上试验数据分析可以确定，车轮多边形导致的轮轨高频冲击会对车轴应力产生影响。多边形车轮和理想车轮的车轴应力对比见图13。

图13 多边形车轮和理想车轮对比

通过对比可以说明，在没有多边形的情况下，车轴的弯曲应力主要是由车体和构架重力作用引起的静载荷导致的，其频率是由转频决定的。车轮多边形下应力多了一个高频成分。静载荷部分是基础，其幅值一般是不会改变的，高频部分的幅值决定了最终应力的大小。高频部分应力的大小和很多因素有关，本节研究了不同速度、不同波深、不同多边形阶次下车轴应力的变化情况,见图14。

图14 车轴最大应力随速度的变化关系

图14分别列出了12、15、18、20、22、25阶车轮多边形下车轴最大应力随速度的变化趋势，其中波深选取了0.02、0.05、0.07、0.1、0.15、0.2、0.3 mm进行计算。通过对比同一张图中，不同波深的应力变化情况可以看出，车轴应力的幅值受多边形波深的影响很大，波深越大应力越大。通过分析不同阶次运行过程中应力的变化规律可以发现，在低速和高速的时候应力都有一个突然增大的波峰，应力幅值要比起其他速度明显大很多，具体结果见表1。

表1 不同阶次下2个应力波峰对应的速度

可以看出，随着阶次的增大2个波峰都是往低速方向移动的，为了更明显的看出这个趋势，将0.3 mm波深各个阶次的应力变化情况绘制到同一个坐标系中，见图15。

计算各阶车轮多边形的激励频率计算式为

(1)

式中：f为频率；v为运行速度；n为多边形的阶次；d为车轮轮径，取0.92 m。

分别计算不同阶次下2个波峰在对应速度下的激励频率，可以获得12阶多边形对应的2个频率为81、415 Hz；15阶多边形对应频率为86、404 Hz；18阶多边形对应频率为86、407 Hz；20阶多边形对应频率为77、404 Hz；22阶多边形对应频率为85、402 Hz；25阶多边形对应频率为72、409 Hz。可以发现虽然阶次和速度不同，但是各阶多边形2个波峰对应的激励频率比较集中，第1个波峰频率集中在72～86 Hz之间，第2个波峰的频率集中在402～415 Hz之间。

根据轮对的模态计算结果，一阶弯曲模态频率为82 Hz，二阶弯曲模态频率为393 Hz，另外432 Hz存在扭转模态，见图9(a)～9(c)。

对各阶多边形(0.3 mm波深工况)第1、2个波峰的应力时域数据进行傅里叶变换，结果见图16。由图16(a)可见，应力组成的主要频率成分，除了转频，高频部分就集中在390、430 Hz这2个频带附近。因此可以确定第2个波峰是由于各阶多边形在402～415 Hz的激励频率激发了393 Hz的二阶弯曲模态和432 Hz的扭转模态，导致车轴的应力急剧增大。并且可以看出400 Hz附近多边形共振的幅值已经超过了转频的幅值，说明0.3 mm波深共振的时候，高频部分占了主要成分。

由图16(b)可见，每个阶次的应力组成分为2部分，一部分是转频，另一个部分频率较高的集中在80 Hz频带附近，这是由于82 Hz的一阶弯曲模态被激发导致的。

图16 波峰频域图

波深对应力的影响很大，同时共振条件下应力水平又会急剧增大，所以当波深大到一定程度车轴的应力就会超过设计的许用应力。国内车轴设计参考标准BS EN 13103—2009[26]和BS EN 13104—2009[27]，其中对空心拖车车轴EA4T材料的许用应力有如下规定，见表2。表2中，区域1：轴身、滑动轴承座、过渡区域、圆角处、其他摩擦密封、凹槽底面；区域2：除了轴颈和滑动轴承座的所有座；区域3：轴颈(滚动轴承下)；区域4：空心轴内腔。

表2 拖车空心车轴的最大许用应力(EA4T钢)

标准规定EA4T拖车车轴轴身位置的最大许用应力为180 MPa，从图15(a)～15(f)可以发现，当波深达到0.3 mm的时候，车轴的最大应力就已经超过了许用应力。那么存在某一波深，其最大应力刚好达到180 MPa，这个波深便可作为根据车轴强度提出的多边形限值。经过大量计算得到了不同阶次下，根据车轴强度得出的车轮多边形安全限值见表3。

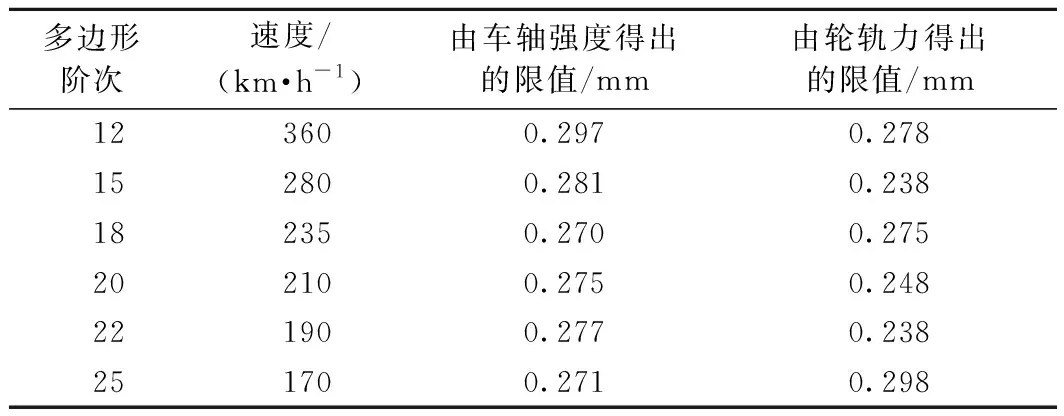
表3 安全限值对比

图17 车轮多边形的轮轨垂向力最大值随速度关系

5 基于垂向轮轨力的多边形限值研究

在高速运行过程中，车轮多边形会加剧轮轨垂向作用力，本节分析了不同波深、不同阶次多边形和速度等因素对轮轨垂向力的影响。

图17为18、25阶车轮多边形的轮轨垂向力最大值随速度的变化趋势，其中分别计算了不同波深下的变化趋势。可以看出轮轨垂向力和应力变化趋势有类似的地方，18阶多边形和25阶多边形分别在50 km/h和40 km/h出现第1个轮轨力波峰，在230 km/h和160 km/h出现第2个轮轨力波峰，出现波峰的位置和应力波峰相差不大。与应力变化趋势不同的是，轮轨垂向力在第2个波峰之后，急剧上升，此时的轮轨发生了分离，出现了跳轨现象，从而产生巨大的轮轨力冲击。

轮轨垂向力是车辆系统动力中衡量安全性的重要指标，很多学者[17-19]根据规范95J01—L《高速试验列车动力车强度及动力学性能规范》[28]规定的高速列车轮轨垂向力不应超过170 kN，提出了车轮多边形的安全限值。笔者也根据此指标计算了12、15、18、20、22、25阶在速度区间100～360 km/h的安全限值，见图18。提取几个关键速度级下的多边形限值，见表3。

图18 由轮轨力得出的多边形波深限值

对比由车轴强度和轮轨垂向力提出的安全限值可以发现， 12、15、20、22阶多边形，根据轮轨力提出的限值要比根据车轴应力提出的安全限值要小，这说明当轮轨力达到标准限值170 kN的时候，车轴应力小于许用应力180 MPa，这时根据轮轨力提出的限值是安全的；在18阶和25阶车轮多边形的时候，根据轮轨力提出的安全限值都要大于根据车轴强度提出的安全限值，也就是说当轮轨力达到安全限值170 kN之前轮轴的应力已经超过了车轴许用应力180 MPa。