梯度厚度多胞管的轴向冲击性能分析和优化设计

周俊先，陈秉智，秦睿贤

(1.大连交通大学 材料科学与工程学院,辽宁 大连 116021；2.大连交通大学 机车车辆工程学院,辽宁 大连 116021)

金属薄壁管件常被用作轨道车辆的吸能装置，如车钩中的压溃管和车辆端部的吸能梁[1-2]。传统吸能管(方形、圆形和多边形管)存在许多不足，如压溃形态不稳定且能量耗散效率较低，已无法满足先进交通工具对被动安全装置的要求。蜂窝铝[3]和泡沫铝[4-6]结构可以有效改善这种局限，因此被一些学者广泛研究。此外，另一种改善传统管件耐撞性局限的思路是在管件内部增加筋板使管件截面具有多胞构型[7-9]。相比于传统管件，多胞管在载荷稳定性和吸能效率方面均有了显著提升。但多胞结构的吸能潜力并未被充分挖掘，本文将梯度厚度引入到多胞管中并对其截面进行结构优化，进一步提升其吸能效率及耐撞性能。

陈伟刚等[7]最先运用超折叠单元理论分析了多胞管的压溃行为。他们提出了一种简化的折叠机制并在理论上分析了单胞、双胞和三胞矩形薄壁管件在轴向冲击下的力学特性。作为该研究的延伸，同样是基于简化的折叠机制，程耿东等[8]将方形等胞多胞管的截面划分为3个基本元素——L形、十字形和T形部件，并建立了相应的平均撞击力一般理论预测模型。同时，王忠刚等[9]基于复杂的运动学许可模型，对多胞管的撞击行为进行了理论分析，得到了更为精确的平均撞击力预测模型。此外，张雄等[10]推导了具有任意中心角的三板单元和四板单元的平均撞击力方程，基于这些方程可以预测具有任意截面构型的蜂窝和多胞结构的平均撞击力。

上述研究较全面地展现了多胞结构的力学性能。根据相关研究[8-9]，胞元数量是影响方形多胞结构耐撞性能的重要因素；当截面宽度和截面面积保持不变时，随着胞元数量的增加，多胞管吸能效率呈非线性增长，当胞元总数的增长超过某一定值，吸能效率的增长将逐渐放缓，直到几乎停止。因此，改善这种局限，使多胞管的吸能效率进一步提高具有广泛的研究意义。

最近，一些学者把目光投向了功能梯度薄壁结构。张辉等[11]设计了一种非均匀截面方管，并通过实验分析了其弯曲压溃行为。尹汉峰等[12]研究了方形功能梯度多胞管的吸能特性，并基于径向基神经网络法对其厚度梯度进行了优化。通过这些研究可以发现，梯度厚度设计可有效提升薄壁管件的力学性能。张雄等[13]通过改变方管截面的材料分布提出了2种梯度厚度方管：单面梯度(SSG)管和双面梯度(DSG)管。此外，他们还通过实验和数值模拟研究了这2种梯度厚度方管在轴向冲击下的变形模式和力学响应。与传统方管相比，DSG方形管可有效提升能量吸收效率(高达27.9%)。然而，目前还很少有研究尝试将截面梯度厚度与多胞管相结合。

梯度厚度设计对空心薄壁结构的性能提升已被充分验证[11,13]，因此有理由相信多胞管与梯度厚度设计的结合对改善结构的抗冲击性能具有积极作用。根据相关研究[13]，双面梯度厚度分布类型(DSG)比单面梯度厚度(SSG)更出色，具体表现为双面梯度方管拥有更稳定的压溃模式和更高的吸能效率，且由于DSG厚度分布类型是一种对称性材料分布类型，因此相比SSG类型不易发生畸形褶皱和结构撕裂[13]。本文尝试将双面梯度厚度(DSG)设计引入到多胞管中以改善结构的吸能效率。首先，对多胞管的能量吸收特性进行分析，确定合理的梯度分布规律。然后，基于4种胞元密度分别建立4组梯度厚度多胞管有限元模型，且每组模型中厚度梯度逐渐增大。基于显式非线性有限元分析软件Ansys/LS-DYNA对双面梯度多胞管进行了一系列数值仿真实验，以探索梯度厚度设计与多胞管的结合对结构耐撞性能的影响。最后，为了使这种新型管件的能量吸收效率最大化，将多胞管件截面离散为多个厚度参数并基于RBF神经网络法对截面的材料分布进行了初步的参数优化设计。

1 多胞管的吸能特性

Wierzbicki[14]最早运用超折叠单元理论分析了薄壁方管在轴向冲击下的耐撞性，并推导了方管的平均撞击力预测方程

Pm=13.06σ0B1/3t5/3

(1)

式中:Pm为平均撞击力理论值；σ0为材料的流动应力;t为壁厚;B为管件的截面宽度。

具有幂律硬化行为的材料流动应力可通过式(2)等效[4]

(2)

式中:σy为材料的屈服强度;σu为极限强度;n为材料的硬化指数。

图1 多胞方管的截面构型

为了将超折叠单元理论应用到双胞和三胞管上(见图1)，陈伟刚等[14]提出了一种简化的分析方式，这种方式并没有像Wierzbicki等的研究那样构建一个由梯形面、圆柱面、圆锥形面和移动塑性铰链组成的运动学许可模型，而是建立了一个由3个延展三角形单元和3个水平塑性铰链组成的简化折叠模型。延展单元的几何图形见图2(a)，图中展示了1个发生折叠的翼板，其宽度为c(单胞管宽度的一半)，厚度为t，长度为2H(一个折叠波长)。在折叠发生后，3个薄膜变形单元(1个延展2个压缩)在折角线附近产生，见图2(a)，同时还有3个旋转角分别为θ，2θ和θ的水平稳定塑性铰在该翼板上产生,见图2(b)。管件在一个折叠周期内的变形可产生多个基本折叠单元。因此，在一个折叠周期内，将管件的所有翼板所受外力等价于其内能，可以得到[7]

2HPmδ=Emembrane+Ebending

(3)

式中:δ为压溃距离系数;Emembrane、Ebending分别为在一个折叠周期内的薄膜变形能、弯曲能。对于参与折叠变形的1个翼板，其薄膜变形能可以通过对延展和压缩变形区域的面积进行积分获得

(4)

式中:M0为极限塑性弯矩,且有M0=σ0t2/4。

弯曲能等于所有稳定塑性铰链处耗散的能量之和[7]

(5)

式中:θi为每一个水平塑性铰的弯曲角度。为使问题简化，假设1个翼板在1个折叠波长2H内完全压溃，见图2(c)，3个稳定塑性铰的弯曲角度分别为π/2、π和π/2，将3个角度带入式(5)，可得[7]

Ebending=2πM0c

(6)

根据陈伟刚等的研究，将一个折叠周期内管件的弯曲能和薄膜变形能带入式(3)并求解，最终获得了单胞、双胞和3胞管的平均撞击力理论公式[7]

(7)

式中:N为翼板的总数量，对于单胞、双胞、三胞管N分别为8、14、20;A为管件截面面积。

图2 折叠单元的简化几何图形

后来，程耿东等[8]对这个简化模型做出了修正，并将其推广到了方形等胞多胞管上。为分析整个多胞管的能量吸收，他们将管件截面划分成3个基本构件：L形、T形、十字形构件，见图3。假设1个具有n×n个胞元的多胞管，其截面可以被划分成m1个L形构件、m2个T形构件和m3个十字形构件；m1、m2和m3可通过下式表示

m1=4m2=4(n-1)m3=(n-1)2

(8)

图3 多胞管的截面划分

多胞管在1个折叠周期内的弯曲能量依然可通过式(5)预测，于是有

Ebending=2πM0LC

(9)

式中:LC为所有翼板的总长，即管件的截面周长。此外，多胞管在1个折叠周期内的薄膜变形能则要根据3种基本构件各自的变形特征分别讨论。

根据陈伟刚和Wierzbicki等的研究，L形折角的2个翼板均参与了薄膜变形，因此对其延展和压缩区域的面积进行积分可得到其薄膜变形能为[7]

(10)

计算十字形构件的薄膜变形能要相对复杂，程耿东等根据对十字形构件的压溃行为研究发现，在1个折叠周期内，十字形构件的4个翼板中2个发生延展变形，另外2个发生压缩变形。发生延展变形和压缩变形的翼板见图4。对十字形构件的所有薄膜变形区域进行积分可得其薄膜变形能量为[8]

(11)

同时，在一个T形构件的3个翼板中，1个发生延展变形，1个发生压缩变形，还有1个未发生薄膜变形。因此，T形构件的薄膜变形能量为[8]

(12)

图4 薄膜变形能单元的简化几何图形

因此，多胞管在1个折叠周期内的薄膜变形总能量为

[16+32(n-1)+16(n-1)2]M0H2/t

(13)

将式(9)和式(13)代入式(3)可最终解得方形多胞管的平均撞击力理论表达式[8]

(14)

在管件压溃变形过程中，薄膜变形相比弯曲变形在能量耗散上更加高效，且根据上面的分析，对3种基本构件(L形、T形和十字形)来说，薄膜变形区域均发生在翼板交汇区域，即图3中的红色圆圈内区域。因此，将双面梯度厚度引入到多胞管中，使更多的材料集中在翼板交汇区有希望提升多胞管的吸能效率。这种双面梯度多胞的吸能特性将在下面通过数值仿真进行分析。

2 双面梯度多胞管的仿真分析

2.1 双面梯度多胞管的几何特征

根据第1节的分析，将双面梯度厚度引入多胞管后使3个基本构件的材料分布方式发生改变，构件截面见图5。这里采用了一种简单的材料分布方法：整个截面由2部分组成，分别为绿色的均匀厚度区域和灰色的梯度厚度区域。梯度厚度区的厚度为线性渐变，因此该区域有2个几何参数，分别为最大厚度t1和最小厚度t2。

图5 具有双面梯度厚度的3种基本构件的截面

2.2 有限元模型的建立

本节将运用非线性有限元分析软件Ansys/LS-DYNA对双面梯度多胞管的轴向冲击行为进行仿真分析。用于仿真分析的所有试件截面宽度B均为90 mm、长度L为160 mm，共考虑了4种胞元密度，分别为1×1、2×2、3×3、4×4。每种胞元密度下均采用了4种t1、t2的组合，以研究梯度厚度对4种多胞管的影响。其次，为直观地对比试件的吸能效率，所有试件质量保持一致，即试件截面面积均相等。试件采用了一种简明的命名方法，例如1×1(3.4,2.6)代表一个单胞双面梯度管，其t1、t2分别为3.4、2.6 mm。

所有试件采用相同的边界条件，见图6。碰撞过程被模拟为：管件底部固定在非移动刚性板上，并用另一个刚性板以10 m/s的恒定速度对其进行轴向撞击。速度的给定是通过在Initial模块中设置一个恒定的速度曲线来实现。非移动刚性板在横向、纵向和垂向的平动和转动自由度均被约束，移动的刚性板除了垂向(管件的轴向)平动自由度外其他自由度也被约束。碰撞模型中共考虑了2种接触行为，分别为面-面自动自接触(Automatic Single Surface)，模拟管件的自接触行为;管件与运动刚性板的面-面接触(Automatic Surface to Surface)，模拟管件与运动刚性板之间的接触行为。接触对的静摩擦和动摩擦系数均设为0.2。

图6 管件边界条件

试件的有限元模型采用六面体实体单元划分。根据经验和相关研究，沿管件长宽方向单元尺寸均为1 mm，并且在厚度方向划分三层网格可以保证足够的计算精度。压痕诱导槽的引入可以使得管件产生较合理的压溃模式同时降低初始峰值力。诱导槽深度为0.6 mm，位置距离管件上方1个折叠半波长H，见图6。

建模所采用的材料为挤压铝合金AA6060 T4[4]，其力学属性为：杨氏模量E=68.21 GPa、泊松比μ=0.3、初始屈服极限σy=80 MPa、强度极限σu=173 MPa。材料的应力-应变曲线见图7，该曲线可以通过n=0.23的幂律函数近似。在软件中采用弹塑性材料模型，并将材料本构以曲线的形式输入到模型中。

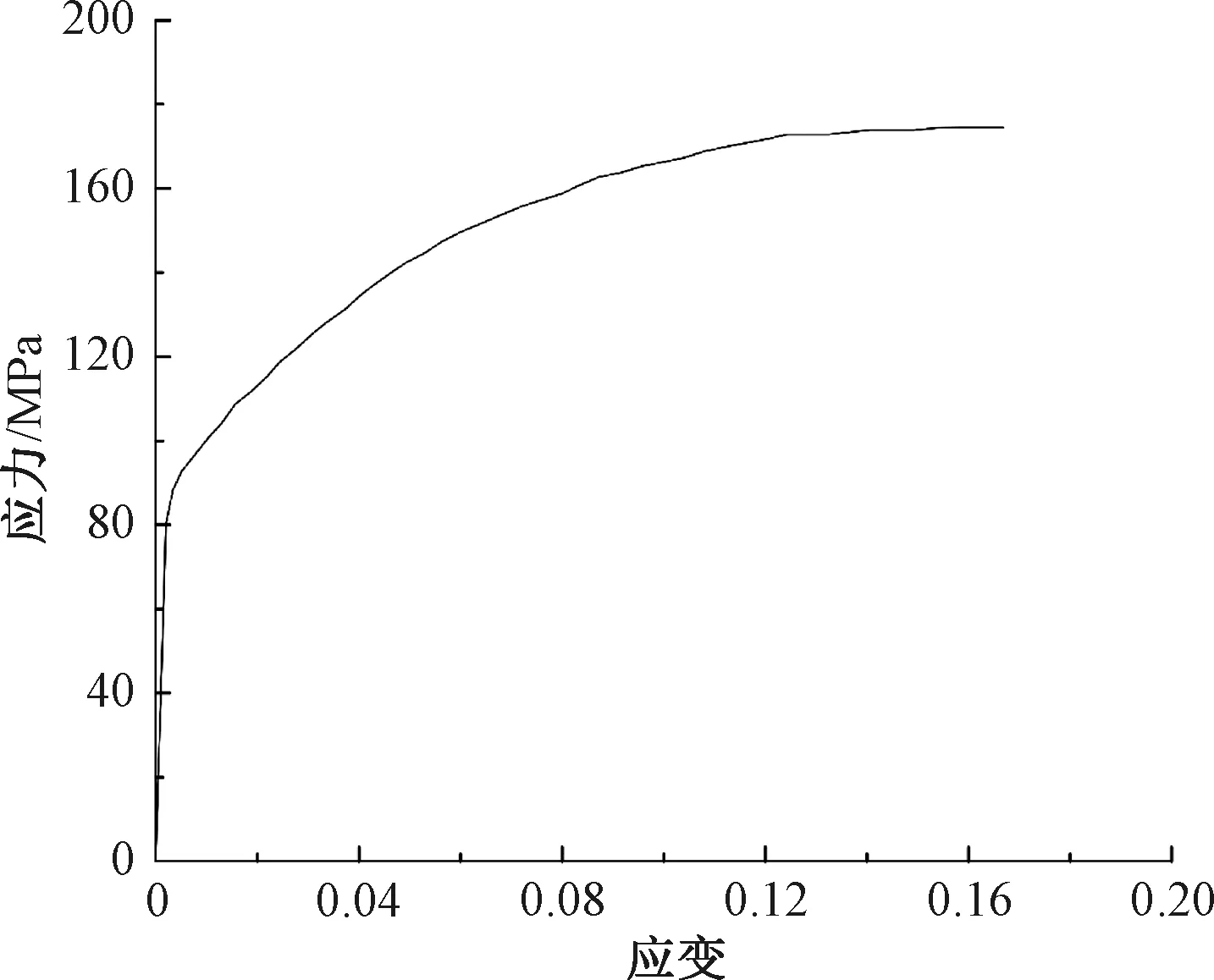
图7 AA6060 T4 的工程应力-应变曲线

为全面反应双面梯度多胞管的耐冲击性能，考虑力学响应指标为

(15)

(16)

(17)

2.3 数值仿真

2.3.1 仿真计算

有限元模型在Ansys/LS-DYNA求解器中进行计算，得到了相应的响应结果。试件的主要力学响应指标统计见表1。每一个试件的最终折叠形态见图8，从图8中可见，所有试件均规律地压溃成手风琴模式，且随着胞元数量的增长，管件的折叠波长逐渐减小，褶皱数明显增多。这意味着胞元的增长可显著提升撞击载荷稳定性。此外，管件的撞击力-压溃距离曲线见图9。

表1 撞击响应的数值仿真结果

图8 试件的最终压溃形态

图9 试件的撞击力-压溃距离曲线

2.3.2 仿真模型验证

为验证仿真模型的可靠性，可将仿真结果与撞击力预测公式进行比对，由于梯度厚度多胞管是一种较新颖的结构，目前尚未有针对这种结构的理论预测模型。因此，将4个均匀厚度多胞管的平均撞击力响应与理论预测方程(式(14))进行对比。根据相关研究，该公式是基于准静态外载荷推导而来，但由于材料的惯性效应和应变率效应，动态载荷作用下的管件平均撞击力要大于式(14)的预测值。Hanssen等[5]通过实验研究提出动态放大系数以修正平均撞击力的理论预测，对于应变率不敏感的铝材料来说，惯性效应是载荷放大效应主因。Langseth等[15]发现，对于无缺陷的AA6060 T4管来说，动态放大系数取值范围为1.3～1.6，而对于有缺陷或诱导结构的管件，这个系数取值将更低。这里将动态系数取值1.3。胞元数为4×4的试件4×4(1.2,1.2)，其截面宽度为90 mm，长度为160 mm，厚度为1.2 mm。通过仿真结果可知其压溃距离系数δ=0.672 。将这些参数代入式(14)，可求得其平均撞击力理论值为80.96×103N。

同样，其他3个均匀厚度多胞管的平均撞击力理论值也可获得，见表2。

表2 均匀厚度多胞管的撞击力响应验证

由表2可见，仿真结果与理论值对应较好。最大误差发生在试件1×1(3.0,3.0)上，与仿真结果相比，其理论预测值减小了5.87%，在可接受范围内。因此，数值仿真模型是可靠的。

2.4 仿真结果分析

2.4.1 胞元密度对管件耐撞性的影响

2.4.2 厚度梯度对管件耐撞性的影响

根据胞元密度的不同，16个试件被分为4组，每组包含4个胞元数量和管件质量均相同的管件。图9(b)～图9 (e)分别呈现了各组试件的撞击力响应曲线。

首先，以胞元数量为2×2的一组试件为例(见图9(c))，随着厚度梯度的增加，加载过程更加稳定，如均匀度厚度试件2×2(2.0,2.0)的响应曲线波动剧烈，当厚度梯度增加至试件2×2(2.6,1.4)的程度，曲线波动已变得相对平缓。这种趋势在其他分组中也能被观察到，尤其在3×3和4×4的分组中，梯度厚度的增加对压溃过程的稳定尤为明显。试件3×3(2.1,0.9)和4×4(1.8,0.6)的曲线平滑程度已近似于蜂窝结构[3]。

其次，增加厚度梯度有效提升了平均撞击力CFE和SEA等响应指标。这种提升在4种胞元密度下均可被观察到。例如在4×4分组中，厚度梯度最大的管件4×4(1.8,0.6)相比于非梯度厚度管件4×4(1.2,1.2)，其平均撞击力、CFE、SEA分别增加了34.4%、32.99%、24.93%。因此，引入双面梯度厚度可以有效提升多胞管的耐撞性能。

3 截面优化

根据上文中的分析，胞元密度和厚度梯度是提升双面梯度管承载能力的两大因素，若要进一步提升吸能效率则需要增大管件的胞元密度或厚度梯度。但根据程耿东等人的研究[8]，当胞元密度超过4×4后，由胞元密度增长带来的吸能效率的增长将逐渐放缓，直到几乎停止，这种趋势王忠刚等人也通过理论分析预测过[9]。

同样，厚度梯度的增长也是有限的，根据双面梯度多胞管的材料分布特征，提升厚度梯度会减小最小厚度t2，当t2过小时，管件有较大几率发生不规则变形使吸能效率降低[13]。因此，需要合理地优化管件截面的材料分布，从而进一步提高管件的吸能效率。

第2节给出的厚度梯度变化方式是较简单的线性变化，这种简单的梯度变化无法拟合到最优材料分布。为使吸能效率进一步提升，这里将以4×4管件为例，对其截面材料分布进行参数优化，使比吸能SEA最大化。

在耐撞性设计中，代理模型优化法是目前结构优化问题的常见方法。本文采用了在多变量输入情况下非线性逼近能力较强、学习速度更快的径向基神经网络法(RBF)来解决这一优化问题。

为了更准确地反应材料分布对响应结果的影响，这里用10个厚度参数来描述4×4管件的截面构型，见图10。这10个参数也在图中被定义。

与前面的仿真分析一样，管件的宽度和长度被分别设定为90、160 mm。10个设计变量的下限和上限均设置为0.6、1.8 mm，因为仿真分析验证了厚度在该范围内的方形多胞管的压溃模式为较为规律的紧凑模式。为尽可能地提高代理模型的精度，同时以较少的样本点数达到要求的精度，减少计算耗时，提高效率，本文采用超拉丁立方采样法，获取合适的样本点。管件压痕诱导槽深度依然是0.6 mm，位置距离管件上端7 mm。有限元建模方法与第2节中相同，用六面体实体单元建模以使响应结果更可靠，且边界条件不变。

优化问题的目标是在轴向冲击下使SEA最大化，SEA值通过式(15)计算。截面构型的差异会导致压溃距离系数δ产生较大的差异，从而影响最终的SEA响应结果。为使每个样本的结果更精确，这里未采用一个统一的压溃距离系数，而是根据每个样本的具体压溃距离系数统计其SEA值。为对比最优样本与第2节中4×4多胞管的吸能效率，给最优样本设定质量约束为不超过457 g，即第2节仿真实验中所有4×4多胞管的质量。优化问题可以通过下式表达

s.t. 0.6 mm≤t1,t2,t3,t4,t5,t6,t7,t8,t9,t10≤1.8 mm

m≤457 g

(19)

图10 双面梯度多胞管截面优化的设计变量

足够的样本点可保证代理模型的精确性，本文以表3中100个样本训练RBF神经网络代理模型，在获得成熟的神经网络后，用剩下的10个样本验证代理模型的拟合精度。运用多学科优化分析软件ISIGHT中的Approximation模块搭建代理模型，将质量m和SEA设为输出响应，拟合方法选择RBF，平滑因子为0，并选择默认最大迭达步数。通过误差分析得到10个检验样本的质量m、SEA输出的平均误差分别为0.69%、4.71%，模型的精度在可接受范围内。将质量约束设定为457 g后，通过全局寻优得到优化后结果见表3，根据最优点的变量值构建有限元模型进行仿真验证，得到的比吸能值也列于表3，该值比代理模型的预测值增加了6.9%，对于一个初步的优化设计，误差在可接受范围。

表3 优化设计样本点和相应的仿真结果

为清晰地展现优化管件对吸能性能的提升，将试件4×4(1.2,1.2)，4×4(1.8,0.6)和优化管件的响应结果进行对比。三者的质量几乎相同，分别为457、457、452 g。通过图11中的响应曲线可以发现，优化管件(4×4(最优))的抗冲击载荷和能量吸收均明显高于其他2个试件。将三者的SEA对比可以发现，4×4(最优)的SEA比恒定厚度管件(4×4(1.2,1.2))增加了35%，比最初的线性变化双面梯度管(4×4(1.8,0.6))增加了8%。在保证了耐撞性能提升的同时，优化管件(4×4(最优))依旧保持了相对稳定的渐进压溃形态。

图11 优化设计样本与其他2个4×4多胞管的响应曲线对比

4 结论

本文研究了具有双面梯度厚度的方形多胞管在轴向撞击下的能量吸收特性。首先基于简化的超折叠单元理论分析了多胞管的3个基本构件(L形，T形和十字形构件)的吸能规律。分析发现，高效吸能区域均集中在翼板交汇处。因此，将一种线性材料分布引入到3个基本构件中，这种分布方式保证了更多的材料集中在高效吸能区。

对4种胞元密度的双面梯度多胞管进行了碰撞仿真分析。分析结果表明，在这4种胞元密度下，梯度厚度设计均可显著提高结构的耐撞性。最大增加由试件4×4(1.8,0.6)贡献，相比均匀厚度管件4×4(1.2,1.2)，其平均撞击力、撞击力效率、吸能效率分别增加了34%、33%、25%。同时，试件4×4(1.8,0.6)仍压溃成稳定的渐进式变形模式。

采用径向基神经网络法对胞元数量为4×4的多胞管进行了初步结构优化，以获得最佳的截面材料分布方式。采用10个厚度变量作为设计变量，优化的目标是使SEA最大化。优化后的管件吸能效率比均匀厚度管件增加了35%，再次验证了双面梯度厚度设计可以有效提高多胞管的吸能效率。