考虑车底和集装箱周转的中欧班列动态服务网络设计研究

兰泽康，何世伟，许 琰

(1. 北京交通大学 综合交通运输大数据运用技术交通运输行业重点实验室，北京 100044；2. 北京工业大学 城市交通学院，北京 100124)

随着“一带一路”相关政策支持和引导，中欧班列发展迅速。2011年至2018年，中欧班列运行线路从1条增长到60多条，班列数量从17列增长到6 300多列[1-2]。中欧班列在快速发展的同时，存在货物运到期限无法保障的问题。我国和欧洲大部分国家铁路的钢轨内距是1 435 mm，而俄罗斯的轨距是1 520 mm，因此中欧班列在出入境和进出欧盟时都需要换装。目前阿拉山口、满洲里、二连浩特3个口岸站都已满负荷运行，拥堵问题造成集装箱口岸滞留时间过长，平均运行时间从刚开通时的15 d增加到现在18～20 d。列车无法按时到达，运到期限无法保障。而相比于海运方式，中欧班列核心竞争力在于其时效性。随着我国产业结构调整，将有更多的高附加值货物选择中欧班列运输。因此，如何更有效地保障货物运到期限是亟需解决的问题。

为减少口岸站集装箱停留时间，需要实现口岸站两端的运行图衔接，并严格按图行车。同时为每支货流制定全程挂线车次，有利于货流的运到期限追踪与预警。而中欧班列采用规划型运输组织模式，每月排定下个月各地班期[3]，班列的正点发车率会作为铁路部门的重要考核指标，这为按图行车创造了良好条件。铁路货运动态服务网络设计属于战术层面的规划内容，是指在一定时间精度内(如1 h)，确定所需要建立的运行线和货流挂线方案。与传统的货运服务网络设计[4]相比，动态服务网络设计的引入了时间维度，一个重要的输入数据为每支货流的到达时间，反映了其动态属性，所确定的运行线等结果可以为编制运行图奠定基础[5-6]。为此，本文展开对中欧班列动态服务网络设计的研究。

在中欧班列运输组织方面已有相关研究。文献[7]提出以乌鲁木齐为中欧铁路货运集拼中心，以运营者总利润最大为优化目标，构建以发车频次为决策变量的模型；文献[8]针对当前中欧班列点对点直达班列货源规模不足的问题，以提高班列运行时效性和稳定性为目标，建立网络化列车开行方案的混合整数规划模型；文献[9]利用复杂网络理论从国内27个候选城市中确定10个集结中心，并建立去程方向给定列车开行频率的配流模型；文献[10]分析了直达与集结两种运输组织模式的利弊，构建去程班列运输组织方案的优化模型，可计算出最优的运输组织模式。可见，目前针对中欧班列研究大多限于静态货流，且很少考虑班列在口岸站的换装作业，大多只研究去程方向的运输组织，缺少双向协同组织的研究。

在考虑相关设备资源利用的动态服务网络设计方面，既有研究大多通过建立离散时空网络，再基于多商品网络流模型构建数学规划模型。文献[6]建立混合整数规划模型以同时解决列车开行时段、编组内容和车辆周转等问题；文献[11-12]通过建立周期性的时空网络描述车底周转以及货流分配，均构建了基于车底时空路径的混合整数规划模型，采用列生成算法生成相应的时空路径；文献[13]进一步考虑了跨国境时机车换挂问题；文献[14]考虑运输方式选择，建立运输方式-时间-空间三维网络描述装备资源周转，具体到装卸过程。文献[9-11]研究车底周转时，车底运用方式均为不固定区段，造成车底可能周转的方案数量巨大，模型求解困难。在资源利用方面，现有研究仅涉及到一种资源(车底或装备资源)的周转。

本文基于给定的中欧班列轴辐式网络(Hub-and-spoke)结构，研究其动态服务网络设计问题，并考虑固定区段的车底周转和集装箱周转，使其发挥最大效力，避免由于动力资源(车底)和装备资源(集装箱)的不足使得计划无法实现。构建以最小化车底运用费用、货流运输费用、货流停留费用和空箱运输费用为目标的混合整数规划模型，实现货流、箱流、列流的综合优化。

1 问题描述

1.1 中欧班列运输组织过程

目前中欧班列采取“点对点”的直达运输组织模式，即在某一城市集结周边同去向货源，并以该城市为始发地往另一地区某城市开行集装箱直达班列[10]。但由于中欧班列在经过口岸站时需要进行换装作业，即将到达口岸站的列车(车底)上所有集装箱调运放置到另一列车上，车底资源往往仅限于某一地区内运行。货流在源点用集装箱空箱装箱后，通过一列或多列列车运送至终点，中途运输过程不需要拆箱。中欧班列运输组织过程示意见图1。

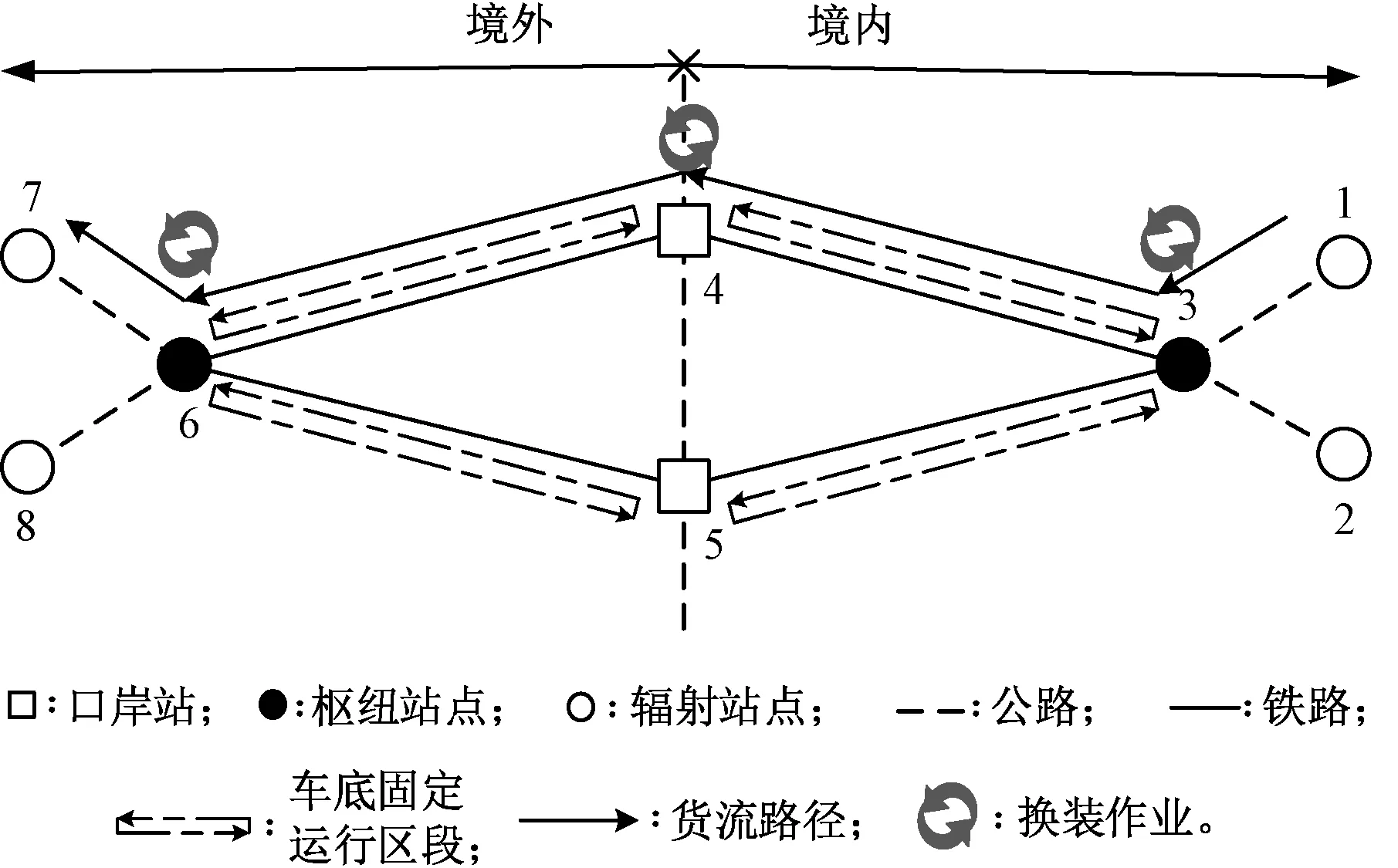
图1 中欧班列运输组织过程示意

现以图1中一支去程方向的货流运输组织过程为例，说明中欧班列的运输组织过程。图中各站点类型已给定，例如站点1为辐射点(Spoke)，站点3为枢纽站点(Hub)，站点4为口岸站，区段线路类型也已给定，例如区段1—3为公路，区段3—4为铁路，且所有区段均为双线。铁路通道的每个区段内存在列车车底往返运输集装箱重箱和空箱，而公路区段用卡车装运集装箱。一支货流需从站点1运送至站点7，给定其运输物理路径为1→3→4→6→7，即货流在始发站点1用空箱装箱后，通过公路运输在站点3集结，再通过铁路通道运输至枢纽站点6，最后通过公路疏运至站点7，在站点7拆箱完成交货。图1中的货流整个运输过程中存在3次的换装作业，分别为在站点3由公路中转至铁路，在站点4由区段3—4的车底换装至区段4—6的车底上，以及在站点6由铁路中转至公路。

1.2 基于离散时空网络的问题描述

1.2.1 离散时空网络构建

给定中欧班列运输物理网络G=(N,E)，其中：N为所有节点(即站点)集合，i,j∈N；E为所有弧段(即两相邻站点之间有向运输线路)集合，e∈E。le为e的里程，km；oe、de分别为弧段e的起点和终点，oe,de∈N；B为所有区段集合，每个区段b∈B包含两个反向弧段b1∈B和b2∈B，b1和b2里程相同，例如图1中区段3—4包含弧段3→4和弧段4→3。ERail为所有铁路弧段集合；BRail为所有铁路区段集合，BRail⊂B，任意b∈BRail包含两个反向铁路弧段，即b1,b2∈ERail。

如现有关于动态货运服务网络设计文献[11-13]，假设货流以一定的周期(如1个月)呈现，以该周期作为规划时长，记为Tmax，h。对规划时段以单位时长τ离散化，T为所有时间段索引集合，T={0,1,2,…,(Tmax-τ)/τ}，例如第0个时间段表示时间段[0,τ)。

截取图1中部分物理网络，其对应离散时空网络见图2，假设Tmax=10，τ=1。由图2可知，区段1—3运输需要1个时段，区段3—4运输需要2个时间段。规划时段具有周期性，例如弧段3—4第9个时段出发的运行线，于下一规划阶段的第1时段(〈9+2〉=11mod10=1)到达站点4。

图2 离散时空网络示意

1.2.2 货流运输的时空网络描述

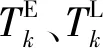
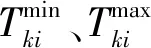
(1)

(2)

的所有解即为所有可能的停站方案。

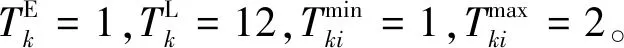
1.2.3 车底周转的时空网络描述

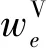
图3 车底周转时空网络

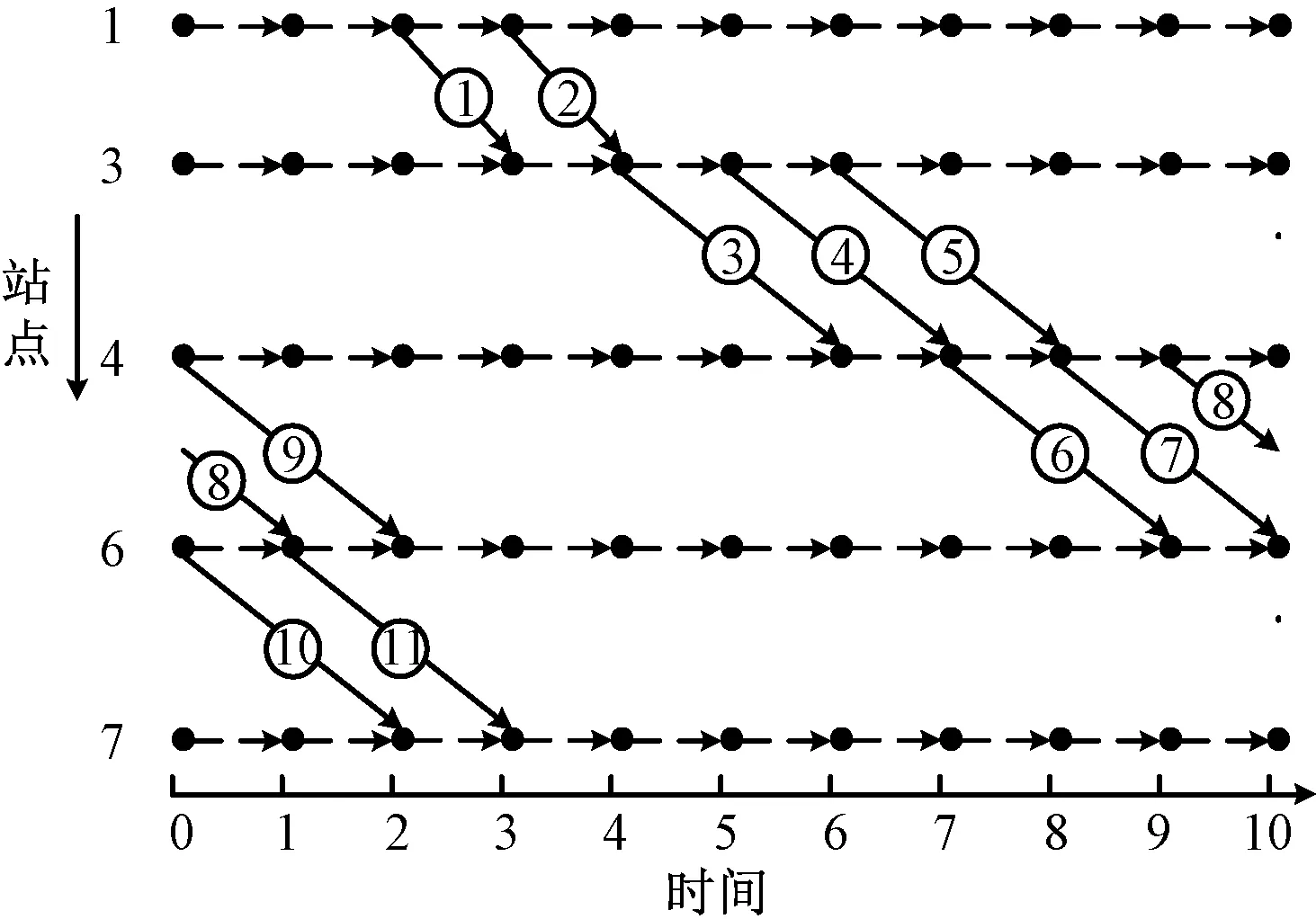
图4 货流运输时空网络

1.2.4 研究目标

基于所建立的离散时空网络，研究需要给出列车开行时段(即所需建立的运行线)，车底周转方案，集装箱周转方案和货流挂线方案。研究的目标是最小化总运营费用，包括车底运用费用，货流运输费用，货流停留费用和空箱运输费用。

2 模型建立

2.1 决策变量

决策变量及定义见表1。

表1 决策变量及定义

2.2 模型建立

建立综合列车开行时段选择、车底周转、集装箱周转和货流挂线方案的优化模型。

(1)目标函数

(3)

目标函数式(3)表示最小化总运营支出，包括车底固定费用、车底运行费用、货流运输费用、货流停留费用、集装箱空箱运输费用和货流被取消的惩罚费用。

(2)车底周转约束

(4)

(5)

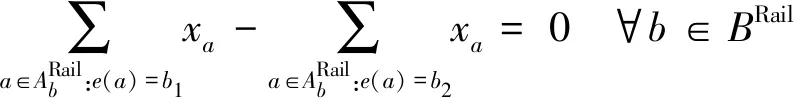
(6)

式(4)表示若运行线a∈ARail被选择，则运行线a为车底开始任务或者有且仅有一个接续对(l,a)∈EV被选择；同理，式(5)表示若运行线a∈ARail被选择，则运行线a为车底结束任务或有且仅有一个接续对(a,l)∈EV被选择；式(6)表示对于任意区段b∈BRail，b1方向被选择的运行线数量等于b2方向被选择的运行线数量，即两相反方向被选择的运行线数量相等，该约束保证了规划结束时，每个站点保留的能运行于相应区段的车底数量不发生变化。现证明该约束可以保障车底守恒：车底执行的任务数量是奇数或者偶数。由于担当偶数次任务的车底总是回到始发站点，且这部分任务恰好满足两相反方向的任务数量相等。因此，可以不考虑执行偶次数任务的车底，只需考虑执行奇次数任务的车底(这些车底从区段一个端点始发，在区段的另一个端点终到)。若要满足车底数量守恒，则从区段两端点出发的执行奇次数的车底数量应相等，从而区段内两相反方向被选择的运行线数量相等。若区段内两相反方向被选择的运行线数量不相等，则可以反推得车底不守恒。例如图4中区段3—4和4—6内被选择的运行线数量是相等的，故而车底不需要空驶，每个周期内可以周而复始使用车底。

(3)货流平衡约束

(7)

式(7)表示对于任意货流k∈K，货流在所有时空路径Pk上的货流量与取消的货流yk之和等于货流量大小μk。

(4)运行线能力约束

(8)

(9)

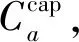
(5)货流挂线方案数量限制约束

fkp≤μkzkp∀k∈Kp∈Pk

(10)

zkp≤fkp∀k∈Kp∈Pk

(11)

(12)

式(10)表示若fkp≥1，则zkp=1；式(11)表示若zkp=1，则fkp≥1；式(12)表示货流最多能选择挂线方案数量约束。

(6)集装箱周转约束

qa≥0 ∀i∈Nt∈T

(13)

(14)

式(13)表示任意站点任意时刻的集装箱供给能力约束；式(14)表示在规划时段内，任意站点发送的集装箱数量等于到达的集装箱数量，保证了集装箱数量的守恒。

(7)变量取值范围约束

(15)

xal∈{0,1} ∀(a,l)∈EV

(16)

yk,fkp≥0且为整数 ∀k∈Kp∈Pk

(17)

qa≥0且为整数 ∀a∈AS

(18)

3 算例分析

3.1 基础数据和参数设置

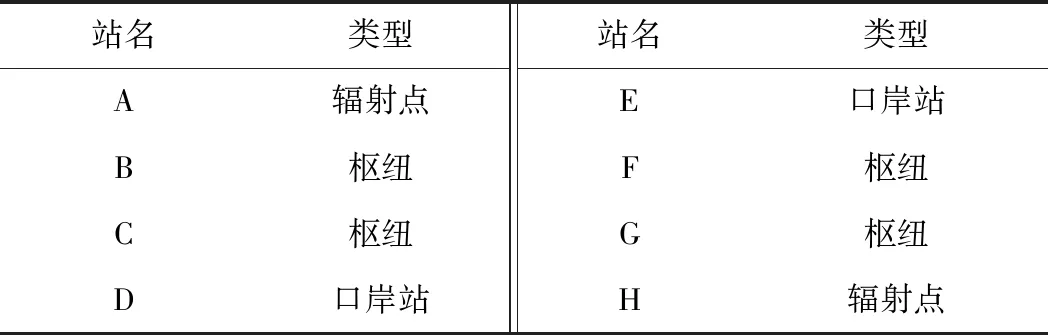
表2 站点信息

表3 区段信息

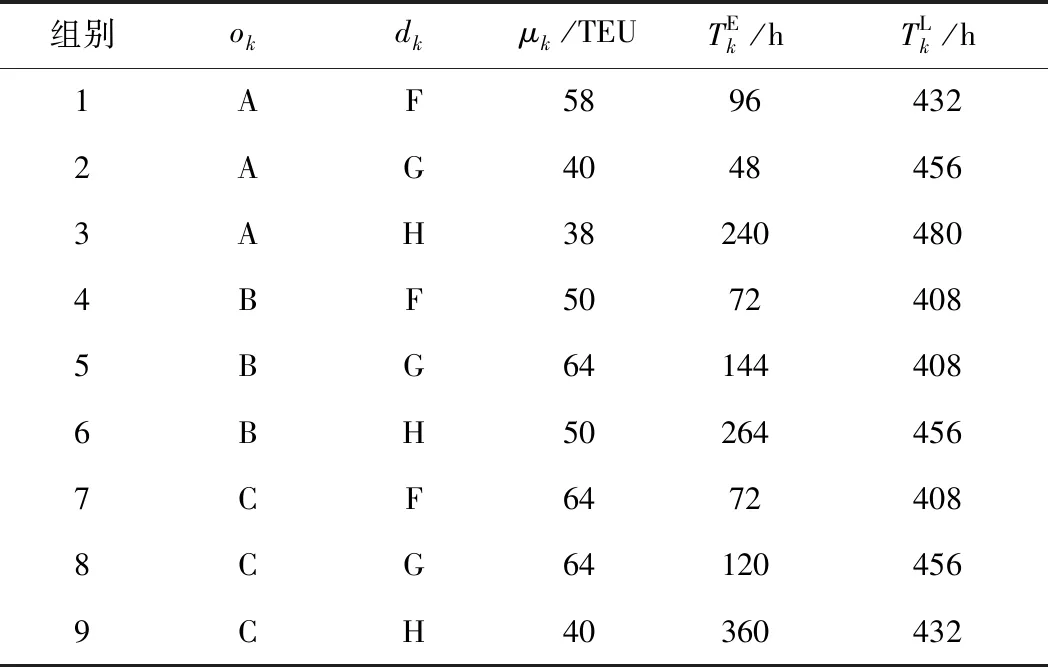
表4 部分货流信息

表5 模型参数取值

图5 算例物理网络

在Visual Studio 2015平台上用C#编程调用GUROBI 8.1.0的.NET的API接口求解模型，测试计算机为一台配置Intel Core i5-8300H CPU, 2.30 GHz和12 GB内存的笔记本电脑。模型求解的终止条件设置为求解时长达到1 h，或者上界和下界的间隔Ggap不大于0.5%。

3.2 求解结果

设计5个不同规模大小的案例1见表6，从案例1到案例5，货流和网络节点数目递增，求解规模递增。求解结果(所有求解结果不存在被取消的货流)见表7。可以看出，所有案例在1 h内均能求解得到质量较好的解。其中案例5列车开行时段见图6，图中同一铁路区段内同种颜色的运行线表示一个车底在规划周期内的执行任务轨迹，如图中为突出显示而加粗的两条轨迹所示。

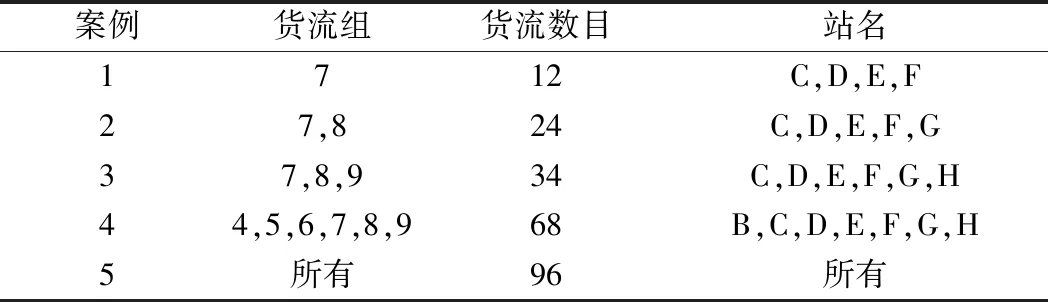
表6 案例参数

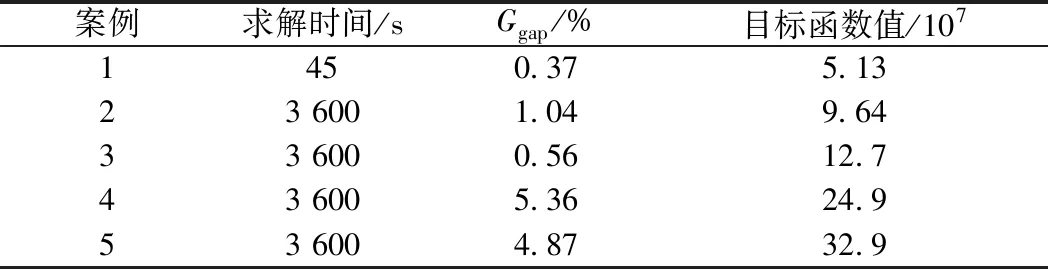
表7 案例求解时间和目标函数值

现分析考虑车底周转、集装箱周转和限制货流挂线方案数量对模型求解效率的影响。当考虑所有约束条件时，记为“S1”;当不考虑车底周转约束式(4)～式(6)时，记为“S2”;当不考虑集装箱周转约束式(13)～式(14)时，记为“S3”;当不考虑货流挂线方案数量限制约束式(10)～式(12)时，记为“S4”。针对案例5、4种情形求解的迭代收敛曲线见图7。由图7可知，车底周转约束对模型求解效率的影响最大，其次为货流挂线方案数量限制约束，而集装箱周转约束影响最小。

以案例5为例分析τ在不同取值时对模型求解效率的影响，见表8。可见，随着τ的减小，即离散时间间隔越小，货流的可能选择的时空路径数量逐渐递增，求解的难度也越来越大。在1 h内，最终的Ggap值越来越大，当τ=4时，模型在1 h内，无法找到可行解。同时发现越小的τ值，终止时目标下界值越小，因为τ值越小意味着搜索的解空间越大，求解的结果越精细，可能搜索到更优的解。

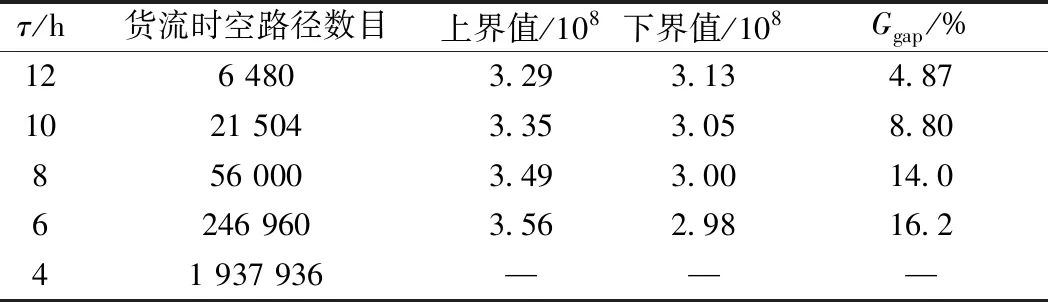
表8 案例5在τ不同取值时的求解结果

4 结束语

本文针对目前中欧班列运到期限无法保障的问题，研究其动态服务网络设计方法，实现流线耦合优化，同时考虑固定区段的车底周转和集装箱周转，为运输计划的执行提供相应的资源保障。论文研究成果对于中欧班列的运行组织具有一定的借鉴意义。需要指出，货流量大小以及其最早提货时间等在实施日中有所变动，如何编制更具有鲁棒性的运行计划，如超售和延迟策略，将是下一步研究的重点方向。