应用动力吸振器的浮置板轨道低频振动控制特性的试验研究

朱胜阳，王建伟,2，蔡成标，杨吉忠，杨尚福

(1. 西南交通大学 牵引动力国家重点实验室，四川 成都 610031；2. 北京城建设计发展集团股份有限公司，北京 100037;3. 中铁二院工程集团有限责任公司，四川 成都 610031)

本文基于多自由度系统等价质量识别法和扩展定点理论[13]，以实验室铺设的短型钢弹簧浮置板轨道的参数为基础，结合浮置板轨道模态分析与测试，首先设计确定了动力吸振器的最优设计参数，在综合考虑动力吸振器安装方式、位置以及制作材料等众多因素的前提下，设计了合理的动力吸振器装置，然后将制作好的动力吸振器安装在室内实尺浮置板轨道上，采用自主设计研发的落轴小车进行落轴冲击动力学试验，研究应用动力吸振器的浮置板轨道在落轴冲击载荷作用下的低频振动特性，研究结果为解决浮置板轨道低频振动控制问题提供了重要的参考。

1 动力吸振器设计

1.1 动力吸振器设计原理及方法

文献[13]详细介绍了基于单自由度系统的扩展定点理论。浮置板轨道是一个具有多阶振动模态的连续体系，本文将基于模态分析技术，利用模态向量的正交性将浮置板轨道连续系统离散成由多个单自由度组成的非耦合系统，根据单自由度系统的制振设计方法设计合理的动力吸振器参数，从而达到控制浮置板系统低频振动的目的。图1为在实验室实尺浮置板轨道上附加动力吸振器的示意图。

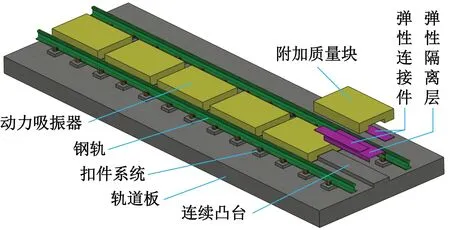
图1 应用动力吸振器的轨道板示意图

根据多自由度系统等价质量识别原理，轨道板第i阶模态的等价质量Mi与等价刚度Ki分别为

(1)

(2)

式中：Ei为轨道板第i阶模态对应的总动能;ωi为轨道板的第i阶固有频率。

根据扩展定点理论[13]可知，控制浮置板轨道不同阶模态的动力吸振器最优设计参数为

mi=μiMi

(3)

(4)

(5)

式中：μi为动力吸振器与浮置板轨道的质量比;mi、ki和ci分别为动力吸振器的质量、最优设计刚度和最优设计阻尼;Zi和ζi分别为浮置板轨道和动力吸振器第i阶模态的等效阻尼比。

由式(3)～式(5)可知，在设计动力吸振器的过程中，只要确定了动力吸振器与浮置板轨道的质量比μi，就可以求解出动力吸振器的质量与最优设计阻尼。在确定动力吸振器的最优设计刚度时，可先求出动力吸振器在浮置板轨道第i阶模态的等效阻尼比Zi=0时的最优设计刚度，然后遵循最优同调原则，对其进行适当修正从而获得其最优值。

1.2 浮置板轨道现场测试及模态仿真分析

动力吸振器的设计以浮置板轨道的模态振型为基础来进行，因此首先需要确定浮置板轨道的低阶模态振型及其对应的固有频率。本文通过实尺浮置板轨道的模态测试与模态仿真分析，确定浮置板轨道的固有频率等关键参数。

实验室实尺浮置板轨道长9.06 m、宽3.15 m、厚0.495 m，支承层宽3.6 m、厚0.26 m，两根钢轨之间无凸台结构。根据实验室实尺寸浮置板轨道参数，采用Ansys软件建立三维有限元模型，见图2，并对其进行模态仿真分析。钢轨采用梁单元模拟，两端施加简支约束；轨道板、支承层与路基分别采用实体单元模拟，其中支承层与路基两端对称约束，地基侧面和底部分别建立等效黏弹性边界单元[14]，并将其最外层节点固定约束；扣件系统和钢弹簧隔振器采用弹簧-阻尼单元模拟[15]。浮置板轨道相关参数见表1。

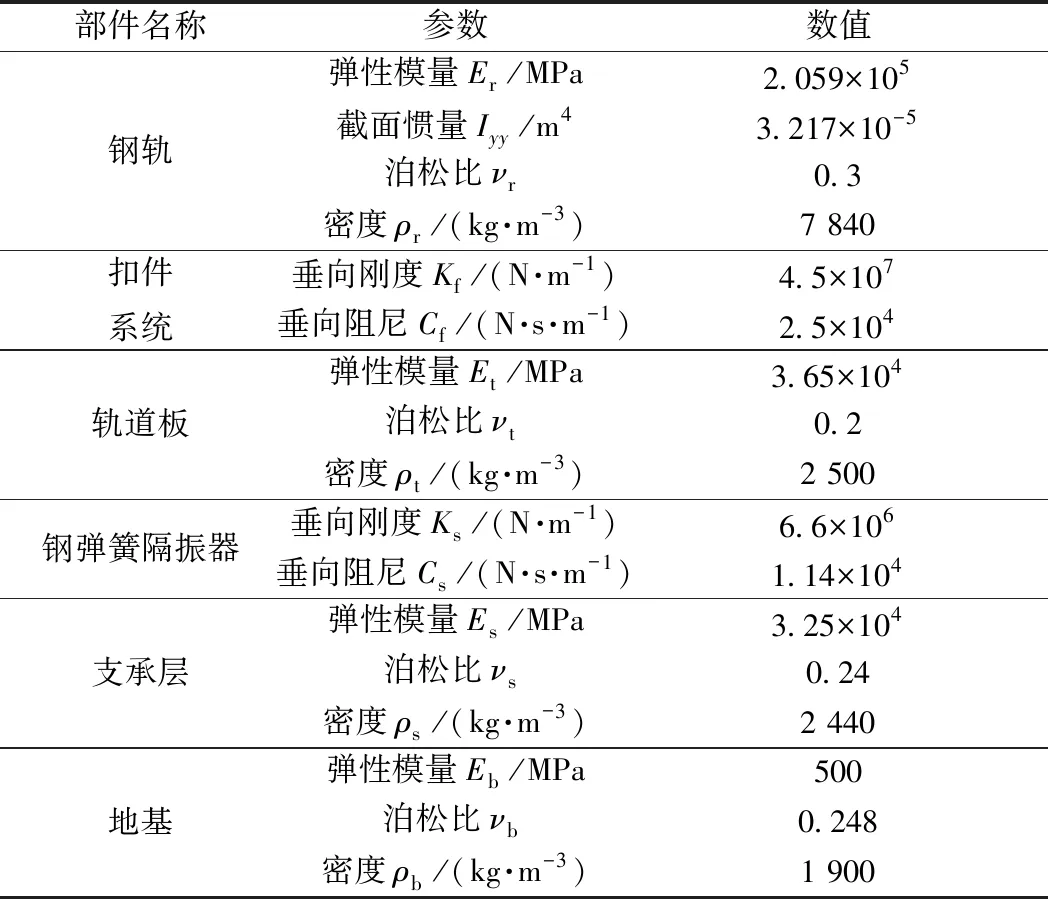
表1 浮置板轨道参数

为了保证计算参数的准确性与分析结果的可靠性，本文对实验室浮置板轨道进行了模态测试，从而对浮置板轨道有限元模型进行修正与验证。本次试验选取德国M+P公司的VibPilot动态测试软件作为数据采集系统。在进行模态测试时，采用力锤依次在轨道板不同位置处进行锤击，通过安装在浮置板轨道上的传感器采集轨道板的振动响应，并采用M+P SmartOffice 分析软件(V4.4)对采集到的数据进行模态分析。为了保证浮置板轨道有限元模型的准确性与可靠性，本文将模态测试结果与模态仿真分析结果进行了对比，并对有限元模型的计算参数进行了验证与修正。

浮置板轨道模态测试与仿真的结果及其偏差见表2，对应的模态振型见图3、图4。其中，第1阶模态以轨道板的垂向平动为主，第2阶模态与第3阶模态以绕轨道板中心线的转动为主，第4阶模态以轨道板的一阶垂向弯曲为主。

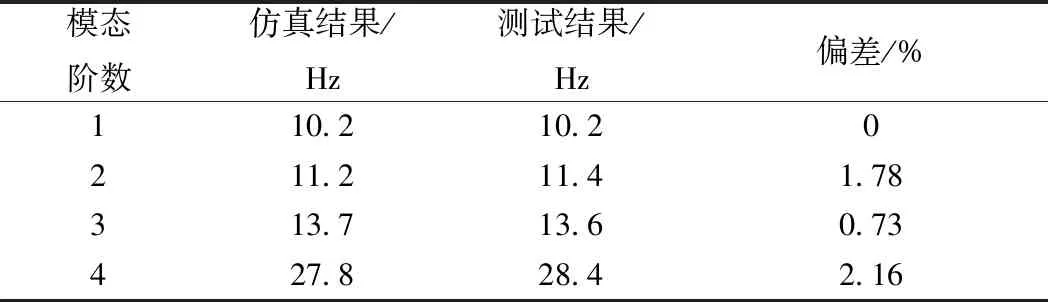
表2 浮置板轨道模态分析结果与现场模态测试结果对比

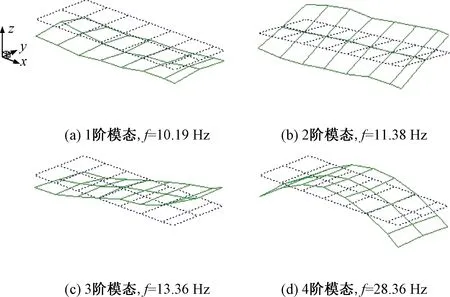
图3 浮置板轨道模态测试结果

由表2结果可知，浮置板轨道现场模态测试与有限元模态分析的结果偏差在±3%以内，且由图3及图4的模态振型可知，二者具有较好的一致性，表明所建立的浮置板轨道有限元模型具有较高的准确性与可靠性，并且通过仿真测试确定了浮置板轨道的前4阶固有频率与模态振型。

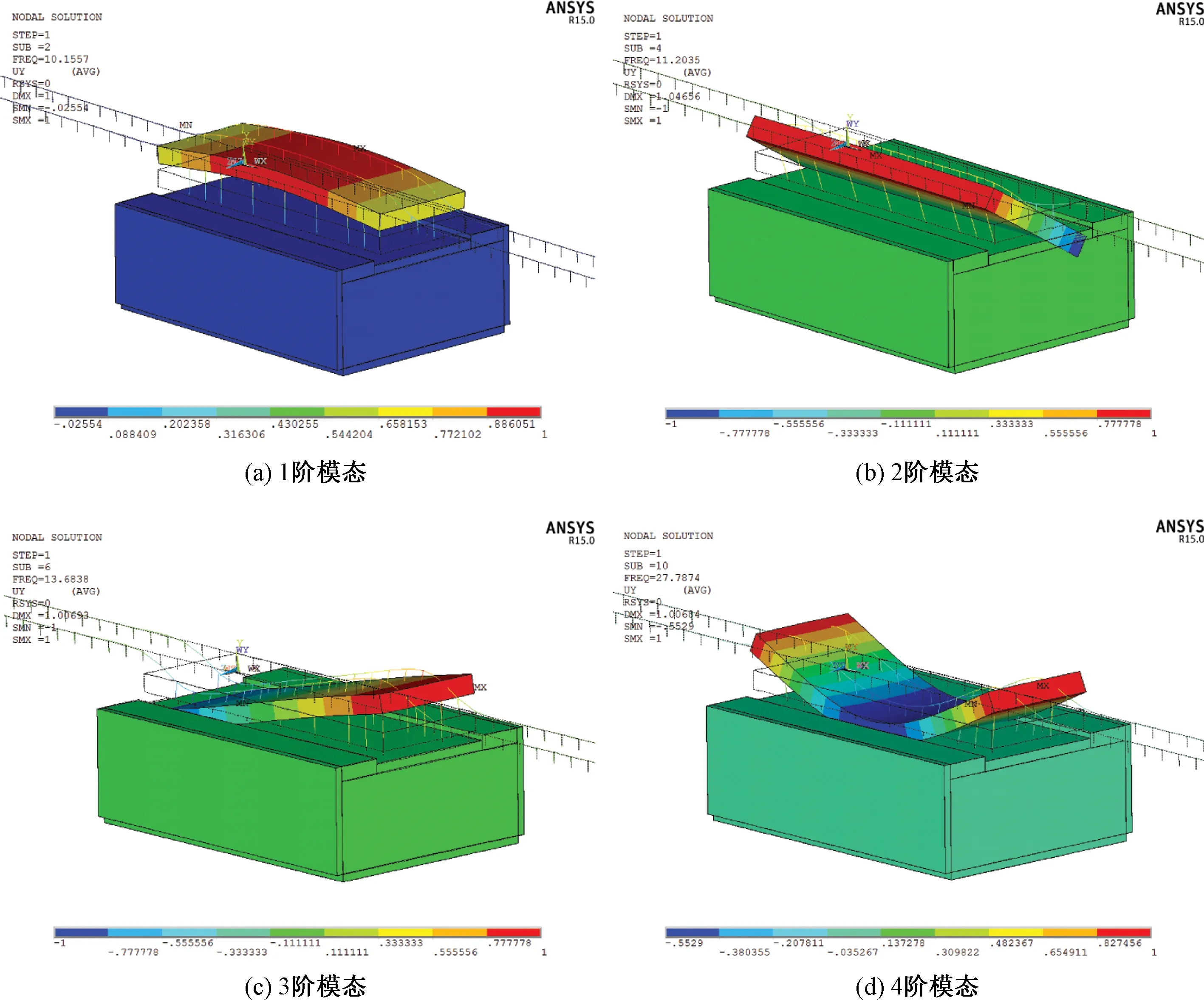
图4 浮置板轨道模态分析结果

1.3 动力吸振器设计参数

由于浮置板轨道主要在第1阶固有频率处产生低频域内的振动放大现象，所以本文主要控制浮置板轨道的第1阶模态振动，从而抑制浮置板轨道产生的垂向振动。根据式(1)、式(2)，并结合浮置板轨道模态分析与测试的结果，可得轨道板第1阶模态的等价质量、刚度分别为33 400 kg、149.97 kN/mm。本文选定动力吸振器与浮置板轨道的质量比分别为0.1、0.2、0.3，则抑制浮置板轨道第1阶模态振动的动力吸振器最优刚度及阻尼可按式 (3)～式(5)计算得到。

通过模态测试与有限元分析可知，浮置板轨道的第1阶模态振型以轨道板的垂向平动为主，因此动力吸振器质量块的集中安装与离散安装方式不会对浮置板轨道第1阶振型产生明显影响。为了方便动力吸振器装置的制作与安装，本文采用集中质量块离散化的方式，将其均匀布置在浮置板轨道的纵向中心线上。根据不同质量比计算得到的动力吸振器的最优参数见表3。

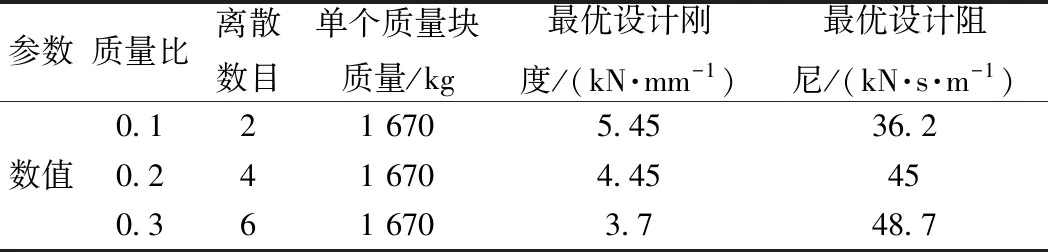
表3 动力吸振器的最优设计参数

图5给出了不同工况下浮置板谐响应幅频曲线，在计算分析中，采用Mass21质量单元模拟动力吸振器的附加质量块，采用Combin14弹簧-阻尼单元模拟弹性连接件，且在钢轨上施加大小为15 kN、激振频率范围为0～20 Hz的简谐荷载。

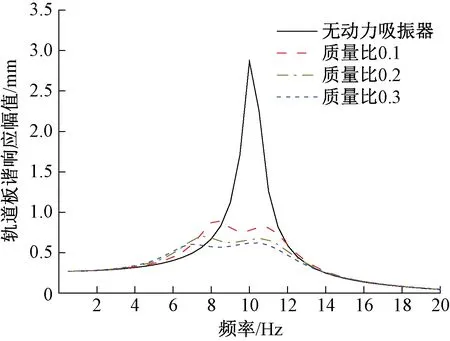
图5 不同工况下轨道板谐响应幅频曲线

由图5可知，在最优设计参数下，动力吸振器能够明显抑制浮置板轨道固有频率处的振动位移峰值，且质量比越大，效果越明显。

2 应用动力吸振器的浮置板轨道落轴试验

2.1 动力吸振器装置的制作与安装

动力吸振器装置主要由附加质量块与弹性连接件组成。

(1)质量块

实验室实尺浮置板轨道的外部尺寸如下：板长9.06 m，板宽3.15 m，板厚0.495 m，且两根钢轨之间无任何凸起，因此可将动力吸振器安装在两根钢轨之间。综合考虑钢轨间有限的安装空间、质量块的制作周期以及维护等因素，本次试验选取密度较大的钢材制作动力吸振器的质量块。

(2)弹性连接件

弹性连接件作为连接动力吸振器与轨道板的主要部件，其刚度与阻尼特性直接影响动力吸振器的振动控制效果。由表3可知，动力吸振器在不同质量比下的最优刚度与阻尼表现出“阻尼大则刚度小”的特点，但是制作同时满足大阻尼、小刚度的弹性连接件是比较困难的。经过大量的试验，最终确定安装在浮置板轨道上的动力吸振器弹性连接件的刚度为7.52 kN/mm，是最优刚度值的两倍；其阻尼为49.8 kN·s/m，满足质量比0.3时的最优参数要求。

根据以上要求，制作动力吸振器装置，并将其安装在浮置板轨道上，见图6。

图6 动力吸振器装置的安装

2.2 落轴试验方案

落轴试验在西南交通大学轨道交通实验室浮置板轨道试验平台上进行，落轴试验装置见图7。试验时，首先通过遥控装置将落轴试验车运行至落轴位置，然后将落轴试验车顶升，与钢轨脱离接触，并通过轮对自动对中装置将轮对中心与轨道中心线对齐，再通过电磁铁将轮对提升至落轴试验高度，最后控制电磁铁断电，将轮对自由落下以对浮置板轨道施加冲击载荷。

图7 落轴试验车

测试断面位于浮置板轨道板中与板端位置，并在附加质量块、轨道板、支承层等布置测点，见图8。由于本文仅考虑动力吸振器对浮置板轨道垂向振动的控制作用，因此传感器仅布置竖向。

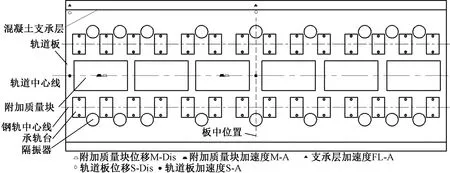
图8 动力吸振器质量比0.3工况下测点布置

数据采集设备选用德国IMC型32通道高精度数据采集仪，选取量程50g，灵敏度100 mV/g的DYTRAN3 145 A型压电式加速度传感器安装在轨道板与附加质量块上进行加速度测量；选取量程5g，灵敏度1 000 mV/g的DYTRAN3 192 A型压电式加速度传感器安装在混凝土支承层上进行加速度测量；选取量程±10 mm，灵敏度0.5 V/mm的NS-WY02位移传感器安装在轨道板与附加质量块上进行位移测量。

为减少浮置板轨道纵向边界效应的影响，将落轴点设置在轨道板的板中截面。落轴高度决定浮置板轨道动态响应的大小，为了充分激发轨道各部分的振动，本试验的落轴高度为20 mm，并进行多次试验。

本次试验共设计了4种工况，工况1为无动力吸振器的浮置板轨道工况，工况2～4为应用质量比分别为0.1、0.2、0.3的动力吸振器的浮置板轨道工况，其中，工况1作为工况2～4的对比工况。

2.3 低频振动效果评价方法

(1)振动加速度级

GB 10071—1988《城市区域环境振动测量方法》规定[16]，振动加速度级VAL的表达式为

(6)

式中:arms为加速度有效值;a0为基准加速度，一般取为10-6m/s2。

三分之一倍频程各中心频率的振动加速度级可采用频率计权因子修正后得到，称为分频振级，其可反映某一频段内振动水平，其中，频率计权因子参考GB/T 1344.1—2007《机械振动与冲击 人体暴露于全身振动的评价 第1部分：一般要求》[17]。

(2)插入损失

插入损失常用于评价结构的减隔振效果。在浮置板轨道上应用动力吸振器前后轨道系统的插入损失eIL为

(7)

式中：awith为应用动力吸振器后浮置板轨道的加速度有效值；awithout为无动力吸振器时浮置板轨道的加速度有效值。

若eIL>0，表明应用动力吸振器后浮置板轨道的振动有所减小，动力吸振器起到了控制振动的效果；若eIL<0，表明应用动力吸振器后浮置板轨道的振动不但没有减小，反而在一定程度上有所增加。

3 试验结果分析

本文主要关注应用动力吸振器的浮置板轨道在低频域内的振动控制特性，因此以分析4～32 Hz较低频率范围内的振动为主。应用质量比分别为0.1、0.2和0.3的动力吸振器后，轨道板与支承层在浮置板轨道板中位置处的加速度幅频曲线，并与未采用动力吸振器的工况进行了对比，见图9。

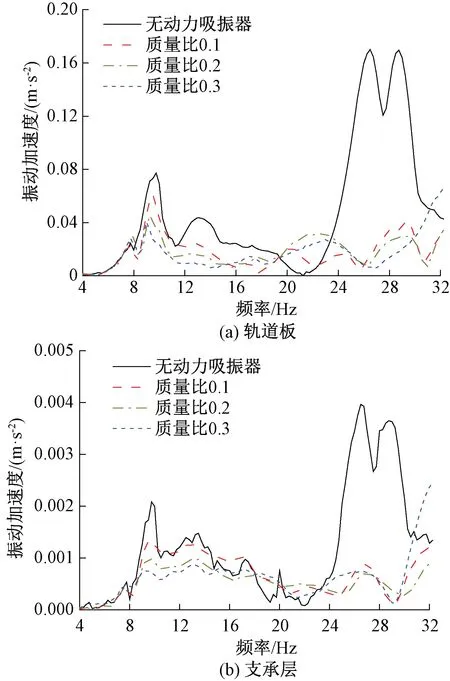
图9 不同工况下轨道板、支承层加速度频域幅值

由图9可知，在落轴冲击载荷作用下，无动力吸振器装置的浮置板轨道加速度在频率10、13、25～30 Hz等处出现较大的峰值。由1.2节分析结果可知，浮置板在频率为10 Hz时表现为垂向平动模态，在频率为13 Hz时表现为刚体转动模态，在25～30 Hz的频率范围内表现为一阶垂向弯曲模态。由图9(a)可见，在这些频率处均出现了明显的峰值，表明轮对冲击载荷激发了这些频率所对应的模态；在浮置板轨道上应用不同质量比动力吸振器后，上述频率附近特别是在25～30 Hz的频率范围内，轨道板和支承层的加速度均得到了明显抑制，且振动抑制效果随动力吸振器质量比的增加越来越明显，进一步表明了动力吸振器对浮置板轨道的共振峰值有良好的抑制作用。以轨道板为例，在未安装动力吸振器的情况下，浮置板轨道在10、13、25～30 Hz频率处的振动加速度峰值分别为0.077、0.044、0.170 m/s2，当应用质量比为0.3的动力吸振器后，浮置板轨道在上述频率处的振动加速度峰值分别降至0.040、0.008、0.029 m/s2，降幅分别为48.1%、81.8%、82.9%。落轴冲击荷载下轨道板的时域响应见图10。由图10可知，附有动力吸振器的浮置板轨道板中位置处的加速度峰值减小了11 m/s2左右，振动控制效果较为明显。

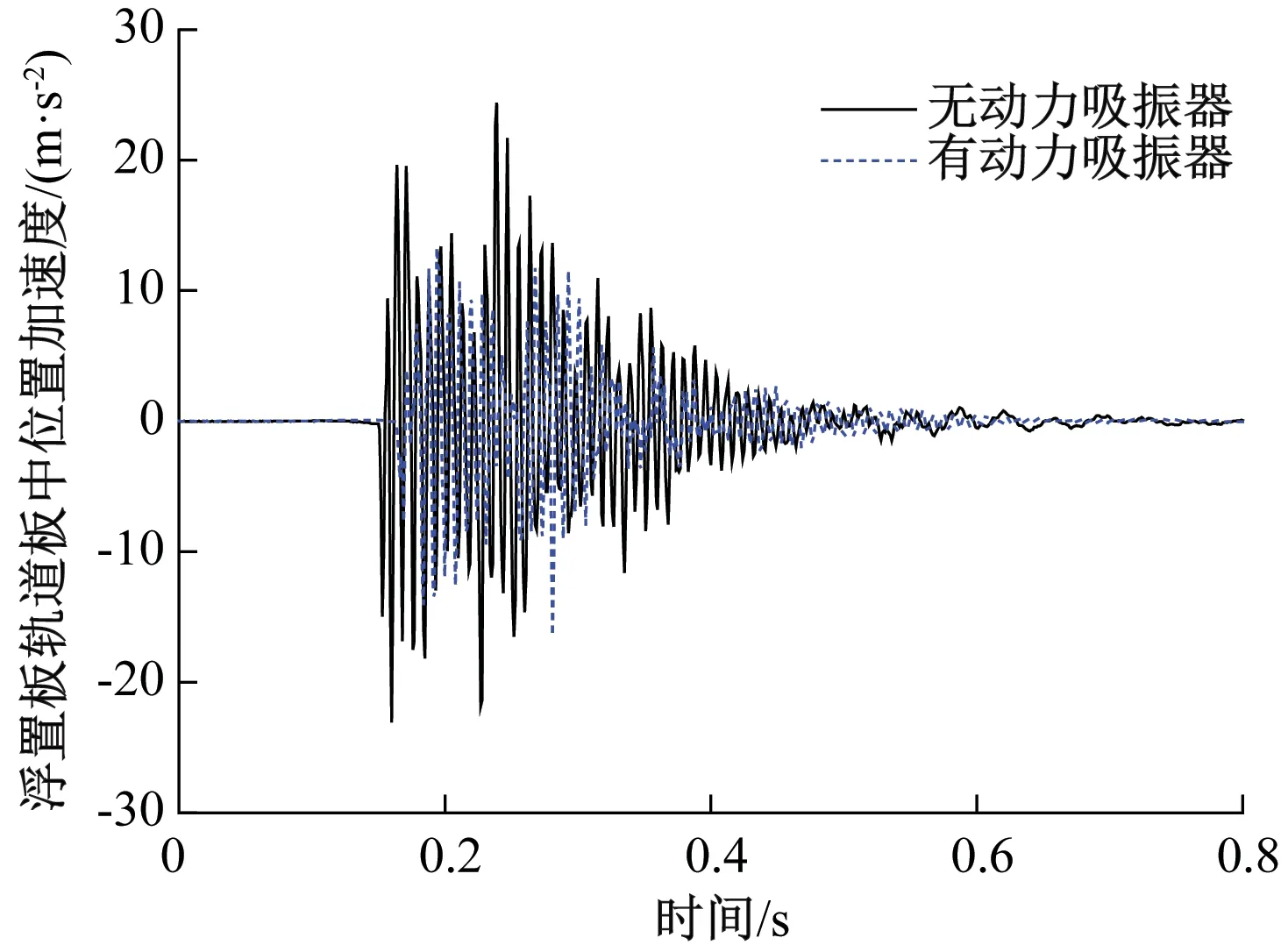
图10 有无动力吸振器工况的轨道板加速度

根据2.3节定义，分别计算不同工况下浮置板轨道1/3倍频程下振动加速度分频振级，并计算对应的插入损失，其中频率分析范围为4～32 Hz。不同工况下轨道板和支承层的振动加速度分频振级与插入损失见图11～图12。

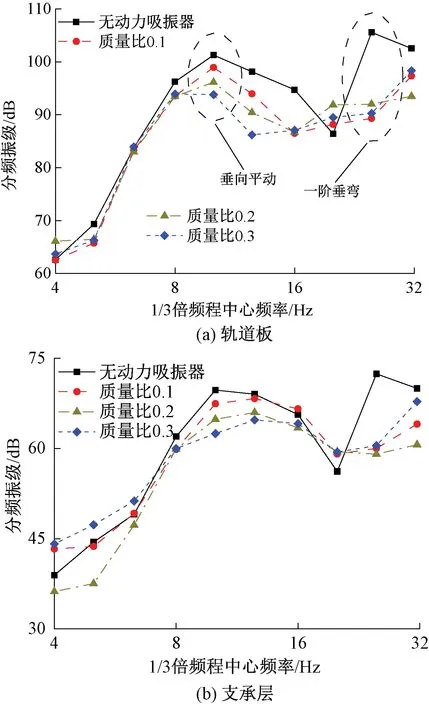
图11 不同工况下轨道板、支承层振动加速度分频振级

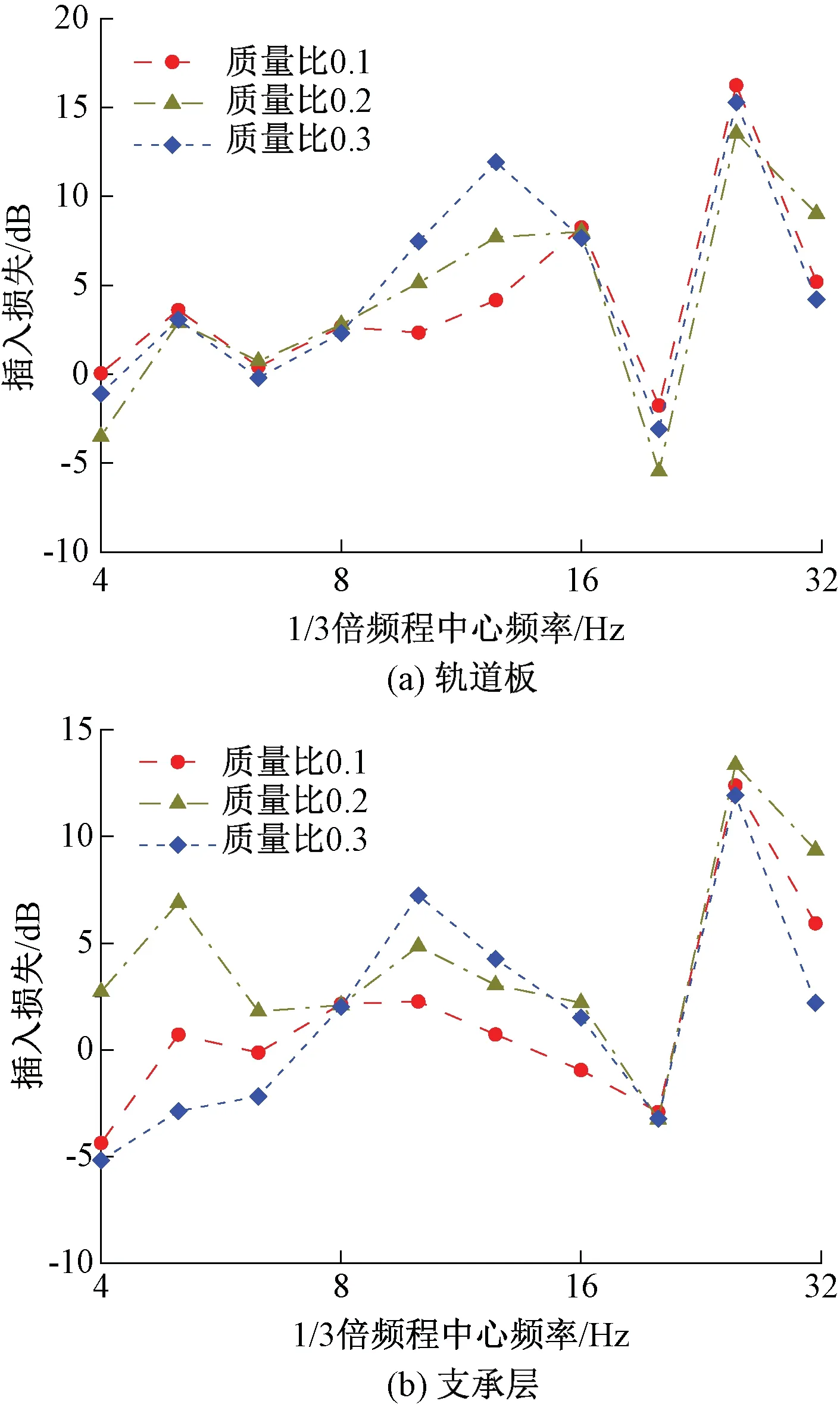
图12 不同工况下轨道板、支承层插入损失

由图11可知，在落轴冲击载荷作用下，无动力吸振器的浮置板分频振级在10 Hz中心频率处出现了较大的峰值，而应用动力吸振器装置后，该中心频率处的振级有所下降，且随着动力吸振器质量比的增加，振级的降幅也会增大；此外，无动力吸振器时浮置板轨道的分频振级在25 Hz中心频率处出现了最大值，而应用动力吸振器后，浮置板轨道在该中心频率处的振级明显降低，表明动力吸振器对浮置板轨道的垂向平动模态以及一阶垂向弯曲模态均有抑制作用。

由图12可知，当频率范围为8～16 Hz及25～32 Hz时，落轴冲击载荷作用下应用动力吸振器浮置板轨道的插入损失均为正值，且在中心频率10 Hz处，插入损失随着动力吸振器质量比的增加而增大，表明应用动力吸振器可对浮置板轨道的低频共振起到良好的抑制作用。在中心频率20 Hz处，轨道板与支承层的插入损失均为负值，说明应用动力吸振器虽然可以抑制浮置板轨道的低频共振，但会在附近频段内出现一定程度的振动放大现象。以应用质量比为0.3的动力吸振器为例，当中心频率为10 Hz时，轨道板、支承层的插入损失分别为7.5、7.2 dB，当中心频率为20 Hz时，轨道板、支承层的插入损失分别为-3.1、-3.2 dB，当中心频率为25 Hz时，轨道板、支承层的插入损失分别为15.3、11.9 dB。

4 结论

针对浮置板轨道低频域振动放大问题，通过设计合理的动力吸振器，并基于落轴冲击试验平台对应用动力吸振器的浮置板轨道进行落轴试验，主要研究了落轴冲击载荷作用下动力吸振器在低频域内对浮置板轨道振动的控制特性。主要结论如下：

(1)浮置板轨道模态仿真结果与测试结果的偏差在±3%以内，且二者的前4阶模态振型保持了一致性，验证了浮置板轨道有限元模型的准确性，保证了动力吸振器设计参数的可靠性。

(2)在落轴冲击载荷下，无动力吸振器的浮置板轨道在10、13、25～30 Hz等频率处会出现较大的峰值；应用不同质量比动力吸振器后，上述频率附近特别是25～30 Hz的频率范围内，轨道板与支承层的振动加速度均明显减小，表明动力吸振器能够有效地抑制浮置板轨道的共振峰值，且动力吸振器质量比越大，控制效果越明显。

(3)在落轴冲击载荷下，浮置板轨道在1/3倍频程中心频率10 Hz处的插入损失为正值，且动力吸振器质量比越大，动力吸振器的振动控制效果越明显；应用质量比为0.3的动力吸振器后，在1/3倍频程中心频率10 Hz处，轨道板、支承层的插入损失分别为7.5、7.2 dB，在中心频率25 Hz处，轨道板、支承层的插入损失分别为15.3、11.9 dB，表明应用动力吸振器的浮置板轨道其低频振动抑制效果明显。