趟车收益与线路总收益之间的关系研究
2021-05-13单杏花文曙东赵冬梅
单杏花,文曙东,赵冬梅
(1.中国铁道科学研究院 电子计算技术研究所,北京 100081;2. 西南交通大学 交通运输与物流学院,四川 成都 610031;3. 西南交通大学 经济管理学院,四川 成都 610031)
单次列车经过多个站点,是典型OD(Origination-Destination)网络收益管理问题[1]。铁路运营方(中国国家铁路集团有限公司(以下简称“国铁集团”)或各铁路局集团有限公司)多数认为单个车次的最优未必导致整个线路的最优,即使目标线路各车次实现收益最大化,也只是该线路其他车次旅客的重新分配,对整条线路来说未必最优,从而对开展列车收益管理持保留态度。也就是说:即便同一线路各车次的客座率达到最优,铁路运营管理人员也不会完全认可,因为对整个线路来说可能不是最优的。这导致了单趟旅客列车收益管理的应用进入了死胡同,做好了或者做不好均很难得到运营管理方的认可。
枢纽式航空公司采用基于OD的网络问题收益管理模型,枢纽式机场和周围小机场形成一个Hub-and-Spoke Network,航空公司的优化目标是网络相关航班整体收益最大。我国铁路客运量大、运输距离长、沿途经过多个站点。一趟车次(子网络)相当于航空公司的一个Hub-and-Spoke Network,而各个路局有若干趟车次,需要辖区线路上(母网络)的所有车次整体收益最优。而国铁集团掌管全国整体铁路,站在国铁集团的立场,还要求整体收益最优,这个网络问题的复杂程度远超航空公司。
航空公司只存在一个Network问题的优化,所以航空公司的航班计划和收益管理独立进行,在确定航班计划后,网络化航班收益管理以相关航班总收益最大为目标,没有母网络和子网络收益最优目标不一致的问题。网络化航空公司在收益管理优化上类似于一趟列车,高速铁路(以下简称“高铁”)网络(区域或全国)的最优化问题在航空领域没有对应的研究对象,如果真要寻找对应的问题,则更相当于站在上帝的视角,探讨全球航空业(包含多个网络化航空公司)最优化问题。困扰铁路运营管理层的问题是“单次列车(子网络)收益最优,整个高铁网(母网络)收益未必最优。”在航空领域,则没有“一个航空公司收益最优,整个航空行业收益未必最优”这样的问题。
因此,与航空不同,在实施高铁客运收益管理之前,理清子网络单次列车收益最优和线路整体最优之间的关系十分重要。母网络总收益和相应子网络收益管理优化目标是否相冲突?是什么因素导致两者优化目标不一致?采取什么样的措施,可以使得母网络整体最优和子网络收益最优目标一致?不捋顺这个关系,将难以推动高铁动态定价和席位控制等收益管理措施的落地实施。
国内外学者已对铁路开行方案(涉及线路总收益)以及收益管理(涉及趟车收益)展开了相关研究。
列车开行方案是列车运输组织计划的核心内容之一,在车辆、编组辆数、列车整备能力、车站通行能力等的限制条件下,确定旅客列车的对数、类别、运行区段和停站,满足旅客出行需求,使铁路企业的线路总收益最大化。国内外诸多学者对其优化方法进行了深入研究,大多数定量研究开行方案编制方法的文献都建立了优化模型。常见的有单目标模型[2-3]、多目标模型[4-5]、双层规划模型[6]等。Kaspi等[7]假设列车无能力约束,以列车旅行时间和旅客旅行时间的综合加权为优化目标,对列车开行方案和列车时刻表综合优化。开行方案的研究基本上是对宏观客流的研究,没有涉及到单次列车收益问题。为了让开行方案更好地满足市场需求,蒲松等[8]研究基于动态客流的高速列车的编制理论与方法,建立实际客流与高铁列车开行方案的反馈调整机制。
基于开行方案编制列车运行图[9],然后做车辆运用计划和乘务组运用计划。这样,在一段时间内,单次列车的停靠站、开行时间和运力就确定了。
接下来,就应该对每趟列车做收益管理,以应付随机变化的市场需求。自20世纪80年代以来,航空公司利用Belobaba[10]的座位期望边际收益(EMSR)模型对座位执行多级价格、座位控制、超售等手段进行管理。随着美国大规模枢纽式机场的发展,机场构建吞吐航班波,顾客可以在短时间内完成转机,美国的大型航空公司进入网络化航空旅客运输模式,网络化的航空公司一般采用基于Network收益管理投标价格模型[11](Bid-Price Model),文献[12-15]对随机线性规划模型(RLP)、概率非线性规划模型(PNLP)和随机动态规划模型(SDP)进行了研究。
李金林等[16]对网络问题存量控制模型和策略进行了探讨,系统介绍了国外学术界存量控制策略,分块预订限制、虚拟嵌套和竞标价格等策略的优劣和适用条件。随后将网络舱位控制的资源分解法与作者提出的单航段超订下舱位控制的R-MDP模型结合,提出超订下网络舱位控制的稳健模型[17]。张秀敏等[18]在国外Network问题研究的基础上,结合国内铁路客运实际,提出网络ODF“隐藏价格”的概念,以EMSR原理解决我国铁路的收益管理优化模型。考虑需求的随机性,单杏花[19]概述了目前铁路采取的共用、复用、通售、限售、模糊/精确预分等手段确保席位可用于多个OD区段,提高客座率。文曙东等[20]还进行了Network问题不同区段全网络嵌套的方案,在列车上各个OD区段,高价值区段的旅客需求可以占用比之价值低的区段的席位,来解决需求随机和固定预分之间的矛盾。近年来,国外收益管理偏向于量化研究顾客选择行为,Gallego等[21]研究显示列车怎样在提供的产品匹配上不同的约束条件,顾客选择行为的Logit嵌套模型。然而,Rusmevichientong等[22]则认为先前有关Logit模型的研究工作都是假定已知旅客选择行为模型参数,而进行市场细分,他考虑管理方并不知道旅客的选择偏好情况下,解决了混合Logit模型的组合优化问题。
上述研究开行方案和趟车收益管理都是独立进行的,蓝伯雄等[23]认为趟车收益最优和整个线路收益最优化是两个分离问题,各自最优结果不一定是统一优化问题的最优结果。在这个前提下,他建立了客运网络开行方案和单次列车收益管理统一模型,首次涉及到开行方案和收益管理收益最优目标统一问题并建立模型加以解决。模型中根据时间段内的需求来确定是否发车,认为时间段内的需求和趟车特征无关,无关旅行时间长短,各个车次的顾客可以完全相互转移,标杆车与普通车次无差别,无法考虑部分顾客买不到心仪车次而改乘其他交通方式的现实情况,也无法解释标杆车爆满而有些车次需求不足的现象。
我国高铁线路网络复杂,如果趟车收益和整个线路收益目标相冲突,那么趟车收益管理的研究意义不大。本文的意义在于解决我国高铁收益管理实施面临的基础性问题——趟车收益管理和线路收益目标是否一致?只有解决了这个问题,才能摆脱铁路管理层“趟车收益做好了,整个线路收益未必最优”的疑虑,从而推动我国高铁列车实施动态定价,科学的席位控制等收益管理措施。
列车收益管理的手段主要是多级票价、存量控制和超售。超售是存量的人为增加,对单车次和整个线路收益关系研究没有影响。本文从多级票价、席位控制两方面入手,来研究单车次和整个线路收益关系。
1 趟车收益和整个线路收益最优之间的冲突因素——多级票价
单次列车进行收益管理时,相应OD上必然执行多级票价,和整个线路收益最优之间会发生冲突。单趟车次执行动态价格时,由于需求对价格的敏感性,其他车次旅客必然会向该趟列车折扣席位转移。该趟列车收益增加了,但整个线路需求并未增加,收益并未达到最优,甚至可能出现总收益下降。本小节考虑执行多级票价时,研究高价值旅客向低票价席位转移对整个网络收益带来的影响。
(1)趟车OD单独执行多级票价引发的问题
假定某条线路上有两列车,定员数量均为600人,只停靠端头两个站。固定票价100元,每天1 000名旅客需求,执行固定票价时,每趟车各自承担500名旅客,客座率均为5/6。执行固定价格时,两个车次客座率和收益见表1。

表1 单级票价100元时下线路各车次收益
如果车次1执行两级票价,并辅以低价票一些退改签和购票时间的限制条件(100、80元),车次2仍执行固定票价,两个车次客座率和收益见表2。

表2 车次1执行两级票价时线路各车次收益
由表2可知,车次1执行两级票价,车次2执行一档固定价格,把车次2的部分旅客吸引到车次1上面,车次1客座率从5/6提高到1,收益从50 000元增加到56 000元。但两趟车的总需求没变,部分全价票旅客向下转移购买了折扣票,导致两趟车总收益下降。单独在某趟列车上执行多级票价,虽然该车次收益增加了,却导致总收益的劣化,趟车收益最优和线路总收益最优发生了冲突。
(2)线路总收益最优化模型
以某条高铁线路为例,每日单向开行N趟列车,把该线路开行的N趟车次合并成一趟站站停靠的虚拟大车A,该大车收益最优,即整体收益最优。各个区段执行固定价格向量pOD,建立虚拟大车收益最优化模型为
(1)

(2)
(3)
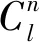
以某个具体的区段od为研究对象,研究该区段执行多级票价是否会给线路总收益带来影响,根据竞争环境设置该od区段的不同票价等级。并在所有能够提供od区段客票的车次上执行,此时od区段的需求应该得到激发有所增加,但高价格的需求会部分转移购买低价格车票,虚拟大车的最优化收益模型为
(4)
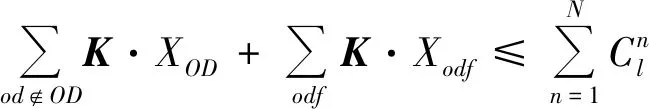
(5)
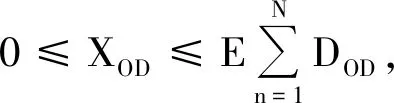
(6)
(7)
式中:Dodf为考虑了多级票价对应的需求;Xodf为odf分配的位置数量;podf为各个odf的价格。
此时,如果所有具备运输od区段旅客的车次上,执行多级票价,最后总的期望收益R2和R1比较:
如果R2>R1,表示od区段执行多级票价时,线路总收益有提高,线路应该在能提供od区段客票的车次上执行多级票价。
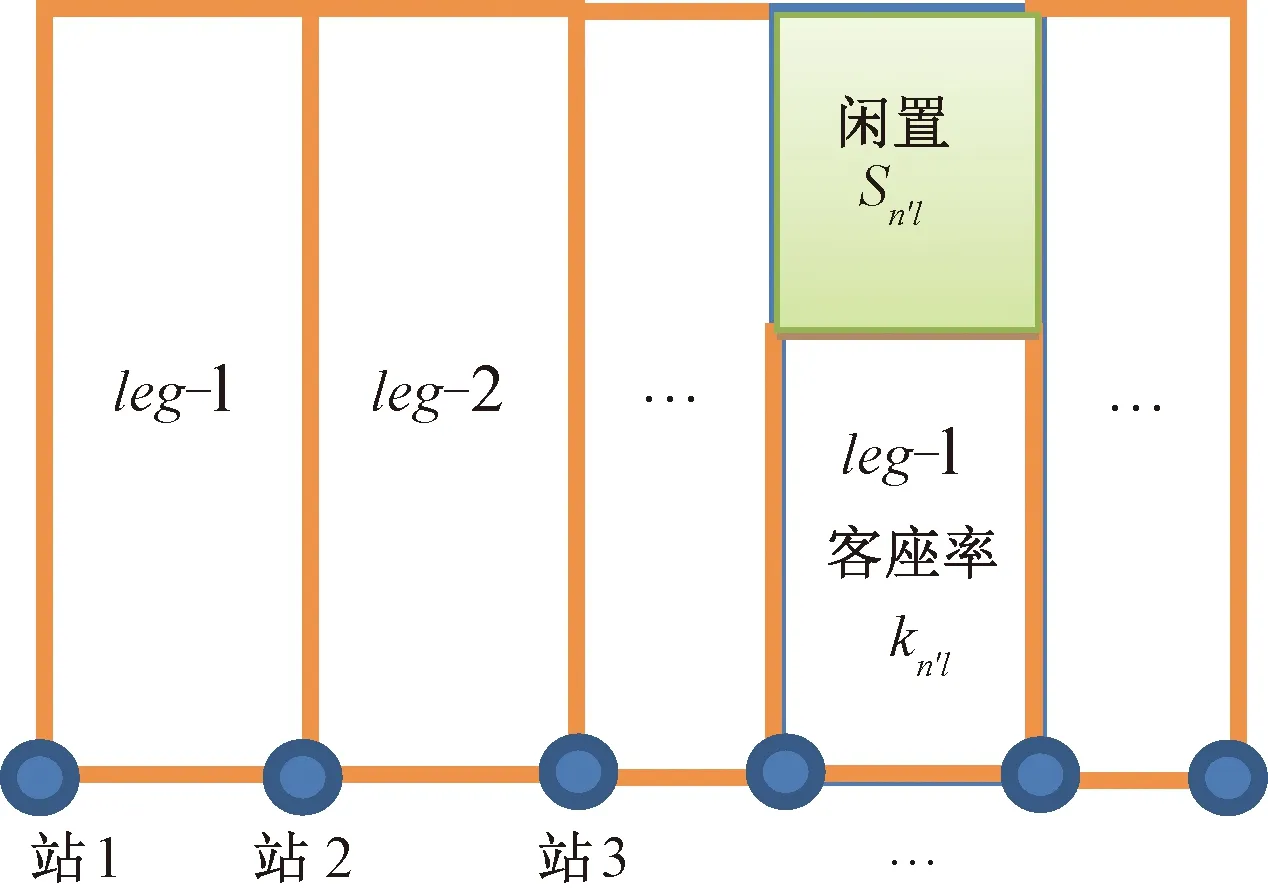
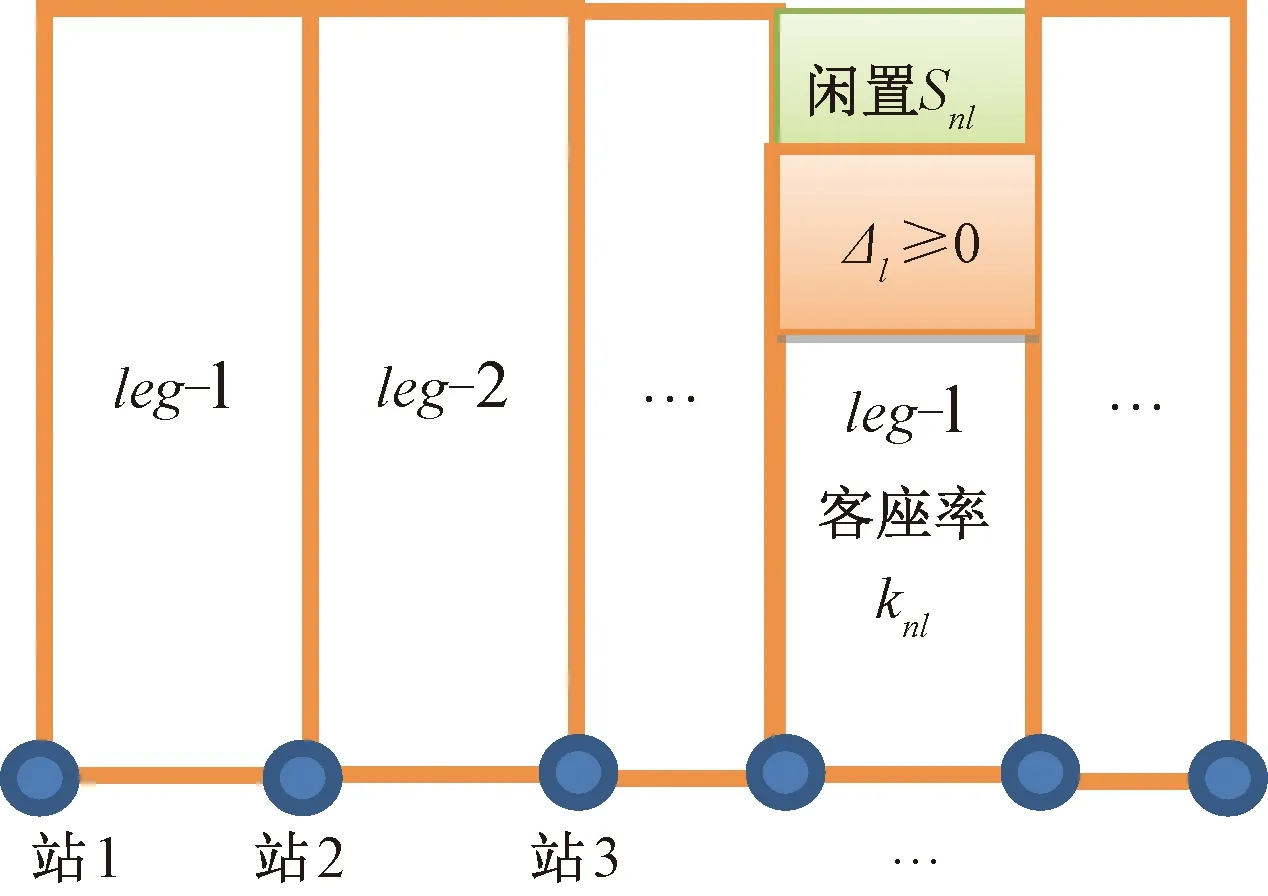
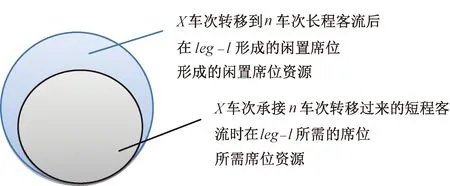
如果果R2 (3)线路OD收益潜力指标 定义:线路OD收益潜力(Revenue Potentiality, RP)指标为γRP=R2/R1,用来度量OD区段收益的潜力。 铁路需要用合适的指标来表征OD执行多级票价时线路收益增加的潜力。细化到线路上每个OD,包含下面3种市场环境: ①该OD区段高铁垄断经营,需求-价格无弹性,降低价格会影响总收益,γRP<1。 ②该OD区段高铁垄断经营,但需求-价格有一定弹性,低票价将激发新的出行需求,执行多级票价线路总收益是否增加未知,不能确定γRP是否大于1。 ③该OD区段高铁和其他运输方式(飞机或大巴)处于竞争状态,需求——价格有很强的弹性,执行多级票价能够提高线路总收益,γRP>1。 显然,γRP越大,需求相对于价格具有弹性,该区段收益越具有潜力。γRP>1时,才考虑该区段执行多级票价。 如果各个铁路局之间为有限市场竞争,不像航空公司那样充分竞争,那么应该由国铁集团统一评估各个OD区段的收益潜力指标γRP,设置全国统一的OD价格体系,有些OD为固定票价,有些OD为多级票价,交由各个铁路局执行。这样,确保了在铁路总收益提高的前提下,各个铁路局开展有序竞争,且能够以一个整体与其他交通方式进行竞争。 如果国铁集团放开管制,让各个铁路局完全自由竞争,允许各个铁路运营企业为实现自身效益最大化制定自己的价格体系,完全不用考虑线路总收益问题,正如民航部门不用考虑各个航空公司效益之和最大化问题一样。 目前,我国高铁执行固定价格,旅客选择车次的行为主要考虑发车时刻和旅行时间长短,各个车次之间不会因为价格的原因相互争抢旅客。影响线路整体收益的因素主要是旅客是否合理的分配到各个车次的席位上去,并达到线路客座率最优的状态。 如果执行多级价格,同样涉及到各个区段不同价格等级的旅客是否能够匹配到合适的列车上。使得各个车次收益最优和线路整体收益最优目标一致。旅客是主动的,只选择对于他来说最合适的车次,不会考虑铁路运营方的意图。在运行图已经确定的条件下,就需要通过存量控制等手段引导旅客去选择合适的车次使得整体线路收益最优,如果趟车席位控制不合理,会引发线路总收益的劣化。 (1)趟车OD席位控制不合理引发的问题 下面举个反例来说明不合理的席位控制,单车次收益和线路整体收益发生冲突。 反例:以武汉—深圳线路为例,有两趟车,见图 1。车次2主要目标是运送武汉—广州和武汉—深圳的顾客。车次1为了收益最优大量发售武汉—广州、深圳方向的旅客,而拒绝长沙—深圳区段的需求,由于剩余的车次2不停靠长沙站,长沙—深圳的需求不能得到满足,引起整体收益的劣化。 图1 趟车席位控制不合理引发总收益劣化例子 通过这个例子可以看出,如果单趟车只顾自身收益最优进行席位控制,那么被拒绝的顾客可能在剩下的车次当中找不到能够乘坐到达目的地,那么这会导致线路总收益的劣化。 (2)趟车收益和线路总收益的相关几个定理 针对一条高铁线路,下面列举并证明几个定理。 定理1:在一个时间段ΔT内,线路通道L上各车次均为每站停靠,乘客乘坐相邻车次的体验一致,被某车次拒绝的顾客可以转乘该时间段内另外一趟列车,那么售票过程中使得每个车次各自达到收益最优,整个线路也收益最优。 证明: 把线路上ΔT时间段的车次组成一趟虚拟大车A,虚拟车次A的最优化收益就是线路的最优化收益,最优化规划模型表达式见(1)~式(3)。 因为买不上目标车次的旅客可以在其他车次进行转移,我们可以把某个列车席位转到另外一个车次,而不影响线路在时间段ΔT的总收益。 对于时间段ΔT内各个车次,建立线性规划模型,车次1的最优化模型 (8) (9) (10) 同样,车次2、3、…、N均可以列出各自收益最优的规划模型,多个车次总收益优化目标函数,是一个标准的多目标规划,设每个车次收益值权重相等为1,对n个车次各自目标函数求和,变形为单目标函数。在这样的假定下,构建在各个车次收益最优基础上的总收益模型: (11) (12) (13) 单独看席位资源约束条件(12),因为每趟列车站站停靠,关联矩阵K值相同,左边超平面完全平行,组成的所有多面体相似。只有两个变量时的最优化模型为 maxf·(X1+X2) (14) 如果f>0,那么上面的最优化结果是f·(C1+C2)。也就是两个变量同时取各自的最大值时,目标函数也达到最大值。这个模型完全等效于 maxf·(X1+X2) (15) s.t.X1+X2≤C1+C2 如果把变量X、C扩展到向量,并且定义向量X≤C时,向量中的任意元素i均有xi≤ci。因为pODF>0,可以把上面1、2、3、…、N个车次收益和的最优化模型中的约束条件式(12)转变为 需求可以在各个车次间转移,所以需求约束条件式(13)可以转换为 (16) 该模型和虚拟车次A的最优化收益模型(8)完全一样,因此,线路上每站停靠的各个车次各自最优收益之和为线路的最大收益。 证明完毕。 定理2:时间段ΔT内,假定线路各个车次停靠站不一样,停靠站少的车次在各个单区段leg上的客座率大于等于同期每站停靠的车次。部分顾客买不到直达车时均愿意中转而不流失,那么在售票过程中使得每个车次各自达到收益最优,整个线路收益也达到最优。 证明:假定时间段ΔT内,线路有1、2、3、…、N个车次,涵盖N-1个leg,合并为一趟虚拟大车T,虚拟大车为每站停靠,如果客观条件没有每站停靠的车次,那么选不上目标车次的旅客可以接受通过中转到达目的地,相当于虚拟大车每站停靠。虚拟大车按照收益最优进行席位分配时,其收益RT最优,整条线路收益RZ也最优。 RZ=RT 现在任选车次n,假定把车次n变为每站停靠的替代车次n′,剩余车次合并成每站停靠的虚拟大车X,这时线路收益为 R=Rn′+RX 根据定理1可以知道,n′和X各自收益最优,整体收益最优。可得 RZ=RT=Rn′+RX 现在选取车次n,非每站停靠。在售票过程中,努力使得n车次收益最优,相比于n′,n车次停靠站少,其他车次上的长程旅客会向车次n转移,被n车次拒绝的短程旅客转向虚拟大车X。假定车次n的竞争力比之前n′提高了,吸引了更多的长程旅客,n′车次各个leg上的客座率均不大于更少停靠站n车的客座率,车次n在单区段l上旅客数量和客座率的变化如下: l上旅客数量增加量为Δl=Sn′l-Snl≥0; l上客座率变化为knl>kn′l。 图2 车次A′每站停靠时leg客座率 图3 车次A各leg客座率 虚拟大车X每站停靠,其长程旅客部分转移到n车次形成了的空闲位置,能够满足n车次转移过来的短程客流,X车leg-l席位资源在旅客转移前后的示意见图4。 图4 虚拟大车X的leg- l席位资源变化示意图 面对按照最优化分配后线路承担的总需求不变的情况下,n′车次减小停靠站数量后,客流在n′和X车次中重新分布,均能满足转移前的客流总需求,总收益不变。所以,车次n和每站停靠的虚拟大车X各自收益最优,整条线路收益也能达到最优。 上面n车次是任意选的一趟列车,和剩余车次组成的虚拟大车X各自收益最优,线路整体收益可达到最优。可以进一步得到,趟车收益最优,线路整体收益也最优。 这里有两个假定进行一下说明。 假定条件1:虚拟大车为每站停靠。如果客观条件没有每站停靠的车次,那么被目标车次拒绝的旅客可以接受通过中转到达目的地,相当于虚拟大车每站停靠。 假定条件2:不是每站停靠的车次,各个leg上的客座率总是大于或等于相同条件下每站停靠的车次。这个假定比较苛刻,但是总的趋势是这个情况。如果这个条件不能满足,意味着该时间段相关长程旅客需求不强烈,需要对运行图进一步优化,多增加该车次的停靠站,增加相应leg上的客座率,从而让该车次能满足该条假定。 证明完毕。 定理3:如果线路各个车次停靠站不一样,但因为运行图设计合理,发售过程中存量控制合理,各个OD区段的顾客不中转,均能买到可以接受的直达车。同样假定停靠站少的车次在各个leg上的客座率大于等于同期每站停靠的车次,那么在售票过程中使得每个车次各自达到收益最优,整个线路收益也达到最优。 证明:因为运行图设计合理,在线路席位资源充足的情况下,各个OD的旅客均能不经过中转乘坐到目的地,整条线路就可以合并成一趟站站停靠的虚拟大车。如同定理2的证明过程。选出任意车次n,用站站停靠的n′替代,余下的车次合并成站站停靠的虚拟车次X。可以证明n和X各自达到最优,其线路总收益最优。 证明完毕。 通过定理1、2、3可以看出,只要运行图的设计能够充分适应旅客需求,或者旅客方便换乘而不感到不方便,各个车次停靠站设置合理,停靠站少的车次各个leg客座率均优于同期站站停的车次。那么在席位控制过程中,各个车次各自努力使得自身收益最优,那么整个线路收益也最优。 图1中的反例就是停靠站设计不合理,长沙—深圳方向的旅客在剩下的车次2上得不到满足,整个线路收益劣化,如果车次2增加了长沙站停靠,满足了长沙-深圳方向的旅客,各个leg上的客座率反而会增加。这样,该车次不能满足定理3中的条件,所以出现趟车收益和整体收益冲突的现象。 本文研究了趟车收益和线路总收益之间的关系,探寻了多级票价和存量控制是引发的收益冲突的根源,就趟车收益和线路总收益目标一致性进行研究。 (1)针对趟车执行多级票价时,引发线路总收益劣化的问题,讨论了国铁集团对各个铁路局的管理模式会制造不同的竞争环境,以及在收益管理执行时应该采取的管制措施。 ①如果国铁集团统一全国高铁作为一个整体参与市场竞争,限制铁路局之间在价格层面上的竞争,那么应该由国铁集团统一评估各个OD区段的收益潜力指标γRP,设置全国统一的OD价格体系,有些OD为固定票价,有些OD为多级票价,交由各个铁路局执行。这样,确保了在铁路总收益提高的前提下,各个铁路局开展有序竞争,且能够以铁路作为一个整体与其他交通方式进行竞争。 ②如果国铁集团放开管制,让各个铁路局完全自主经营,允许各个铁路运营企业为实现自身效益最大化开展价格竞争,那么就应该让各个铁路局自己制定自己的价格体系,完全不用考虑线路总收益的事情,造就完全市场化的环境,正如电信领域、民航领域一样。 (2)针对趟车进行存量控制时,引发线路总收益的劣化问题,从线路所有车次最优化模型入手,证明了合理的开行方案和运行图设计,以及各个车次停靠站合理设置,对于单趟列车只要达到各自收益最优,整条线路总收益也是最优。 可以看出,只要国铁集团执行统一价格体系,运行图的设计能够充分适应旅客需求,或者旅客方便换乘而不感到不方便,那么在售票过程中,各个车次各自努力使得自身收益最优,那么整个线路收益也最优。进一步,各个铁路局充分使得各自担当的列车收益最优,对于铁路整体来说,整条线路收益也能达到最优。 (3)对于开行方案和趟车收益管理的研究关系上,开行方案可以只考虑线路总需求,在运能允许的情况下进行运行图优化,充分满足各个OD的需求,就可以确保趟车收益和线路总收益目标一致性,而不需要建立开行方案和车次收益管理一体化的复杂模型。2 趟车收益和整个线路收益最优之间的冲突因素——席位控制

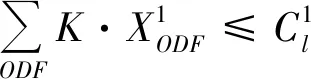
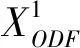
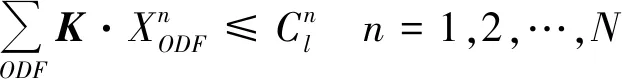
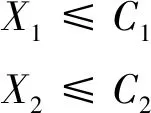
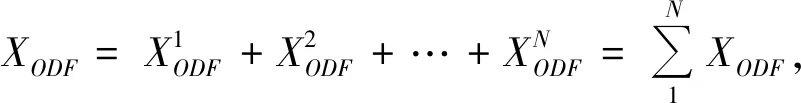
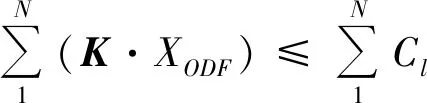
3 结论
