关键审计事项披露个数的市场反应研究
2021-05-12林皓若
林皓若
(暨南大学管理学院,广东 广州 510632)
一、引言
为了改变传统审计报告信息含量不足的缺点,各国近年来陆续施行新审计准则,即在审计报告中增加了披露关键审计事项的要求(IAASB,2015;PCAOB,2017;MOF China,2016)。目前对于关键审计事项的研究主要集中在观察新审计准则的实施是否会对投资者决策、审计师责任以及管理层行为等造成影响,而鲜有关注和分析关键审计事项的具体内容差异可能造成的不同经济后果。本文正是将研究的焦点聚集在关键审计事项的具体披露情况上,基于认知心理学的相关理论提出:对于我国当前的投资者来说,关键审计事项的披露个数将是非常重要的参考指标,关键审计事项披露个数的多少将最终影响投资者在年报公布期间的投资决策,最终引起相应的市场反应。
二、研究假设
具体而言,关键审计事项的披露个数可能从认知心理学中的启发式心理机制对投资者的风险感知以及投资决策产生影响。首先,认知心理学中的代表性启发心理认为人是非理性的决策者,对于决策的判断往往基于其对于决策事项本身或同类事件的以往经验,并使决策者忽略经验样本的代表性以及判断的难易程度(Sloman,1996)。在当前关键审计事项的披露中,由于事项本身涉及的是公司的重大举措、财务报表内容的重大估计与判断和审计师付出的大量审计努力等,因此在具体表述中往往包含“涉及重大的判断”“金额重大”等字眼,这种披露内容在传统的语境中具有强烈的风险色彩,并且审计报告中披露的关键审计事项的个数越多,这些风险导向的词句被提及的频率也越高越密集。因此,在财务报表使用者的专业程度不足以支持其分析关键审计事项的实际意义时,非专业投资者可能基于其较为熟悉的传统语境,认为披露了较多关键审计事项的公司具有较高的风险,从而容易将关键审计事项判断为利空信息。
而在我国,散户也即非专业投资者作为当前投资市场的主体,存在信息接收与识别能力较差的特点,容易受情绪等主观因素影响进行投资决策(陈文博等,2021)。因此,在新审计准则实施的前期,我国市场投资者可能基于关键审计事项带来的风险感知,利用事项披露个数这一最鲜明的指标作为依据纳入投资决策,进而形成特定的市场反应。同时,本文认为在实际的投资活动中,投资者在进行投资的时候不仅关注所投资公司与同期的其他公司业绩上的区别,也会同时关注所投资公司与以前年度业绩的区别,因此我们从横向以及纵向两个维度提出相应的假设。从横向维度而言,当公司在当年的年度报告中披露了越多的关键审计事项时,它就越可能在当年的年报发布日期间遭遇负面的市场反应。而从纵向维度而言,当公司在当年的年度报告中披露了相比上一年度更多/更少的关键审计事项时,它就越可能在当年的年报发布日期间遭遇负面/正面的市场反应。最终,本文的研究假设如下:
H1a:关键审计事项个数的变化与市场反应呈反向相关关系。
H1b:关键审计事项的个数与市场反应呈反向相关关系。
三、研究设计
1.变量定义
(1)被解释变量
本文使用事件研究法研究样本公司在年报公布期间的市场反应,参考以往的文献,本文将被解释变量设置为年报公布前后3天公司的累计超额收益率。其中累计超额收益率是基于市场模型计算得出,事件日期间的正常收益率是使用事件日前30个交易日到前240个交易日,共210天的收益率数据估计得出。
(2)解释变量
本文关注的解释变量有两类:一类为当年审计报告中关键审计事项的披露个数,即Kam_num;另一类为表示与上年度审计报告相比披露的关键审计事项个数增加或者减少的虚拟变量Increase和Decrease,如果增加则Increase为1,否则为0,Decrease同理。
(3)控制变量
为了控制无关变量对市场反应的影响,本文参照李爽等(2001)、廖伟(2009)和周红(2004)等的做法,选取了公司规模(Size)、资产负债率(Lev)、营业收入增长率(Growth)、净资产收益率(ROE)以及分析师预测偏差(FERROR)作为模型的控制变量,并对审计意见类型进行了控制。
3.模型设计
最终,本文的横向维度模型构建如下:
CARi=α1Kam_num+β1FERRORi+β2Sizei+β3LEVi+β4Growthi+β5ROEi+εi
纵向维度模型构建如下:
CARi=α1INCREASEi+α2DECREASEi+β1FERRORi+β2Sizei+β3LEVi+β4Growthi+β5ROEi+εi
3.样本选择与数据来源
由于新审计准则从2017年1月1日仅对部分A+H股公司实施,2018年1月1日对所有上市公司实施,而本文研究的是上市公司的关键审计事项个数及个数的后续变化的市场经济后果,因此本文将样本选取为2018年~2019年披露了关键审计事项的A股上市公司,并将样本做了以下处理:(1)剔除了金融保险行业的样本公司;(2)剔除了事件日前后15天发生过其他公司事件公告的样本公司;(3)剔除了审计数据以及财务数据缺失的样本公司;(4)剔除了ST类样本公司。经过筛选,本文最终得到5233个样本观察值。本文中关键审计事项的数据来源于中国研究数据服务平台(CNRDS)数据库,财务与审计数据则来源于国泰安数据库。
四、实证结果分析
1.描述性统计
在经过前述流程的样本筛选过程之后,市场反应回归模型的最终样本为5233个观测值。样本的描述统计情况见表1。

表1 回归模型总体样本描述统计表
从描述统计的结果可以看出在不同公司之间,累计超额收益率CAR的相差较大,在年报发布日前后[-3,3]的窗口区间里,累计超额收益率CAR最小的公司为-0.315,而CAR最大的公司则可达到0.575,而就样本总体而言,CAR均值接近于0。而对于关键审计事项的个数,可以看出在公司披露的关键审计事项个数最少为1,最多为6,但大部分公司披露的事项个数在2个左右;而在前后年份间,选择增加或者减少关键审计事项披露个数的公司都较少,分别占据了样本总体的10%左右,这也与以往文献发现的事项变动情况相一致。
2.均值T检验
(1)日平均超额收益率及累计平均超额收益率分析
为了验证公司的关键审计事项披露个数变化是否能够对当年年报公布的市场反应造成影响,我们分别对增加及减少了关键审计事项披露个数的两个样本组的日平均超额收益率AAR以及累计平均超额收益率CAAR分别进行了分析。
以增加了关键审计事项个数的样本组为基础,我们计算得出该样本组在审计报告公布日前后10个交易日的日平均超额收益率AAR及其累计平均超额收益率CAAR。AAR与CAAR的变化情况如图1所示。

图1 增加关键审计事项披露个数样本组的AAR与CAAR
从图1所示曲线可以看出增加了关键审计事项个数的样本组公司在事件日前后的AAR与CAAR变化趋势发生了较大改变。在[-10,-5]区间,样本组公司的AAR和CAAR基本在0左右随机地波动。而在[-5,5]区间,样本组公司的AAR发生了快速且大幅的下跌,而这期间CAAR的值也开始显著地小于0,这种下跌的态势直到第5日才最终结束,随后在[5,10]的区间里,AAR开始恢复到正常的水平,与之相对应的CAAR也开始出现回升。增加了关键审计事项个数的样本组公司的AAR及CAAR变动情况表明,市场对于增加了关键审计事项个数的审计报告作出了一定程度的负面反应,这种反应在年报发布日前便开始出现,并将持续到年报发布日后的一段时间。
同理,我们可以得到另一样本组的变化情况如图2所示。
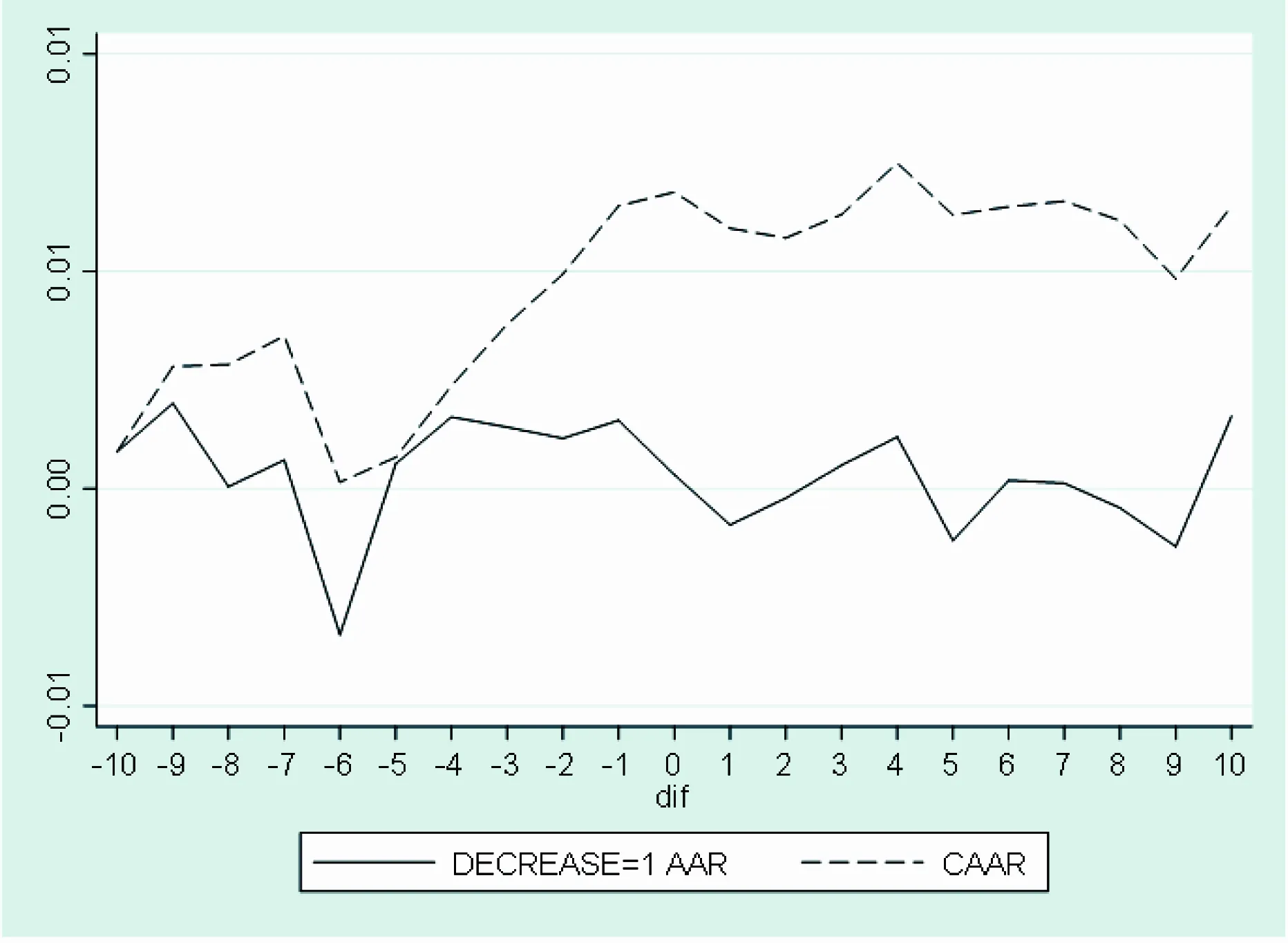
图2 减少关键审计事项披露个数样本组的AAR与CAAR
从图2所示曲线可以看出,减少了关键审计事项披露个数的样本组公司在事件日前后的AAR与CAAR变化趋势同样发生了改变。在[-10,-5]区间,样本组公司的AAR和CAAR同样在0左右随机地波动。而在[-5,0]区间,样本组公司的AAR开始出现连续且正向的市场反应,CAAR开始稳定地上升,但这种变化的态势并没有持续太久,随后在[0,10]的区间里,减少了关键审计事项披露个数的样本组公司的AAR已经开始恢复到正常的水平,与之相对应的CAAR也重现进入随机波动的状态。
(2)累计超额收益率分析
为了进一步研究两个样本组公司在事件期窗口内的AAR变化是否最终导致了事件期内样本组公司的累计超额收益率发生了显著变化,我们对两个样本组公司在事件日前后不同的时间窗口内的累计超额收益率进行了是否为0的均值T检验,结果如表2所示。

表2 不同时间窗口区间内CAR(-t,t)的T检验
如表2所示,一方面,增加了关键审计事项披露个数的样本组公司在[-10,10]到[-1,1]等不同的时间窗口区间内累计超额收益率都显著地小于0,这说明从总体来看,市场对增加了关键审计事项披露个数的审计报告发布产生了负面的市场反应。另一方面,减少了关键审计事项披露个数的样本组公司在[-10,10]到[-2,2]的区间内累计超额收益率都显著地大于0,只有在[-1,1]区间的累计超额收益率CAR不显著,说明市场对减少关键审计事项披露个数的审计报告发布产生了正面的市场反应,但市场发生反应的时间可能不在事件日当天。总的来说,对两个样本组时间窗口区间内的累计超额收益率CAR的检验结果支持了我们的研究假设。
3.多元回归分析
对样本公司进行的均值t检验可以在一定程度上反映关键审计事项披露个数的变动所造成的市场反应的不同,但无法排除其他影响因素的干扰,同时均值t检验也不适用于研究横向维度下关键审计事项个数不同所造成的市场反应差异。因此,为了尽可能排除无关影响因素对研究结果的干扰,本文采取多元回归的方式进行进一步的研究。
对于纵向维度分析,我们使用如下的回归模型:
CARi=α1INCREASEi+α2DECREASEi+β1FERRORi+β2Sizei+β3LEVi+β4Growthi+β5ROEi+εi
回归分析的结果如表3所示。
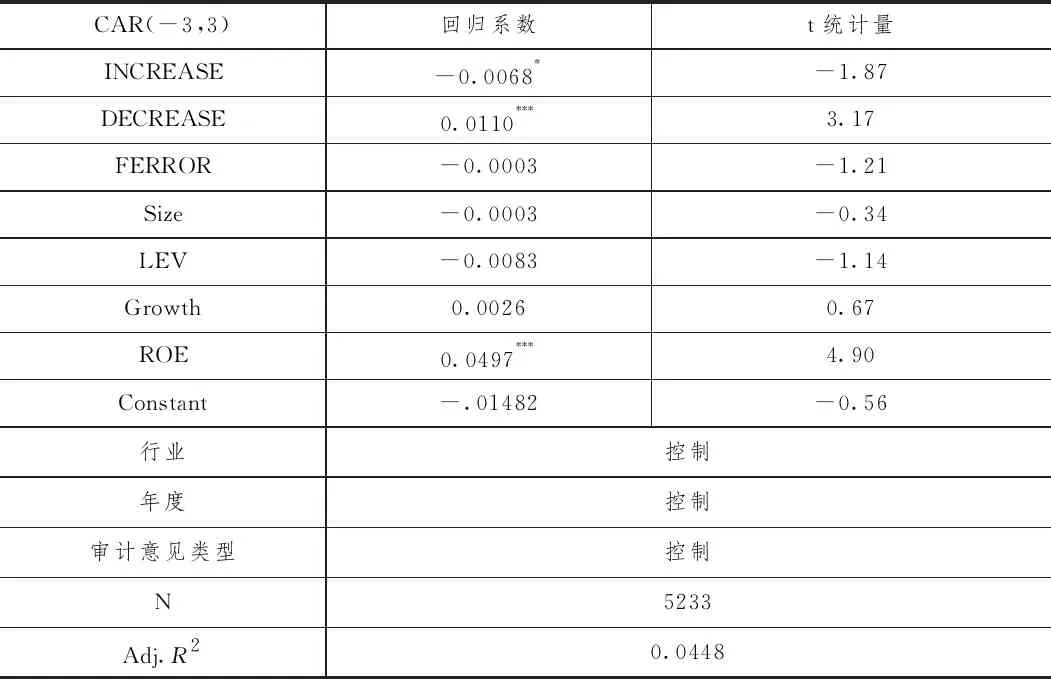
表3 市场模型纵向维度——多元回归分析结果
多元回归分析的结果显示,变量INCREASE的回归系数为-0.0068,在10%的水平上显著为负,表明在控制了其他变量的情况下,公司在当年年度报告中相比上年增加披露关键审计事项时,公司在年报发布日期间的市场反应就越负面。而变量DECREASE的回归系数为0.0110,在1%的水平上显著为正,这意味着在控制了其他变量的情况下,公司在当年年度报告中相比上年减少披露关键审计事项时,公司在年报发布日期间的市场反应就越积极。
对于横向维度的分析,我们使用以下的回归模型:
CARi=α1Kam_num+β1FERRORi+β2Sizei+β3LEVi+β4Growthi+β5ROEi+εi
回归分析的结果如表4所示。
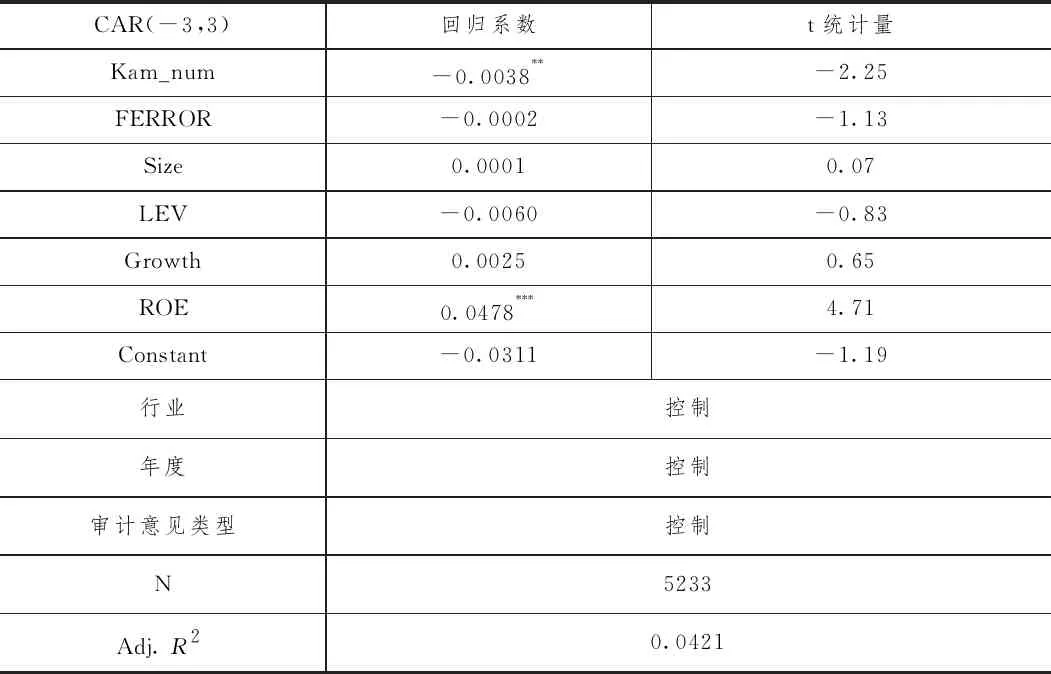
表4 市场模型横向维度——多元回归分析结果
从横向维度的多元回归分析结果看,Kam_num的系数显著为负,意味着在控制了其他变量的情况下,在当年的年度报告中披露更多关键审计事项的公司,在年报发布日期间的市场反应更负面。
五、稳健性分析
1.调整事件窗口的市场反应结果
为了考察上述结论的可靠性与稳健性,更为全面准确地研究证券市场对公司的审计报告中披露关键审计事项个数的市场反应,本文将在这一部分将回归模型中累计超额收益率CAR计算的时间窗口区间从原来的[-3,3]调整为[-5,5]进行分析。
使用调整后的累计超额收益率CAR重复之前的多元回归分析,我们得到稳健性分析的结果如表5所示。
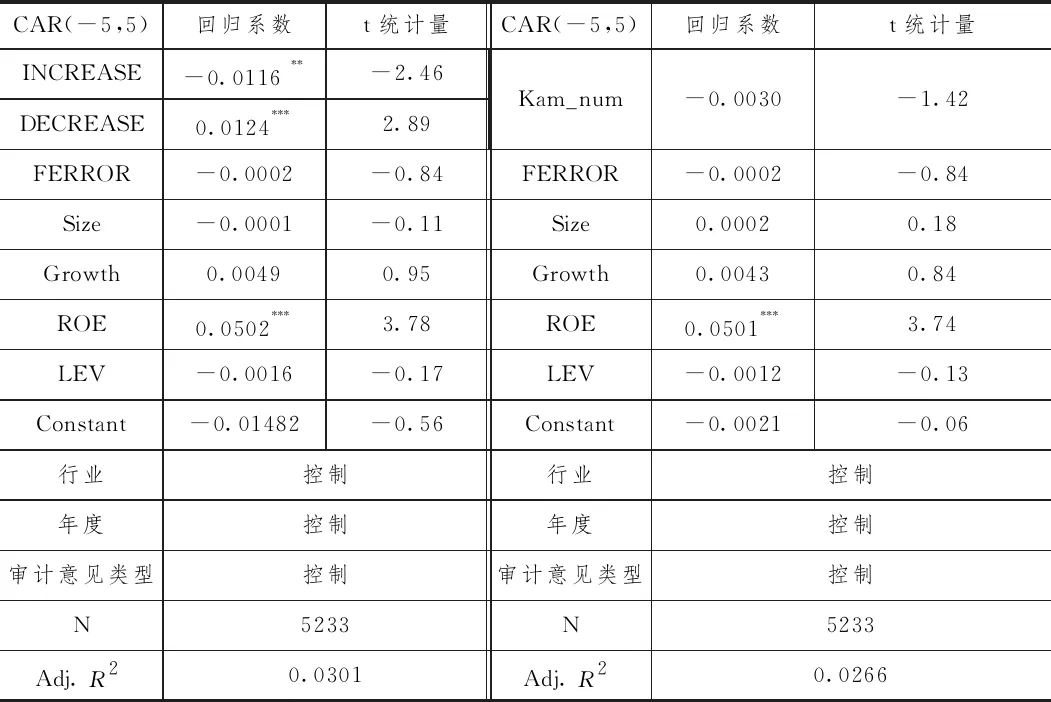
表5 纵向与横向维度多元回归分析结果
以上为使用调整后的累计超额收益率CAR进行多元回归分析得出的结果。表格内容左侧是对纵向维度的分析结果,右侧是对横向维度的分析结果。
对稳健性结果的分析与主回归分析一致,此处不再赘述。可以看到,本文的主要变量在稳健性分析结果中均未发生显著变化,本文的主要分析结果依旧是稳健的。
2.调整超额收益率计算方法的市场反应结果
为了避免市场模型计算超额收益率的过程中无关因素对研究结果造成的干扰,本文在这一部分调整了超额收益率的计算方法,使用市场调整模型重复主要的检验,以确保原结果的稳健性。
我们以[-3,3]为事件窗口期,使用市场调整模型计算得出累计超额收益率CAR,并将其替换到原有的模型中进行多元回归分析。分析结果如表6所示。
稳健性分析的结果表明,在改用另一种常用的超额收益计算方法也即市场调整模型法计算本文的因变量累计超额收益率,并重复主要的分析检验后,得到的研究结果与原有的研究结果没有显著差异,因此原有的研究结果依旧是稳健的。
表6 市场调整模型——纵向与横向维度多元回归分析结果

CAR(-3,3)回归系数t统计量CAR(-3,3)回归系数t统计量INCREASE-0.0074-2.13DECREASE0.01073.16Kam_num-0.0039-2.34FERROR-0.0004-2.03FERROR-0.0004-1.96Size-0.0003-0.30Size0.00010.14Growth0.00641.72Growth0.00641.70ROE0.07057.10ROE0.06876.90LEV-0.0054-0.76LEV-0.0046-0.65Constant-0.0384-1.52Constant-0.0375-1.47行业控制行业控制年度控制年度控制审计意见类型控制审计意见类型控制N5233N5233Adj.R20.0518Adj.R20.0491
六、研究结论
本文研究了关键审计事项个数的市场反应,以 2018年~2019年披露了关键审计事项的上市公司作为样本,通过事件研究法研究了上市公司在年报中关键审计事项披露个数以及相较上年的个数变化会否对当年年报发布期间公司的市场反应造成影响,并发现在年报中增加/减少关键审计事项披露的个数的上市公司以及在年报中披露更多关键审计事项的上市公司,会在当年的年报发布期间相对于其他公司遭遇更加消极/积极的市场反应,这表明投资者在关注关键审计事项的同时可能将关键审计事项的个数视为衡量公司风险的一种指标,从而当报告中关键审计事项个数越多,投资者越可能减少对公司的投资,最终在关键审计事项个数与市场反应间形成负向相关关系。本文在关键审计事项披露的市场反应研究的基础上,提出关键审计事项的披露个数会进一步影响其年报公布期间的市场反应,丰富了关键审计事项的相关文献,既有助于注册会计师更多地了解关键审计事项的披露后果。也有助于帮助监管部门更好地推行新审计准则。
